尾气温差发电系统建模及影响规律分析

2024-03-21马宗正

机械科学与技术 2024年2期

马宗正

（河南工程学院机械工程学院，郑州 451191）

温差发电的前提是温差发电器两端有温差，也即温差发电器需要冷源和热源[1-2]。已有的研究表明，不论是发动机尾气还是冷却液，都是较为理想的热源[3-4]，通过水冷[5-6]、强制风冷[7]或者自然冷却[8]方式提供冷源，即可利用温差发电技术对发动机能量进行回收利用[9]。

Hatzikraniotis 等开发的针对尾气能量回收的温差发电系统，冷却采用156 片20mm 高的散热片，依靠自然风冷却，在车速为90 km/h 和120 km/h 的情况下，温差发电模块的热端温度不超过225 ℃，当环境温度为20 ℃时冷端温度不超过80 ℃，此种温差发电器的转换效率在2.5%～3.2% 之间[10]；Wang 等对风冷散热尾气能量回收装置采用数值计算的方法进行了改进，通过数值分析可知，散热片长度减少而增加边缘面积能够有效增加温差发电能量密度，根据其比对结果，在采用改进形式的散热片后，即使散热效率降低20.93%的情况下温差发电模块的能量密度可增加到88.7%[11]；Orr 等利用热管技术设计的尾气能量回收装置，转换效率能够达到2.46%，燃油消耗量能够降低1.57%[12]；Massaguer 等的研究结果表明，把温差发电装置安装到1.4 L 的汽油发动机上，最大输出电能可达到111 W[13]；Lobufets 等的研究结果表明，当发动机转速为2 000 r/min、平均有效压力为0.6 MPa 时，最大输出功率可达119 W，最大的能量转换效率可达2.8%[8]；Kobayashi 等利用SiGe 温差发电模块在3 L 汽油机上的试验结果表明，当利用排气管作为热源直接与温差发电模块的热端相连、另一端利用水冷的方式，在汽车车速为60 km/h 时，单片温差发电模块的最大输出功率为1.2 W[14]；Nyambayar 等设计新型温差发电装置用于回收冷却系统能量，研究结果表明，采用其设计的温差发电装置、模拟车速为80 km/h 时，能量回收效率为3.2%，而在怠速时能量回收效率可达10%[15]。

以上研究表明，基于温差发电对发动机尾气的废弃能量进行回收利用能够提高发动机热效率，但是大多数研究是基于实验台架，从能量传递的角度来分析其输出能量的研究较少，为此从能量传递的角度对其进行分析，进而得到其输出能量的计算方法。

1 尾气温差发电系统简介

基于温差发电技术的发动机尾气能量回收系统如图1 所示，温差发电器串联到排气系统中，一般位于三元催化器之后（主要考虑温差发电模块的耐高温程度，一般的温差发电模块电量输出电源线是利用焊锡焊接的，因此高温承受能力不高），温差发电器一般为三明治结构，如图2 所示，由能量收集器（集热器）、温差发电器模块和散热器组成，其中能量收集器用于收集热量，作为温差发电的能量获取端，散热器用于形成温差发电器能量散失端，温差发电模块是半导体模块，通过自身的塞贝克效应将热量转化为电能。

图1 温差发电系统示意图Fig.1 Schematic diagram of the TEG system

图2 温差发电装置示意图Fig.2 Schematic diagram of the TEG system

2 温差发电系统能量计算

从能量传递的角度单独把温差发电器做一个简化，可以看作能量从尾气中传递给温差发电器，部分能量以电能的形式输出，部分能量以热量散失的形式进入周围的环境，其示意图见图3。

从热端吸收的热量和冷端散失的热量可表示为：

同时根据传热过程，还可以表达为另外一种方式：

由式（1）和（3）可得

由式（2）和式（4）可得

根据温差发电片输出电能的情况，可得

热端面和冷端面采用的导热材料均为铜片，同时热侧需要与发动机尾气进行对流换热，故热侧的热阻可表示为

式中：Ka为金属壳体的热阻值，Ω，Ka=L/（μS），μ为导热系数，W/（m·℃），L为厚度，m，S为面积，m2；hf为对流换热系数，W/（m2·℃）。

hf的确定需要根据流体的性质，即是层流还是湍流，因此首先根据雷诺数确定是层流还是湍流，如果雷诺数大于2 300 就是湍流，小于就是层流，雷诺系数Re的计算公式为

式中：u为介质平均流速，m/s；de为管道直径，m，如果是矩形管，采用当量直径，则，f为流通截面积，m2，U为湿润周长，m。

如果是层流，对流换热系数hf为

式中：Nu为努谢尔数，层流为4.36； λ为流体的导热系数，W/（m2·K）。

如果是湍流，对流换热系数hf为

式中：n为普朗特常数系数，加热取0.4，散热取0.3；Pr为普朗特数，µ1为运动黏度，m2/s ；Cp为等比热容，J/K。

对于温差发电系统来说，N、 αTEG、TA、TS、KTEG、Rload、Ksink、Ka都是已知量，式（9）～式（11）中未知参数只有TH、TC、I这3 个变量，但由于这3 个方程是非线性方程，很难得到解析解，因此可以采用MATLAB 中的fsolve 函数得到数值解。在求解过程中，迭代初始值x0=[250;200;0.2]，迭代次数采用默认值（5 600 步）即可得到相关数值解，具体调用如下：[x,fval] =fsolve（@（x） myfun（x,Ki（i））,x0），其中myfun 为式（9）～式（11）自定义计算函数。

3 实验验证

为了验证上述计算方法的正确性，采用台架的方法进行了验证，台架基于EQ491 型发动机（具体参数见表1），辅助以测功机（电涡流），在试验之前加工完成温差发电器，并串入排气系统中，见图1。

表1 EQ491 型发动机参数Tab.1 Parameters of the EQ491 engine

验证试验需要测试冷端和热端温度、输出电流等，为此需要增加温度测量和电流测量设备。本次试验温差采用热电偶测量，电流采用万用表测量，具体设备参数及精度见表2 和表3。

表3 仪器测量范围及精度Tab.3 Measurement and accuracy of the equipment

通过调整外部负载阻值进行了计算结果的验证，如图4 所示。由图4 可知，仿真结果与实验结果趋势基本吻合，且输出功率的差距在5%以内，可以认为上述计算方法能够用于温差发电系统的计算。

图4 温差发电器仿真与实验结果对比Fig.4 Comparison of simulation and experiment results

4 温差发电器输出功率影响因素分析

在验证计算方法可行的基础上，对影响温差发电器工作性能的因素进行了分析。

4.1 外部负载对输出功率的影响

如图5 所示为外部负载对输出功率的影响规律(N=100，Ksink=0.84，Ta=475.15，Ki=1/0.039 96，TS=296，aTEG=0.05，KTEG=0.659)。由图5 可知，随着外部负载的增加，输出功率呈现先增加后下降的趋势，在外部负载为250 Ω 时温差发电器输出功率达到最大值38 W，之后随着外部负载的增加功率下降。

图5 外部负载对输出功率的影响Fig.5 Effect of external load on output power

这与一般蓄电池不同，一般蓄电池是当外部负载与内阻值一致时输出功率达到最大值，由式（9）和式（10）可知温差发电模块的内阻值会对其两端的温差产生影响，如图6 所示为外部负载变化时温差发电模块两端温度及温差的变化，可见当外部负载增加时热端温度变大，冷端温度变小，从而使得温差变大，根据公式可知，当温差和负载同时变化时，其变化规律就会变得复杂，而输出功率最大值也不和一般蓄电池一样容易预测。但是在实际应用中如果能够控制温差发电模块两端的温差保持不变，则其变化规律和一般蓄电池一致，比如当设定两端温差为30 K，随着外部负载的变化规律如图7 所示，可见此时温差发电模块的最大功率点在150 Ω 处。

图6 外部负载变化时温度及温差的变化Fig.6 Vibration of temperature during the change of external load

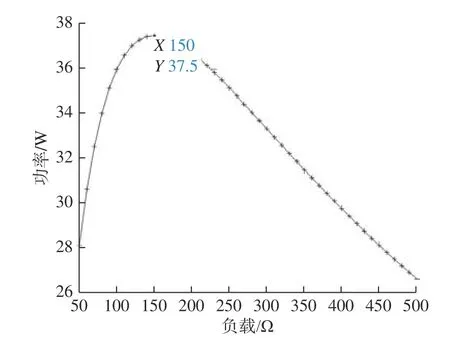
图7 温差一定时输出功率随外部负载的变化Fig.7 Effect of external load on output power at fixed temperature difference

4.2 塞贝克系数的影响

如图8 所示为塞贝克系数对输出功率的影响(N=100，Ksink=0.84，Ta=475.15，Ki=1/0.039 96，TS=296，KTEG=0.659，RTEG=1.5，Rload=250)。由图8 可知，随着塞贝克系数的增加，温差发电器的输出功率呈现先增加后降低的趋势，最大功率为51 W，此时对应的塞贝克系数为0.09。

图8 塞贝克系数对输出功率的影响Fig.8 Effect of see-beck coefficient on output power

一般认为，塞贝克系数越大输出功率越大，此时的分析结果与此不符。主要原因在于塞贝克系数影响传热过程（见式(3)与式(4)），当塞贝克系数变化时两端的温度也在发生变化，具体变化可见图9，由图9 可知，当塞贝克系数增加时两端的温差不断变小，此时虽然塞贝克系数增加了，但是由于两端温差变小，输出功率反而会变小。

图9 塞贝克系数变化时温度及温差的变化Fig.9 Vibration of temperature during the see-beck coefficient change

但同时也会发现，温差发电器的塞贝克系数一般为 0.05 左右，此时提升塞贝克系数是会显著提升输出功率。

4.3 温差发电模块内阻值的影响

如图10 所示为温差发电模块内阻值对输出功率的影响(N=100，Ksink=0.84，TA=475.15，Ki=1/0.039 96，TS=296，KTEG=0.659，Rload=250，aTEG=0.05)。

图10 温差发电模块内阻值对输出功率的影响Fig.10 Effect of inner resistance of TEG system on output power

由图10 可知，温差发电模块内阻值为0 时输出功率最大（内阻实际不可能为0）；当温差发电模块内阻值增加时，温差发电模块输出功率呈下降趋势，在内阻值为0.9 Ω 时输出功率已经下降到28 W。

图11 温差发电模块电流随内阻值变化Fig.11 Vibration of current with the change of inner resistance

可见，为了能够提高温差发电模块输出功率，降低其内阻值是一个选择，但是会受到相关制造工艺的影响。

4.4 温差发电模块导热系数的影响

如图12 所示为温差发电模块导热系数对输出功率的影响(N=100，Ksink=0.84，TA=475.15，Rload=50，Ki=1/0.039 96，TS=296，RTEG=1.5，aTEG=0.05)。

图12 温差发电模块导热系数对输出功率的影响Fig.12 Effect of inner resistance on output power

由图12 可知，当导热系数变大后，温差发电模块的输出功率降低，当导热系数从0.01 升高到0.9 时，输出功率从354 W 降低到了69 W，下降幅度为80%，（原输出功率-下降后输出功率）/原输出功率，可见导热系数的变化对于温差发电输出功率影响较大。

温差发电模块主要材料为半导体材料，其本身具有一定的导热系数，但是导热系数数值较小，从温差发电的角度来说，希望是绝热材料，这样两端的能量传递较少，能够最大程度的输出电能，因此需要尽量减少温差发电模块的导热系数。

4.5 热端、冷端散热系数的影响

为了对比热端散热系数对温差发电模块输出功率的影响，在其他参数保持不变的情况下，调整散热系数从10～50，考察输出功率的变化情况，如图13所示为热端散热系数变化时温差发电模块输出功率的变化(N=100，Ksink=0.84，TA=475.15，Rload=50，TS=296，RTEG=1.5，aTEG=0.05)。

图13 热端散热系数变化时温差发电模块输出功率的变化Fig.13 Effect of heat dissipation coefficient of hot end on output power

可见，当散热系数由10 变到50 时，输出功率从10 W 增加到82 W，此时增加幅度为720%，可见，提升热端散热系数能够显著提升温差发电模块输出功率。

热端散热系数的提升能够增加热端获取能量的能力，QH=Ki(TA-TH)，因此在实际应用中提升热端散热系数可提高输出功率。

同时为了对比，对热端散热器采用不同散热系数的散热器（分别为20，30 和40）进行了试验，相关试验结果见图13，该试验能够进一步验证计算模型的可行性。

与此同时也考察了冷端系数变化时输出功率的变化功率，如图14 所示。其他参数为：N=100，TA=475.15，Rload=50，Ki=1/0.039 96，TS=296，RTEG=1.5，aTEG=0.05。由图14 可知，当冷端散热系数增加时输出功率也会提升当散热系数由0 变到1 时，输出功率从0 增加到40 W。