采用轮轨振动加速度信号对车轮扁疤的识别研究

杨丽蓉，和振兴，王开云 , ，刘旭麒，曹子勇

（1.兰州交通大学 机电工程学院，兰州 730070；2.西南交通大学 牵引动力国家重点实验室，成都 610031）

车轮扁疤将恶化列车运行的动力学性能[1]，因此能有效识别将车轮扁疤有效识别，对确保行车的稳定性和和安全性十分必要。目前，国内外学者对车轮扁疤的动力学影响开展了大量研究。研究发现车轮扁疤所引起的轮轨之间的冲击振动可产生高于正常轮载3 ～ 4 倍的高频轮轨冲击力[2]，在扁疤冲击下车轮会出现多次跳轨现象[3]，对车辆-轨道系统都会产生严重的影响。杨逸凡等[4]详细分析了实测和拟合擦伤激扰下的轮轨动态响应特征，车轮扁疤对轨道、扣件弹条和轨下垫层等结构振动影响较大。

对车轮扁疤的识别理论研究日益重视，目前主要研究通过轮对、转向架或车体振动来识别扁疤冲击。考虑到车轮扁疤对高速列车轮对的影响，杨光等[5]将车轮扁疤损伤考虑为车轮轮径变化，研究得到了不同速度等级下车轮扁疤长度安全限值。REN 等[6]建立三维车轮扁疤模型，得出车轮扁疤的安全允许长度最大为25 mm。Chen 等[7]采用基于高分辨率ACMD 的时间频率分析方法，来实现对扁疤故障检测。Shim 等[8]对振动信号应用频谱分析方法结合阶数分析来实现对车轮扁疤的检测。Zhou等[9]通过分析电信号来识别车轮扁疤或其他旋转部件缺陷的存在。Shi 等[10]采用车体加速度来识别车轮扁疤，发现信噪比远低于轴箱加速度水平，因此采用车体加速度不足以识别车轮扁疤。Bernal 等[11]使用基于包络功率谱分析、波峰因数等指标检测车轮扁疤，结果表明，基于转向架和车身无法有效识别车轮扁疤。

从上述研究可以看出，通过车轮、轴箱响应识别扁疤，信号的信噪比高，理论上识别效果较好，但需在每个车轮上安装传感器随车实时运行，传感器的安装数量、质量要求以及维护成本较高。

因此本文采用车辆-轨道耦合动力学理论及小波包分解方法，通过研究车轮扁疤与车辆系统和轨道系统的动力学响应，确定通过钢轨振动识别车轮扁疤的能力最好。

1 车辆-轨道耦合动力学模型

以CRH380B 型高速车为例，将车辆视为以恒定速度运行于轨道上的多刚体系统，包括一个车体、两个构架及4 个轮对共7 个刚体，每个刚体有5 个方向自由度，二系悬挂系统连接车体及构架，而构架与轮对之间连接由一系悬挂系统提供，因此每节车考虑35 个自由度[1]。如图1 所示，其中Kpz为一系与二系悬挂刚度，Cpz为一系与二系悬挂阻尼。Pi(t)为单侧车轮的轮轨垂向作用力（i=14），4 个轮对处的钢轨不平顺为Z0i（i=1 ～ 4）[12]。

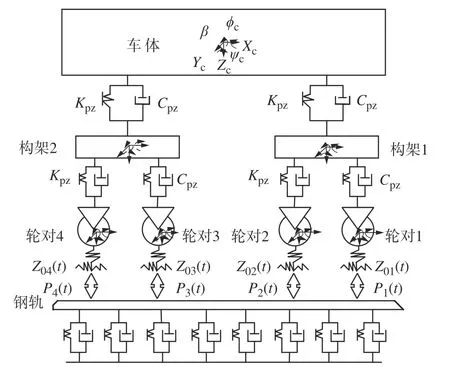
图1 车辆-轨道耦合动力学模型Fig.1 Vehicle-track coupling dynamics model

对于轨道模型，以双块式无砟轨道为例，将钢轨视为连续弹性离散点支承上的无限长梁，钢轨扣件固定在轨道板支承结构上并提供一定弹性，模型中忽略钢筋混凝土整体道床的变形影响[13]。车辆和轨道之间的耦合关系通过轮轨空间接触模型实现[1]。

高速列车运行过程中，在出现列车制动或非正常车轮抱死的时候，车轮与钢轨之间摩擦类型发生转变，会致使车轮踏面损伤而形成扁疤[14]。如图2所示，在高速行车状态下，车轮滚至图2a）中A点后，会脱离其钢轨表面，进而在旋转的同时向前作惯性运动，最终向下跌落，在B点处接触轨面，而冲击在轨面上[1]。

图2 高速时扁疤车轮运动示意图Fig.2 Motion of flat wheel at high speed

2 扁疤损伤的小波包能量指标定义

2.1 小波包变换

小波包定理详细叙述[15]如下，在f(·-k)|k∈z构成规范正交基时且：

则{F(·-2k);k∈z} 是E=span{f(·-n);n∈Z}的规范正交基。

当f是尺度函数 ϕ时，尺度函数 ϕ 与 小波 ψ的二尺度关系为：

将上述公式应用于Wj空间，生成小波包子空间，其一般迭代公式为：

假设某振动信号f(t)经过小波包的j层分解，每个分解信号x(t)可表达为

其中

定义cij.k为小波包系数，表达式为

与小波变换所不同的是小波包分解对每一层分解得到的系数都要进行再分解，而不像小波分解那样只有低频系数会再分解。如图3 所示，分解时首先将信号分解成低频L1和高频H1，在该过程中两个信号各占一半宽的频带，低频L1未捕获的信号由高频H1捕获，并依此原理继续往下分解[15]。因此该算法对信号的低频以及高频部分都能进行精确分解。从而可大大提高信号分解的完整性。

图3 小波包3 层分解示意图Fig.3 Three-layer wavelet packet decomposition

图中信号S的分解关系[15]为

2.2 小波包能量提取

由小波的正交性可得：

其中

将分解信号x(t)的平方在无线域上积分即可得到信号f(t)的总能量为

3 扁疤损伤激励引起的轮轨动态响应

3.1 钢轨平顺状态对应的响应

首先考虑钢轨表面为随机不平顺状态，随机不平顺采用中国高速轨道谱，设定高速列车的运行速度为250 km/h，一位轮对左侧设置车轮扁疤[16]。通过上文所述的动力学模型计算得到车辆和轨道系统的动力学响应如图4 和图5 所示。

图4 无扁疤状态对应的垂向振动加速度图Fig.4 The vertical vibration acceleration corresponding to the no-scar state

图5 有扁疤状态对应的垂向振动加速度图Fig.5 The vertical vibration acceleration corresponding to the flat scar state

由图4 和图5 中可以发现，当左轮出现扁疤故障时，会对左侧垂向振动响应产生影响，因此下文中主要分析有扁疤一侧的垂向振动响应。

3.2 动力学响应均值特征

对于动力学响应时域信号的分析常采用均值作为特征，对信号作均值化处理之后，能更好地描述信号的全局特征。

图6 是动力学响应均值随扁疤深度增大的变化规律。可以看出，在有、无钢轨不平顺激励下，扁疤深度变化时，轮对与轴箱的均值分布波动较大，且并不规则，车体、构架以及钢轨上的响应均值没有明显变化，因此以动力学响应时域信号均值作为评价量，难以量化识别车轮扁疤。

图6 垂向振动响应均值图Fig.6 Mean values of vertical vibration response

3.3 动力学响应最大值特征

最大值能体现时域信号数据的程度最高点以及波动情况。图7 给出了动力学响应最大值随扁疤深度增大的变化规律。

图7 垂向振动响应最大值图Fig.7 The maximum vertical vibration response

由图7 可以看出，在有、无钢轨不平顺激励下，扁疤深度变化时，车体与构架上的响应最大值没有明显变化，轮对与轴箱上的响应最大值略有变化。但钢轨加速度信号最强，且随着扁疤深度增加，最大值分布波动明显，不呈线性关系。因此以动力学响应时域信号最大值作为评价量，同样难以量化识别车轮扁疤。

3.4 动力学响应能量特征

采用小波包分解方法，对动力学响应时域信号进行分析，轮轨之间考虑了钢轨平顺、不平顺以及叠加粗糙度3 种激励状态。

图8 是车体、构架、轴箱、轮对以及钢轨的响应能量图，在钢轨不平顺叠加粗糙度、钢轨不平顺以及钢轨平顺3 种激励状态下，能量值逐级减少，其变化趋势是一致的。

图8 垂向振动响应能量图Fig.8 Vertical vibration response energy

随着扁疤深度的增加，图8a）和图8b）中车体与构架的响应能量值都无明显的波动，但轴箱、轮对以及钢轨的响应能量值较大，如图8c）、图8d）和图8e）所示。其中钢轨小波包能量值与扁疤深度之间几乎呈线性关系，因此宜采用钢轨振动响应识别车轮扁疤。

3.5 异侧钢轨能量特征

图9 是钢轨右侧加速度响应下的小波包能量图，可见随着扁疤深度的递增，能量并没有出现增长或波动的迹象，并且其能量大小仅与线路随机不平顺相关。

图9 右轨垂向振动响应能量值图Fig.9 The vertical vibration response energy values of the right rail

对比图8、图9 可见，通过钢轨振动加速度识别车轮扁疤时，需检测与车轮扁疤同侧的钢轨。

4 扁疤冲击位置的影响

列车在运行过程中，当车轮扁疤冲击在测点位置上时其信号程度最强，如图10 所示。在钢轨的车轮扁疤冲击点布置传感器能实现对扁疤的检测，但在列车实际运行过程中，扁疤冲击钢轨的位置具有随机性。

图10 车轮扁疤与传感器测点位置示意图Fig.10 The schematic diagram of the position of the wheel's flat scar and the sensor measuring point

为了得到车轮1 个周长范围滚过钢轨时，钢轨的振动响应，在钢轨上约1 个车轮周长距离即2.9 m范围内布置了10 个测点。

杨光等[5]通过对高速车辆轮轨冲击动力效应进行仿真分析得出当车速高于200 km/h 时，车轮扁疤长度需要限制在35 mm 以内，因此下文将主要分析扁疤长度在35 mm 以内的工况。

在仿真运行中，设置平顺、钢轨不平顺以及叠加粗糙度3 种激励状态，其分析结果如图11、图12以及图13 所示。

图11 钢轨平顺状态下各测点能量分布图Fig.11 Energy distribution of each measuring point under smooth rail condition

图12 钢轨不平顺状态下各测点能量分布图Fig.12 Energy distribution of each measuring point under rail irregularity

图13 钢轨不平顺叠加粗糙度状态下各测点能量分布图Fig.13 Energy distribution of each measuring point under the condition of rail irregularity superposition roughness

从图11～图13 可以看出，当无扁疤故障时其能量值明显低于有扁疤故障，并且在测点56.26 m 处即车轮滚动至半个周长范围时，其能量值明显高于其他位置，可近似视其为扁疤冲击位置。能量值变化先是不断增加而后呈减小的趋势，在56.26 m 测点处达到最大。

由此可知钢轨振动加速度幅值的增大区域出现在扁疤深度大于0.05 mm 之后，距离车轮扁疤与钢轨冲击点0.58 m 的范围内，在车轮扁疤与钢轨冲击点处出现峰值。

综上所述，在列车运行过程中，由于车轮扁疤对钢轨的冲击具有随机性，若要在钢轨上实现对扁疤故障的检测，在钢轨上布置单个加速度传感器，当扁疤冲击点与传感器距离在0.58 m 内时，均可检测出车轮扁疤故障。

5 结论

基于车辆-轨道耦合动力学理论，仿真得到车轮扁疤激扰下CRH380B 高速列车垂向振动加速度响应，通过均值、最大值以及小波包能量法3 种方法对垂向振动响应数据的分析。得出以下结论：

1） 以动力学响应时域信号均值、最大值作为评价量，难以量化识别车轮扁疤。

2） 当车轮扁疤与钢轨测点位置重合时，所提取到的信号强度足，线性特征明显，且左侧车轮出现扁疤故障时，对右侧钢轨振动影响较弱。

3） 在列车运行过程中，由于车轮扁疤对钢轨的冲击具有随机性，在钢轨上布置单个加速度传感器，当扁疤冲击点与传感器距离在0.58 m 内时，可检测出车轮扁疤故障。

本文中研究得出了扁疤冲击点与传感器识别距离范围的关系，若要量化识别车轮扁疤，还需对传感器布置间距和传感器数量做进一步的研究。