分布式驱动电动汽车自适应巡航控制策略研究
2024-03-21胡胜利张缓缓江忠顺常笑宇
胡胜利,张缓缓,江忠顺,常笑宇
(上海工程技术大学 机械与汽车工程学院, 上海 201620)
自适应巡航控系统(Adaptive cruise control,ACC)实时控制主车的车速和主车与前车的距离,能够提高道路的利用率与驾驶的舒适性、安全性与经济性,是智能驾驶技术的一个重要组成部分,也是实现完全自驾的基础;其发展经历了预先距离控制、定速巡航、高速工况的自适应巡航、低速起-停城市工况自适应巡航等几个阶段。在间距策略方面基本形成了以固定车间时距(Constant time headway, CTH)和可变车间时距(Variable time headway, VTH)的为基础的可变间距策略。后者是ACC 系统计算纵向安全距离主流趋势[1-2]。在ACC 系统控制器设计一般采取分层控制的控制架构[3],主要区别是实现上层控制器采取的理论的不同,如PID 控制,最优控制,滑膜变结构控制,模糊控制,模型预测控制,神经网络控制。其中MPC 对模型精确性要求不高[4],能有效解决多目标、非线性优化问题[5],在车辆控制中得到了广泛研究[6-9]。
此外,由于能源与环境问题人们对自适应巡航系统的研究也逐步从燃油汽车过渡到混合动力汽车,纯电动汽车等领域。Vajedi 和Azad[10]针对丰田普锐斯插电式混合动力汽车(PHEV)采用非线性模型预测控制(NMPC)的方法设计ACC 控制器,并用标准循环工况、山区工况进行验证结果表明NMPC可使总能源利用率提高19%。Luo 等[11]对混合动力汽车(HEV)采用NMPC 控制方法设计控制系统实现了车辆的跟车性能与燃油消耗率之间的协调。初亮等[12]对前轴驱动的电动轿车,考虑外界环境风速和坡度对控制系统的干扰,提出了一种自适应巡航纵向控制方法,与传统的PID 控制方法相比,在动态跟随和稳态保持中对期望加速度的跟随效果较好。赵立娜[13]采用分层分工况的控制策略,对电动汽车的ACC 系统进行优化,提高了ACC 系统的适应性。文献[14-17]对纯电动汽车多目标协同控制的ACC 系统展开研究。解来卿等[18]基于MPC 理论设计的ACC算法,实现了分布式驱动电车的安全与节能的协同优化。周苏等[19]基于趋近律的滑模控制理论设计了自适应巡航控制系统对变速直线工况和曲率较大的弯道工况具有良好的跟踪能力。分布式驱动电动汽车响应速度快,传动效率高,空间利用率高等特点,集合电气化、智能化是汽车产业发展的必然趋势,有必要对其进行扩展性研究。
在前者研究的基础上对ACC 系统的适应性进行了拓展。首先针对雷达对坡道、弯道的探测距离存在偏差的问题设计了间距补偿策略。对于ACC系统中MPC 的上层控制算法难以同时保证预测时域和模型精度问题,采用变步长离散化的方法对模型进行离散化处理。下层控制中,以车辆整体驱动效率最优为目标设计了稳态直线工况、弯道行驶工况的期望力矩的分配策略,兼顾了车辆的节能需求。最后对ACC 系统的控制策略在稳态直线道路启停跟随工况、坡道稳定跟随工况、弯道稳定跟随工况进行了仿真验证。
1 整车控制策略
自适应巡航系统以MPC 控制器作为上层控制器,下层控制包括车辆逆纵向动力学模型、逆驱动、制动系统及力矩分配策略。整车控制器(Vehicle control unit, VCU)系统结构图如图1 所示。
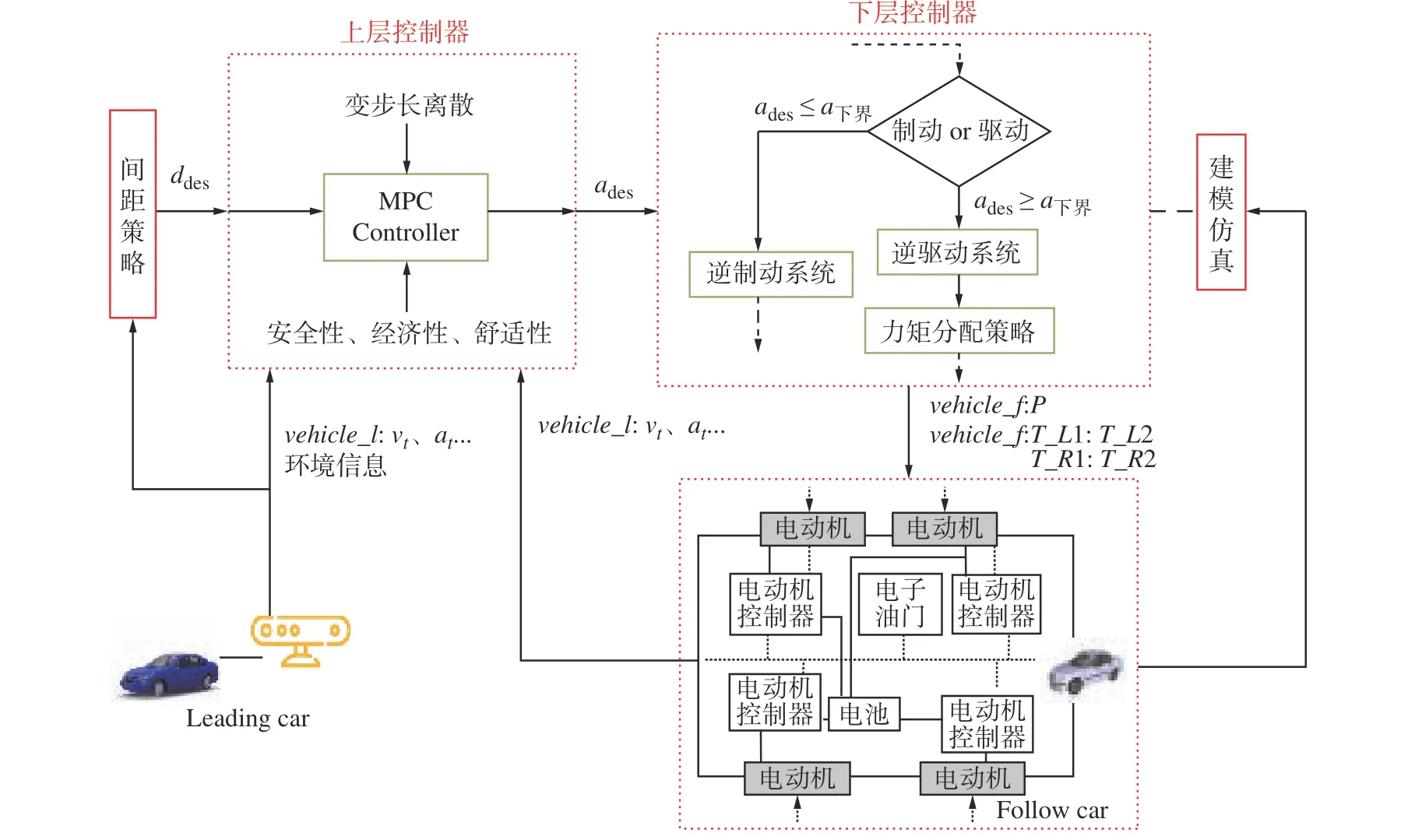
图1 系统结构图Fig.1 System structure
图1 中,环境信息是通过毫米波、激光雷达、摄像头、转速传感器等,来获取前车速度、加速度,主车的速度及其它们之间的航向角。通过非线性的基于可变车头时距(Variable headway time, VTH)的间距策略计算得到期望的跟车间距ddes。ddes及前车、主车的速度、加速度作为上层控制器的输入,在考虑安全性、经济型、舒适性的基础上,通过变步长离散化的MPC 算法,计算得到下层控制器的输入期望加速度,下层控制器通过设计的制动驱动切换逻辑,进入逆制动或驱动系统,得到总的力矩需求,最后经过力矩分配驱动分布式驱动电动汽车行驶,实现兼顾节能的ACC 系统实时跟踪功能。
2 安全距离模型与弯道、坡道的间距补偿
Jiang 等[20]考虑驾驶员对不同相对车速做出的反映情况不同,引入非线性因素,改进的车头时距模型描述如下:
式中:th为 车头时距;th0为车头时距初值;kv、kv0、ka为定值参数;vr为目标车辆和主车间的相对速度;al为前车加速度;v1为前车车速;vf为本车车速。
式中af为本车加速度。两车之间的期望间距ddes表达式为
式中:x0为两车之间的最小安全间距,x0=3 m 。
雷达识别出来的距离信息是两车车辆之间的直线距离,所以当自适应巡航车辆或者跟踪车辆在弯道、坡道中行驶时,相对距离信息都不准确。因此,需要建立车辆过弯、坡道时的道路模型,通过一定的算法对车辆的车间距离进行补偿纠正。
1)弯道工况的补偿算法模型[21]
式中:s为弯道工况下实际的车间距离;l0=drcosφ-Rsinα,dr为雷达探测到的距离, φ为目标车相对于主车的方位角; α为两车对应的圆心角;R为简化后的弯道半径。
2) 坡道间距补偿策略
车辆行驶上坡道到驶离坡道的过程可划分为3 个阶段:驶入坡道阶段、坡道上行驶阶段和驶离坡道阶段。当前车在坡道上行驶而主车在直道路面行驶的工况定义为上坡工况,前车和主车都在坡道上行驶的工况定义为坡中工况,当前车驶离坡道于直道上行驶,且主车仍在坡道上行驶时,定义该工况为下坡工况。车辆上下坡模型如图2 所示。

图2 车辆上下坡模型Fig.2 Vehicle up and down slope model
由图2 可知,模型主车和前车之间的真实车间距可以表示为:
式中:d0为水平道路的距离;d1为坡道上车辆所在位置到坡底的长度在水平道路上的投影;dact为实际的车间距离; θ为坡道角度。
设置该仿真工况的初始条件为:前车开始以25 km/h 速度减小并保持较小的速度在坡道上行驶,主车以25 km/h 的初速度跟车行驶。其中坡道坡度为10%。坡道距离对比仿真结果如图3 所示。

图3 坡道距离对比Fig.3 Contrasting distance of ramps
从图3 中可以看出:在9 s 之前两车均在直道上行驶,雷达检测到的车间距离和补偿策略下的车间距离保持一致;在9 s 时前车驶入坡道,此刻开始补偿策略下的车间距离开始大于雷达测得的实际间距;18 s 时主车行驶到坡道上,雷达检测到的车间距离和补偿策略下的车间距离又重新保持一致,设计的间距补偿策略有效。
3 ACC 上层控制
基于变步长离散化的方法对ACC 系统进行优化设计,在保证较长预测时域的基础上提高ACC 系统的精确性和实时性,考虑分布式驱动车辆的安全性经济性和舒适性等因素设计ACC 系统的上层控制策略。
3.1 系统纵向动力学建模
分布式车辆纵向动力学模型由频率响应法辨识得到,传递函数为
式中:af为分布式驱动车辆的实际加速度;afdes为车辆的期望加速度;Ks为系统增益;Ts为1 阶系统时间常数,系统延迟比传统车辆小。
主车和前方车辆的车间运动学模型可以表示为:
式中:vrel为前后车辆相对车速;sl和sf分别表示前车的位移和主车的位移。
定义系统的状态变量x=[dact,vrel,af]T,系统的控制变量u=afdes。则系统的纵向动力学模型可以表示为:
式中: Φ,Γ和Ψ 均为系统的系数矩阵; η为系统的输入干扰量。
3.2 基于变步长的离散方法
为了同时兼顾模型精度和预测时域,在前半部分、后半部分分别采用短步长的零阶保持器(Zero-Order-Hold, ZOH)和采取长步的1 阶保持器(First-Order-Hold, FOH)对信号进行处理。
零阶保持器G0(s)的传递函数可以表示为
1 阶保持器G1(s)的传递函数可以表示为
3.3 求解离散模型
设整个预测时域为Np(Np=60)按照变步长离散化的方法,对分布式驱动车辆纵向动力学模型的预测时域进行分割处理,在第Ns(Ns=30)步将预测时域划分为两部分,第一部分时间区间和第二部分时间区间分别为k=0,1,2,···,Ns和k=Ns+1,Ns+2,...,Np对于第一部分,即时间k=0,1,2,...,Ns,将纵向动力学模型以t1为步长,使用零阶级保持(ZOH)对模型进行离散化处理。首先设计增广的状态矢量zs1=[x uµ ]T,则式子可以改写为
对矩阵Gs1t1进行矩阵指数运算,并采取零阶保持进行离散化,得
式中:Φs1=I3+Φt1,Γs1=Γt1,Ψs1=Ψt1,I3=R3×3是一个单位矩阵。
得到的离散化后的车辆纵向动力学模型为
在预测时域的第二部分(k=Ns+1,Ns+2,···,Np)以t2为步长,使用1 阶保持对模型进行离散化处理。首先设计增广的状态矢量。zs2=[x uµt2u˙t2µ˙]T,令A=[Γ Ψ ],则式子可以改写为
对矩阵Gs2t2进行矩阵指数运算,并采取1 阶保持进行离散化,得
式中:Φs2=I3+Φt2+(Φt2)2/2,A1=At2+ΦAt22/2,A2=At2/2,I2=R2×2。
求解可得离散化后的车辆纵向动力学模型为
假定忽略输出干扰,则系统输出可以表示为
3.4 ACC 系统约束条件和性能指标
1)安全性指标[18]
式中 ε1和 ε2分别为相对距离误差与速度误差二范数的权重系数。
2)经济性指标
电动汽车的能耗量随着汽车加速度的增加而变大[22],所以车辆的节能性指标可以表示为
式中 ε3节能指标的权重系数。
3)驾驶舒适性指标
约束方程为:
式中:umin和umax分别为加速度的下限值和上限值;
综合考虑以上量化指标,进行线性加权,得到代价函数
式中: ω2为二次项权重系数; ω1为一次项权重系数;c为常数。
3.5 预测优化问题建立
推导系统状态方程、综合性能指标和约束条件,可以得到基于模型预测控制的预测优化问题,表达式为
式中:
3.6 预测优化问题的应用处理
3.6.1 纵向动力学模型反馈纠正
设在一个预测时域内的初始时刻为0,在k时刻车辆的实际状态值为x(k),通过k-1 时刻预测得到的k时刻的预测值为x(k|k-1),车辆纵向动力学模型的状态量和预测值之间的偏差为e(k) , 则e(k)可以表达为:
其中,
将k时刻的误差反馈给k+ 1 时刻的车辆状态值,对其进行校正,纠正后的k+ 1 时刻的预测状态值可以表示为
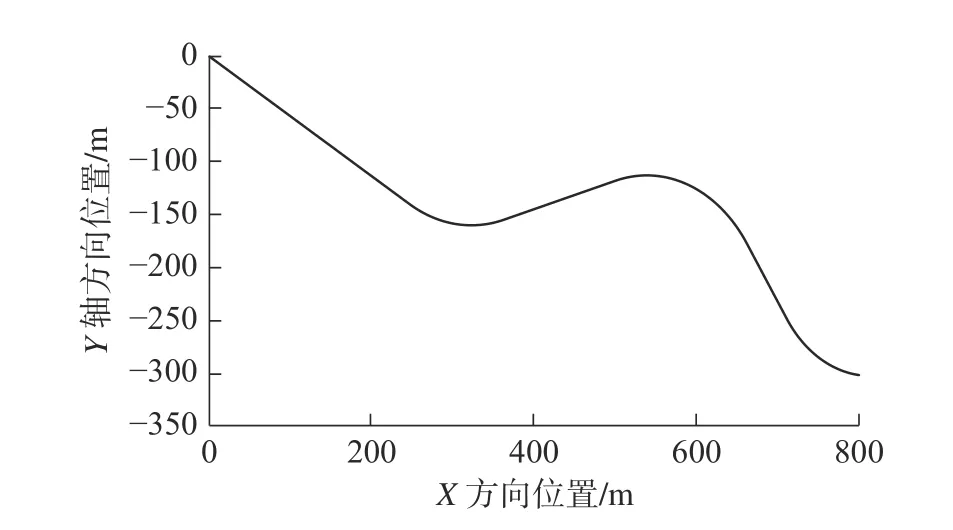
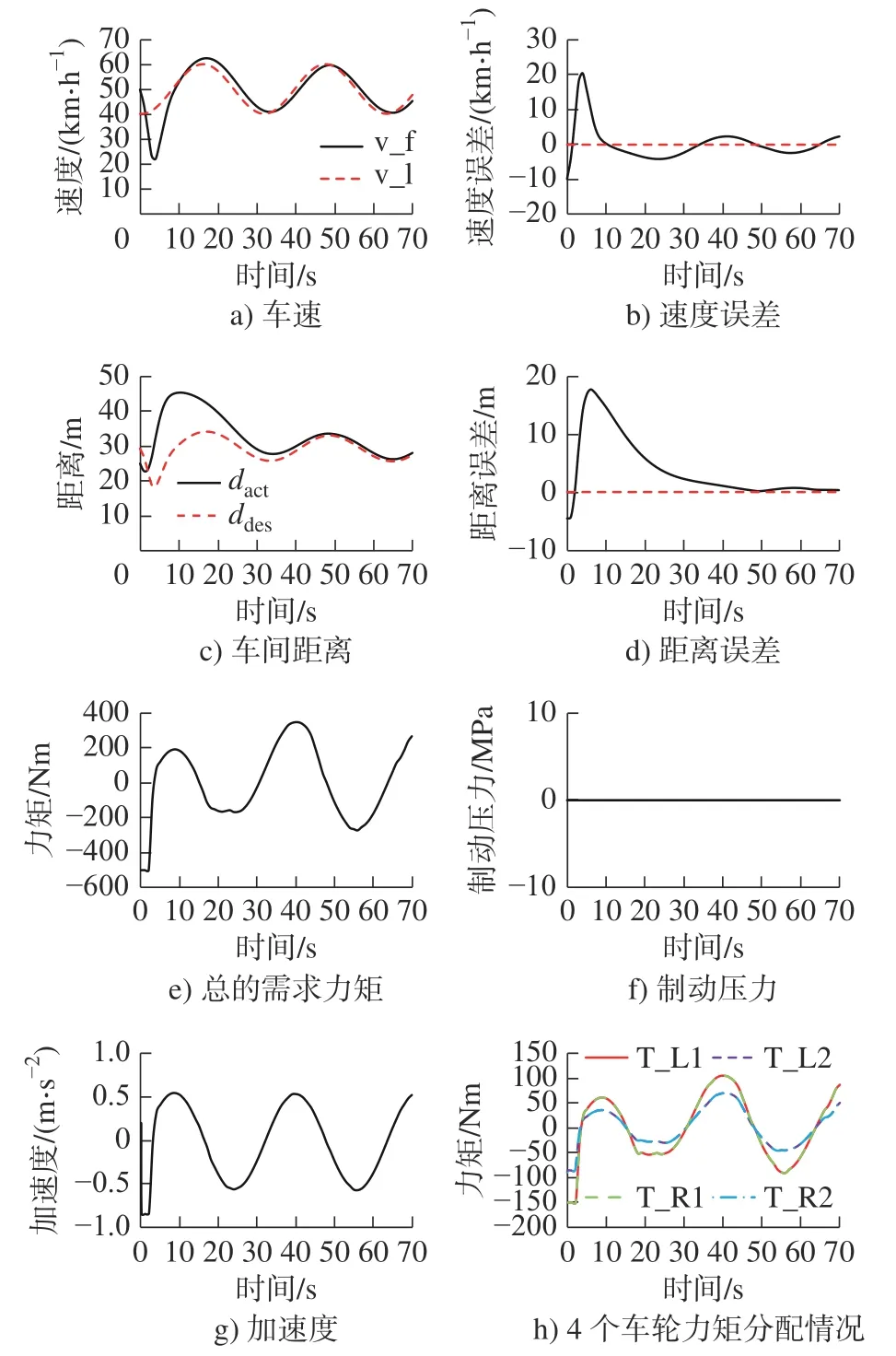
式中He为校正矩阵。0 式中: 3.6.2 向量松弛因子扩展求解可行域 对其约束条件进行松弛处理可以得到: 对约束条件进行边界松弛处理后还需要对松弛因子进行限制,使得优化问题在恰当的限制条件下求出可行解,则损失函数可以写成 式中:Υ为向量松弛因子, Υ=[r0,r1,r2,r3]T; Z为系数矩阵, 对模型预测控制优化过程在出现的偏差和可能出现非可行解问题进行处理后,采用内点法对预测优化问题进行求解,得到每个控制周期内的可行解U,其对应的控制输入量序列和松弛因子序列为: 4.1.1 逆驱动模型 根据期望加速度计算出期望的电动机转矩,即 式中:Tdes为分布式驱动电车所需要的驱动力矩;Ft为驱动力;G为汽车重力;ades为期望加速度;f为滚动阻力系数;CD为空气阻力系数;A为迎风面积;u为相对速度; ε为计入旋转质量惯性力偶矩后的汽车旋转质量换算系数;m为车辆的整备质量;r为车轮的有效半径。 4.1.2 逆制动系统模型 暂不考虑制动能量回收,但是优先由电机的反向力矩对车辆产生制动力,当电机模块输出的制动力不能满足总的需求制动力,液压制动模块提供补偿的制动力。由车辆运动平衡关系建立车辆的行驶方程,可以得到制动力。 4.1.3 驱动制动的切换逻辑 考虑车辆模型基于CarSim/Simulink 建立,在CarSim 平台以给定车速带档滑行为基础拟合出车辆加速度与车速的关系曲线,并以此为基准线设计驱动/制动切换逻辑。为防止频繁切换造成差的驾驶体验及执行器件的疲劳损伤,对求得的切换基准逻辑设置一定的加速度门阈值j,参考文献[23-26],取j= 0.1。 分布式驱动车辆通过四轮独立驱动实现车辆的期望输出动作,所以经过上文策略计算得到车辆的需求力矩后,需要对总的需求力矩进行分配,使得力矩更加合理的施加到每个车轮上。 4.2.1 直线行驶工况下驱动力矩分配策略 1)目标函数 选取驱动系统总的驱动效率为性能指标,利用最优控制理论设计总需求驱动力矩的分配策略。车辆直线行驶时,认为4 个车轮转矩相等且等于电机转矩,且都表示为n。分布式驱动车辆驱动系统的驱动效率 ηe可以表示为 优化受到轮胎附着椭圆、电机输出的转矩受到本身性能的限制、直线行驶无横摆力矩的需求、同轴间采取平均分配的策略等条件的约束,基于驱动效率最大的转矩分配策略,车辆驱动系统转矩分配的优化问题可以写为: 式中:Fx0为最大纵向驱动力,Fy0为最大侧向力。 基于建立的分布式驱动电动车辆模型,对直线行驶工况的力矩分配策略进行有效性检验。设置车辆以60 km/h 的速度在直线路面匀速行驶,仿真结果如图4 所示。 图4 直线行驶下驱动效率对比图Fig.4 Linear drive efficiency comparison 仿真结果表明直线行驶工况下,优化的总驱动效率比均分的总驱动效率得到提高。 4.2.2 弯道行驶工况下驱动力矩分配策略 考虑自适应巡航车辆主要工作在稳定工况,此时由阿克曼转向模型、瞬心定理可得到 电机的转速可以近似等于车轮转速,即: 式中:nfl,nrl,nfr,nrr分别为内前轮、内后轮、外前轮、外后轮转速,近似等于轮毂电机转速n。 车辆以一定车速转向行驶时,基于驱动效率最大的转矩分配策略同样适合,求解的约束条件和目标函数,稳态转向工况下的转矩分配问题可以表达为: 弯道行驶工况初速度设为50 km/h,加速到60 km/h 后,车辆先保持左转弯,直行后右转。驱动效率的仿真的结果如图5 所示。 图5 弯道行驶驱动效率对比图Fig.5 Bend drive efficiency comparison 仿真结果表明优化后转矩分配策略在弯道工况下,整体的总驱动效率高于均分的总驱动效率。 基于CarSim/Simulink 建立纯电动汽车的整车动力学模型和控制策略模型,选取典型的直线道路启停工况和坡道稳定跟随工况、弯道稳定跟随工况对本文所设计的策略进行验证。 选用4 个电压为72 V,额定功率为5 kW 的无刷直流电机(Brushless DC motor drive, BLDC)作为汽车的驱动电机。在Simulink 中搭建直流无刷电机模型,如图6 所示 图6 直流无刷电机模型Fig.6 Brushless DC motor model 为获得理想的加速曲线,不断调整PID 的比例系数KP、积分系数KI、微分系数KD及电流反馈系数Kl。得到电机控制系统的参数,如表1 所示。 表1 电机控制系统参数Tab.1 Motor control system parameters 选用CarSim 中的E-Class,Sedan 为基准车,具体参数如表2 所示。 表2 车辆的基本参数Tab.2 Vehicle's basic parameters 在该工况下,定义主车的初始速度10 km/h,目标车辆车速在0 ~ 12 km/h 之间波动,初始车间距离为20 m,直线道路启停工况仿真结果如图7 所示。dact为实际跟车距离,ddes为期望跟车距离。 图7 直线道路启停跟随工况仿真结果Fig.7 Simulation results of straight road stop & go following condition 从仿真结果图7a)~图7d)中可以看出:初始阶段前车车速为零,主车减速行驶,车间距离减小;4 s左右两车均停止,随后主车跟随前车加速行驶,但主车车速不能很快跟上前车,实际车间距离拉大;12 s后主车车速大于前车车速,实际车间距离减小并逐渐靠近理想的车间距离;在40 s 后,距离误差缩小为1 m 以内,自适应巡航车辆进入稳定跟随前车状态,速度误差也逐渐靠近0,速度跟踪效果较好。整个过程中,实际车间距离均大于理想的车间距离,符合安全性要求。从图7g)所示的加速变化曲线看出,车辆加速度的波动范围保持在-1.5 m/s2~ 1 m/s2之间,无频繁波动的情况出现,有较好的驾驶舒适性和经济性。初始阶段主车急减速,对比图7e)、图7f)和图7h)可以看出,初始的制动力由电机反向力矩和制动器共同作用,其它情况下的力矩输出和力矩分配均可以很好的满足车辆的动力性和制动需求,设计的策略可以较好的跟踪启-停工况的车辆。 在该工况下,主车的初始位置在平面道路,初始速度为40 km/h,目标车辆的初始位置在坡度为10%的坡道上,目标车辆先以40 km/h 的速度匀速上坡行驶,之后车速在40 ~ 60 km/h 之间波动,初始车间距离为40 m。仿真结果如图8 所示。 图8 坡道稳定跟随工况仿真结果Fig.8 Simulation results of stable following condition of a ramp 从仿真结果图8a)和图8c)中可以看出:7 s 之前主车加速行驶,车间距离变小;在7 s 时,主车上坡,车速突然减小,实际车间距离拉大;18 s 后自适应巡航车辆稳定跟随前车行驶,整个过程速度跟踪效果较好。图8b)和图8d)也表明主车在从直道驶向坡道时,速度误差和间距误差有较大的变化,但很快两种误差值均缩小到0 值附近,满足跟踪需求和安全性要求。从图8e)和图8h)中可以看出,在7 s时车辆输出力矩突然增大,之后均输出较大的力矩,符合正常行驶情况。从图8g)可以看出,在10 s 旁边加速度有轻微波动,之后均能平稳输出,整个过程车辆舒适性和经济性较好。从图8f)中可以看出,主车输出的制动压力为零,表明电机的反向力矩满足车辆总的制动力所需。 在该工况下,车辆行驶路径如图9 所示,车辆先直行,接着在弯道半径为150 m 的弯道左转弯,再直线行驶,最后在弯道半径为200 m 的弯道右转弯后继续直行。弯道稳定跟随工况仿真结果如图10 所示。 图9 车辆行驶路径图Fig.9 Vehicle drive route 图10 弯道稳定跟随工况仿真结果Fig.10 Simulated curves of bend stable following condition 从图10a)中可看出:0 ~ 10 s 之间,主车先减速行驶后加速行驶,车速波动相对较大;10 s 后,车辆可以稳定跟随前车行驶。从图10b)中可看出,两车之间的速度偏差在8 s 后保持在-3 ~ 3 km/h 以内,自适应巡航车辆速度跟踪效果较好。从图10c)中可以看出,车间距离起初车间距离拉大,随后很快稳定跟随理想地车间距离,且实际车间距离一直大于理想地车间距离,车间距离误差也逐渐缩小并保持在0 附近,满足安全性要求。从图10g)可以看出,车辆加速度的波动范围保持在-1 ~ 1 m/s2之间有较好的舒适性和经济性。图10e)和图10h)的力矩分配情况和总需求力矩与加速度变化趋势相同,且同轴间的力矩输出表现一致,速度和距离的稳定响应证明此分配策略可以满足车辆的动力需求,从制动压力为零可以看出,该工况下电机的反向力矩可以独立满足车辆的制动需求。在20 s 左右和55 s 左右,车辆正好在弯道中行驶,总的需求力矩和分配到电机上的力矩均有微小的波动,力矩的分配也略有变动,符合实际行驶工况。 1)设计了坡道和弯道补偿的基于VTH 的间距策略模型,解决坡道和弯道工况下雷达探测到的距离小于实际的跟车距离的问题。 2)基于变步长离散化的方法改进的MPC 算法,在保证较长预测时域的基础上提高ACC 系统的精确性和实时性。 3)设计的转矩分配算法在保证安全跟车的前提下,通过驱动转矩的优化分配,提高了整车的驱动效率。通过仿真结果表明,算法实现了分布式驱动电动汽车ACC 系统安全性、稳定性、经济性的设计要求。
4 考虑力矩分配的ACC 下层控制
4.1 车辆逆纵向动力学系统建模
4.2 驱动力矩分配策略
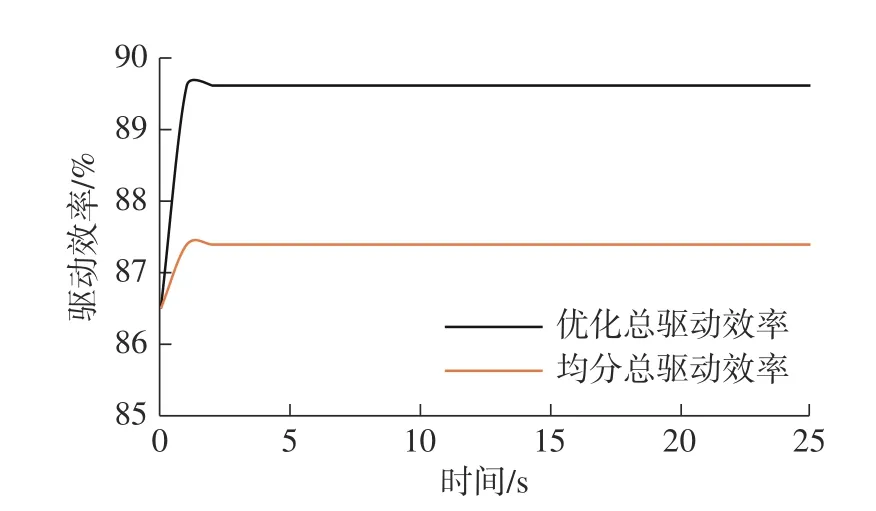
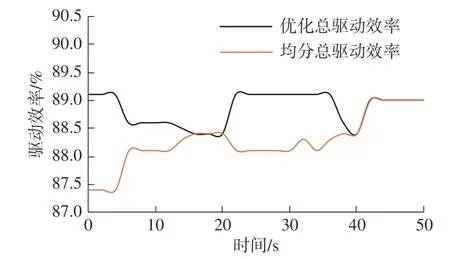
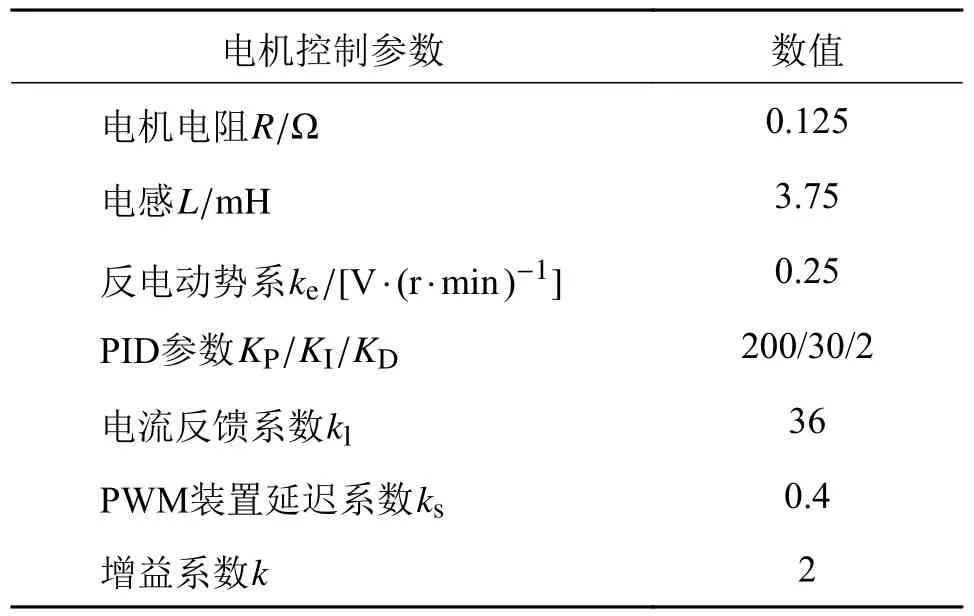
5 仿真实验及分析

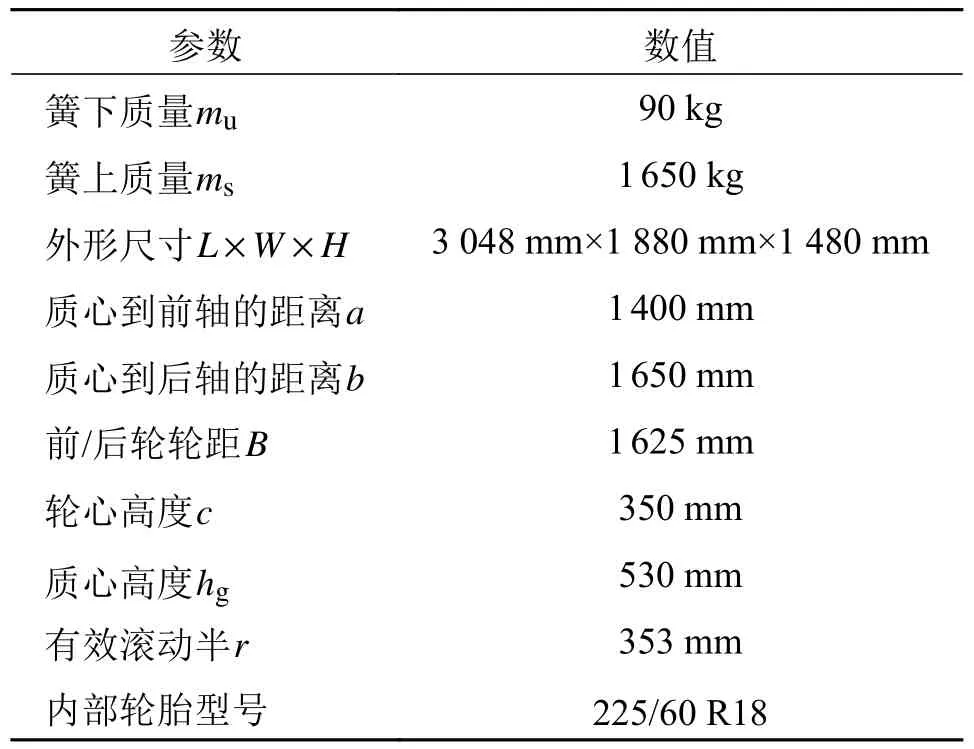
5.1 直线道路启停跟随工况
5.2 坡道稳定跟随工况

5.3 弯道稳定跟随工况
6 结论
