基于ABAQUS 的固体火箭发动机壳体外压屈曲分析 *

耿发贵 ，安自朝 ，何坤 ，康健 ，张鹏坤 ，刘腾跃 ，肖航

（1. 四川航天系统工程研究所，四川 成都 610000；2. 某部驻成都地区第三军事代表室，四川 成都 610041）

0 引言

随着设计制造技术的提升以及超高强度新材料的涌现，固体火箭发动机金属壳体的筒体壁厚越做越薄。在火箭的飞行过程中，会出现固体火箭发动机承受外压的情况，这无疑给越做越薄的固体火箭发动机壳体带来全新的考验。

在以往固体火箭发动机壳体外压屈曲的研究中，研究者的关注点主要在复合材料壳体以及壳体的轴压屈曲上。文献［1-2］利用有限元结构分析法，分别对某纤维缠绕复合材料固体火箭发动机壳体在均布外压作用下以及轴压作用下的稳定性进行了分析；文献［3］介绍了静力轴压下圆柱壳体屈曲应力的工程计算方法，对某固体火箭发动机壳体在复杂受载条件下壳体的屈曲应力进行了分析，并对该火箭发动机壳体屈曲应力如何估计提出了建议。

目前国内对光滑圆柱壳体外压屈曲的研究较多，研究方向主要在于通过特征值计算方法获得圆柱壳体的屈曲模态，再基于特征值屈曲模态引入初始缺陷对圆柱壳体进行非线性屈曲分析。例如，文献［4］利用ANSYS 对外压圆柱壳进行了特征值、几何非线性和几何/材料双非线性屈曲分析；文献［5］采用ANSYS 分析软件引入初始缺陷对某压力容器筒体进行非线性屈曲分析；文献［6］基于单一模态缺陷法和组合模态缺陷法对圆柱壳体外压屈曲进行了仿真分析；文献［7］利用ANSYS 的几何/材料双非线性分析技术对外压圆筒临界压力进行计算；文献［8］将线性屈曲分析的屈曲模态作为初始缺陷的参考值，对受外压海底管道进行非线性有限元分析。

此外，部分研究者采用理论公式对光滑圆柱壳体的外压稳定性能进行了分析。文献［9］采用经验公式和有限元分析方法对外压圆柱壳体的屈曲进行了对比分析；文献［10］对铝合金壳体的外压屈曲计算进行了探讨，分析影响圆筒失稳临界压力的因素；文献［11］介绍了国内科研人员对于圆柱壳体屈曲问题的研究现状以及结果应用。

借鉴上述研究经验，本文以ABAQUS 有限元软件为分析平台，从光壳体入手探索外压屈曲的分析方法，再将此方法应用于固体火箭发动机壳体的外压屈曲分析中，对固体火箭发动机壳体的抗屈曲性能进行了研究。

1 光壳体的外压屈曲分析

1.1 模型概述

壳体筒段长径比为12，壁厚为2 mm。考虑一般壳体两端为封头或法兰等加强结构，约束壳体两端的圆度。壳体材料采用D406A，其弹性模量为210 GPa，泊松比取0.3。

1.2 理论计算方法

圆柱光壳体的外压屈曲理论计算公式众多，本文分别采用Mises 公式和Pamm 公式［12］计算壳体筒段的临界失稳压力。Mises 公式为

Pamm 公式为

式中：Pcr为临界失稳压力；δe为筒体厚度；D0为筒体外径；L为筒体长度；R为筒体外径半径；n为筒体失稳的波纹数，，代入参数求得n为2。

将壳体筒段参数代入，Mises 公式计算得筒体临界失稳压力为0.087 9 MPa，Pamm 公式计算得筒体临界失稳压力为0.098 3 MPa。

1.3 有限元计算方法

通过编写ABAQUS 子程序，实现结构临界失稳压力和屈曲模态预测。一是线性屈曲分析，也叫做特征值分析；另一种是非线性屈曲分析，包括几何非线性和材料非线性。本文中同时考虑了材料非线性和几何非线性的影响。

（1） 线性屈曲分析

线性屈曲平衡方程增量形式为

式中：Ke为弹性刚度矩阵；Kσ(σ0)为初始应力σ0下计算得到的初始应力矩阵；ΔP为外压载荷增量；ΔU为结构位移增量；λ为特征值，也称为应力刚度矩阵的比例因子或载荷因子，结构临界失稳载荷P=λ·P0，P0为施加在结构上的初始载荷。

临界失稳时，ΔP=0，但ΔU≠0，因此的特征值为0，可解出其特征值以及对应的屈曲模态。

有限元分析网格单元类型为四节点壳单元S4R，经过网格独立性验证，网格大小设置为10 mm可以满足要求，在壳体外表面施加1 MPa 外压，计算得壳体的特征值为0.090，则线性屈曲分析壳体临界失稳压力为0.090 MPa，线性失稳模态如图1 所示，可知壳体的临界失稳波数为2，与理论计算的失稳波纹数一致。

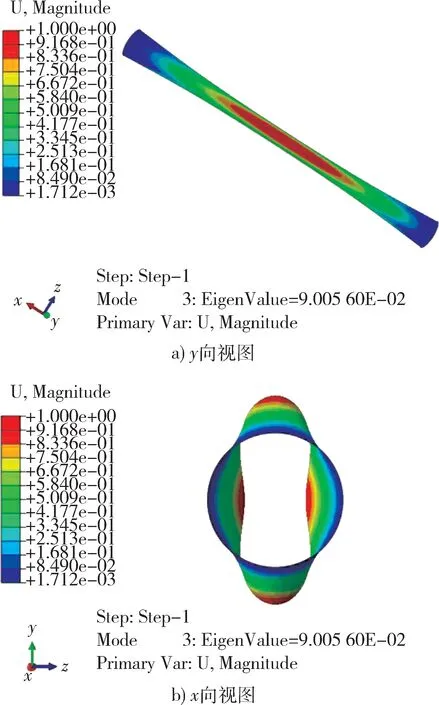
图1 筒体外压作用下线性屈曲模态（放大100 倍）Fig. 1 Linear buckling mode of cylinder under external pressure (magnification 100 times)

（2） 非线性屈曲分析

线性分析方法未考虑结构表面缺陷以及加工精度（圆度、直线度等），计算结果过于理想化；此外线性屈曲仅能计算出壳体的屈曲模态以及临界屈曲载荷，并不能反映出壳体屈曲之后的后屈曲状态，因此要增加非线性分析。

本文的非线性分析同时考虑材料/几何双非线性。材料非线性的实现通过改变材料性能参数，输入材料应力应变曲线，壳体材料屈服强度为1 320 MPa，抗拉强度为1 620 MPa。几何非线性的引入有2 种方法：①直接法，在筒体上直接加扰动或设置缺陷；②间接法，将线性屈曲求得的变形乘以一个比例系数作为缺陷引入，比例系数越大，则引入的缺陷越大。在本文中采用间接法，以线性计算结果为基础，通过编写ABAQUS 关键字输出线性屈曲模态，在非线性计算时通过编写程序引入线性屈曲模态并乘以比例系数作为壳体缺陷，考虑加工精度，引入比例系数0.01。

非线性屈曲分析采用弧长法计算，监测筒体中部一点的位移，分析壳体屈曲过程，加载过程中监测点位移U随载荷比例因子（load proportional factor，LPF）的变化曲线如图2所示。

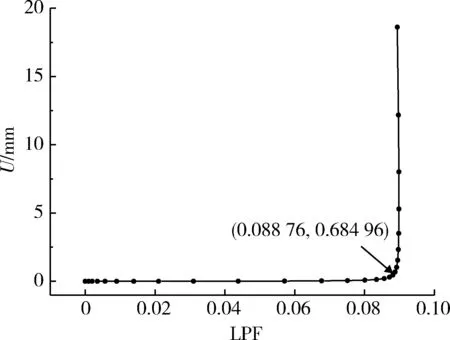
图2 载荷比例因子-位移曲线图Fig. 2 Load scale factor-curve

由图2 可以看出，随着载荷比例因子的增加，监测点的位移逐渐变大；当比例因子增加到一定量时出现转折点，在转折点之前，随着载荷比例因子的增加，监测点的位移缓慢变大，在转折点之后，载荷比例因子只要增加一个微小量，监测点的位移就会出现较大的变化。这与壳体的屈曲过程一致，当外压小于临界失稳压力时，壳体变形量较小，一旦外压达到临界失稳压力，壳体瞬间垮塌，出现大变形。转折点对应的载荷即为壳体临界失稳载荷，通过载荷比例因子和施加载荷相乘可得临界失稳压力为0.088 8 MPa。

通过线性分析方法和非线性分析方法的对比可以看出，非线性分析方法计算的临界失稳压力比线性分析方法的计算结果低了1.3%。

1.4 对比分析

通过以上计算可以得出，有限元计算结果和理论公式计算结果十分接近，为避免计算结果的单一性和偶然性，增加本文计算方法的说服力，改变壳体的长径比，通过多种长径比的光壳体对比分析验证。上述壳体的长径比为12，保持壳体的其他尺寸不变，通过改变壳体长度，研究长径比，分别为14，10，8，6 的光壳体的临界失稳压力的变化。同样采用上述的4 种计算方法，计算结果如图3 所示。

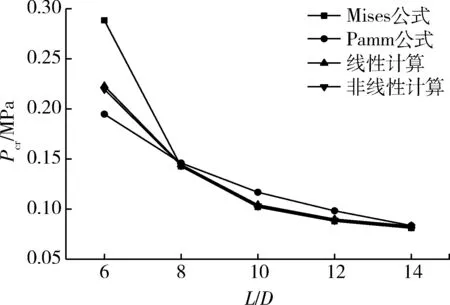
图3 长径比-临界失稳压力曲线图Fig. 3 Length-diameter ratio-critical instability pressure curve

通过图3 中的计算结果可以看出，随着长径比增大，壳体的临界失稳压力逐渐减小，壳体的抗屈曲性能逐渐变差；通过4 种方法的对比计算结果可以看出，当长径比小于8 时，4 种方法的计算结果较为分散，误差较大，但有限元的2 种计算结果介于2种理论公式计算结果之间，相对可靠；当长径比不小于8 时，4 种方法的计算结果相差不大，Mises 公式计算结果和有限元线性计算结果、非线性计算结果十分接近，Mises 公式计算结果最小，线性计算结果最大，而非线性计算结果居中；以Mises 公式计算结果为基准，本文所研究的壳体（长径比为12）线性计算结果误差为2.4%，非线性计算结果误差为1.0%，同样也表明了非线性计算结果更接近于壳体实际屈曲情况。

通过不同长径比的光壳体屈曲分析计算可以看出，以Mises 公式计算结果为基准，当长径比不小于8 时有限元计算结果的误差都在2.7%内，表明本文基于ABAQUS 的壳体外压屈曲分析方法准确可靠，可以用于后续分析计算。

2 带定心部壳体的外压屈曲分析

为了增加固体火箭发动机壳体的刚度，通常会在壳体上增加一定数量的定心部结构，定心部起到与加强圈类似的功能，对壳体的刚度有较大的提升作用。本节将采用第1 节中验证过的有限元屈曲分析方法分析带定心部壳体的屈曲性能变化。

2.1 定心部轴向长度对壳体屈曲性能的影响

保持壳体其他尺寸不变，在壳体中心位置增加一个定心部，其结构如图4 所示。固定定心部厚度为5 mm，分别取定心部轴向长度为50，100，150，200，250 mm，非线性计算同时考虑材料/几何双非线性。

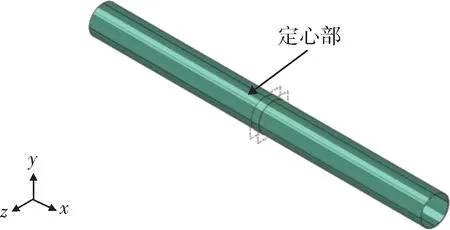
图4 带一个定心部的壳体结构示意图Fig. 4 Schematic diagram of shell structure with a centering part

带不同轴向长度定心部壳体的径向位移随外压的变化如图5 所示，可以看出随着外压增加，壳体的径向位移逐渐变大。当外压增加到一定量时，壳体径向位移变化出现拐点，当外压超过拐点，壳体的径向位移迅速变大。拐点对应的外压即为壳体的临界失稳外压。

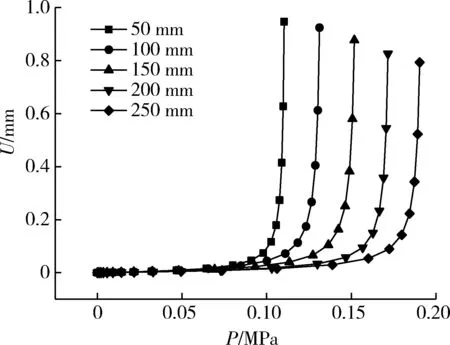
图5 外压-位移曲线图Fig. 5 Curve of external pressure-displacement

不同轴向长度定心部壳体的临界失稳外压如图6 所示，可以看出随着定心部轴向长度增加，壳体的临界失稳外压逐渐增大，且临界失稳外压呈线性增长。定心部轴向长度由50 mm 增加到250 mm，壳体的临界失稳外压提高了73%，表明定心部轴向长度的变化对壳体抗失稳性能有较大的提升作用。可以看出，考虑了材料和几何双非线性计算的结果低于线性计算的结果，但二者相差不大，误差都在1.6%内。

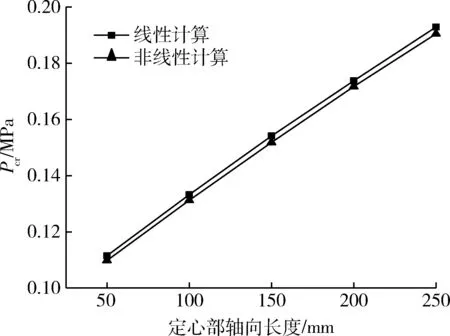
图6 定心部轴向长度-临界失稳压力曲线图Fig. 6 Curve of axial length of centering part-critical instability pressure

2.2 定心部厚度对壳体屈曲性能的影响

保持壳体其他尺寸不变，壳体中心位置设置一个定心部，固定定心部轴向长度为100 mm，分别取定心部厚度为3，4，5，6，7，8，9，10 mm进行外压屈曲分析，计算结果如图7所示。

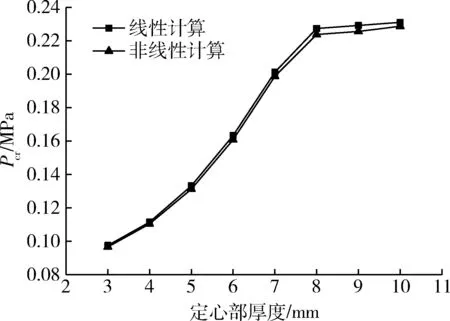
图7 定心部厚度-临界失稳压力曲线图Fig. 7 Curve of centering thickness-critical instability pressure

由图7 可以看出，当定心部厚度小于8 mm 时，随着定心部厚度增加，壳体的临界失稳外压逐渐变大，定心部厚度由3 mm 增加到8 mm，壳体的临界失稳外压变大了1.35 倍；当定心部厚度不小于8 mm时，壳体的临界失稳外压趋于稳定，即使定心部厚度继续增加，壳体的临界失稳外压变化也不会太大。

分析不同厚度定心部壳体在外压作用下的线性屈曲模态，当定心部厚度小于8 mm 时，壳体的屈曲模态类似于图8a）的形态，壳体呈现出整体失稳，失稳波纹数为2；当定心部厚度不小于8 mm 时，壳体的屈曲模态类似于图8b）的形态，壳体两侧局部失稳，局部失稳波纹数为3。当定心部厚度不小于8 mm 时，由于定心部刚度太大，此时相当于将壳体以定心部为界限分为了2 个短圆筒，再增加定心部的厚度，对两侧短圆筒的屈曲性能不会产生太大影响，因此图7 中当定心部厚度不小于8 mm 时，呈现出壳体的临界失稳外压趋于稳定的状态。

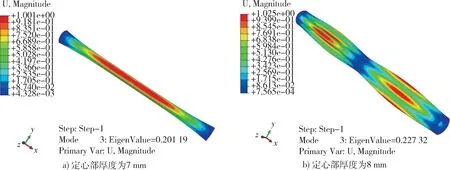
图8 壳体外压作用下线性屈曲模态（放大100 倍）Fig. 8 Linear buckling mode of shell under external pressure (100 times magnification)

2.3 定心部位置对壳体屈曲性能的影响

保持壳体其它尺寸不变，固定定心部轴向长度为100 mm，定心部厚度为5 mm。改变定心部的位置，以壳体左侧端面为原点，分别取定心部位于550，1 100，1 650，2 200，2 750，3 300，3 850 mm 进行外压屈曲分析，其屈曲模态如图9 所示。

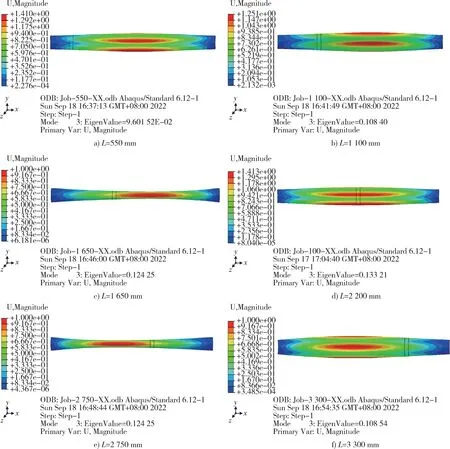
图9 壳体外压作用下线性屈曲模态（放大100 倍）Fig. 9 Linear buckling mode of shell under external pressure （100 times magnification）

由图9 可以看出，以当前尺寸的定心部对发动机壳体进行补强，定心部位于壳体的任意位置，壳体的屈曲模态都为整体失稳，且失稳波纹数为2。定心部位于壳体的不同位置，其屈曲模态存在差异。随着定心部位置向中间移动，壳体的屈曲中心逐渐偏离壳体中心向另一侧移动。以壳体中心截面为对称平面，位于壳体两侧对称位置处的屈曲模态一致，其临界失稳压力也相同。

由图10 可以看出，当定心部位于壳体中心时，壳体的临界失稳外压最大，随着定心部的位置逐渐向两侧移动，壳体的临界失稳外压逐渐减小。将定心部由壳体中心移到距离两侧端面550 mm 处，壳体的临界失稳外压降低了27.9%。

2.4 1 个定心部和3 个定心部计算结果对比

保持壳体其他尺寸不变，固定定心部轴向长度为100 mm，定心部厚度为5 mm。以壳体左侧端面为原点，在1 100，2 200，3 300 mm 处各设计一个定心部进行外压屈曲分析，其线性屈曲模态如图11 所示，其临界失稳压力计算结果如表1 所示。

表1 壳体外压作用下临界失稳压力Table 1 Critical instability pressure under external pressure of shell MPa

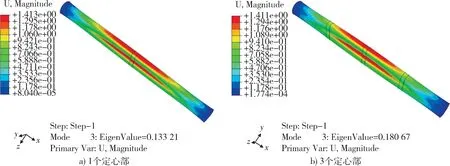
图11 壳体外压作用下线性屈曲模态（放大100 倍）Fig. 11 Linear buckling mode of shell under external pressure (100 times magnification)

由图11 可以看出，在上述尺寸约束下，3 个定心部和1 个定心部的失稳模态都为整体失稳，失稳波纹数为2。表明3 个定心部仍然不足以改变壳体的屈曲模态。通过表1 的计算结果对比可以看出，在上述定心部尺寸约束下，由中心1 个定心部增加到3个定心部均布，临界失稳压力增加了36.1%。

3 结论

文中以ABAQUS 分析软件为平台，通过编写子程序模拟壳体的屈曲过程。光壳体的屈曲分析采用有限元分析法和理论公式计算法对比分析，对计算方法进行验证。将此方法应用于带定心部的固体火箭发动机壳体的屈曲分析中，对固体火箭发动机壳体的屈曲性能进行分析。得到以下几点结论：

（1） 考虑几何/材料双非线性的有限元分析方法计算的临界失稳压力比线性分析方法的计算结果小。当壳体长径比不小于8 时有限元计算方法和Mises 公式、Pamm 公式计算的结果十分接近，计算结果适应性较好，当壳体长径比小于8，Mises 公式和Pamm 公式的计算结果较为分散，有限元计算结果介于二者之间。

（2） 相较于增加定心部的轴向长度，增加定心部的厚度对壳体抗屈曲性能的提升更为显著。定心部轴向长度由50 mm 增加到250 mm，壳体的临界失稳外压提高了73%，定心部厚度由3 mm 增加到8 mm，壳体的临界失稳外压变大了1.35 倍。

（3） 定心部位置越靠近壳体中间，壳体的抗屈曲性能越好。在文中定心部尺寸的约束下，由中心1 个定心部增加到3 个定心部均布，临界失稳压力增加了36.1%。