基于改进支持向量回归的空战飞行动作识别 *

刘庆利，李蕊，乔晨昊

（大连大学 通信与网络重点实验室，辽宁 大连 116622）

0 引言

空军的强大是一个国家强大的重要体现，空军是否强大取决于飞机的质量和飞行员的作战经验，所以通过一些方法使飞行员与飞机进行有效的沟通，是现代战斗机的发展方向。当今空战不仅仅是机炮、导弹等热兵器的对决，更为重要的是电子战，如何有效提升信息的获取是本文研究的方向，而准确的获取自身和敌机的飞行状态是获取有效信息最为关键的一环。

近几十年来，随着科技的发展，出现了越来越多的飞机飞行动作的识别方法，主要有：支持向量机、聚类、神经网络、状态规则匹配法等智能算法。文献［1］采用基于聚类的方法，先提取飞行数据的主要参数，通过趋势识别后得到的机动片段进行聚类划分，缺点在于趋势识别的机动片段难以捕捉准确的机动片段，会对聚类的结果有影响；文献［2］采用模糊支持向量机算法（fuzzy support vector machine，FSVM），解决了支持向量机在处理多分类任务时出现的不可分区域问题，对分类的结果有一定准确性，但是受限于支持向量机的参数c和g，如果参数不能很好地优化，得到的模型也必然大打折扣；文献［3］整体采用神经网络的方法进行分类，对飞行数据的处理采用微分分割的思想建立神经网络的输入，缺点在于神经网络需要大量的数据来支持模型，对于较难获得的飞行数据来说，大量数据的获取是关键性问题；文献［4］采用支持向量机模型，对飞行数据采用状态匹配的方法进行处理，但是处理方法需要人工识别，会导致无法实时地进行处理，也会给飞行员与飞机的交互造成一定程度的障碍；文献［5］采用决策树模型，对飞机飞行的动作先进行分类再进行识别，是一个实时的系统模型，它可以利用真实数据进行动作识别，但效率较低，在瞬息万变、讲求效率的战场上，采用离线的、训练好的模型会极大缩短时间，提高效率；文献［6］采用C-支持向量机模型，先对飞行数据进行降维处理，再将处理后的数据进行模型化训练，缺点在于C-支持向量机模型对多分类问题表现仍然不够理想；文献［7］采用智能算法对飞行规则进行提取，提出了映射突变机制，对目标函数的优化效果较为理想，该方法对于飞行规则提取是可行的，但对于飞行动作识别是远远不够的，需要联合人工智能算法实现；文献［8］采用建立知识库的方式对飞行动作进行匹配，这种方法对于已有的飞行动作可以进行大概的匹配，对于要求较为苛刻的空战和未知的飞行动作则显得难以驾驭；文献［9］采用樽海鞘群优化算法对飞行数据进行提取和匹配，但该算法仅对于部分动作有较好的效果，不具有通用性，难以满足现代化空战的需要；文献［10］采用动态时间调整与马尔可夫算法相结合的方法，对于实时性的表现较好，但是对于复杂的机动识别，应提前建立离线的知识储备库来应对。

综上所述，主要存在以下几点问题：一是现有识别方法处理飞行数据的能力存在不足，对于复杂的飞行动作，仅由基本动作组成的方式处理数据是远远不够的，相似的动作极易发生识别错误的情况；需要对输入数据根据规则进行逐一判断，当需要处理批量数据时，所需识别时间较长；二是识别飞行动作的准确率还存在提升的空间，因此非常有必要提高模型的分类能力和回归能力，并提高判断识别的准确度，所以对空战中飞机的飞行动作识别的研究是非常有意义的。针对以上问题，本文采用麻雀搜索算法（sparrow search algorithm，SSA）和支持向量回归算法（support vector regression，SVR）相结合的方式，提出了强化麻雀搜索支持向量回归（intensify SSA-SVR，ISSA-SVR）的识别方法，采用高斯核函数作为线性核函数［11］，同时利用混沌初始化和小孔成像反向学习策略优化麻雀搜索算法，并利用优化后的麻雀搜索算法对支持向量回归算法的高斯核函数参数进行优化，使其找到最优解，从而达到识别准确的效果。

1 空战飞行态势数据预处理

根据战斗机的实际飞行轨迹和飞行姿态可以将飞机的机动动作看作是一系列复杂的机动动作，而复杂的机动动作又可以分解为一系列具有时间序列的基本飞行动作［12-15］。国际上较为认可的是美国国家航空咨询委员会NASA 提出的7 种基本动作：原状态飞行、加速直线飞行、减速直线飞行、左转飞行、右转飞行、爬升飞行、俯冲飞行。本文将这7 种基本动作归纳为平飞、俯冲、转弯、横滚和爬升五大类。

要对飞机动作进行识别，首先要将飞行动作分解成一系列计算机可识别的数据，该过程是由人工完成的，识别出来的数据是一系列具有时间序列的飞行片段［16-20］。而基本动作也可以分解成不同飞行参数的组合，本文主要研究的飞行参数包括：偏航角ψ、滚转角Φ、俯仰角γ和高度h，基本动作与飞行参数的关系由表1 所示。

表1 基本动作与飞行参数的关系Table 1 Basic flight action division

基本动作往往只是最基本的飞行方式，远远不能满足空战的需要，而飞行员需要掌握复杂的飞行方式，尤其是优秀的飞行员可以熟练使用各种复杂的飞行方式。本文研究的复杂飞行动作有：斤斗、半滚倒转、水平横滚、上升转弯、俯冲转弯、半斤斗倒转和急规避转弯7 种，其编号和动作组成如表2所示。

表2 复杂飞行动作描述Table 2 Description of complex flight movements

以半斤斗倒转为例，将机动动作可以拆分为3类片段：爬升、平飞和横滚。这些动作对于飞行员而言，是最基本的飞行态势，但不会保持一个固定的参数，会允许该参数在一个小范围内浮动。

对于复杂的飞行动作，仅仅由基本动作组成的方式处理数据是远远不够的，相似的动作极易发生识别错误的情况，这种情况是灾难性的，因此准确识别一个复杂动作还需要对变化量及其他条件进行限制。本文对复杂动作进行如下处理：

（1）对于飞行过程中，飞机航向角由350°变为0°的这种极端情况，飞行实际上只变化了10°，但是计算机处理时，会认为转弯了340°，由此对飞行参数进行条件限制，角度的变化量为

（2）对于爬升转弯和俯冲转弯，角度的变化量都是相似的，计算机很难识别飞机的飞行姿态，所以对于高度而言，爬升是正变化量，俯冲是负变化量，假设高度变化量为Δh，爬升则是+Δh，俯冲则是-Δh。

（3）对于俯仰角，其变化量不超过90°，否则会造成失速，导致飞机处于危险的情况，假设俯仰角变化量为Δγ，则Δγ＜ 90°。

2 改进支持向量回归算法

2.1 支持向量回归算法

SVR 是从支持向量机算法（support vector machine，SVM）中衍生出来的，主要针对的是回归问题。通过SVR 算法，可以找到一个回归平面并使得一个集合中的所有数据距离该平面的距离最短。SVR 的模型是一个线性函数f(x) =wTx+b，w和b为不确定的参数，区别于线性回归的地方在于损失函数和目标函数，SVR 在线性函数两侧制造出一个边缘界限，所有落入其中的样本，都不计算损失，这样通过与边缘界限的距离与总的损失来优化模型，达到最优的效果。SVR 的数学模型：；前一部分表示优化目标；后一部分表示代价函数；c为惩罚因子；m为样本个数。损失函数为

式中：ε为线性函数；f(x)与边缘界限的距离；|z|为线性函数f(x)与样本点之间的距离。

此时的模型还不是最优模型，需要加入松弛变量ξi和进行优化，得

其中：ξi为隔离带上边缘之上样本点的纵坐标值，与对应横坐标在“上边缘超平面”上投影的差；而为隔离带下边缘之下样本点，到隔离带下边缘上的投影，与该样本点纵坐标值的差。

在此基础上再次引入拉格朗日乘子μi，，ai，得

使得式（4）左边对各参数的偏导为0，得

满足最优解就需要满足KKT 条件，即

最终得到最优解为

式中：为SVR 较为优秀的高斯核函数。

2.2 强化麻雀搜索算法

麻雀搜索算法虽然具有流程简单、寻优能力强、收敛速度快的优点，但与其他的智能优化算法一样，麻雀搜索算法自身也有一定的局限性，因此，本文先对麻雀搜索算法进行以下几方面改进。

2.2.1 混沌初始化

借助Logistic 映射产生的混沌序列可以解决初始值不敏感的问题，本文利用Logistic 混沌策略来初始化麻雀种群，既可以使种群更加全面地对空间进行搜索，又可以解决因初始值选择不合适而使搜索时间延长的问题。Logistic 混沌策略如下：

式中：X为混沌变量；λ为混沌系数，当λ= 4 时混沌变量X处于全混沌状态。给X赋一个初值x0，便可产生一个麻雀的中期序列［x1，xm］，这个序列就是一个混沌变量，该序列一直迭代下去可不重复地遍历混沌范围。

2.2.2 强化反向学习策略

在混沌初始化之后开始迭代发现者的阶段，当R2＜ST时，麻雀的数量以及多样性会逐步减少，这意味着该算法会随着麻雀数量的减少而陷入局部最优，其中，R1，R2∈[0，1)为预警值；ST∈[0.5，1)为安全值。因此利用类似小孔成像的方式，将反向原理运用到学习策略中解决麻雀搜索算法的问题，如图1 所示。

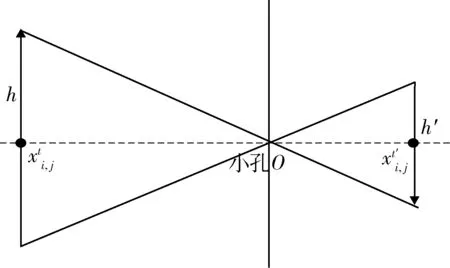
图1 小孔成像反向学习原理图Fig. 1 Schematic diagram of keyhole imaging reverse learning

假设每只麻雀位置变化的范围是［ai，bi］，高度为h的火焰在x轴上的投影为麻雀种群中发现者的位置，其透过小孔成像得到一个高度为h′的倒影，此时的横坐标为，由三角形相似原理可得

当k= 1 时，可得

k= 1 时，小孔成像反向学习就退化为基本的反向学习策略，此时解为固定解，而小孔成像的策略可以通过比例系数k来调整解的空间，得到更完全的解。

本文利用改进后的反向学习策略更新发现者的位置，通过式（8）映射到空间中得到最优解，将原本发现者位置的适应度值与改进后的适应度值进行比较，保留最优的适应度值。小孔成像反向学习策略可以大幅增加发现者的寻优方向，使每只麻雀可以在不固定的区域寻找最优位置，该策略大大增加了种群的多样性，并增强了麻雀全局搜索的能力，减少局部收敛的概率。

2.3 强化麻雀搜索优化的支持向量回归算法

本文利用强化麻雀搜索算法来优化支持向量回归算法，形成新的算法：强化ISSA-SVR 算法。利用该算法的特点进行飞机飞行动作的预测与回归，该算法由强化麻雀搜索算法和支持向量回归两部分组成：

（1） 输入：处理飞行数据，进行归一化处理；

（2） 构建预测与回归的支持向量回归算法；

（3） 利用ISSA 优化SVR 的目标函数，其中包括确定麻雀的参数、混沌初始化麻雀的位置、利用小孔成像原理更新发现者的位置、躲避发现者的位置。

（4） 计算最佳适应度函数，满足目标则停止迭代，否则继续执行3）

（5） 输出：得到最优的SVR 的参数c和g，并以此建立最终的预测与回归的模型，并得到识别的准确率。

ISSA-SVR 的算法迭代图如图2 所示。

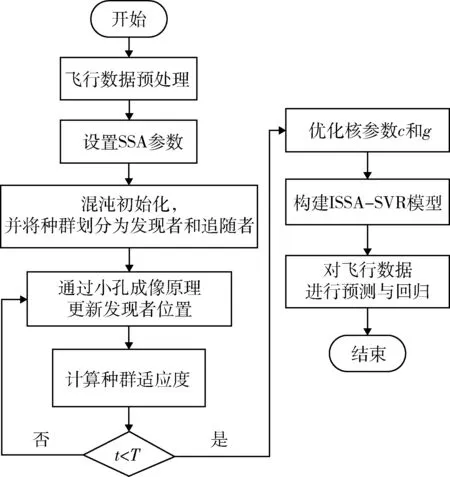
图2 ISSA-SVR 算法流程图Fig.2 ISSA-SVR algorithm flow chart

3 仿真校验

本文采用识别动作的准确率来对算法进行评价，准确率=正确识别的飞行动作个数/输入的飞行动作总和，首先进行参数设置，选取好参数后进行仿真，对基本动作和复杂动作都进行了仿真验证，然后用相同的参数对SVM 算法、FSVM 算法、基于高斯混和模型的聚类算法（Gaussian mixture model，GMM）［20］以及基于自组织图的人工神经网络方法（neural gas）进行仿真对比。

3.1 参数设置

设置算法参数，对算法的最大迭代次数、种群数量、发现者占比、意识到危险的麻雀数量、惩罚因子、高斯核参数进行取值，具体参数设置如表3所示。

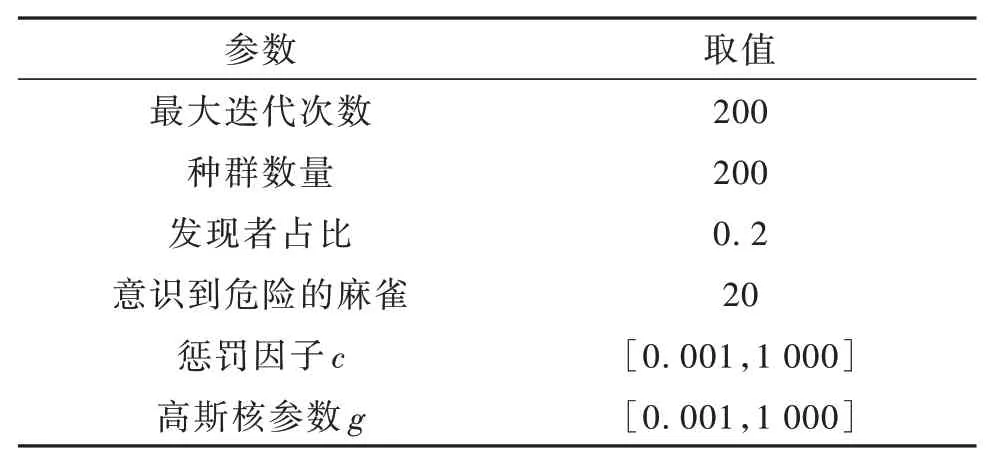
表3 ISSA-SVR 参数设置Table 3 ISSA-SVR parameter setting

3.2 基本动作仿真分析

如表4 所示，ISSA-SVR 对平飞、俯冲、转弯、横滚、爬升等飞行基本动作的识别率最低达到了99.03%，最高达到了100%。

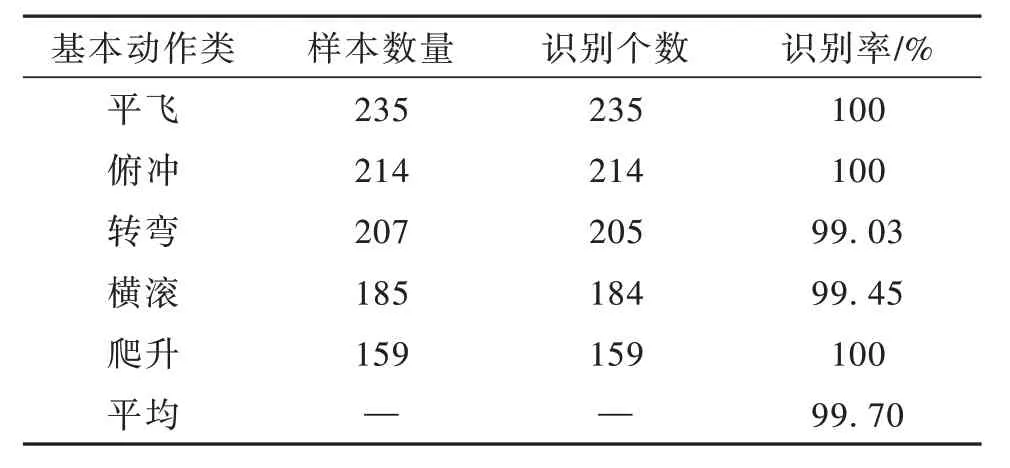
表4 ISSA-SVR 对基本动作的识别率Table 4 ISSA-SVR recognition rate of basic actions

从图3 可以明显看出，ISSA-SVR 算法相较其他几种算法对基本动作识别的准确性有了明显提高。ISSA-SVR 算法对基本飞行动作的平均识别率为99.7%，SVR 算法、FSVM 算法、GMM 算法以及Neural Gas 算法的平均识别率分别为97%，97.5%，88.72%，92.34 %。相较之下，ISSA-SVR 算法对基本飞行动作的平均识别率至少提升了2.2%。

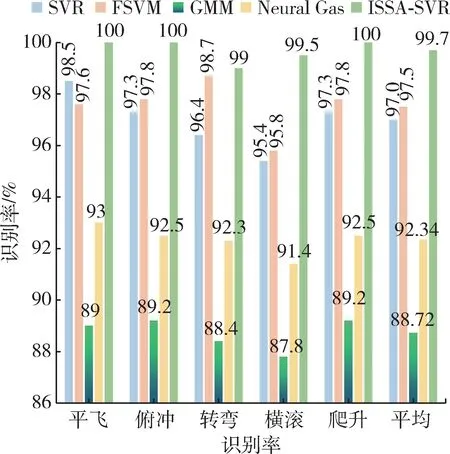
图3 5 种算法的基本动作识别率Fig. 3 Basic action recognition rate of five algorithms

3.3 复杂动作仿真分析

如表5 所示，ISSA-SVR 对飞行复杂动作的平均识别率为95.3%，相较于简单动作，识别率有所降低，这是因为复杂的飞行动作的时间序列连贯性较高，在短时间内会产生多个基本动作，导致识别率下降。斤斗、半滚倒转、半斤斗倒转动作的识别率分别为93.0%，87.5%，94.5%，相较其他复杂动作识别率偏低，这是因为本文采用的是高斯核函数，对非线性的飞行动作识别率会有所降低。

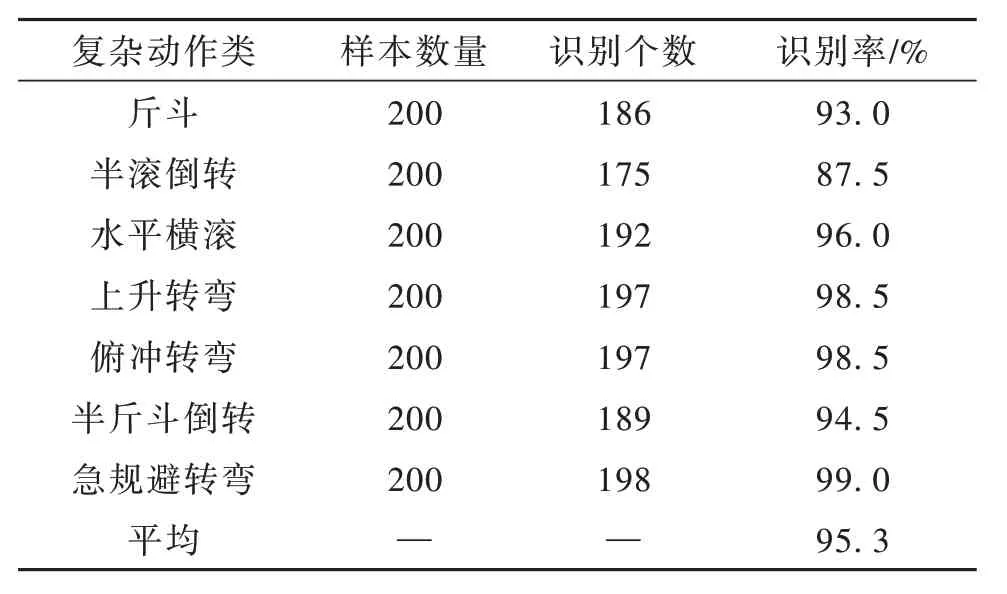
表5 ISSA-SVR 对复杂动作的识别率Table 5 ISSA-SVR Recognition rate of complex actions

从图4 可以明显看出，在对复杂动作的识别中，ISSA-SVR 算法依旧保持优势，这是因为ISSA-SVR算法前期是由ISSA 进行目标函数优化的，得到的最优解远好于其他几种算法。几种算法对复杂飞行动作的平均识别率分别为95.3%，90.8%，91.6%，87%，78.1%。ISSA-SVR 算法对比其他两种算法的平均识别率至少提升了3.7%。

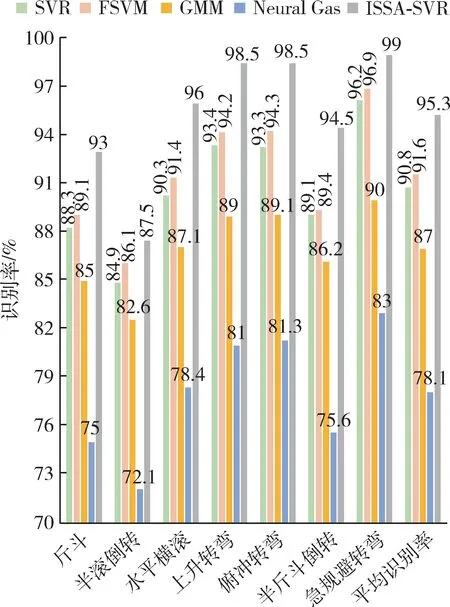
图4 5 种算法的复杂动作识别率Fig. 4 Complex action recognition rate of five algorithms

3.4 态势识别结果分析

根据图3，4 可以得出以下结论：

（1）对于简单的飞行动作，几种算法的识别率都非常高，识别率几乎接近100%，因为基本的飞行动作时间序列较为连贯，不易出现短时间内产生多个飞行片段的现象，ISSA-SVR 在识别基本动作时略好于其他几种算法。

（2）对于复杂的飞行动作，几种算法的识别率有所下降，这是因为复杂飞行动作的时间序列连贯性较高，在短时间内会有多个飞行片段，产生多个基本动作，在复杂的飞行动作下，由于SVR 会由ISSA 进行目标函数优化，得到的最优解远好于其他几种算法，识别率也有较大的提升。

（3）对于斤斗、半滚倒转、半斤斗倒转等动作的识别率相较其他复杂动作识别率偏低，是由于几种算法均采用的是线性核函数，对非线性的飞行动作识别率会有所降低。

4 结束语

针对传统算法识别飞机的飞行动作精确度低的问题，本文采用支持向量回归算法，解决了普通的支持向量机在处理多分类任务时出现不可分区域的问题，从而有效解决了飞行动作分类与回归的问题，在此基础上使用强化麻雀搜索算法优化了支持向量回归算法，使得支持向量回归算法的精确度有了一定的提升。仿真结果表明，ISSA-SVR 算法较SVR 算法、FSVM 算法、GMM 聚类算法以及神经网络算法在识别飞机飞行动作的准确率上有所提升，尤其是对复杂动作的识别率有大幅度的提升。