室内地埋供热管道泄漏的声学监测及其信号去噪方法研究1)

2024-03-16刘雅斌董燕京尹海全李昂峻丁志凌张宇宁

力学与实践 2024年1期

刘雅斌董燕京尹海全李昂峻丁志凌卢璇张宇宁,2)

*(北京市热力集团有限责任公司石景山分公司，北京 100028)

†(中国石油大学（北京）机械与储运工程学院，北京 102249)

管道漏损是目前室内地埋供热管道最为显著的安全问题，发生泄漏将造成资源浪费、室内建筑受损等不良影响[1-3]。因此，供热管道泄漏检测及精准定位漏点技术有着重要的工程意义。目前国内外用于管道漏损的检测方法主要包括负压波法、人工检巡、示踪法、红外法和声波法等。其中，声波法以其误报率低、操作简单、灵敏度高、成本较低、易于实现等优点已经在管道泄漏定位方面得到了较为广泛的应用[4]。然而，在采集到的声信号中，除了有泄漏信号外，还包括水在管道中流动的声信号和环境噪声。这些噪声频段对于管道漏损信号的分析将造成较大干扰。因此，对采集信号进行去噪有着重要的意义。

管道泄漏声信号为非平稳、非线性信号。对此类方法常用的信号去噪技术包括：小波阈值去噪[5]，经验模态函数分解（empirical mode decomposition,EMD）[6]，集合经验模态分解（ensemble empirical mode decomposition,EEMD）[7]和变分模态分解（variational mode decomposition,VMD）。小波阈值去噪[5]能够有效地对非平稳、非线性信号进行处理并且对于信号有着良好的自适应性，但其去噪效果很大程度上取决于小波基函数和层数的选取。郭晨城等[8]将改进的EMD 信号增强方法应用于管道泄漏检测中，信噪比提高可达16 dB，时延峰值更明显，漏点定位精度更高。孙立瑛等[9]针对管道泄漏声信号的非平稳特征，通过EMD 信号分析方法对声信号分解、重构，提取到泄漏声信号的本质特征，消除噪声信号的干扰。孟强等[10]使用EEMD和互谱分析对天然气管道泄漏点进行定位，利用EEMD 去除泄漏信号噪声并且利用互谱分析定位其特征频段，提高了漏点定位精度。

郑祥豪等[11]提出基于VMD 和互相关分析的旋转机械信号降噪研究方法，与EMD 和EEMD分解方法相比，基于VMD 分解法得到的降噪后信号含噪声更少，降噪效果更优。李帅永等[12]提出基于VMD 和互谱分析结合的低信噪比下的供水管道泄漏定位方法，并利用搭建的真实供水管道泄漏检测定位平台验证了该方法能够提高泄漏信号的信噪比，从而提高定位精度。吴珊珊等[13]针对供水管道中泄漏声信号的非平稳特征，提出基于相关系数的VMD 方法，结果表明VMD 分解方法在保留泄漏声信号本质特征的前提下，消除了噪声对信号的干扰。施晶等[14]针对水听器采集信号过程中外界噪声干扰问题，提出了一种基于VMD 和小波阈值的联合去噪方法，充分考虑了去噪信号和原始信号的相关性，使去噪信号保留了原始信号的重要信息。

综上，本文针对管道泄漏声信号非平稳、非线性的特征，提出一种利用VMD 提取模态分量、以排列熵作为筛选噪声信号的指标、利用改进小波软阈值去噪的方法。与以EMD 或EEMD 作为模态分量提取方法的去噪算法进行对比，计算结果表明，本文提出的去噪方法，排列熵最低，去噪效果最佳。

1 研究方法

1.1 VMD 分解原理

VMD 是一种可变尺度的信号分解方法，其具体步骤如下[11]。

VMD 将原始信号分解为k个本征模态函数（intrinsic mode function，IMF），将第k个IMF定义为一个有带宽限制的调幅-调频函数uk(t)，可表示为

式中，ϕk(t)为信号的相位，满足非单调递减的特性，即ϕk′(t)＞0 ；Ak(t)表示瞬时幅值且满足非负特性Ak(t)＞0 。

由约束变分条件得到

式中，{uk}={u1,u2,...,uk}和{ωk}={ω1,ω2,...,ωk}分别是所有模态以及其中心频率的集合；δ(t)为单位冲激函数；*为卷积运算。

通过引入拉格朗日乘子λ(t)和二次惩罚因子α，将上述约束变分问题转变为非约束变分问题，得到增广的拉格朗日函数，即

10月31日，EMW携手御鹿酒庄在广州圣丰索菲特酒店举行其第7场15周年品牌旗舰系列活动。现场邀请酒庄代表Marie-Emmanuelle Febvret及酒窖大师Pierre Boyer与大家一起品鉴来自大香槟区御鹿酒庄的经典干邑。在全球范围内，御鹿是干邑鉴赏家和侍酒师们公认的年份干邑行家。自1962年来，御鹿一直是英国女王伊丽莎白二世的唯一御用干邑，除它之外，再无任何干邑品牌被冠以“英国皇室认证”的殊荣。

式中，α为二次惩罚因子，λ(t)为拉格朗日乘子。

采用乘法算子交替方向法解决上述变分问题，最后通过傅里叶逆变换运算将频域转化为时域上的uk(t)。

1.2 排列熵

在信号分析过程中，信号的混乱或复杂程度可以通过排列熵值反映出来。排列熵值越小，信号越规则。排列熵值越大，信号越混沌。当排列熵值为0 时，信号内不存在混沌。当排列熵值达到1时，信号通常为白噪声。排列熵的基本原理如下[15]。

考虑任意离散信号x={xi,i=1,2,...,N}，将此信号进行空间重构为

式中，N是整个信号中的数据点总数，m为嵌入维数，τ为延迟时间。

将每个Xi内部按照递增顺序排序，即

原信号x={xi,i=1,2,...,N}的排列熵可表示为

归一化后的排列熵的变化范围为(0,1]，值越大表明信号所含信息越丰富，信号的复杂程度也越高，随机性越强。

1.3 改进小波软阈值降噪

此方法为在原有的小波软阈值去噪方法中，基于小波变换对不同层的小波系数进行处理[16]。在此，将不同层的小波系数替换为不同阶数的幂函数。其计算公式为

式中，IMFm(j)和IMFmk(j)分别是小波软阈值去噪之前和之后的IMF，j指IMF第j个数据点，m指第m阶IMF。

εm为IMF的m阶数据点阈值，其计算公式为

2 基于VMD 和排列熵的去噪方法

基于上述方法，本文提出的去噪方法的降噪流程如图1 所示，主要步骤如下。首先，将原始信号进行VMD 分解，得到若干IMFs。之后，根据排列熵准则来筛选有用IMFs 与噪声IMFs：设定排列熵阈值为0.3，低于阈值划分为有用的IMFs；将高于阈值的划分为噪声IMFs，将其使用改进小波软阈值方法去噪处理。最后，将两者进行重构，得到降噪后的信号。

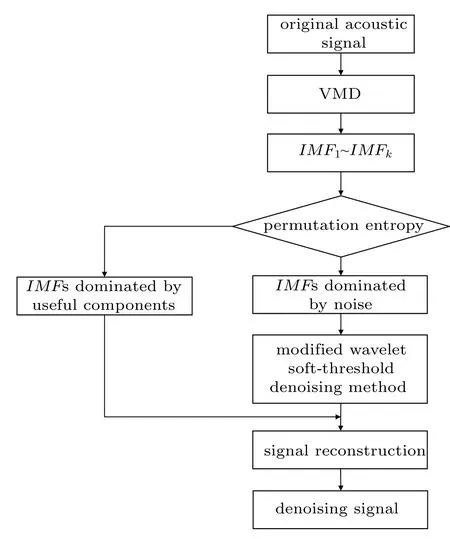
图1 基于 VMD 和排列熵的降噪流程图Fig.1 The flow chart of the denoising process based on VMD and permutation entropy

3 实测测点去噪研究

3.1 实验系统

本文搭建了户内埋地供热管道泄漏声信号检测实验系统，图2 为其示意图，主要包括供水循环系统、实验区域和声信号采集系统等。实验区域布置参考《城镇供热管网设计规范》（CJJ 34—2010）及户内地埋供热管常见施工布置，如图3 所示。实验中管道采用耐高温非交联聚乙烯管，管道外径2 cm，内径1.6 cm，在保温棉上整体呈S 型布置，泄漏点位于实验管道中间（图中红圈所示位置）。实验时在管道上方覆盖瓷砖，将拾音器（型号Ai800，测量范围20 Hz～20 kHz）分别放置在距离漏点5 cm 和40 cm 处，采集泄漏声信号。后续将声信号通过MATLAB 软件转化为数据，进行去噪处理。

图2 实验系统示意图Fig.2 The schematic diagram of the experimental system

图3 实验管段布置图Fig.3 The layout diagram of the experimental pipe section

3.2 数据样例

本文选取漏水孔径为2 mm，水流流量为3 L/min 时，拾音器分别在距离漏水点5 cm 和40 cm 处采集的声信号，信号采样频率设置为48 kHz。实测管道泄漏声信号的时域波形如图4 所示，图中纵轴S表示声信号的强度。对声信号进行快速傅里叶变换（fast Fourier transform，FFT）得到声信号频域波形图如图5 所示，图中纵轴A表示不同频率声信号所对应的幅值。对比可知，距漏水点不同距离处采集到的信号，特点为：两处信号的主频值相近，均为100 Hz 和300 Hz；当测点距离漏水点为5 cm 时的信号成分幅值较大，测点距离漏水点为40 cm 时的信号成分幅值较小。

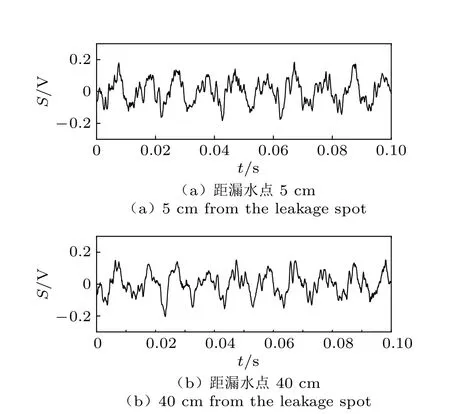
图4 距漏水点不同距离的实测管道泄漏声信号时域波形图Fig.4 The time domain waveform diagram of the measured pipe leakage sound signal at different distances from the leakage spot

图5 距漏水点不同距离的实测管道泄漏声信号频域波形图Fig.5 The frequency domain waveform diagram of the measured pipe leakage sound signal at different distances from the leakage spot

3.3 信号分解

对采集到的管道泄漏声信号分别进行EMD，EEMD 和VMD 分解，此处以距漏水点5 cm 的信号为例，得到分解后的分解时频图如图6～图8所示，其中(a)为IMFs 时域波形图，(b)为IMFs 频谱图。由图6 可以得到，原始信号经过EMD 分解成从高频到低频8 个IMF分量和1 个残余信号。在分解过程中存在模态混叠问题，如频率为300 Hz 的信号在IMF1～IMF4中都有出现。由图7 可以看到原始信号经过EEMD 分解分成高频到低频11 个IMFs 和1 个残余分量。高频噪声被很好地分离在IMF1～IMF3中，但在分离过程中仍然存在模态混叠问题，比如频率为100 Hz 的信号在IMF7和IMF8同时出现。在图8中可以得到，经过VMD 分解，原始信号分离成7 个IMF分量，模态混叠问题大幅度改善，有用的频率成分100 Hz 和300 Hz 被均匀分布在IMF1和IMF2中。对距离漏水点40 cm 的信号也使用3 种方法分解，其结果与距漏水点5 cm 的信号分解结果的规律相似，即相比于其他两种方法，VMD 解决模态混叠问题的效果更好。

图6 基于EMD 得到的实测管道泄漏声信号时频图Fig.6 The time-frequency diagram of the measured pipeline leakage acoustic signal based on EMD

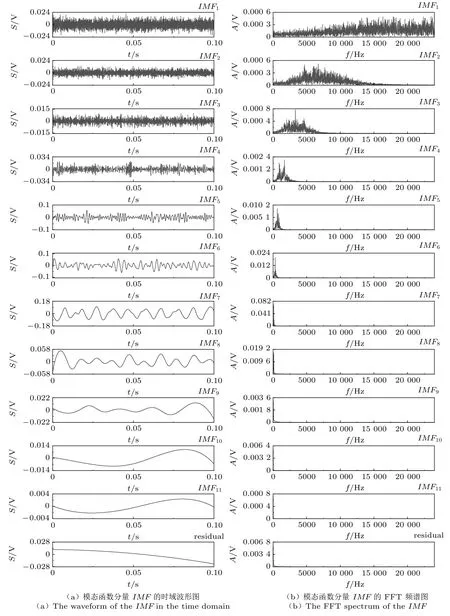
图7 基于EEMD 得到实测漏水管道声信号时频图Fig.7 The time-frequency diagram of the measured pipeline leakage acoustic signal based on EEMD

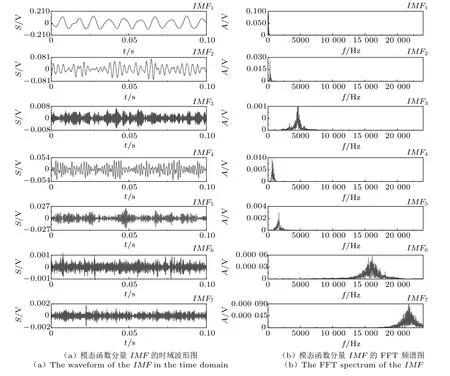
图8 基于VMD 得到的实测漏水管道声信号时频图Fig.8 The time-frequency diagram of the measured pipeline leakage acoustic signal based on VMD

4 去噪结果评价

分别计算距离漏水点5 cm 和40 cm 处实测信号经过EMD，EEMD 和VMD 分解后的IMFs的排列熵，结果如表1 所示。选取排列熵阈值0.3，将低于此阈值的IMFs 划分为有用IMFs，高于此阈值的IMFs 划分为噪声IMFs，将后者进行小波软阈值去噪处理。最后将有用IMFs、使用改进小波软阈值处理后的噪声IMFs 和残余信号进行重构。距漏水点5 cm 和40 cm 处的实测信号时域波形图，及其基于EMD，EEMD 和VMD去噪方法处理重构后的时域波形图，分别如图9和图10 所示。由图可知，基于VMD 去噪后的实测信号时域波形图最光滑、毛刺最少，而基于EMD 和EEMD 去噪后的实测信号时域波形图都存在部分不光滑的地方和毛刺（如图中画圈部分）。

表1 基于EMD/EEMD/VMD 得到的各IMF 的排列熵Table 1 The permutation entropy of each IMF based on EMD/EEMD/VMD

图9 基于EMD/EEMD/VMD 的距漏水点5 cm 实测管道泄漏声信号去噪结果Fig.9 The denoising results of pipeline leakage acoustic signal measured at 5 cm from leakage spot based on EMD/EEMD/VMD

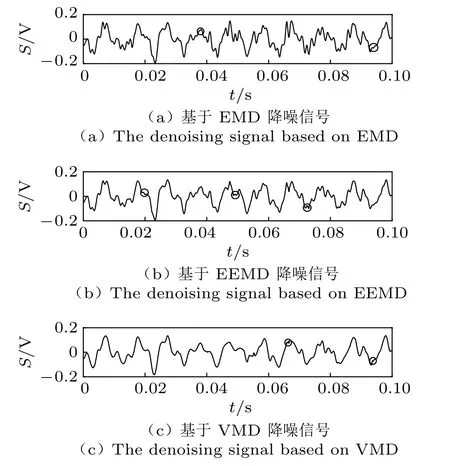
图10 基于EMD/EEMD/VMD 的距漏水点40 cm 实测管道泄漏声信号去噪结果Fig.10 The denoising results of pipeline leakage acoustic signal measured at 40 cm from the leakage spot based on EMD/EEMD/VMD

将图9 和图10 中通过不同方法去噪后的信号计算其排列熵，结果如表2 所列。由表可知，对于距离漏点5 cm 和40 cm 处采集的声信号，通过基于VMD 的去噪方法去噪后，相比基于EMD 和EEMD 的方法，其排列熵值最小。排列熵代表信号的混沌程度，其值越大，信号越混乱、随机性越强。因此，表中结果说明基于VMD 的去噪方法，能有效去除原始信号中的噪声成分，去噪效果最佳。

表2 基于EMD/EEMD/VMD 方法去噪后的实测管道泄漏声信号的排列熵Table 2 The average permutation entropy of pipeline leakage acoustic signals measured after denoising based on EMD/EEMD/VMD denoising method