交通载荷作用下埋地含缺陷玻璃钢管道力学行为研究1)

李振林 张笑影 刘 彤 于 晓 张 行,2) 董绍华

*(中国石油大学（北京）机械与储运工程学院，北京 102200)

†(中国石油大学（北京）管道技术与安全研究中心，北京 102200)

**(国家管网集团北京管道有限公司北京输油气分公司，北京 100101)

††(中国石油大学（北京）安全与海洋工程学院，北京 102200)

随着国内石油开采陆续进入高含水或特高含水阶段，油田采出液含水率逐年增高，常规金属管道失效问题日益严重，玻璃钢管道以耐腐蚀、寿命长等优点逐渐大量应用于油田埋地运输，由于现代复杂交通环境影响，埋地管道与道路交叉现象增多，地表交通载荷成为影响埋地管道安全运行的主要载荷之一，含缺陷埋地管道在承受地表交通载荷时相较于完整管道更易失效，对人民生命财产安全威胁更大[1-4]。

与常规金属管道和非金属聚乙烯等管道不同，玻璃钢管道是以环氧树脂和固化剂为基体材料，玻璃纤维为增强材料按照一定角度经连续缠绕、固化而成[5]，通过有限元模拟研究时需考虑管材为多层纤维缠绕的复合非线性材料。张济源等[6-7]通过实验和数值模拟研究了埋地玻璃钢管道在受车辆载荷下的管道轴向挠曲变形变化趋势。Lee 等[8]将实测埋地玻璃钢管道的横截面剖面挠度与Lowa公式及有限差分分析的预测结果进行了比较。魏连雨等[9]结合理论计算和实验，研究了车辆载荷作用下埋地玻璃钢夹砂管的受力变形特性。Sun 等[10]通过测试研究了恒定载荷和恒定位移条件下的玻璃钢夹砂管道环刚度随时间的变化规律。以上研究中，关于埋地玻璃钢管道受载荷作用的力学响应研究主要集中于完整管道轴向变形及截面挠度与环刚度的研究，对于含缺陷埋地玻璃钢管道有限元模拟及管材缠绕层的模拟研究分析较少。本文主要考虑了玻璃钢管道各向异性管材及各缠绕层不同角度，基于有限元仿真软件ABAQUS建立了含不同形状沟槽型缺陷埋地玻璃钢管道模型，分析不同埋深工况及不同形状缺陷对管道各层中截面沿环向等效应力分布规律的影响。

1 有限元模型

1.1 材料属性及参数

土体模型采用能够反映土摩擦性材料特性的Mohr-Coulomb 弹塑性模型。利用ABAQUS 软件内置的弹塑性模块模拟，弹性通过给定弹性模量E和泊松比ν定义各向同性线性弹性，其应力-应变关系如式（1）所示；塑性采用适用于材料各向同性硬化的Mohr-Coulomb 塑性模型，其Mohr-Coulomb 屈服准则控制方程为

式中，σij(i,j=1,2,3)为应力张量分量；εij(i,j=1,2,3)为应变张量分量；σ1，σ2和σ3分别表示第一、第二和第三主应力；c和ϕ分别表示黏聚力和内摩擦角。Mohr-Coulomb 准则假定在材料中的任意点上，当切应力达到与相同平面内法向切应力线性相关的值时，发生屈服。设置地表硬质土、埋地回填土及地基土三层埋地土体模型，其参数[11-12]见表1。

表1 土壤模型材料参数Table 1 Soil model material parameters

玻璃钢管道管材主要由环氧树脂基体和无碱增强玻璃纤维经过连续缠绕、固化而成，属于典型正交各向异性纤维增强复合材料，与各向同性均质材料不同，各向异性六面体单元各面上的应力代表该单元的应力状态[11]，如图1 所示。

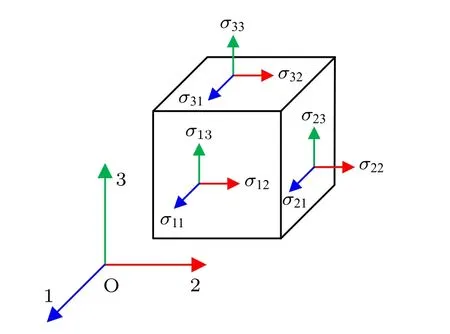
图1 各向异性六面体应力Fig.1 Stress of anisotropic hexahedron

在对各向异性复合材料仿真模拟研究时通常采用工程常数的方式或者直接指定弹性刚度矩阵来定义材料响应，主要包括：3 个与材料主方向关联的模量E1，E2和E3；泊松比µ12，µ13和µ23；剪切模量G12，G13和G23，并根据式（4）定义弹性柔量。本文选用玻璃钢管道材料工程常数[13-14]见表2。

表2 玻璃纤维增强环氧树脂基体复合材料工程常数Table 2 Engineering constants of glass fiber reinforced epoxy resin matrix composites

1.2 有限元模型建立

埋土模型依据国内某油田实际运行情况选择埋深1.0～2.5 m，玻璃钢管道模型取长1.0 m，外径110 mm，壁厚5 mm，埋土模型整体长大于6 倍管径，取4.0 m，宽与管道长度一致，取1.0 m，地表硬质土层0.1 m，地基层1.0 m。

由于交通载荷是一种复杂随机动载荷，实现完全真实模拟较困难，在道路地面设计规范中一般将其简化为静止的集中点源、线源（线状均布）或面源（圆形面分布）载荷，本文研究对象主要为埋地玻璃钢管道管体，因此选取交通载荷以静止面源均匀载荷的形式施加。真实的车轮与路面的接触面积近似为椭圆形，并认为车辆轴载在接触面积上均匀分布，以单个车轮轮胎作用为例，将车轮接触面积进一步简化为一个当量矩形，如图2 所示。

图2 载荷作用区简化示意图Fig.2 Simplified diagram of load area

单轮接地面积近似为0.4L×0.6L矩形与两个半径为0.3L半圆形组合，接触面积为

取胎压为P=0.7 MPa，选取双轮组单轴标准轴载100 kN，单轮载荷F，则有

同时可知

联立各式可得：0.6L=0.156 m，L2=0.23 m，即轮胎接地面积简化为0.23 m×0.156 m 矩形区[15]，整体模型载荷作用示意如图3 所示。

图3 整体模型载荷作用示意图（单位：m）Fig.3 Schematic diagram of load action of the overall model (unit: m)

埋地管道不可避免地会因多种原因产生局部体积型缺陷，深度可达到壁厚10%[16]，由于实际缺陷形状复杂，实现完全真实模拟较困难，考虑主要缺陷影响因素，通过仿真模拟研究时许多研究者将管体缺陷进行简化处理[12,17-18]，本文将管体缺陷简化为规则矩形沟槽，以管体轴向中部环向顶部为0°位置，相对应管体底部为180°位置建立深度为壁厚10%缺陷管道模型。设置轴向、环向和轴向与环向组合缺陷，不同形状沟槽型缺陷如图4 所示。设计不同管道埋深工况1.0 m，1.5 m，2.0 m 和2.5 m，管道运行内压10 MPa。

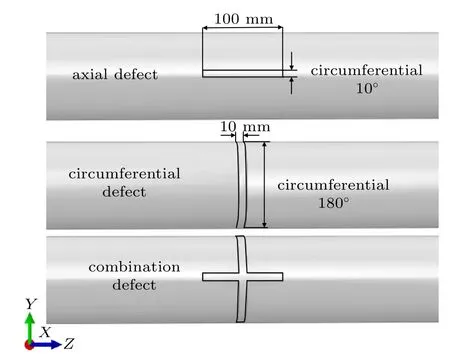
图4 管道缺陷示意图Fig.4 Schematic diagram of pipeline defect types

对于各向异性复合材料通常借助层合板理论研究其力学行为[19]。本文所建玻璃钢管道模型采用层合板模块创建玻璃钢管道实体复合层模型，设置管体沿壁厚以内层为第一层均匀切分10 个连续壳复合层，并对每个复合层赋工程常数材料属性，厚度积分规则选用Simpson，以管道轴向为法线方向建立表面离散坐标系，通过设置不同层合板角度模拟玻璃纤维缠绕方向，隔层缠绕角度为 ±55°[20-21]，各缠绕层沿法向堆叠。不同复合层缠绕角度及堆叠方向如图5 所示，图中不同方向1，2 平面旋转角度表示材料不同缠绕方向，各层堆叠方向S 与法线方向3 相同。

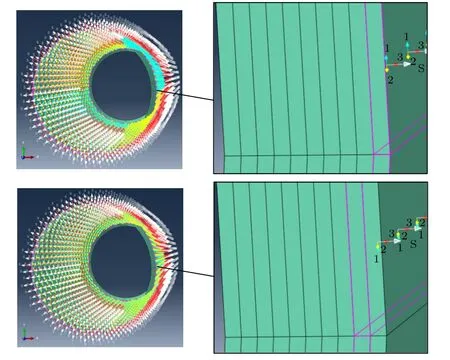
图5 不同复合层材料缠绕角度及堆叠方向Fig.5 Winding angles and stacking directions of different composite layers

初始边界条件设置土体模型底面完全固结，上表面无约束，前后面设置约束Z方向位移，两侧面约束X方向位移，管道模型两轴端设置约束轴向（Z方向）位移，整体模型边界条件设置如图6 所示。管道外表面与土壤内表面设置面-面非线性接触，整体模型施加重力载荷模拟埋土与管道自重，埋土模型网格单元类型C3D8R 单元为八节点六面体线性缩减积分实体单元，玻璃钢管道模型网格采用线性六面体缩减积分八节点四边形面内通用连续壳SC8R 扫掠划分模拟，并逐层逐部定义各复合层扫掠方向与层合板堆叠方向相同。

图6 整体模型边界条件设置Fig.6 Setting of boundary conditions of the overall model

对整体模型进行网格无关性分析，不同网格密度管体中部管顶0°位置von Mises 应力随分析步时间变化曲线如图7 所示，分析可知，随网格数量增加，曲线基本保持一致，整体模型对网格敏感性较低。当整体模型网格数量超过228 321后应力变化趋于稳定，从228 321 网格数到245 313网格数与245 313 网格数到276 633 网格数最大应力相差均小于0.01%。对管道模型与埋土模型载荷作用区做网格加密处理，整体模型网格数为228 321，整体有限元模型网格划分如图8 所示。

图7 不同网格密度管顶位置应力变化Fig.7 Change of stress at top position of tube with different mesh densities

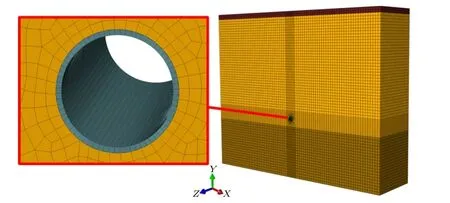
图8 整体模型网格划分Fig.8 Mesh division of the overall model

2 结果与分析

2.1 埋深与缺陷影响

沿管道轴向中部位置切分管道，不同埋深工况下无缺陷管道中截面各层沿环向von Mises 应力分布如图9 所示，分析可知，不同埋深下的无缺陷管道中部截面沿环向应力分布规律一致，各层应力分布均匀，管道在0°及180°位置各层均有局部应力集中现象但影响较小。其中埋深1.0 m 工况下管道各层环向应力均大于其他埋深工况，管道整体环向应力峰值位于管道最内层，为116.56 MPa。

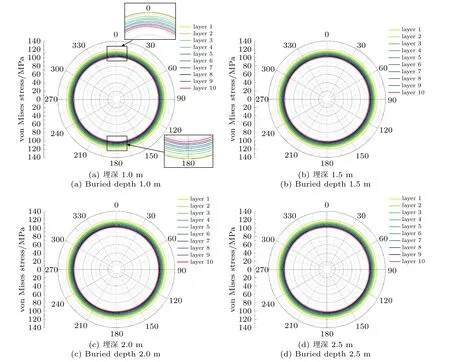
图9 无缺陷管道中截面各层沿环向应力分布Fig.9 Distribution of circumferential stress in each layer of the section of faultless pipeline

不同埋深工况下含轴向缺陷管道中截面各层沿环向应力分布如图10 所示。分析可知，不同埋深工况下管道应力分布规律一致。管道顶部0°位置有明显应力突变现象，各层应力关于缺陷中轴线呈对称分布。管道内区域（第1～3 层）0°位置相对于其他位置应力呈减小趋势，管道中区域（第4，5 层）各处应力相对均匀，外区域（第6～9 层）0°位置相对于其他位置应力呈增大趋势，其中第8 层突变幅度与应力峰值均为所有层中最高，埋深对突变幅度及应力峰值影响较小。

图10 含轴向缺陷管道中截面各层沿环向应力分布Fig.10 Distribution of circumferential stress in each layer of the section of the pipeline with axial defects

不同埋深工况下含环向缺陷管道中截面各层沿环向应力分布如图11 所示。分析可知，不同埋深工况下管道应力分布规律一致。含缺陷区间（90°与270°上半部）在90°与270°缺陷过渡位置管道外区域各层应力发生突变，其中第8 层和第9 层突变幅值明显大于其他各层。

图11 含环向缺陷管道中截面各层沿环向应力分布Fig.11 Distribution of circumferential stress in each layer of the section of pipeline with circumferential defects

不同埋深工况下含组合缺陷管道中截面各层沿环向应力如图12 所示。分析可知，不同埋深工况下管道应力分布规律一致。90°与270°位置应力变化规律与仅含环向缺陷管道应力分布规律一致，第8 层和第9 层突变幅值明显大于其他各层。与仅含环向缺陷相比，组合缺陷管道应力突变区间更大；与仅含轴向缺陷不同，组合缺陷管道0°位置只有最内层（第1 层）应力呈下降趋势，其他各层应力均呈增大趋势。

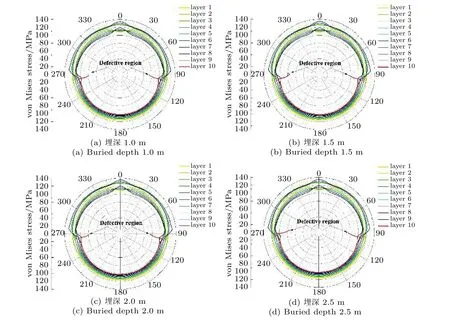
图12 含组合缺陷管道中截面各层沿环向应力分布Fig.12 Distribution of circumferential stress in each layer of cross section of pipeline with combined defects

不同埋深工况下，管道0°与90°位置沿径向各层应力变化曲线如图13 所示，以埋深1.0 m 为例，含缺陷管道内外层区域应力云图如图14 所示。

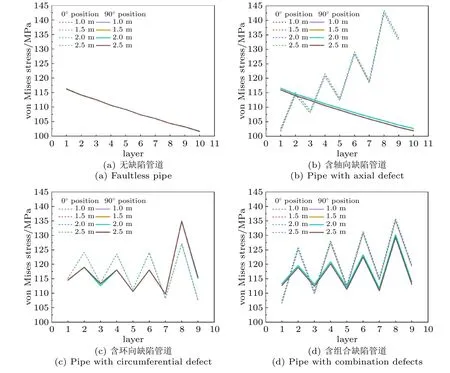
图13 含缺陷管道0°与90°位置沿径向应力分布Fig.13 The stress distribution along the radial direction at 0° and 90° of the pipe with defects

图14 含缺陷管道内外层区域应力云图：(a)轴向缺陷第2 层；(b)轴向缺陷第8 层；(c)环向缺陷第1 层；(d)环向缺陷第7 层；(e)组合缺陷第3 层；(f)组合缺陷第6 层Fig.14 Stress nephogram of inner and outer layers of pipelines with defects (a)the second layer of axial defects;(b)the eighth layer of axial defects;(c)the first layer of circumferential defects;(d)the seventh layer of circumferential defects;(e)the third layer of combined defects and (f)the sixth layer of combined defects

分析可知，管道无缺陷区域各层应力由内层向外层递减，如图13(a)和13(b)90°位置。含轴向缺陷管道0°位置沿径向各层应力呈增大趋势，相邻层间缠绕角度为-55°层应力大于+55°层。相同缠绕角度层间管道外区域层应力大于内区域层，如图13(b)0°位置缠绕角度为-55°的第2 层与第8 层，结合图14(a)和图14(b)分析可知，管道内区域应力主要沿缠绕方向即图中离散坐标系方向1 集中于缺陷外周对称角处，外区域应力主要集中于缺陷内区。

含环向缺陷管道缠绕角度为+55°各层应力沿径向方向递减。管道内区域缠绕角度+55°层0°与90°位置应力接近，外区域层0°位置应力小于90°位置，如图13(c)缠绕角度为+55°的第1 层与第7 层，结合图14(c)和图14(d)分析可知，管道内区域应力主要集中于缺陷外周对称角处，外区域应力主要集中于缺陷内区90°与270°位置。

含组合缺陷管道与含环向缺陷管道不同，缠绕角度为+55°各层应力沿径向方向递增。缠绕角度为+55°层内区域0°位置应力小于90°位置，缠绕角度为-55°层内外区域0°位置应力均大于90°位置，如图13(d)缠绕角度为-55°的第3 层与缠绕角度为+55°的第6 层，结合图14(e)和图14(f)分析可知，内区域应力集中于缺陷外周角处，外区域应力集中于缺陷内区管顶0°位置。

结合不同缺陷不同埋深工况分析可知，相较于埋深，缺陷对管道中截面各层沿环向应力分布规律影响较大。管道无缺陷时整体应力分布均匀，由内层向外层递减，这表明无缺陷管道在内压、土壤及地表载荷共同作用下，内压作用对管道的应力影响最大；管道仅含轴向缺陷时，管顶0°位置应力发生突变，且越接近管道最外层应力突变越明显；管道仅含环向缺陷时，应力分布以90°和270°缺陷临界位置为转变点；管道含组合缺陷时，会影响管道内外区域在0°位置的应力分布变化趋势，增大90°与270°位置的应力突变区间；不同埋深工况下含缺陷管道内层区域应力集中于缺陷外周对角，外层区域集中于缺陷内区。

2.2 地表交通载荷影响

以埋深1.0 m 工况下含轴向缺陷管道为例，研究不同地表交通载荷对无内压含缺陷管道应力分布规律的影响，不同载荷作用下含轴向缺陷管道第8 层中截面沿环向不同位置应力分布如图15所示，分析可知，不同载荷作用下管道应力分布规律一致，管顶0°与管底180°位置应力大于管道圆周两侧90°和270°位置应力，各位置应力与地表载荷呈正相关。地表载荷对管顶0°位置应力影响最大，0 MPa 到2.1 MPa 增幅为8%，对管底180°位置应力影响最小，0 MPa 到2.1 MPa 增幅小于1%。

图15 含轴向缺陷管道中截面沿环向不同位置应力分布Fig.15 The stress distribution of the section of the pipeline with axial defects along the circumferential direction

2.3 缺陷深度影响

以埋深1.0 m 工况下含轴向缺陷管道为例，含不同相对深度缺陷管道中截面沿环向应力分布如图16 所示，不同相对深度缺陷管道内外区域应力云图如图17 所示。分析可知，含不同相对深度缺陷的管道中截面沿环向应力分布规律一致。管道不同层区域应力相对于缺陷中轴线呈对称分布，缺陷相对深度越大管道应力与缺陷位置处的应力突变幅度越大。含缺陷部分管道内层区域应力峰值位于缺陷边缘，外层区域应力峰值位于缺陷中部即管顶0°位置处。缺陷深度对管道内外层应力集中区域分布规律影响较小，管道内层区域应力沿缠绕方向集中于缺陷外周对角处，外层区域应力集中于缺陷内区且以缺陷中轴线对称分布，越接近缺陷中部位置应力集中越明显。

图16 含不同深度缺陷管道中截面各层沿环向应力分布Fig.16 Circumferential stress distribution of the sections of pipelines with different depth defects

图17 不同深度缺陷管道内外层区域应力云图：(a)相对深度15%第3 层；(b)相对深度15%第9 层；(c)相对深度20%第3 层；(d)相对深度20%第8 层；(e)相对深度30%第3 层；(f)相对深度30%第7 层Fig.17 Stress nephogram of inner and outer layers of pipelines with defects of different depths: (a)the third layer with a relative depth of 15%;(b)the ninth layer with a relative depth of 15%;(c)the third layer with a relative depth of 20%;(d)the eighth layer with a relative depth of 20%;(e)the third layer with a relative depth of 30% and (f)the seventh layer with a relative depth of 30%

2.4 影响因素分析

根据仿真结果对不同工况下玻璃钢管道力学演化规律进行分析，不同埋深不同缺陷管道第8层中截面沿环向应力突变幅度见表3，应力峰值见表4。分析可知，无缺陷管道应力均匀且峰值较小，管道仅含轴向缺陷时应力突变幅度与应力峰值均大于含其他形状缺陷管道。这表明，在内压、土壤及地表载荷作用下管道无缺陷时处于最安全工况，管道仅含轴向缺陷时更易发生失效。分析轴向缺陷深度对管道最大应力影响，含不同相对深度轴向缺陷管道最内、外层应力峰值见图18，分析可知，管道内外层应力随缺陷深度增加而增大，缺陷深度对管道外层应力峰值影响较大，当缺陷相对深度大于10%时管道内外层应力峰值差值明显增大，缺陷相对深度由10%增至15%和25%增至30%时，管道外层应力峰值增大速率明显大于其他缺陷相对深度，这表明当缺陷深度大于10%时管道最外层相较于内层更易发生层连锁失效。

图18 含不同相对深度缺陷管道应力峰值Fig.18 Stress peak in pipelines with defects of different relative depths

表3 不同埋深与不同缺陷管道第8 层应力突变幅度（单位：%）Table 3 Stress mutation amplitude in the 8th layer of pipelines with different buried depths and defects（unit：%）

表4 不同埋深与不同缺陷管道第8 层应力峰值（单位：MPa）Table 4 Stress peak in the 8th layer of pipelines with different buried depths and defects (unit: MPa)

3 结论

采用工程常数定义材料响应并结合层合板模型模拟正交各向异性复合玻璃钢管材，建立了含不同形状沟槽型缺陷管道模型和不同埋深管土模型，并对地表交通载荷、土壤及管道内压共同作用下的玻璃钢管道中截面沿环向应力分布规律与影响因素进行了分析，结果表明如下。

（1）影响因素中不同形状缺陷对玻璃钢管道应力分布规律影响最大，其中管道仅含轴向缺陷时管体应力峰值与应力突变幅度最大，更易发生失效。

（2）缺陷会使管道出现应力突变与应力集中，管道内层区域应力沿管材缠绕方向集中于缺陷对称角处，外层区域应力集中于缺陷区域且相对于缺陷中轴线呈对称分布，管道整体应力突变及应力峰值位于外区域缺陷外层。与含其他缺陷类型管道相比，组合缺陷会影响管道内外区域在0°位置的应力分布变化趋势，增大90°与270°位置的应力突变区间。

（3）地表交通载荷作用对含内压管道中截面沿环向应力分布影响较小，对无内压管道管顶0°位置应力影响最大。缺陷相对深度对管道沿环向应力峰值影响较大，随相对深度的增加应力增大，当相对深度大于10%时管道内外区域层应力差值增大且最外层应力大于内层应力，外层缺陷处易发生缺陷层连锁失效。