椭球体绕流阻力数值模拟研究1)

周 锟 张 权

(武汉科技大学省部共建耐火材料与冶金国家重点实验室，武汉 430081)

颗粒在无界均匀流场中定常运动时所受的流体作用力是最基本的流体力学问题之一[1-2]，这是考虑更复杂的颗粒与边界或者颗粒之间相互作用的基础。即便不考虑空间不均匀及时间非定常等效应，单一的圆球其所受的作用力也均呈现出足够丰富的形态[3]。圆球受力主要是沿与流体相对运动方向一致的阻力，而当绕过圆球的尾流变得不稳定时，也会产生侧向力，但侧向力在量级上要小于阻力。在极小雷诺数（Re=ρDU/µ，ρ为流体密度，D为圆球直径，U为流体与圆球相对速度，µ为流体动力黏性）下，理论解析结果表明圆球阻力与来流相对速度成正比。在较大雷诺数下，圆球阻力常用沉降法来测定，即在静止流体中让圆球沉降，以达到稳定的沉降速度。此时，圆球重力与阻力达到平衡，便可以通过圆球的重力来计算出对应于沉降速度的阻力系数，即Cd=2G/(ρAU2)，式 中G为 重力，A为 截面积，U为最终的沉降速度。即便原理上如此简单的测定方法，其结果仍然存在诸多不确定性，比如圆球常常并不是垂直沉降，而是呈现横向漂移，故而难以精确判定其真正的沉降速度，或者圆球存在一定的旋转速度，从而偏离了理想设定。正是由于圆球阻力的基本性以及复杂性，已经有大量的相关研究工作提出多种经验关系式来表征圆球阻力系数与雷诺数之间的关系[4-5]。圆球阻力系数与雷诺数之间的关系常常被绘制成图形，称为标准阻力曲线。此曲线据称是工程流体力学中应用第二广泛的图线[6]。浸没物体的阻力由两部分组成，即形状阻力与黏性阻力。形状阻力由物体前后缘的压力差决定，也被称为压差阻力。物体在垂直来流方向的迎风面积对形状阻力有着决定性的作用。黏性阻力主要决定于物体平行于来流方向的表面受到的黏性剪切力，而剪切率可近似认为正比于来流速度，所以黏性阻力大体上与来流速度呈正比关系。对于圆球而言，在雷诺数Re →0条件下，形状阻力与黏性阻力之比为1∶2。而随着雷诺数的增大，两者之比不断增大。当雷诺数增大到牛顿阻力区时(Re ＞1000)，黏性阻力在总阻力中的占比很小，总阻力基本由形状阻力决定，而此时阻力系数基本稳定，约为0.43。圆球阻力系数从Stokes 阻力到牛顿阻力之间的变化规律，可以从黏性阻力与形状阻力对速度的依赖性进行定性分析。在雷诺数很小时，黏性阻力与形状阻力都与来流速度成正比关系。随着雷诺数增大，流动控制方程中的非线性对流项作用不断增加，形状阻力开始正比于速度平方（这一点可以从伯努利原理看出），从而使得阻力系数渐渐稳定下来，不再变化（因为阻力系数的定义包含速度平方项）。牛顿阻力系数为0.43可以理解为流向圆球迎风面的流体中，有大约43%的流体受到圆球的阻碍而完全停止下来，其余流体绕过圆球，仍然保持原来速度行进。笔者认为，这种简单直观的方式（但原理上不完全正确），有助于加深对形状阻力的理解（一种更正确但较为复杂的方式则是考虑均匀流、源、尾流射流等的叠加[7]）。

工程及自然界颗粒多相流中，颗粒基本上都是非球形。由于非球颗粒本身形状的多样性以及其阻力对方向显著的依赖性，使得非球形颗粒的受力更加复杂。Haider 等[8]在这方面做出了开创性的工作，通过分析拟合已知的实验数据，首次给出了对于任意形状颗粒的阻力经验公式。之后，便有一批学者提出各种修正改进的经验公式[8-16]。在2.4 节，将对多种流行的经验公式原理及精度进行较详细讨论。对于非球颗粒的阻力，有几条一般性的结论值得关注。当颗粒雷诺数（以等体积球体直径作为特征尺度定义）接近零时，Hill 等[17]证明一个颗粒的Stokes 阻力小于任意形状的外包颗粒，而大于任意形状的内含颗粒。此结论结合已知的任意椭球阻力理论解[4]，可以用来估计任意形状颗粒的Stokes 阻力，亦即使用此颗粒的最小外包与最大内含椭球阻力来估计阻力上限与下限，而将上限与下限的平均作为其估计阻力。大量实验数据表明[18]，在较小雷诺数条件下，不论是扁平或细长的颗粒，无论其在流场中是横向或直向放置，其所受的阻力都比同体积的等轴颗粒（如圆球、正方块等）要大。这是因为低雷诺数下黏性阻力在总阻力中的占比较大，而形状阻力与黏性阻力在颗粒的不同取向条件下，存在此消彼长的关系，使得总阻力基本恒定。当扁平或细长颗粒以较小迎风面置于流场中，其形状阻力较小，然而此时平行于流动方向的表面积增大，从而使得黏性阻力上升；反之亦然。而随着雷诺数不断增大，黏性阻力的占比不断减小，总阻力则基本上由形状阻力决定。此时，扁平或细长的颗粒以较小迎风面“顺”置于流场中时，其阻力显著小于圆球；而当其“横”置时，阻力则显著大于圆球。如果对所有空间取向结果进行平均后，非球颗粒的平均阻力一般大于圆球，即圆球平均意义上具有最小阻力[13]。

本文通过数值模拟来研究椭球体绕流的阻力问题，其主要意义有以下四点。（1）模拟采用高阶的谱元方法[19]，此方法结合了谱方法的数值高精度与有限元法的几何灵活性等优点。目前，谱元法的应用还相对较少，因而本文有一定的数值实践意义。（2）在实验研究方面，对非球颗粒的阻力测定主要采用自由沉降法，但沉降法中给出的是颗粒各种空间取向概率平均后的结果，无法给出颗粒特定方向的阻力。尽管概率平均后的阻力结果更加具有“实践”意义，但从模型角度而言，其增加了不确定性。就如当前流行的点颗粒（point-particle）模拟方法[20]，其要求颗粒的阻力模型尽可能精确且“纯粹”。而本文将具体研究不同空间取向（亦即来流攻角）的椭球阻力，这是一般沉降实验无法提供的结果。（3）数值模拟将量化颗粒总阻力中形状阻力与黏性阻力的构成比例，这也是大多实验结果中所缺乏的。（4）通过对比数值模拟结果与各种流行经验公式的预估，从而系统评价不同经验公式的精度及适用性等。本文的结构如下：第1 节介绍数值模拟的基本内容；第2 节为结果与分析：扁平到细长椭球的阻力（圆球为特例）对雷诺数与来流攻角的依赖性；形状阻力与黏性阻力的比例；不同攻角下的流动结构；数值结果与多种经验公式的对比分析。第3 节是结论。

1 模型与方法

1.1 槽道流动模型

本文数值模拟采用经典的槽道流动模型，将椭球体置于槽道中心，而让流体稳定流过椭球体，模拟了在不同来流速度，多种椭球体形状，以及各种流动攻角条件下椭球体所受的阻力。槽道采用均匀速度入口条件，壁面为滑移边界，以入口同样速度运动，亦即无切应力边界条件；出口使用自然出流条件，即垂直方向速度梯度为零。

此处，椭球体特指回转椭球体，具有一个对称回转轴。其形状由平行及垂直于对称轴的两个极径所确定。椭球体的长径比Ar定义为两极径的比值（平行/垂直），Ar ＞1 表示细长的椭球体，Ar →∞极限为针状体；Ar ＜1 表示扁平的椭球体，Ar →0 极限为无厚度圆盘；Ar=1则对应于圆球。本文模拟中考虑了Ar=0.25,0.5,1,2,4,8等6 种工况。

为了比较不同长径比，任意空间取向椭球体的受力问题，这里采用惯常的等效直径De，即等体积圆球的直径来作为椭球体的特征长度。相应地，颗粒雷诺数定义为Re=U∞De/ν，其中U∞表示槽道入口来流速度，ν为流体运动黏性。文中模拟的雷诺数为Re=0.1,1,10,100,1000等5 种工况。最小值选取Re=0.1 是为了比较数值模拟结果与已知的Stokes 流动理论解；而最大值选取Re=1000 则出于3 种考虑：首先，对于圆球而言，Re=1000 已经开始进入牛顿阻力区，即圆球阻力系数基本不随雷诺数变化；再者，对于工程中大多颗粒多相流动而言，其颗粒雷诺数最大就约为103量级；最后，对于直接数值模拟而言，计算量正比于Re3，这意味着由于计算资源的限制，无法实质性提升所能模拟的雷诺数范围。本文模拟使用云计算服务器进行，约消耗4万机时。如若将模拟的最大雷诺数提升10 倍，那么需要将计算量提升1000 倍至4000 万机时，这对于笔者而言是不可能的任务。

椭球体的受力与其空间取向紧密相关。这里，采用椭球回转轴与来流之间的夹角ϕ来描述其空间取向。值得特别说明的是，因为槽道采用直角坐标系来描述，而置于槽道中心的椭球体需要两个角度参数来唯一确定其在槽道内的空间取向——这一事实有时引起误解，认为需要两个角度参数来描述椭球体与来流之间的夹角关系。事实上，因为回转对称性，来流方向与回转轴之间只需要一个角度参数来描述。在槽道模型上“需要”的两个角度参数，其中一个角度是冗余的，只需考虑夹角ϕ在0～90°之间的变化，就已经包含椭球与来流之间所有的取向。这里，使用x轴表示流动方向，夹角ϕ位于x-y平面内。当ϕ=0°表示回转轴与流动方向一致；而ϕ=90°表示回转轴与流动方向垂直。本文模拟考虑了ϕ=0°,15°,30°,45°,60°,75°,90°等7 种工况。

上面介绍了本文模拟中涉及的3 个参数Ar，Re，以及ϕ。这些工况的组合共有约6×5×7=210 种（其中Ar=1 对应于球体，其不涉及空间取向ϕ）。

1.2 模拟方法

本文目标是对多种长径比椭球在各种空间取向下的阻力问题进行高精度的直接数值模拟。因为几何模型的相对复杂性，高精度的谱方法不能很好地来处理此问题。这里，采用兼具高精度以及几何适应性的谱元法来进行模拟。

谱元法[19]可以看成是谱方法与有限元方法的结合体。传统谱方法是采用特定的正交基函数叠加来表征流场。正交基函数的选取，需要考虑流场的边界条件，使得每个基函数都自动满足。而在一般的加权余量法框架下来离散控制方程，得到关于基函数的未知系数的代数方程组。通过求解此方程组，得到系数，从而得到流场数值解。在各种流行的计算流体力学方法中，谱方法对于光滑流场具有最高的数值精度与效率。然而，对于复杂的流动区域，则无法找到合适的基函数，使得谱方法的应用仅限制于简单的几何区域。有限元方法则首先对几何计算区域进行单元划分，而划分单元常常是简单的几何体，比如三角形，四边形（二维）或者四面体，六面体（三维）；然后，对于单个的单元，选取基函数来逼近此单元内的流场。不同单元之间的边界处，满足协同性条件，即在边界上流场是连续的（甚至具有一定的光滑性——针对某些方法而言）。提升有限元方法的精度有两种方式，即所谓的h 型与p 型。h 型就是采用细密的离散单元；而p 型则是在单元内采用更高阶的逼近函数。相对谱方法而言，有限元方法具有极大的几何区域适应性。而谱元法，则结合谱方法与有限元。首先，使用六面体网格对三维流场进行离散，如同有限元方法中的有限元划分；然后，在每个单元体内，采用高阶的谱函数进行逼近。而不同单元之间，只需满足在交界面上的速度连续性条件，除此之处，对单元之间的相互拓扑关系没有要求。简言之，谱元法中的网格离散为局部结构化，而全局非结构化。本文模拟中单元体内采用七阶方法进行逼近。前期研究[21]表明高阶方法在模拟表面黏性力问题上相对低阶方法有极其显著的精度优势。此处的谱元方法的实现采用开源代码Nek5000[22]。

1.3 网格离散

数值模拟的精度取决于两方面：离散格式以及网格尺寸。在1.2 中介绍了本文模拟采用的高阶格式，这里说明如何生成与高阶格式匹配的高质量网格。对于绕流问题，六面体型的贴体网格具有最佳质量。为了精确模拟颗粒表面的黏性摩擦力，近壁网格必需位于边界层的黏性底层内[21]，这就要求近壁网格尺寸正比于，即网格尺寸随着雷诺数增大而相应地减小。对于Re=1000的问题，近壁网格尺寸约为0.01De。对于较小雷诺数，网格尺寸相应地放大来节约计算资源。

为了减小槽道尺寸对模拟结果的影响，要求槽道尽可能“大”。在前期研究[21]中，从理论及数值模拟两方向详细讨论了槽道尺寸的影响。这里依照之前的研究结果，对于Re为0.1,1,10 等3 种雷诺数，槽道尺寸选取为100De；对于Re为100,1000等两种雷诺数，槽道尺寸选取为40De。值得特别指出的是，这里，槽道采用方型结构，并且对于小雷诺数流动，槽道尺寸更大，而大雷诺数流动，槽道尺寸反而较小。这不同于惯常的槽道流动模拟形状与尺寸设置，而是为了取得更好的计算效率与更小的槽道边界影响。

网格从近壁开始，向外不断拉升，形成O 型网格包裹椭球体（如图1）。值得特别指出的是，传统的O 型网格划分方法（如图1(a)），对于圆球形状不存在困难，但对于倾斜的细长椭球体，在其尖端存在极大的困难（如图1(b)）。这是因为O 型网格的拓扑关系需要将椭球表面划分成六块，与六面体的槽道形成对应关系，这六组一一对应的表面应该大体平行，否则将会造成离散的六面体网格畸变严重，乃至近壁面网格相互交叉穿越，使得模拟无法进行（谱元法要求每个网格单元可以仿射至规则的六面体）。为了解决传统O 型网格所面临的困难，这里采用重叠网格方法来离散。在六面体的槽道与椭球体之间，使用一个球面进行分割，在槽道与球面，球面与椭球之间分别生成O 型网格（如图1(c)，图1(d)所示）。这两套网格相互独立，从而避免了倾斜椭球体O型网格生成过程中的畸变或者交叉问题。使用重叠网格，则需要计算方法进行相应的调整，在重叠网格区域进行模拟结果的协调插值。这原本是复杂的计算方法，可能带来数值稳定性、精度等多方面问题。在本文研究中，将重叠网格区域置于离椭球体足够远的空间位置，这样无论是速度场或者压力场，在重叠区域都是非常缓慢变化的，可以近似为空间均匀流场。对于均匀流场，插值本身并不带来额外误差。本文后面的数值模拟结果表明，这种重叠网格处理方法是非常有效成功的。值得说明的是，若采用非结构化贴体网格，或者浸没边界法[23-26]、格子玻尔兹曼方法[27-29]等来处理椭球体绕流问题，在生成网格方面不会有困难，然而其数值模拟结果精度不如此处的O 型六面体贴体网格。

图1 倾斜置于流场中椭球体O 型网格划分示意图：(a)非重叠网格;(b)非重叠网格局部放大图;(c)重叠网格外层;(d)重叠网格内层Fig.1 O-type mesh sketch for a slanted spheroid: (a)non-overset mesh;(b)zoom-in for non-overset mesh;(c)outer part in overset mesh;(d)inner part in overset mesh

本文的网格离散采用开源的Gmsh 程序[30]。此程序采用脚本语言来生成三维几何模型，进行网格离散。因为本文算例数量较大，不同算例的几何模型以及网格离散都需要修改，采用脚本语言极大程度地减小了在建模与网格离散方面的工作量。

2 结果与讨论

2.1 阻力系数，圆球标准阻力曲线，以及阻力修正因子

物体的阻力定义为沿来流方向所受流体作用力，其常用无量纲阻力系数来表征

式中，Fd为物体受到的沿来流方向作用力，ρ为流体密度，A为物体迎风面积，Ur表示物体速度与假设没有物体存在时流体的当地速度之间的差值。在通过沉降法来测定阻力的实验中，Ur就是物体的最终沉降速度。根据不同的实验数据以及适用范围，前人给出了多种经验与半经验公式[4]。其中，在Re ＜105范围内，使用较为广泛的是Clift-Gauvin[31]公式

式(2)右边第一部分是Schiller-Nauman 公式[4]，在Re ＜800 条件下其误差估计为-4%～5%之间。本文的主要研究目标是椭球体。为了比较椭球体与等体积圆球在同等雷诺数条件下的阻力，引入阻力修正因子

即椭球阻力与圆球阻力的比值。此修正因子依赖于雷诺数，以及椭球的空间取向。

图2 给出了长径比Ar=0.25,0.5,1,2,4,8等6 种椭球体，当其回转轴与来流方向一致时(ϕ=0°)，在雷诺数Re=0.1,1,10,100,1000等条件下的阻力修正因子。修正因子中的圆球阻力采用经验公式（2）进行计算。对于Ar=1 的圆球而言，模拟得到的修正因子在Re=0.1,1,10,100 等雷诺数条件下都基本为1，相对误差分别为1.8%，2.9%，3.9%和0.7%，完全位于经验公式本身的误差范围内，这表明阻力的数值模拟非常精确。而在Re=1000 时，修正因子数值模拟结果为K=0.898，即相对误差为-10.2%。此误差较大，其产生根源将在2.3 节详细讨论。对于模拟的所有长径比的椭球体，当雷诺数从0.1 增长至1 时，阻力修正因子基本不发生变化，也就是说不论是圆盘或者细长体，在低雷诺数时其阻力对来流速度的依赖性与圆球是一样的，即随着雷诺数增大而线性上升。随着雷诺数的增大，形状偏离圆球越厉害的椭球体，其修正因子也更加偏离1。圆盘类椭球体其阻力大于同体积的圆球，而细长的椭球体阻力则小于圆球。这是因为在较高雷诺数条件下，压差阻力占主导地位（将在2.2 节进一步讨论），而圆盘类椭球体具有更大的迎风面积。

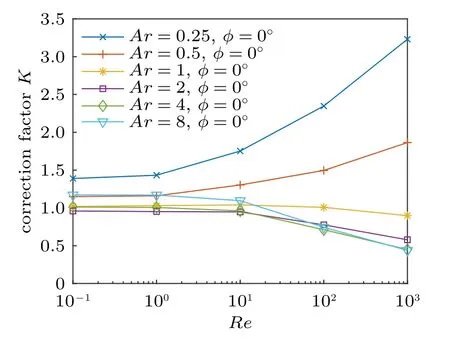
图2 不同雷诺数下椭球阻力修正因子Fig.2 Correction factor under various Reynolds number

图3 给出雷诺数Re分别为1,10,100,1000时不同攻角条件下的阻力修正因子。Re=0.1 条件下的结果与Re=1 基本相同而没有在图形中给出。在雷诺数较小时，修正因子对方向角ϕ的依赖性较小；随着雷诺数增大，这种依赖性也不断增大。特别地，在Re=1000 时，对于圆盘状椭球体(Ar=0.25,0.5)，在倾斜置于流场中时其修正因子急剧增大。在ϕ=15° 时,Ar=0.25 椭球体的修正因子达到了K=6.29，比其在ϕ=0° 时的修正因子K=3.23 还要大近乎一倍。这是非常特别的结果，因为ϕ=15° 时椭球的迎风面积要小于ϕ=0°，但其阻力（主要为压差阻力）却远远大于将椭球最大截面横置于流场中的情况。进一步的分析表明，这是由于两种条件下的流动形态非常不同（细节将在2.3 节给出）。除去圆盘状椭球体在高雷诺数时表现出的特别形态，其他条件下的修正因子都表现出了类似的一般性，即修正因子的极值出现在两种特定的方向角上：对于圆盘状椭球，当ϕ=0°时其修正因子最大，而当ϕ=90° 时其修正因子最小；对于细长型椭球，情况则刚好相反。这种现象可以从阻力的两部分构成中得到解释（将在2.2 节进一步讨论）。

图3 不同来流攻角下椭球阻力修正因子：(a)Re=1；(b)Re=10；(c)Re=100；(d)Re=1000Fig.3 Correction factor with respect to ϕ : (a)Re=1;(b)Re=10;(c)Re=100;(d)Re=1000

在Re →0 的理想条件下，椭球稳定绕流问题可以解析求解。对于ϕ=0°与ϕ=90° 两种取向的椭球，其所受阻力可通过较为简单的解析式来表达[4]。而对于任意倾角的椭球，则可以通过ϕ=0°与ϕ=90° 两种倾角下结果的线性叠加得到，即

式中，Fd‖与Fd⊥分别表示椭球回转轴平行与垂直于来流时所受的阻力。为了检验上面的线性叠加方法在雷诺数不等于零时的有效性，在图3 中也给出了根据式（4）计算得到的任意倾角的修正因子（图中的虚线）。从图中可以看出，除圆盘状椭球体在Re=1000 时的结果，其他条件下，这种基于线性叠加原理的处理方式，仍然可以给出较好的结果。

2.2 形状阻力与黏性阻力

为了进一步了解阻力的变化规律，这里详细讨论阻力的组成部分，即形状阻力与黏性阻力。物体在垂直来流方向的迎风面积对形状阻力有着决定性的作用。黏性阻力主要决定于物体平行于来流方向的表面受到的黏性剪切力，而剪切率可近似认为正比于来流速度，所以黏性阻力大体上与来流速度呈正比关系。这种正比关系在Stokes流动条件下是精确满足的。而本文的数值模拟结果表明，对于所有形状的椭球颗粒，在任意来流攻角条件下，在整个模拟的雷诺数范围内（0.1～1000），黏性阻力基本上随着雷诺数增大而线性上升。

图4 给出了数值模拟得到的形状阻力Cdp与黏性阻力Cdf的比值。图4(a)是在Re=0.1 时不同来流攻角条件下的结果。当椭球回转轴与流向一致时 (ϕ=0°)，在Re →0 时Cdp/Cdf存在理论解[4]，即图4(a)中左侧黑色圆圈所标示的结果。模拟结果与此理论解吻合得很好。对于细长的椭球，此比值接近于零，即形状阻力占比很小，总阻力基本由黏性阻力构成。对于圆球(Ar=1)，此比值为熟知的1∶2。而对于扁平的椭球，形状阻力占比则随着长径比的减小而急剧上升。当椭球改变其空间取向时，Cdp/Cdf随来流攻角单调变化；扁平椭球随攻角增大而减小；细长椭球随攻角增大而增大。特别地，在攻角约为55° 时，不同长径比的椭球体此比值都接近，约为1∶2。图4(b)是不同雷诺数下形状阻力与黏性阻力之比。图中给出了本文模拟中最极端的两个长径比Ar为0.25和8 以及圆球的结果。从图中可以看出，在雷诺数小于10 的条件下，Cdp/Cdf基本不随雷诺数变化。之后，随着雷诺数的增大，此比值不断增大，即形状阻力占比不断上升。而对于扁平的椭球体，形状阻力随雷诺数增大上升更加显著。

图4 形状阻力与黏性阻力比值：(a)Re=0.1 数值模拟结果(ϕ=0 时黑色圆圈对应于 Re →0 时的理论解);(b)不同雷诺数下数值模拟结果Fig.4 Ratio between form and friction drags: (a)results for Re=0.1 (Black circles at ϕ=0 corresponding to theoretical results when Re →0 ;(b)results under various Reynolds number

2.3 流动形态

圆球绕流随着雷诺数的上升展现出不同的形态[4]：在雷诺数接近零时，绕流前后对称；随着雷诺数上升，绕流前后慢慢变得不对称，大约在Re=20 时，后缘出现流动分离，直到大约Re=130，存在稳定的尾流区；而随着雷诺数进一步增大，直到大约Re=400，尾流开始失稳；再进一步增大雷诺数，尾流失去轴对称性，产生非定常的脱落涡。

本文的数值模拟结果表明，对于回转轴与流向一致时的椭球绕流，其流动形态发展过程与上述球体类似。然而，发生不同形态转变时的雷诺数则极为不同。在2.1 节讨论不同雷诺数下各种形状椭球阻力时，发现Ar=0.25 的扁平椭球在Re=1000时表现出完全不同的特性。这里特别分析此形状椭球在不同来流攻角条件下的流动形态，进而揭示其特殊阻力表现的根源。

图5 给出了ϕ为 0°,15°,60°时3 种来流攻角下的速度以及压力在x-y中截面云图。在速度云图中，同时给出了流线图。因为流动的三维不稳定性，流线并不一定位于x-y截面内，因而在平面图形中会出现流线相交的假象。在ϕ=0°时（图5(a)，图5(b)），速度与压力云图都呈现出上下对称性，在尾流处有一对稳定的涡，形成较强的负压中心。在对图5(a)中的流线进行仔细分析时发现，这一对涡分别向x-y截面的两侧偏离，表明尾流沿着椭球回转轴方向具有一定的螺旋性。这一现象在圆球尾流中也早被发现[4]。而当椭球稍稍倾斜至ϕ=15° 时，尾流则发生极大改变，速度与压力场都不再上下对称，而尾流区的流线也非常杂乱。此时，尾流区不再有快速旋转，伴随较低负压的涡旋，而椭球后缘整体的压力相对ϕ=0°时有明显下降，这也意味着更大的压差阻力。这种尾流结构的差异正是2.1 节（图3(d)）所讨论阻力异常变化的根源。而当椭球长边近似顺流向放置时（图5(e)，图5(f)），流动分离的尾流区急剧减小，流体基本顺着椭球表面流过，前缘的高压区大大减小，而后缀也不存在强的负压区，从而使得压差阻力大大减小。此处讨论的现象类似于经典的翼型绕流在较大攻角下发生的失速现象。

图5 Re=1000 时 Ar=0.25 椭球体绕流速度及压力云图：(a)ϕ=0° 速度云图（包括流线）；(b)ϕ=0° 压力云图；(c)ϕ=15° 速度云图（包括流线）；(d)ϕ=15° 压力云图；(e)ϕ=60° 速度云图（包括流线）；(f)ϕ=60° 压力云图Fig.5 Velocity and pressure contours for ellipsoid with Ar=0.25 at Re=1000 : (a)velocity contour (with streamlines)for ϕ=0° ;(b)pressure contour for ϕ=0° ;(c)velocity contour (with streamlines)for ϕ=15° ;(d)pressure contour for ϕ=15° ;(e)velocity contour (with streamlines)for ϕ=60° ;(f)pressure contour forϕ=60°

2.4 非球阻力经验公式对比分析

最早的非球阻力经验公式[8]只用一个参数圆球性(sphericity)来表示任意的非球颗粒，其定义为ϕ=Ssphere/S，即等体积球体的面积Ssphere与其实际面积S之比。此公式非常简便易用，但其不足也十分明显，因为ϕ并不能表征颗粒的实际空间取向，而且ϕ也无法区别形状性差异非常大的颗粒，比如扁平与细长的颗粒，ϕ可以完全相同，都是比1 小的数值。

对于Stokes 阻力，圆球形状阻力与黏性阻力之比为1∶2。基于此结论，Leith[9]提出任意颗粒的阻力也可分为1∶2 的两部分，其中，黏性阻力采用体积等效球体来计算，而形状阻力则采用垂直迎风面积等效球体来计算。

圆球阻力与来流速度的关系，从线性的Stokes 阻力区慢慢过渡到平方关系的牛顿阻力区。Ganser[10]认为这种关系对任意形状颗粒都成立，从而提出一种新的阻力经验公式框架，连接Stokes 阻力与牛顿阻力。在此框架中，需要给出任意颗粒的Stokes 阻力与牛顿阻力。而对于Stokes 阻力，Ganser[10]借鉴了前面所述的Leith[9]方法，并进行了修正。

Tran-Cong 等[12]采用两个参数，即等投影面积圆球直径与等体积圆球直径之比，以及颗粒的圆周性（circularity），即在垂直流动方向截面上等投影面积的圆周长度与其实际周长之比，来表征非球颗粒。通过拟合其实验数据，给出了新的经验公式。

Holzer 等[18]部分采用Ganser[10]与Tran-Cong等[12]的结果，并引入沿流向圆球性参数，来替代Leith[9]经验公式中的横向圆球性参数，给出了自己的经验公式。

Loth[13]回顾分析了多种阻力经验公式及实验数据，认为Ganser[10]提出通过连接Stokes 阻力与牛顿阻力而给出其间过渡区阻力的方法是行之有效的。但其提出针对不同类型的非球颗粒，应该采用不同的几何形状参数：对于回转椭球体，长径比是最佳的；对于规则颗粒，圆球性参数是最佳的；而对于不规则颗粒，最佳的则是大-中-小面积比（max-med-min area ratio,即由颗粒最大、中间以及最小尺寸定义的参数，类似于Corey 形状函数）。

本文将数值模拟结果与上述流行的非球颗粒经验公式进行了对比。表1 给了这些经验公式的出处，而图6 与图7 则分别给出了不同攻角下，Ar为0.25 与8 的两种椭球颗粒分别在Stokes 阻力区与牛顿阻力区的阻力系数。Ar=0.25 是本文数值模拟中最扁平的椭球体，而Ar=8 则是最细长的，其他长径比的结果位于这两者之间，没有详细给出。而在Stokes 阻力区与牛顿阻力区之间雷诺数条件下的结果，则如Ganser[10]发现的那样，其在两者之间单调过渡，此处也没有详细给出。通过对比在Stokes 与牛顿阻力区的数值模拟结果以及各种经验公式，基本可以反映出数值模拟与经验公式对非球颗粒阻力预测能力的精度。

表1 非球颗粒经验阻力公式Table 1 Empirical drag formulas for non-spherical particle

图6 不同攻角下椭球体Stokes 阻力(Re=0.1)数值模拟与经验公式对比,所有结果都以 Re →0 时的理论解的最大值（在 ϕ=0° 时取得）进行无量纲化：(a)Ar=0.25 ;(b)Ar=8Fig.6 Drag coefficient comparison from simulation and empirical formulas under Re=0.1,normalized by the maximum drag under Re →0 at ϕ=0° : (a)Ar=0.25 ;(b)Ar=8

图7 不同攻角下椭球体Newton 阻力(Re=1000)数值模拟与经验公式对比,所有结果都以 Re=1000 时的圆球阻力进行无量纲化：(a)Ar=0.25 ;(b)Ar=8Fig.7 Drag coefficient comparison from simulation and empirical formulas under Re=1000,normalized by the drag of volumeequivalent sphere: (a)Ar=0.25 ;(b)Ar=8

对于Re →0 的Stokes 流动，Oberbeck 最早求解了任意长径比的椭球在其对称轴平行或垂直流动方向的流动问题[4]。而对于任意的来流攻角，则可以使用平行与垂直方向的结果线性叠加得到。对于Ar ＜1 的椭球，当其回转轴沿流向时其阻力最大；而对于Ar ＞1，则是回转轴垂直流向时阻力最大。不论何种长径比，都是迎风面积最大时，阻力最大。图6 中显示的在Re=0.1 时的数值模拟结果与理论解趋势完全一致，但稍稍大于理论解。这种偏大是由于非零的雷诺数条件下存在的对流项形成的[4]。在所有的经验公式中，Loth[13]给出的结果与理论解以及本文的数值模拟最为接近。这其实是因为此处采用的Loth 公式本身就应用到了理论解。Haider 等[8]与Ganser 的经验模型都没有考虑颗粒的取向，所以在图6 中都是水平直线。特别地，Holzer 公式给出了相反的趋势。综合而言，除了实质上考虑理论解的Loth 公式，其他公式给出的结果都不太好。而当Ar趋近于1（即接近圆球）时，这些经验公式的误差都减小，因为所有的经验公式都实质上采用了圆球的理论解。

而在Re=1000 时，圆球开始进入牛顿阻力区，即其阻力系数之后基本不随雷诺数变化（当Re ＜3×105）。扁平的椭球横置于流场中时，其更早进入牛顿阻力区。而细长的椭球体，则还没有进入牛顿阻力区。图7 中的椭球阻力，都以对应的圆球阻力为标准进行了无量纲化。只有当椭球迎风面积相对较小时，其阻力系数小于圆球；对于扁平的椭球横置于流场中时，其阻力远大于圆球。若以数值模拟结果作为参照标准，Holzer公式给出的结果最好。在数值模拟中观察到的Ar=0.25 的扁平椭球在ϕ=0～15° 时阻力突然增大（上面章节已经阐释了其物理机理），这在所有的经验公式中都没有体现。相对来说，Haider公式对于细长的椭球体给出的阻力远远大于其他经验公式以及数值模拟结果，这应该是不正确的，其根源是因为公式中采用的唯一参数圆球性(sphericity)对于细长的椭球不太适合，此时椭球表面积相对同体积的圆球而言非常大，使得圆球性参数远离1，从而相对圆球而言，给出了“过度”的阻力修正。

综合考虑本文数值模拟与各种经验公式，可以看出对非球颗粒的阻力精确预估是非常困难的问题。尽管已经有较大量的实验数据，提出了多种不同的拟合方法，但没有一种方法能给出最佳结果。而针对具体颗粒形状的数值模拟，可以认为是精度最高的结果。通过累积更多的高精度数值模拟结果，有望给出更完善的经验公式。

3 结论

颗粒在无界均匀流场中的阻力是颗粒多相流领域最基本的问题之一。对于球形颗粒，其阻力与雷诺数间的关系曲线被称为标准阻力。而在相关的工程应用与科学研究中，颗粒基本都是非球形。对于非球颗粒的阻力，最简略的估计是采用相同体积的圆球阻力来近似。为了提供更精确的阻力估计，不同学者尝试引入多种不同的几何形状参数，结合实验数据，给出不同的阻力系数经验公式。本文通过高精度数值方法，较系统模拟研究了从扁平到细长的一系列椭球体，在常见颗粒雷诺数范围（0.1～1000）内，不同来流攻角条件下的阻力。数值模拟结果发现，对于本文所考虑的长径比0.25～8 之间的所有椭球，在雷诺数从0.1 增大到1000 的过程中，其黏性阻力均随着雷诺数而线性增大。而其形状阻力在Stokes 流动条件下也随着雷诺数线性增大，但随着雷诺数的增大，形状阻力逐渐过渡到与雷诺数平方成正比，即进入牛顿阻力区。对于扁平的椭球，当其以更高迎风面积横置于流场中时，其在更小雷诺数条件下就进入牛顿阻力区。而对于细长的椭球，其则在更大雷诺数条件下进入牛顿阻力区。在Stokes 与牛顿阻力区之间，颗粒阻力基本上单调变化。对于颗粒在过渡区的阻力，通过确定其Stokes 与牛顿阻力之后，采用特别定义的无量纲参数插值来确定[10]——这一方法在理论及实践上都表现出其合理性。

以Stokes 流动条件椭球绕流的理论解作为标准，对比本文的数值模拟方法与各种经验公式，发现数值模拟给出了最佳精度。在更一般的雷诺数范围内，数值模拟结果与各种经验公式大体相符。但模拟结果与各种经验公式结果展现出了较大的散布性，而这种散布性，随着雷诺数的增大而增大。各种适用的经验公式及本文中的大部分算例都表明，在给定来流速度条件下，椭球的阻力随着迎风面积增大而增大。然而，在Re=1000时，对于扁平的椭球，数值模拟给出了不一样的结果：当椭球回转轴与流向一致时，其受力比倾斜放置要小很多，尽管前一情形下迎风面积更大。对流动结构的进一步分析表明，这是因为轴对称条件下，尾流区域更稳定，减小了压差阻力损失。综合各种因素，有理由相信在对给定形状颗粒的阻力确定方面，本文的数值模拟方法比各种针对更一般形状颗粒的经验公式更加精确。累积更大量的高精度数值模拟结果，有望给出具有更高精度、更有适应性的阻力公式。