社会消费品零售总额模型预测实证研究

徐延军

（河南君友数字科技有限公司，河南 郑州 450008）

一、引言

2023年以来，各地政府将恢复和扩大消费作为优先任务，相继出台了一系列促进消费的政策。然而，目前经济恢复仍然面临需求不足、结构性矛盾与周期性问题相互交织以及消费市场恢复基础不够巩固等挑战。为了推动消费增长回归正轨，充分利用和发挥促消费政策作用，提高政府决策的科学性、针对性和精准性，及时进行消费运行预测显得尤为重要和紧迫。社会消费品零售总额（以下简称“社消零总额”）是反映国内消费市场状况的重要指标，准确预测社消零总额对了解消费市场趋势、加强政府市场调控、促进经济增长具有重要的实际意义。

目前，国内学者已经采用多种方法对社消零总额进行预测。罗艺和肖李春（2022）使用多元线性回归方法分析了地方财政支出、居民消费价格指数、年末常住人口数和居民人均可支配收入等因素对社消零总额的影响。蒋翠清和乔晗（2022）则结合股市数据建立了累计增幅预测模型，发现长短期记忆神经网络在预测效果上表现最好。李方一和肖夕林等（2016）将百度搜索指数与传统经济指标结合，建立多元回归模型验证了网络搜索数据与社消零总额之间的相关性。总体而言，国内学者在选择指标和构建模型时虽考虑了社消零总额的影响因素，但存在以下局限：一是缺乏将政府统计数据和网络大数据结合的研究；二是指标的时效性较差，多为历史数据验证分析，实际应用的可操作性有限；三是缺乏对比分析和统一的评价标准，无法科学系统地评估最优模型。

本文借助大数据技术获取与社消零总额高度相关的同趋势观测变量，并基于这些变量构建深度机器学习模型。同时，与传统计量经济学模型进行对比分析，以直观展现机器学习模型在经济运行预测应用方面的优越性。通过这种方式，可以更准确地预测社消零总额，提升预测精度，更好地应对经济运行中的不确定性和复杂性。

二、研究思路

本文以大数据技术为基础，结合计量经济学模型和机器学习算法，旨在探索实现消费运行可预测性变革。具体而言，选取2018年1月至2022年12月的河南省月度社消零总额数据，分别构建ARIMA、SARIMA、SARIMAX模型。

研究分为以下几步：

（1）数据准备。多渠道获取河南省月度社消零总额数据，通过相关性分析筛选若干影响社消零总额的观测指标。采用差分法，对非平稳月度社消零总额数据进行平稳操作。

（2）构建模型。确定训练集和测试集，调试模型参数，分别构建ARIMA、SARIMA、SARIMAX预测模型。

（3）评估模型。采用MSE（均方误差）、RMSE（均方根误差）、MAE（平均绝对值误差）和MAPE（平均绝对百分比误差）指标对三种模型预测结果进行评估，选取最优模型。

（4）实施预测。选取最优模型，预测2023年1—11月河南省月度社消零总额。

三、数据准备

（一）数据来源

按照全面性、可靠性、可获取性和时效性原则，选取解释变量。解释变量分为历史数据和观测数据。其中，历史数据来自商务部门重点企业监测数据、统计部门年度统计公报及《统计年鉴》等。观测数据来自现有数据合成、百度搜索引擎、专项统计调查、平台实时监测、网站定期发布。具体如下：

现有数据合成。提取不同平台反映网络零售发展情况的一系列指标，形成时间序列数据，构建网络零售发展指标体系，进行指数合成。

百度搜索引擎。百度提供关键词搜索指数，反映与该关键词相对应的某类商品的热门程度和被关注度。

平台实时监测。运用大数据抓取技术，实时监测淘宝、天猫、京东、拼多多、抖音、当当、唯品会、国美、苏宁等平台商品零售额、城乡商品交易量占比数据。

网站定期发布。乘联会每周公布当周乘用车日均销量；国家发展和改革委每月发布油价调整通知；国家统计局发布采购经理人指数、消费者信心指数；邮政管理局发布当月快递件数。

（二）指标体系

结合已有研究和统计实践，通过分析社消零总额构成，引入与社消零总额具有高度相关性的同趋势观测指标，见表1。运用相关性分析，确定社消零总额预测的历史数据与观测数据。

表1 社消零总额预测指标体系

四、预测模型

国内学者多基于ARIMA模型预测社消零总额，未考虑预测模型的季节性因素，也未引入同趋势观测变量参与预测，短期内模型预测误差相对较小，随着时间跨度增加预测误差逐步增大。时间序列数据是长期趋势、季节变动、循环波动、不规则波动等变化形式的叠加或耦合，结合时间序列数据特点，本文分别构建ARIMA、SARIMA、SARIMAX模型进行社消零总额预测，并对比三种模型拟合情况，选取最优模型进行预测分析。

（一）ARIMA模型

ARIMA模型（Auto-Regressive Integrated Moving Average Model）也被称为“自回归移动平均模型”，即ARIMA（p，d，q）模型。其中，p、d、q分别代表模型中自回归阶数、差分阶数、移动平均阶数。该模型先将非平稳时间序列转化为平稳时间序列，然后对因变量的滞后值以及随机误差项的现值和滞后值进行回归预测。模型考虑数据时间特性和相关性，能够捕捉到数据趋势变化，为决策者提供准确预测和相应决策依据。模型表示为：

其中，Yt为t时刻的预测量，B为后移算子，et、c分别为残差序列、常数项。

（二）SARIMA模型

SARIMA模型（Seasonal Auto-Regressive Integrated Moving AverageModel）也被称为“季节性差分自回归滑动平均模型”，即在ARIMA模型基础上引入季节性因素，转化为SARIMA（p，d，q）（P，D，Q）s模型。SARIMA共有7个参数，其中，p为非季节自回归最大滞后阶数，d为非季节差分次数，q为非季节移动平均算子的最大滞后阶数，P为季节自回归算子的最大滞后阶数，D为季节性差分次数，Q为季节移动平均算子的最大滞后阶数，s为季节长度或周期大小。SARIMA模型通过考虑社消零总额的季节性特征，能够更准确地捕捉到季节性变动对社消零总额的影响。模型表示为：

其中，Φp（B）=1-Φ1B-Φ2B2-…-ΦpBp为相邻时刻之间的p阶自回归算子，p为自回归阶数；θq（B）=1+θ1B+θ2B2+…+θqBq为相邻时刻之间q阶自回归算子，q为移动平均阶数；ΦP（BS）=1-Φ1B-Φ2B2-…-ΦPBP为相邻时刻之间P阶自回归算子，P为季节性自回归阶数；θQ（BS）=1+θ1B+θ2B2+…+θQBQ为相邻时刻之间的Q阶自回归算子，Q为季节性移动平均阶数。

（三）SARIMAX模型

SARIMAX模型（Seasonal Auto-Regressive Integrated Moving Averagewith eXogenous factors Model），也被称为“季节性自回归综合移动平均外生模型”，即SARIMAX（p，d，q）（P，D，Q）s（X）模型，在ARIMA模型基础上考虑季节性因素（S，Seasonal），引入外生观测变量（X，eXogenous）辅助预测。SARIMAX模型通过结合季节性因素和外生观测变量，能够更好地捕捉和解释时间序列数据中的复杂性和潜在规律，进而提高模型预测能力。实际应用中，SARIMAX模型常用于对经济指标和市场趋势进行预测。模型表示为：

其中，Xi，t-k为t-k时刻的第i外部因素，i为外部因素个数，k为第i个影响预测变量的外部因素的回归阶数，αik为第i个外部因素k时刻的回归系数，其他参数同式（1）和式（2）。

（四）评价指标

评价模型预测效果的常用指标包括MSE（均方误差）、RMSE（均方根误差）、MAE（平均绝对误差）和MAPE（平均绝对百分比误差）。核心思想为度量预测值与真实值之间的差异程度，指标数值越小，预测模型效果越好。反之，则预测误差较大。上述评价指标仅为度量预测误差，不能单独作为判断模型好坏的唯一依据。计算公式为：

其中，yi是第i个测试样本的实际值，是第i个测试样本的预测值，n代表测试样本数量。本文选取上述四个指标比较不同模型的预测准确性，综合分析各模型的预测效果。

五、实证分析

运用SPSS软件构建ARIMA模型与SARIMA模型，基于Python语言建立SARIMAX模型，选取2018年1月至2021年12月数据作为训练集，2022年1月至2022年12月数据作为测试集进行测试，分别预测河南省月度社消零总额。其中，ARIMA模型仅考虑社消零总额时间序列特征；SARIMA模型引入影响社消零总额的季节性功能；SARIMAX模型引入影响社消零总额的季节性功能以及同趋势观测变量。

（一）ARIMA模型预测

先对河南省月度社消零总额数据进行平稳性检验，通过1阶差分运算，转化为平稳时间序列。然后对平稳时间序列分别计算自相关系数ACF和偏自相关系数PACF，得到最佳阶层和阶数，确定模型d、p、q的取值范围。最终确定ARIMA（3，1，13）为最优预测模型，平稳R方值为0.671，BIC①AIC（赤池信息量）、BIC（贝叶斯信息量）为在训练模型中选择更好模型时的判断准则。AIC、BIC越小，模型越好，通常选择AIC或BIC最小的模型。值为12.248。预测结果如表2所示，ARIMA模型存在预测准确性不稳定的问题，表现为2月社消零总额误差率达到28.6%，12月社消零总额误差率仅为0.3%，极差超过20%，有较大的改善空间。

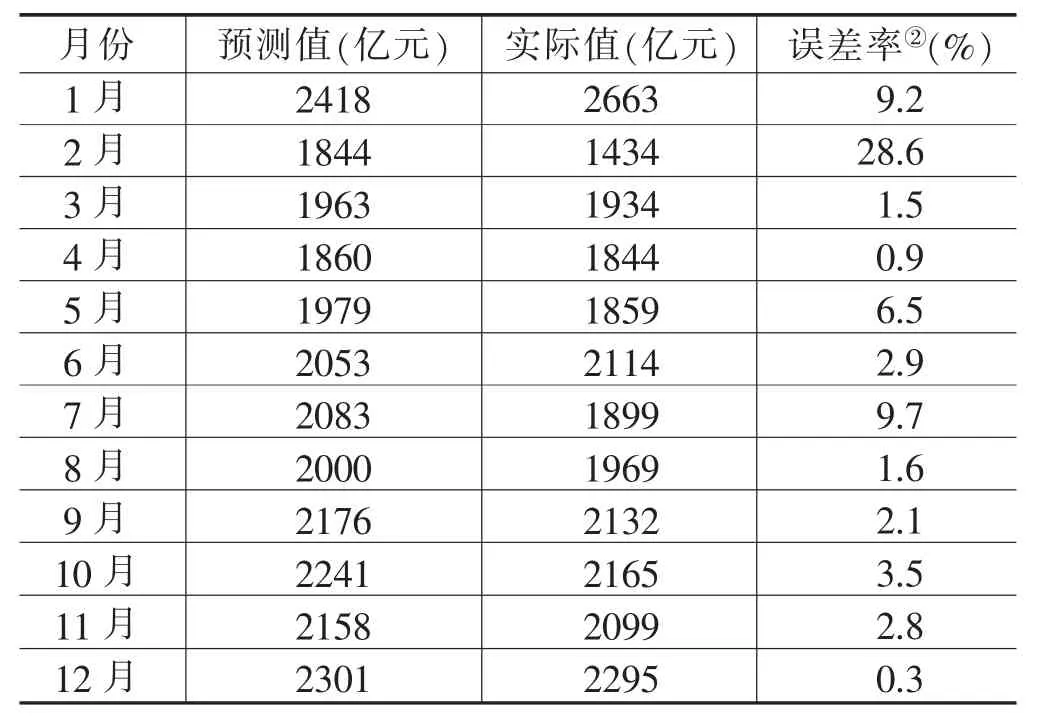
表2 基于ARIMA模型的2022年1—12月社消零总额实际值与预测值

（二）SAR IMA模型预测

结合社消零总额数据特点，确定SARIMA模型季节性周期值S为12。先对河南省月度社消零总额数据进行平稳性判断分析，将其转化为平稳时间序列。然后分别确定季节性与非季节性差分阶数，即D和d。再运用PCA和FPCA定阶，确定季节性与非季节性阶数，即p、q和P、Q。通过对模型参数进行残差检验，确定拟合度最优模型SARIMA（1，1，6）（1，0，1）12，平稳R方值为0.804，BIC值为11.157。预测结果如表3所示，SARIMA模型整体预测相对稳定，但1月、2月、4月、6月、10月和11月这6个月误差率均超过5.0%，模型预测精度有待提升，仍有一定的改善空间。

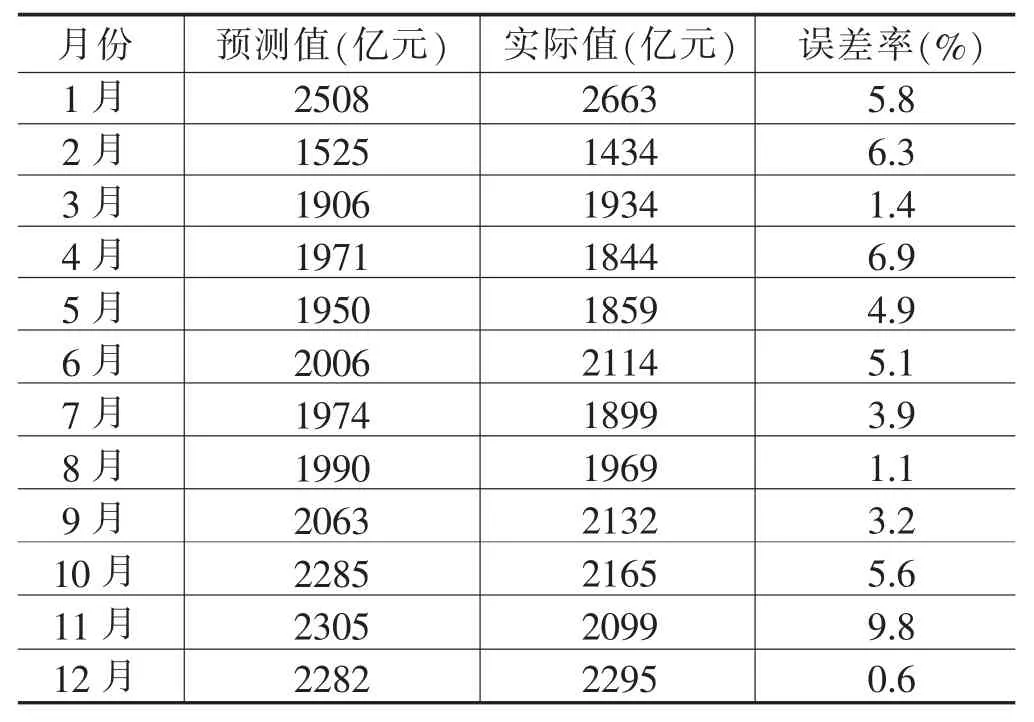
表3 基于SARIMA模型的2022年1—12月社消零总额实际值与预测值

（三）SARIMAX模型预测

先对数据进行预处理，选取预测模型观测变量，使用网格搜索进行超参数调优，拟合出729种模型，按照AIC准则进行甄选，最终选定最优模型SARIMAX（1，1，0）（0，2，2，12），AIC的值为2.111。预测结果见表4，SARIMAX模型具有较强预测能力，预测准确性比较稳定，除2月和8月误差率超过5.0%外，其他月份误差率则稳定在3.0%左右，能够实现对社消零总额的有效预测。

表4 基于SARIMAX模型的2022年1—12月社消零总额实际值与预测值

（四）模型预测效果对比分析

图1显示出三种模型测试集的拟合效果。可以看出，三种模型预测值与社消零总额实际值走势大致趋同，但SARIMAX模型的预测效果更贴近实际值，可以有效预测实际变动趋势。相比之下，ARIMA模型和SARIMA模型的预测效果不太稳定，在个别月份出现较大的误差波动。具体看，在2022年5月和8月，社消零总额均呈现小幅上升态势，而ARIMA模型的预测结果却是大幅上升和小幅下降。在2022年10月和11月，社消零总额呈现小幅上升和小幅下降态势，而SARIMA模型的预测结果却是大幅上升和小幅微升。需要注意的是，由于统计局未公布2022年1月和2月单月社消零总额，本文根据统计经验，将1—2月社消零总额累计数据换算成月度数据，造成三种模型1月和2月预测值与实际值走势偏差较大，误差率普遍较高。整体看，SARIMAX模型在预测中表现相对较好，其拟合效果整体优于其他两种模型。

图1 三种模型预测值对比

为进一步分析比较ARIMA、SARIMA和SARIMAX模型，引入模型评价指标，计算结果如表5所示。具体看，ARIMA模型预测中出现较高误差，MSE为24446，RMSE为156.4，MAE为106.8，MAPE为5.8，表明ARIMA模型预测结果与实际值之间存在较大差距，预测误差率较高，需进一步调整模型参数或改进模型结构以提高预测准确性。SARIMA模型相对ARIMA模型显示出更好的性能，具有较低的MSE（11430）、RMSE（106.9）、MAE（92.0）和MAPE（4.6）值，该预测结果与实际值间误差相对较小。SARIMAX模型MSE（4304）、RMSE（65.6）、MAE（54.8）和MAPE（2.8），预测误差进一步减小，是三种模型中的最佳模型，在各评估指标中均显示出最优性能，预测优势明显。

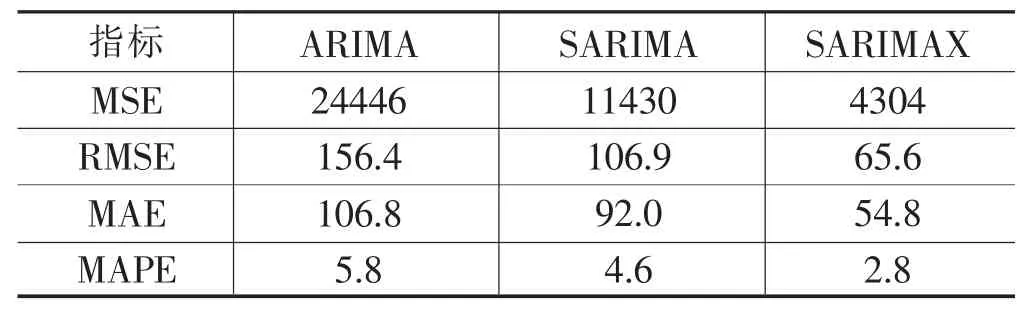
表5 ARIMA、SARIMA、SARIMAX模型评估指标对比

综上所述，三种模型预测准确性从高到低依次为SARIMAX模型、SARIMA模型、ARIMA模型。多变量SARIMAX模型在精准性和稳定性上优于单变量的ARIMA和SARIMA模型，而SARIMA模型因考虑季节性因素，预测效果优于ARIMA模型。机器学习算法相对于传统的统计预测方法，具有一定优越性，与已有研究相吻合。

（五）基于SARIMAX模型社消零预测分析

结合模型预测结果对比分析，选取SARIMAX模型预测2023年1—11月河南省社消零总额，预测结果见表6。

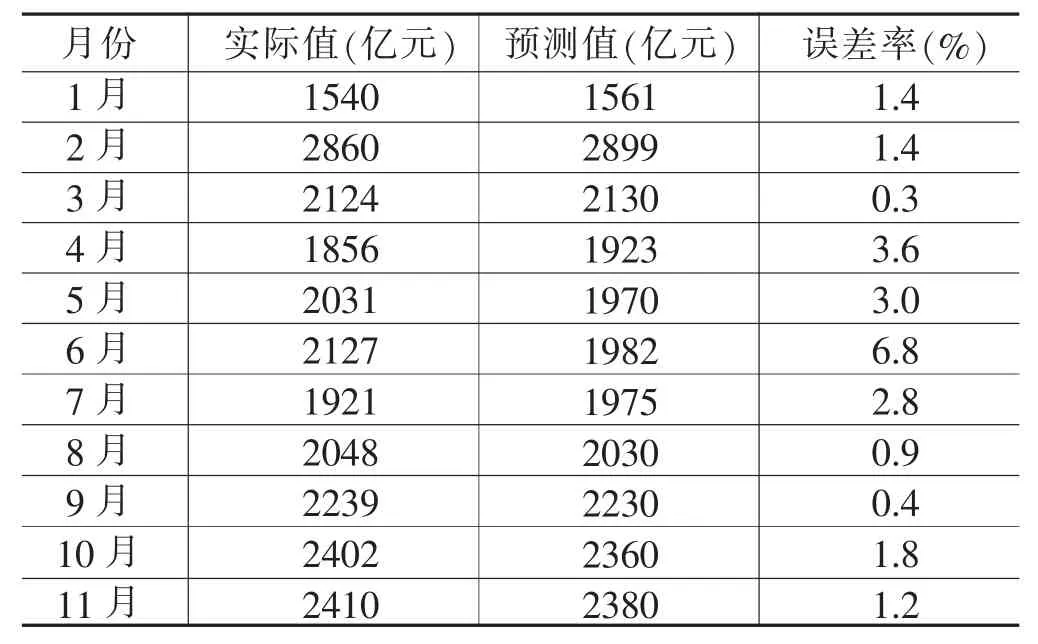
表6 2023年1—11月河南省社消零总额实际值与预测值比较

从2023年1—11月预测结果看，6月河南省社消零总额预测误差率达6.8%，预测值与实际值出现明显误差，可能与统计数据季节性调整相关；3月、8月和9月社消零总额预测效果最为理想，误差率不足1.0%；其他月份预测误差率均控制在3.0%左右。整体而言，SARIMAX模型能够较为精准反映社消零总额月度走势情况，模型预测具有较高精准度与较好时效性，能够更好地为河南省消费品市场进行宏观调控和分类指导服务，高效统筹布局河南省经济发展，实现宏观经济运行逆周期调节。

六、总结与展望

本文利用2018—2022年河南省的月度社消零总额数据，分别构建了ARIMA、SARIMA和SARIMAX模型，并利用这些模型对2022年河南省月度社消零总额进行预测。通过引入预测模型评价指标进行评估，确定SARIMAX模型为最优模型。随后利用该模型对2023年1—11月的河南省月度社消零总额进行了预测，预测结果误差率在0.3%—6.8%之间，预测效果较好。

根据研究结果，得出以下结论：首先，网络零售指标和快递规模指标与月度社消零总额之间存在较强相关性，为SARIMAX模型中的主要观测变量。其次，引入季节性因素的SARIMA模型在预测效果上明显优于ARIMA模型，预测精度提高了20.7%，改善效果明显。再次，引入外部变量的SARIMAX模型在预测效果上明显优于SARIMA模型，预测精度提高了39.1%，提升效果最为显著。最后，机器学习模型在模型参数确定和预测精度方面具有明显优势，预测效果优于传统的统计分析模型。

本文在研究方法和模型设计方面还存在一些不足之处，需要进一步深入和完善。首先，本文仅利用机器学习模型SARIMAX与传统统计分析模型ARIMA、SARIMA进行了对比分析，未来研究可以引入更多的机器学习模型，如支持向量机、随机森林、LSTM等来进行对比分析，以进一步验证SARIMAX模型预测的科学性和准确性。其次，受限于现实条件，本文引入的SARIMAX模型观测变量较少，不能涵盖影响社消零总额的所有影响因素。未来研究可以结合消费的新业态和新模式，引入更多高频指标，如线下消费活跃度、企业活跃度等，以提升对消费行为的预测和分析能力。

对社消零总额预测，具有以下意义：一是精准施策，靠前发力。先行掌握全省消费数据，有效解决数据滞后或无数据的现实痛点、难点，辅助政府及时掌握经济运行情况，为出台政策措施提供数据支撑和决策依据。二是针对重点领域、重要节点、重点企业，建立预警机制，对异常波动进行情况核实、原因分析、影响评估，从政策支持、融资协调等方面扶持引导，助力企业纾困解难。三是互联互通，数据共享。建立跨部门跨区域协同联动机制，将社消零数据与保供数据统一分析处理，打造多源融合数据底层架构，使消费分析更为精准，流通保供更加高效。