金刚石压机冷却水温控系统的设计

黄祥辉，朱晓东，任天平，苏宇锋

(1.郑州大学机械与动力工程学院，河南郑州 450001；2.郑州大学电气与信息工程学院，河南郑州 450001)

0 前言

六面顶压机是一种生产人造金刚石和立方氮化硼等超硬材料的生产设备，在高温高压环境下，通过触媒的催化作用，将石墨和六方氮化硼合成金刚石与立方氮化硼。研究表明：冷却循环水的温度对六面顶压机的顶锤寿命以及合成超硬材料质量的影响不可忽视[1-2]，要求水温在一定的区间内变化，因此需要控制系统智能调节，通过控制冷却水的温度来延缓锤头发生塑性变形的时间，有利于超硬材料的生产。

在实际生产过程中，通常采用常规PID控制，但常规PID控制更依赖于人工经验，且生产环境工况的复杂性以及温度控制的滞后性使得常规PID无法满足控制精度的要求，难以达到理想的效果[3]。文献[4]使用模糊PID来实现温度控制，但模糊规则依赖于人工经验，参数修正过于复杂，且受干扰的影响大。文献[5-6]使用BP神经网络来优化PID参数，具有一定的自学习能力，但存在训练收敛速度缓慢、收敛精度不足等问题。

鲸鱼算法(Whale Optimization Algorithm，WOA)是一种智能仿生优化算法，模拟座头鲸群寻找、包围、驱赶、捕食猎物的过程以实现对目标问题的优化求解。鲸鱼算法于2016年由澳大利亚学者 MIRJALILI和LEWIS提出[7]，具有操作原理简单、调整参数少、工程上易于实现、收敛速度快的特点，但标准鲸鱼算法存在局部最优的情况[8]。

基于此，本文作者以六面顶压机冷却水温控系统为研究对象，提出一种改进鲸鱼算法优化的BP-PID控制器，将改进后的WOA算法与BP神经网络相结合，实现快速收敛，避免局部最优；同时完成PID参数的自适应调整，并设计相应的硬件电路，提高温控系统的响应速度与控制精度，实现对冷却水温度的精确控制。

1 冷却水温控系统架构

1.1 系统流程

冷却水温控系统具有六路冷却管道，冷却水通过管道流经6个冷却锤头，温控系统调节流量阀，将锤头温度控制在适宜的范围内。系统热量主要通过冷却水作为热传导介质进行传递。冷却水系统水路原理如图1所示。

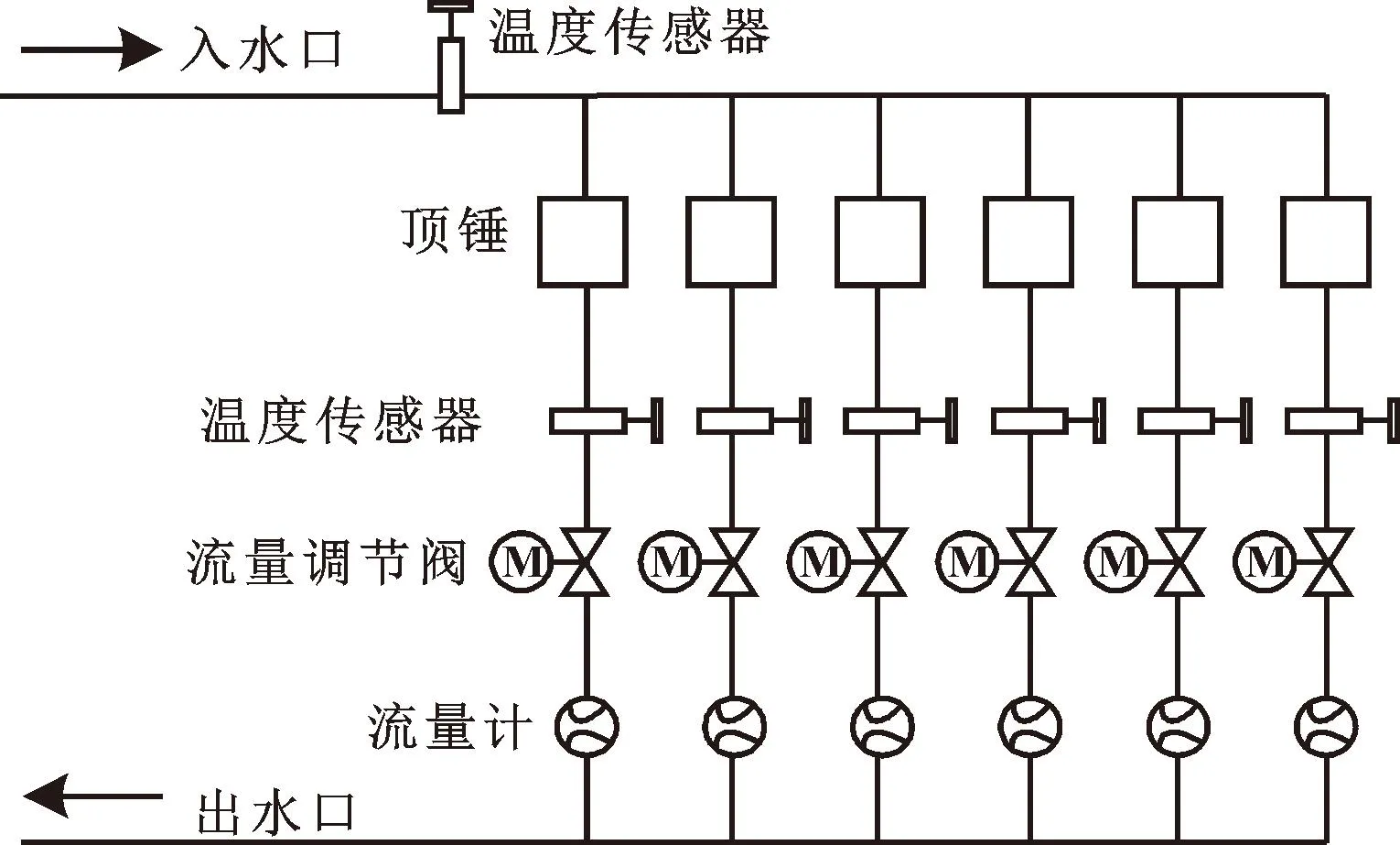
图1 冷却水系统水路原理

1.2 控制原理

如图2所示，上位机设定温度，控制器采集PT100的温度信息，计算出两者的偏差，通过改进WOA-BP-PID算法计算出步进电机的位移量，带动丝杠螺母实现进给运动。当实际温度高于设定温度时，流量调节阀开度增加，降低水温；实际温度低于设定温度时，流量调节阀开度减少，提高水温。

图2 冷却水循环系统控制原理

2 温控系统软件及硬件实现

2.1 总体设计

温控系统总体设计如图3所示，GD32F303主控板调度六路相同的电机驱动控制步进电机，每一路电机使用SPI与主控CPU进行通信，减轻主控板的计算任务量，简化了电路的布线，同时分离式的设计可以方便设备后期的维护与更换。

图3 控制系统框架图

2.2 流量调节阀结构

流量调节阀结构如图4所示，其中阀体上方的步进电机通过销与阀体相连，控制器发出脉冲后驱动步进电机调整流量阀的开度，以改变冷却水的流量，实现精准的温度控制。

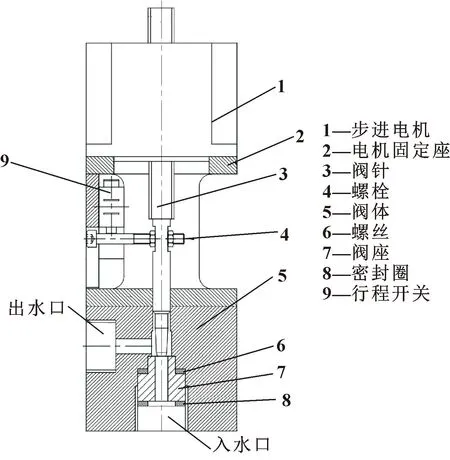
图4 流量调节阀结构

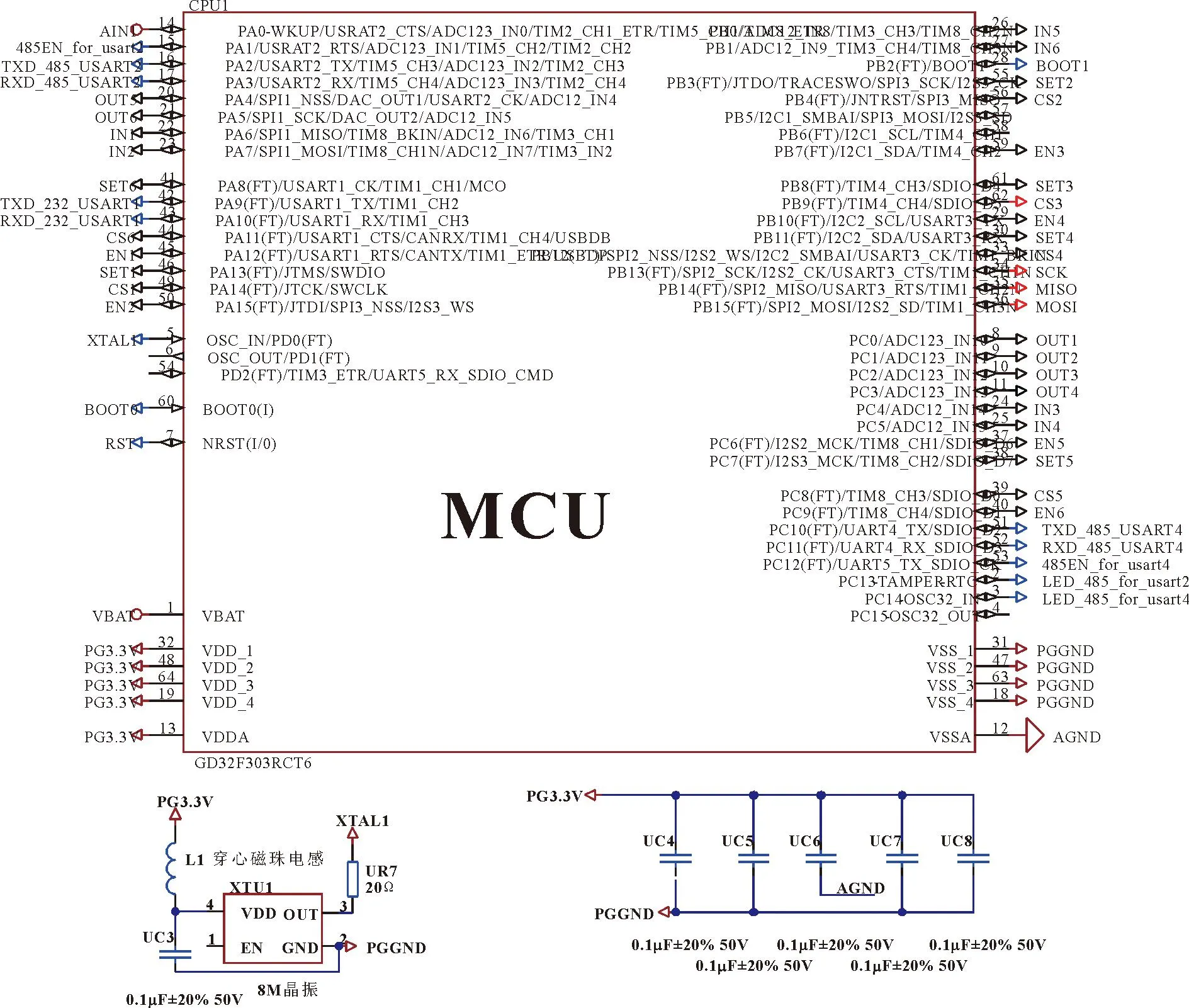
图5 MCU模块电路

2.3 硬件电路设计

控制器以GD32F303为主控制芯片，该芯片计算性能优异，通过外围电路的配合，具有采集实时温度、调控流量输出、故障报警等功能。

控制器和上位机之间采用硬件RS485方式进行串口通信，软件上运用了MODBUS RTU协议，485通信模块的电路如图6所示[9]，A、B差分线上使用3个瞬态抑制二极管，防止浪涌电流损坏通信芯片。

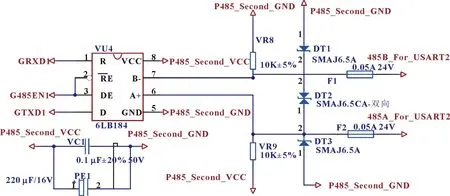
图6 485通信电路

步进电机驱动电路如图7所示，通过驱动电路可以控制步进电机的电流、步数细分、转向等。

图7 步进电机驱动电路

PT100温度采集电路如图8所示，使用AZ432芯片组成一个精密电流源，在PTIN1与PTIN2间接入PT100。当温度变化时，PT100阻值随之变化，同时采用三线制接法及差分运放去除导线电阻的干扰，以保证温度测量的准确性。

图8 PT100温度采集电路

2.4 步进电机运行曲线

步进电机驱动流量调节阀时可分为待机、加速、匀速、减速、停机5种状态，各需要不同大小的驱动力矩，因此需要控制单片机在每个过程输出的电流。电流的大小由以下公式决定：

(1)

式中：VREF是步进电机驱动芯片的脚电压；Rshunt由R5、R6决定。

合理的电机运行曲线能够使电机平稳运行，防止失步和过冲。其中梯形加速曲线算法简单、对硬件资源要求低，且控制系统对速度平稳性要求不高，因此采用梯形加速曲线控制电机[10]。在上位机软件中设定电机运行速度、初速度、加速度、减速度等参数，根据所执行的位移量计算满足梯形曲线的最大加速步数和减速开始步数。当步数达到最大加速步数时，以当前速度匀速运行，当步数达到减速开始步数后，以设定的减速度运行至停止。

2.5 温度采集数据滤波

为保证数据的准确性，减少噪声干扰造成的误差，对采集的温度数据进行滤波处理。采用去极值平均滤波的方法，连续采样n次，去除极大极小值，对剩下的n-2个数据取平均值，公式如下：

(2)

3 温控系统的数学模型

金刚石压机冷却水温控系统可以简化为2个环节：(1)步进电机调整流量调节阀的开度来控制流量；(2)改变循环冷却水流量进行散热。

图4中的流量调节阀可用薄壁小孔模型简化：

(3)

式中：q为输出流量；Cd为流量系数；Δp为入口水流压力；ρ为水的密度；S为流量阀小孔的有效截面积。

流量阀小孔截面积与阀门开度的关系如下所示：

(4)

式中：l为电机丝杆螺母的导程；x为阀门开度；k为阀门开度与转动圈数的系数；θ为流量阀阀芯圆锥角。

将式(4)代入式(3)得到阀门开度与流量的关系：

(5)

实验得到冷却水流量随阀门开度变化的特性曲线如图9所示。

图9 流量与阀门开度特性曲线

此设计采用贯通式步进电机，螺母螺杆置于电机内部，以控制器发出目标开度x作为输入信号，冷却水流量q为输出信号。由图9可知：阀门开度与流量可以看作线性关系，因此此环节简化为比例环节，传递函数如下：

(6)

锤头的热量来源于相控交流加热系统[11]，冷却水从管道入水口流经锤体，换热过程中热量以冷却水为传热介质，与锤头、管道、空气等环境进行换热。因此，以流量阀流量q为输入，冷却水出口温度T为输出。由于热量传递过程具有时滞与惯性，因此温度与流量的输入输出关系可以用一阶滞后的惯性系统来表示，其传递函数为

(7)

式中：t为时间常数；τ为滞后时间；K2为静态增益。

综上所述，系统总传递函数可近似为具有时滞环节的一阶系统：

(8)

式中：G1(s)为开度与流量环节传递函数；G2(s)为流量与温度传递函数。

以循环冷却水的温度为控制变量，将采集到的水温数据上传至上位机，通过MATLAB系统辨识工具箱进行参数辨识[12]，获得系统传递函数如下：

(9)

4 改进WOA-BP-PID控制器设计

4.1 WOA算法

鲸鱼优化算法(WOA)是一种模拟座头鲸捕食行为的元启发式智能算法，模仿座头鲸螺旋捕食的策略，发现猎物后，鲸鱼通过收缩包围、泡泡网捕食、随机搜索猎物3种方式更新自身位置。

(1)收缩包围

座头鲸观察猎物位置，并将其包围，位置更新过程如下：

D=|CX*(t)-X(t)|

(10)

X(t+1)=X*(t)-AD

(11)

式中：X*(t)代表当前最优鲸鱼的位置；X(t)代表当前鲸鱼的位置；A和C为系统系数向量。

其中：

A=2ar1-a

(12)

C=2r2

(13)

式中：a为收敛因子，在迭代过程中由2线性递减至0；r1和r2为0～1的随机数。

(2)泡泡网捕食

座头鲸向猎物的位置收缩包围并螺旋靠近，过程如下：

D*=|X*(t)-X(t)|

(14)

X(t+1)=D*eblcos(2πl)+X*

(15)

式中：b为对数螺旋常数；l在[-1，1]内随机取值；D*为座头鲸与猎物的距离。

收缩包围与泡泡网捕食2种行为同时进行，算法选择以上2种位置更新方式的概率各为50%。引入p，当p<0.5时，鲸鱼收缩包围猎物如式(11)；当p≥0.5时，鲸鱼螺旋靠近，如式(15)。

(3)随机搜索猎物

当|A|≥1时，座头鲸根据各自的位置随机搜索猎物，过程如下：

D=|CXr(t)-X(t)|

(16)

X(t+1)=Xr(t)-AD

(17)

式中：Xr(t)为当前鲸群随机参考鲸鱼的位置向量。

4.2 改进WOA算法

标准WOA算法中，座头鲸进行局部搜索和全局搜索由系统系数A决定，收敛因子a在迭代过程中线性递减，不能很好地平衡局部搜索和全局搜索[13]。在迭代初期，收敛因子应加快下降速率，后期应减慢下降速率，加快寻优过程的收敛速度。因此，提出一种非线性变换的收敛因子：

(18)

式中：tmax是寻优过程的最大迭代次数；t为当前迭代次数。

鲸鱼算法通过式(11)(15)进行局部搜索，为了提高鲸鱼局部搜索能力，加快寻优收敛速度，引入自适应惯性权重参数和随机差分变异策略[14]。

其中自适应惯性权重为

(19)

将式(19)代入鲸鱼位置更新公式(11)(15)得到：

X(t+1)=ωX(t)-AD

(20)

X(t+1)=D*eblcos(2πl)+ωX*

(21)

随机差分变异策略：

X(t+1)=(X*(t)-X(t))r1+(Xr(t)-X(t))r2

(22)

座头鲸收缩包围以及捕食过程利用自适应权重和随机差分变异策略来更新位置，有利于鲸鱼位置的多样性，能够有效地避免陷入局部最优解，加快算法的收敛速度。

4.3 改进WOA-BP-PID控制器

金刚石压机冷却水温度控制的过程具有时滞性、非线性以及时变性，而传统PID控制器对非线性系统的控制并不理想，控制参数无法随系统自适应调整。通过将BP神经网络与传统PID结合，迭代优化出最优参数，但BP神经网络存在收敛速度慢、容易出现局部最优的问题[15]。因此，采用改进WOA算法优化BP神经网络的初始权值系数，实现快速收敛。控制器结构如图10所示。

图10 改进WOA-BP-PID温度控制器

结合冷却水温度控制系统的控制参数，取设定温度rin(k)，温度误差e(k)与实际温度y(k)为神经网络的输入层参数，输出层为PID控制参数Kp、Ki、Kd，隐含层节点个数取为5，故神经网络为3-5-3三层结构，如图11所示。为了加快BP神经网络的收敛，避免陷入局部最小值，采用梯度下降法并增加动量项调整各层网络的权值，BP神经网络性能指标函数为冷却水的温度平方误差[16]。

图11 BP神经网络结构

改进WOA-BP-PID控制策略为：BP神经网络的初始权值系数由改进WOA算法离线训练得到，获得最优的初始权值系数以后，由BP神经网络在线优化实现对PID控制参数的调整。 控制流程如图12所示。

图12 改进WOA-BP-PID控制器流程

5 仿真与试验

5.1 系统仿真

采用改进WOA算法训练得到初始权值系数，设置鲸群规模为30，最大迭代次数为150，适应度随迭代次数变化曲线如图13所示。

图13 适应度曲线

根据冷却水温控系统的特点，选取阶跃函数为系统的输入信号，分别采用传统增量式PID算法、BP-PID算法以及改进WOA-BP-PID算法对冷却水温控系统进行仿真。设定起始目标为45 ℃，55 s后降低为38 ℃，仿真曲线如图14所示。

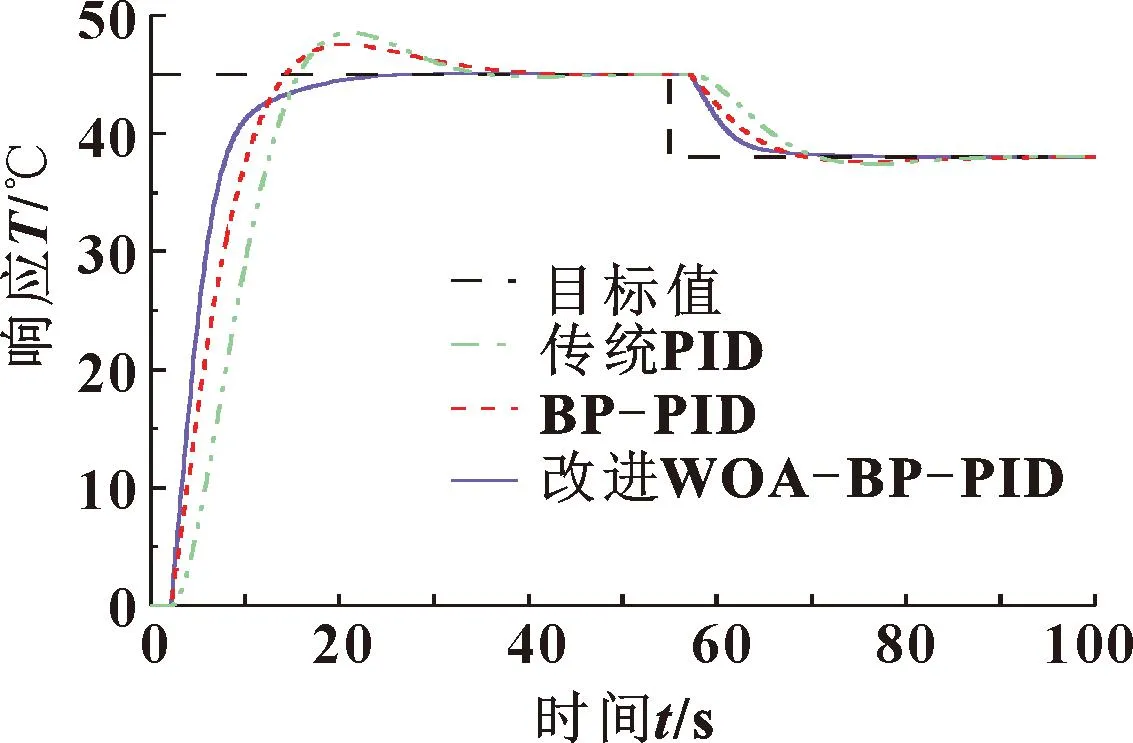
图14 阶跃响应仿真曲线

由图14可以看出：在起始温度阶段，PID、BP-PID、改进WOA-BP-PID控制器的超调量分别为8.2%、5.9%、0.5%，系统达到目标温度所需要的调节时间分别为26.5、23.6、11.5 s。相比传统PID和BP-PID算法，采用改进WOA-BP-PID进行控制时，系统近乎无振荡和超调，能够更快达到稳态，有效提高了控制的快速性与稳定性。

5.2 冷却水温度控制实验

某企业的金刚石压机冷却水温度控制系统六路循环冷却水装置如图15所示。现使用传统增量式PID算法以及改进WOA-BP-PID算法进行冷却水温度控制实验。

图15 六路循环冷却水装置

冷却水温度工艺设定为38 ℃。由图16可知：在冷却水温控系统中，改进WOA-BP-PID算法与人工整定的PID算法相比，超调量更小，且能更快地收敛至目标温度，稳态时的温度误差最大为±0.4 ℃，具有更好的控制精度。

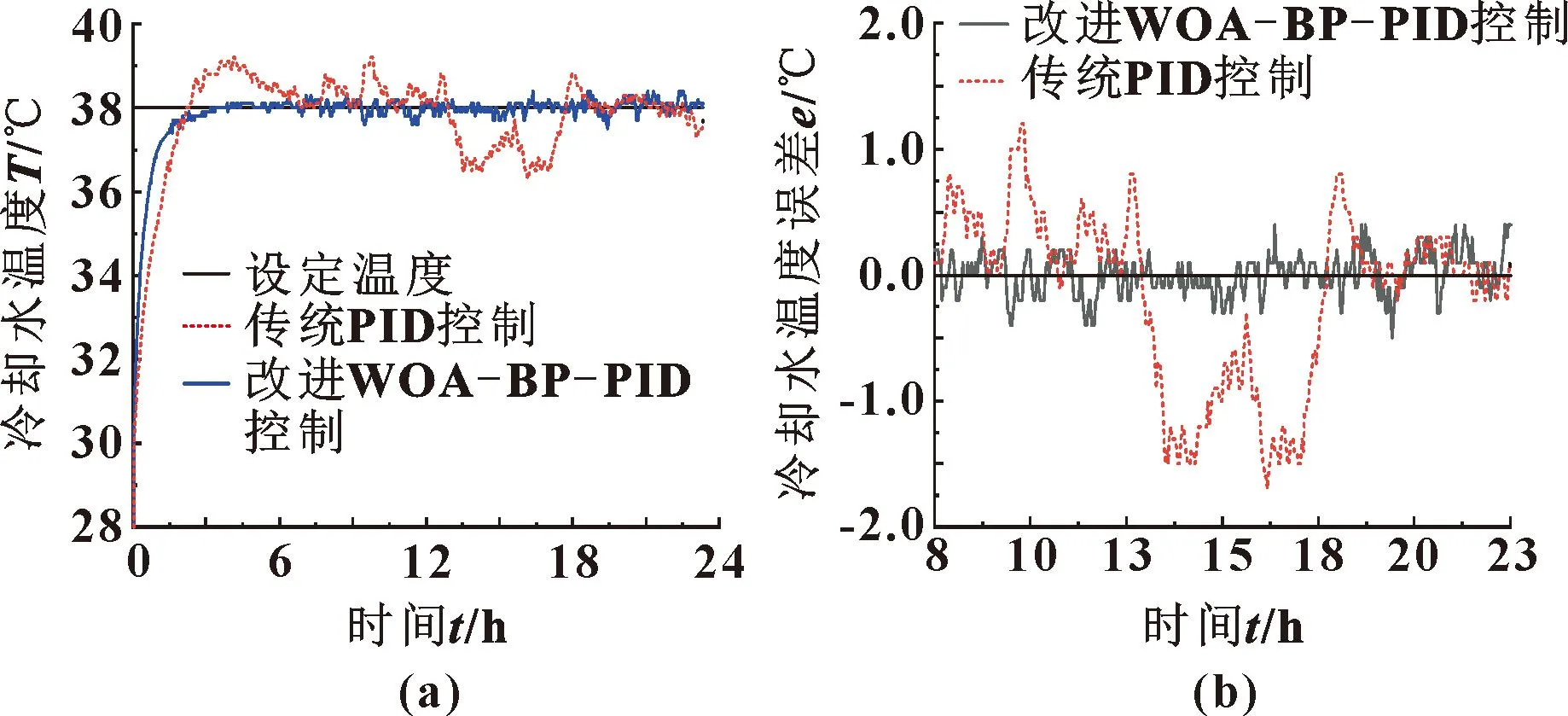
图16 冷却水温度曲线(a)及其误差(b)

6 结论

适宜的冷却水温度是提高金刚石生产品质和延长顶锤寿命的关键，传统PID算法对水温进行控制时存在调整时间长、冷却水温度稳定性不足等问题。因此，文中设计了基于改进WOA-BP-PID算法的冷却水温控系统，在线优化PID参数，同时搭建了硬件电路，通过步进电机调整冷却水流量实现温度的准确控制。仿真和实验结果表明：改进WOA-BP-PID算法实现了PID参数的自适应调整，控制精度更高，能够有效提高冷却水温度控制的效果，保证金刚石生产的质量，在工程上具有一定的实际意义。