基于深度强化学习的多自动导引车运动规划
2024-03-13孙辉,袁维
孙 辉,袁 维
(东南大学 机械工程学院,江苏 南京 211189)
0 引言
近年来,移动机器人仓储系统(Mobile Robot Fulfillment System, MRFS)逐渐在现代物流业中获得了广泛认可[1],以Kiva机器人系统[2]为典型代表的MRFS已在许多世界知名企业(如亚马逊、Gap、Staples、阿里巴巴、京东、顺丰)的物流配送中心得到了大规模应用[1-3]。MRFS采用“货到人”的拣选方式,使用移动机器人或自动导引车(Automated Guided Vehicle,AGV)将存放商品的货架搬运至工作站等待人工拣选,显著降低了传统“人到货”拣选方式下作业人员的劳动强度,并可获得“人到货”拣选方式2~3倍的拣选效率[4]。
大型MRFS中同时执行搬运作业的AGV数量可达数百台[1-2],对AGV行驶路径的规划和运动控制直接影响系统的拣选效率,这里路径规划(path planning)指为每台AGV单独确定一条能够避免与系统中已知静态障碍物(如墙和货架)发生碰撞的最短路径。然而当AGV沿预先规划的路径出行时,碰撞(collision)或死锁(deadlock)等冲突仍有可能发生,这是由于在实际行驶过程中,AGV可能会遇到一些事先未考虑到的动态障碍物,如其他在执行任务的AGV或路过的工作人员[5]。为确保AGV真正实现无冲突行驶,在静态路径规划完成之后,通常需要对系统中的AGV进行协同运动规划(motion planning),并在任务执行过程中对AGV进行及时有效的控制。本文将针对MRFS环境下的多AGV协同运动规划问题展开深入研究。
运动规划是基于冲突预测而对预规划路径进行的验证、确认和修正,目的是为了避免AGV行驶过程中的潜在冲突。一般而言,规避冲突的方法主要分为分区控制(zone control)[6-8]、路径更改[9-12]、速度调整(包括停止等待)[12-14]、行程安排(scheduling)[15-18]4类。分区控制采用限制特定通行区域内AGV数量的方式避免冲突,路径更改则通过使用备选路径或重新规划来规避冲突,这两类方法是为了避免AGV行驶轨迹在空间维度上重叠,而速度调整和行程安排旨在从时间维度上消除AGV发生冲突的可能。
MRFS是一种新型智能仓储系统,从投入实际应用至今只有十余年历史,文献中关于MRFS环境下AGV路径规划和运动规划的研究相当有限。张丹露等[19]为解决AGV路径规划问题提出一种考虑动态加权地图和预约表的改进A*算法,并通过仿真实验验证了该方法的可行性和高效性;ZHANG等[20]和LEE等[21]分别采用改进Dijkstra算法和A*算法进行AGV路径规划,继而在运动规划时通过时间窗预测潜在的碰撞,并针对不同碰撞类型提出使用备选路径、延迟出发、重新规划路径、主动避让等几个可选的防碰撞策略。虽然这些策略的有效性也通过仿真实验得到了验证,但是文中没有明确指出存在多种可行策略时的选择方法。另外,文中也没有详细说明运动规划算法中个别关键参数(如碰撞检测阈值)的设置方法。为解决MRFS环境下的AGV运动规划问题,MAOPOLSKI[22]提出一个基于网格预约占用思想的启发式算法,即在AGV规划路径的每个网格上按照搬运任务先来先服务(First Come First Served,FCFS)原则构建一个AGV预约占用的队列,同时规定AGV必须严格按照队列顺序通行。该算法虽然可以确保实现AGV无冲突行驶,但是单一严格的通行规则也存在柔性不足的问题,可能会增加承担后续任务的AGV的通行等待时间,降低整个AGV系统的作业效率。综上所述,目前针对MRFS环境下AGV运动规划的研究还存在一定局限和不足,不仅需要进一步完善传统规划方法来提高其普适性和灵活性,还需要设计开发基于新思路和新视角的智能规划方法,以充分挖掘MRFS的效率潜力。
本文提出一个新的基于深度强化学习(Deep Reinforcement Learning,DRL)的方法来解决MRFS环境下的多AGV运动规划问题,以探究应用人工智能方法求解此类问题的可行性和有效性。与上述已有研究工作不同,该方法的主要思想是通过集中协同规划AGV车队系统在任务执行过程中的一系列动作决策达到避免碰撞冲突的目的。应用该方法同时为每一台AGV制订其在预规划路径上的行程时间表(schedule),最终得到一个完整的无冲突的AGV运动方案。需要指出的是,文献中尚未发现有使用DRL方法来解决多AGV运动规划问题的研究。
1 MRFS环境中的多AGV协同运动规划
1.1 问题描述
图1所示为一个小型MRFS,该仓储系统地面采用网格(grid)布局。系统中共停放有120个可移动货架,每个货架占用一个单元格,货架间的通道均为双向通道。订单到达系统后,AGV将存放订单商品的货架托举搬运至拣选站,待人工拣选作业完成后再将其运回存储区域。AGV由电池驱动,具有举升和原地旋转功能,利用粘贴在单元格上的二维码进行定位和导航,可以在网格单元间直线行走。另外,空载AGV可以在货架下方自由通行,这意味着接到指令的空闲AGV总是能够沿最短路径赶至目标货架下方,然后开始执行搬运任务。

假设系统中每台AGV的货架搬运任务清单已知,而且每台AGV在执行任务过程中的行驶路径已事先确定。本文多AGV协同运动规划要解决的问题是为每台AGV制订具体的行程时间表,目的是使用“错开出行”策略避免潜在的AGV碰撞,确保其能够在无冲突发生的情况下尽快完成所有货架搬运任务。需要说明的是,这里没有为避免冲突而使用更改预规划路径的传统策略,而是通过在既定路径上为每台AGV设置合理的行程时间表来避免碰撞。这是因为在一个复杂的大型AGV系统中,单纯通过更改路径很难达到杜绝冲突的目的。另外,本文假设系统中所有AGV均保持同一固定速度行驶,不会出现AGV之间的同向追及碰撞问题,这样AGV之间可能发生的碰撞共有相向碰撞、交叉碰撞、停留碰撞3种类型,如图2所示[21]。

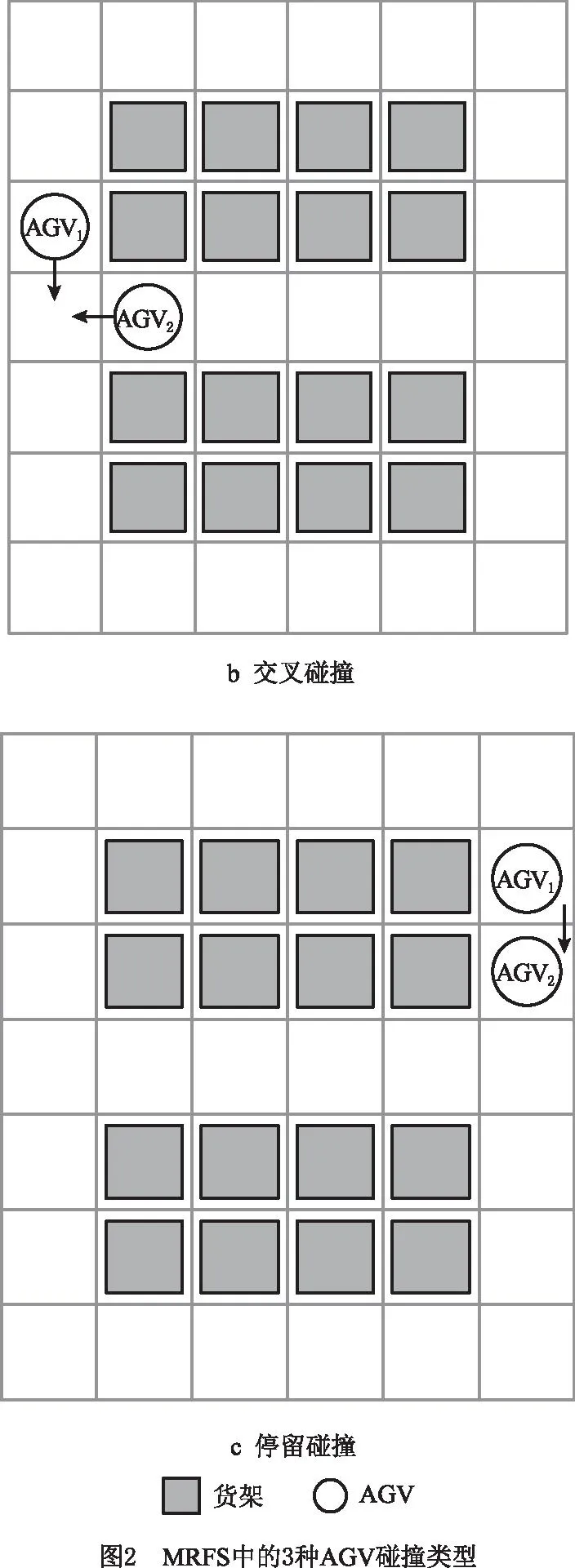
1.2 数学模型
已知在一个MRFS中,共有G台AGV同时执行各自的货架搬运任务。每台AGVg(g=1,2,…,G)的规划路径Pg可用该路径上的单元格编号序列表示,即Pg=(cg1,cg2,cg3,…),这里cgj(j=1,2,3,…)为路径Pg上第j个单元格的编号。假设每台AGV以速度v匀速行驶,将AGV驶过一个单元格的时间视为一个单位时间步(time step),则v在数值上等于单元格的边长。另外,假设在每个单位时间步开始的时刻,每台AGV都恰好完全处于某个单元格内,而且已经为该时间步内将要执行的下一个动作做好了准备,从而可以采用各AGV所处的单元格位置表示AGV车队系统当前的状态。进一步假设车队系统的下一个动作决策只和其当前状态相关,则可以使用一个Markov决策过程(Markov Decision Process,MDP)模型描述MRFS环境下的多AGV协同运动规划问题。下面详细介绍该过程中的状态(states)、动作(actions)、奖励(rewards)和策略(policy)。
1.2.1 状态
在为多台AGV进行运动规划时,需要同时关注MRFS中每台AGV的当前位置。将系统中所有AGV组成的车队视为一个整体,则各AGV在每个时间步开始时所处的单元格位置联合定义了车队的一个状态。以一个5台AGV的车队为例,该车队在某一时刻t的状态st如图3所示。
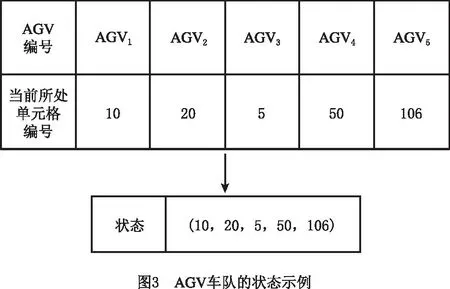
1.2.2 动作
由于假设行驶路径已知且保持不变,在每一时间步开始时每台AGV可选择的动作只有两个,即原地等待或者沿给定路径前进一个单元格,用“0”表示AGV将原地等待,用“1”表示AGV将前行。对于整个车队,将每台AGV的动作决策组合起来构成车队系统的一个动作决策,仍以一个5台AGV的车队为例,车队在某个时刻t将要执行的动作at如图4所示。
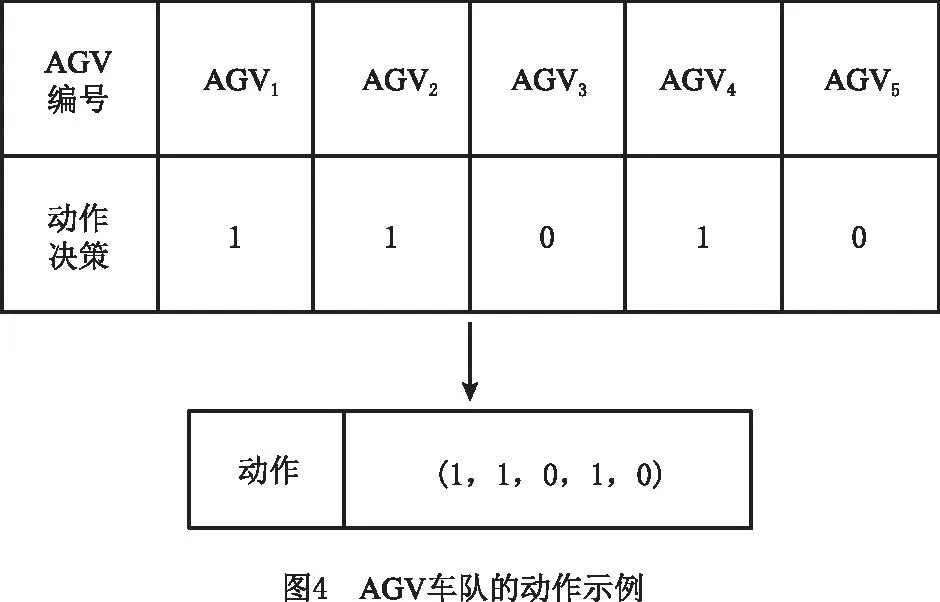
1.2.3 奖励
奖励用以评估车队在某个状态下采取相应动作的优劣程度。令rt表示AGV车队系统在状态st时采取动作at后获得的奖励,rt既和车队中每台AGV所采取的动作相关,又和车队的行驶状况相关,
(1)
式中:rt(g)表示给予第g(g=1,2,…,G)台AGV执行动作的奖励或惩罚,当AGVg沿其既定路径前进时,rt(g)=f(f>0),表示鼓励AGVg按照规划路径前进;当AGVg选择等待时,rt(g)=w(w<0),表示给予其一定惩罚。这样定义rt(g)是希望车队中有更多的AGV同时前行,从而使完成所有搬运任务的时间(即最大完工时间)最短。p表示碰撞引起的惩罚,在执行动作at的过程中,如果发生碰撞,则p=-P(P是一个很大的正数),表示应尽量避免冲突,否则p=0。c是在车队完成全部任务后给予的奖励,当所有AGV都到达其目标位置时,c=C(C为一个很大的正数),表示此时已经找到了无碰撞的协同运动方案,否则c=0。
1.2.4 策略
在MDP中,策略定义了状态和动作之间的映射关系。在每一个时间步的开始时刻t,AGV车队根据一个特定的策略π选择下一个要执行的动作。策略的优劣采用强化学习(reinforcement learning)理论中的动作值函数Qπ(s,a)(也称Q函数)来评估[23]。Q函数指智能体在状态s时采取动作a,并在后续状态转移过程中按照π选择动作获得的期望累计折扣奖励,
Qπ(s,a)=
E[rt+γrt+1+γ2rt+2+…|st=s,at=a,π]。
(2)
式中γ(0≤γ≤1)为折扣因子,用以区分短期奖励和长期奖励。可以看出,AGV车队在未来某一时刻t+i(i=1,2,…)所获奖励rt+i对应的折扣系数γi将随时间的推移而减小。
本文多AGV运动规划的目标即是确定一个最优策略π*,使AGV车队在无冲突的情况下顺利完成所有货架搬运任务,而且可以获得最大的期望累计奖励,即满足
(3)
2 基于DRL的多AGV协同运动规划方法
采用参数为θ的深度Q网络(DeepQ-Network,DQN)作为上述Q函数的逼近器,即Q(s,a;θ)≈Qπ*(s,a)。DQN的概念由谷歌DeepMind团队于2013年首次提出[24],其将反映状态特征的高维原始数据作为输入,在输出端得到每一个状态—动作组合所对应的动作值,因此能够处理具有较大规模和连续状态空间的复杂决策过程。基于DQN的深度强化学习(Deep Reinforcement Learning,DRL)算法已被成功应用于求解多种不同类型的问题,如游戏问题[25]和调度问题[26-27]。
本文提出一种基于DRL的多AGV运动规划方法,其主要思想是将AGV车队系统的状态输入DQN,利用DQN估计该状态下采取每个动作所能获得的最大期望累计奖励。DQN的参数θ经由多次训练后确定,其可为车队选择在一系列连续状态下的最佳动作。DQN训练采用经典的深度Q学习(Deep Q-Learning,DQL)算法[25]完成,并用一个数据集D存储训练过程中的经验数据;另外,用一个与原始网络(也称在线网络)具有相同结构的DQN网络(即目标网络)生成Q函数的目标值,以加强训练的稳定性。表1所示为算法描述中使用的符号和参数。

表1 DQN训练算法中的符号和参数
DQN训练算法的主要流程如算法1所示。每次训练开始时(t=1),每台AGV都位于其各自规划路径的起点。当所有AGV均完成搬运任务并到达终点后,一次完整的训练结束。训练过程中DQN智能体为AGV车队在每一个时间步选择一个动作,执行后车队到达下一状态,该状态转换经验随即被存入数据集D,智能体从D中随机抽取部分经验数据,并用小批量梯度下降法(mini-batch gradient descent)更新在线网络参数θ。当完成预先设定的M次训练后,算法终止运行并输出最终的网络参数θ。下面详细介绍DQN的网络结构、算法的经验回放(experience reply)机制、智能体选择动作所采用的ε-贪婪策略和小批量梯度下降法。
算法1DQN训练算法。
1 初始化经验数据集D的容量N
2 初始化在线网络和目标网络的参数,θ=θ′
3 FOR episode = 1 TO M
4 获取AGV车队初始状态和目标状态
5 FOR t = 1 TO T
6 计算st下的可行候选动作集
7 计算st下所有可行动作的Q值 /由在线网络/
8 选择一个动作at/根据ε-贪婪策略/
9 执行at,获得奖励rt,到达下一状态st+1
10 将转换经验(st, at, rt, st+1)存入D
11 从D中随机抽取b个转换经验(sj, aj, rj, sj+1)
12 计算近似目标Q值yj/由目标网络/
13 对(yj-Q(sj,aj;θ))2执行梯度下降,更新θ
14 每F个时间步,令θ′=θ
15 IF AGV碰撞发生
16 THEN 结束本次训练
17 END IF
18 END FOR
19 END FOR
20 输出网络参数θ
2.1 DQN网络结构
在线网络和目标网络的结构相同且初始参数值相等,分别用于计算Q函数的估计值和目标值。在训练过程中,在线网络不断更新参数θ(即每个神经元节点的权重和偏差),而目标网络的参数θ′相对稳定,在一段时间内保持不变。每隔固定的F个时间步,通过复制当前的在线网络(即令θ′=θ)得到一个新的目标网络。
本文DQN是一个全连接(fully connected)深度神经网络,包括1个输入层、2个隐藏层和1个输出层(如图5)。表2所示为DQN的结构参数,其中输入层的节点数等于AGV的数量,两个隐藏层各自包含64个节点,输出层的节点数为车队可执行的动作总数。仍以一个包括5台AGV的车队为例,网络输入层有5个节点,每个节点的输入信息分别对应其中一台AGV当前所在的单元格编号;输出层有25=32个神经元节点,每个节点的输出为其中一个动作决策所对应的Q值。两个隐藏层的激活函数均为修正线性单元(Rectified Linear Unit,ReLU)。
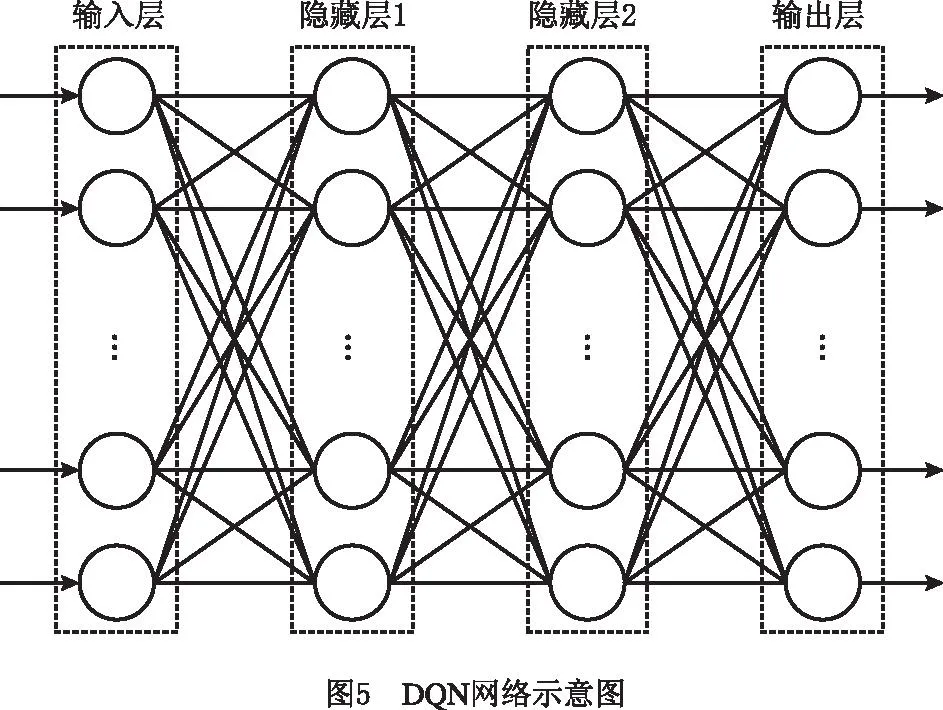

表2 DQN的结构参数
2.2 经验回放机制
经验回放机制指在每个时间步t,将智能体与环境交互得到的状态转换经验(st,at,rt,st+1)存入数据集D。例如,状态转换经验((10,20,5,50,106),(0,1,0,1,1),0.000 5,(10,21,5,51,122)),表示一个包括5台AGV的车队在执行一个动作(0,1,0,1,1)后可以获得的奖励是0.000 5,同时其状态也由(10,20,5,50,106)转换为(10,21,5,51,122)。当经验数据量达到D的容量后,旧的经验将被新的经验取代,从而保证所有训练样本均来自智能体和环境的不断交互。另外,每次更新网络参数时从D中随机抽取固定数量的经验数据,可以满足深度学习对训练数据独立同分布的假设,而且一个经验有机会被多次抽中也提高了数据的利用率。
2.3 ε-贪婪策略
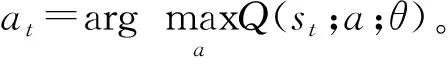
另外,ε随训练次数的增加不断衰减,其数值计算为
ε=εmin+(εmax-εmin)×e-λ,E。
(4)
式中:εmax和εmin分别为预先设置的最大和最小ε值;λε为衰减因子;E为当前累计的训练次数。随着训练次数的增加,ε将从εmax逐渐减小到εmin,表示训练初期以鼓励全局探索为主,后期更加专注于局部开发。
2.4 损失函数与小批量梯度下降
本文用均方差(Mean squared error,MSE)衡量目标Q值与真实Q值之间的差距(即损失),每次迭代时通过最小化均方差损失来训练DQN。第i次迭代时的损失函数Li(θi)定义为

(5)
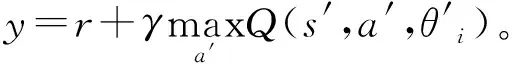
在线网络参数θ的更新采用小批量梯度下降方法,每次从数据集D中随机选择b个样本进行学习。损失函数的梯度
θiL(θi)=
E(s,a,r,s′)[(y-Q(s,a;θi))θiQ(s,a;θi)]。
(6)
3 数值实验
本章通过设计算例验证本文所提AGV协同运动规划算法的可行性和有效性。算例涉及的MRFS仓储系统(如图1)中共包括18×16=288个单元格和120个货架。另外,系统中有一个拣选站,位于第1行第9列的单元格处。假设开始时所有AGV都停放在第1行的泊车单元格内。算例共分为两组,分别用2台和3台AGV执行搬运任务,每台AGV平均承担3~4个任务,平均规划路径长度为120~160个单元格边长,每组算例均包括20个运动规划问题。采用基于DRL的运动规划算法对所有40个算例问题进行求解,并与文献[22]的启发式规划算法进行对比。
在文献[22]中,每台AGV完成任务后就近前往系统中的某个安全停靠点等待。如果其路径终点恰好位于另一台AGV的行驶路径上,则这台处于空闲状态的AGV将成为一个通行障碍,因此在文献[22]算法中加入了终点检测与避让操作,即在每个时间步结束时检查AGV规划路径上的下一个单元格,判断该单元格是否正被其他空闲AGV占用,是则将这台AGV移至附近可用单元格进行避让。
基于DRL的运动规划算法在JetBrains公司的PyCharm平台上用Python语言实现,相关软件及第三方库的版本有Python 3.7.9,tensorflow-gpu 2.0,CUDA 10.0,cuDNN 10.0,keras 2.3.1。文献[22]的启发式运动规划算法在微软公司的Visual Studio 2019平台上用C++语言实现。程序调试和算例求解均在一台CPU主频为1.60 GHz、GPU为NVIDIA GeForce MX250、内存为8.00 GB的个人计算机上完成。
基于文献[23,25-26]推荐和一系列的实验验证,基于DRL的运动规划算法的参数设置如下:M=1 000,N=10 000,F=200,b=128,γ=0.9,εmax=1,εmin=0.1,λε=0.001。DQN训练过程中,每2个时间步进行一次迭代,在线网络参数θ更新时的学习率为0.002。MDP模型中奖励函数的参数f=0.000 5,w=-0.000 1,P=1,C=1。
计算结果表明,对于所有算例问题,基于DRL的运动规划算法均可为车队中的每一台AGV确定其在规划路径上的行程时间表,使得按照时间表运动的AGV车队能够在无碰撞的情况下完成搬运任务。另外,与文献[22]中的启发式算法相比,该算法得到的AGV运动规划方案所需要的平均最大完工时间更短。
3.1 DQN的训练过程
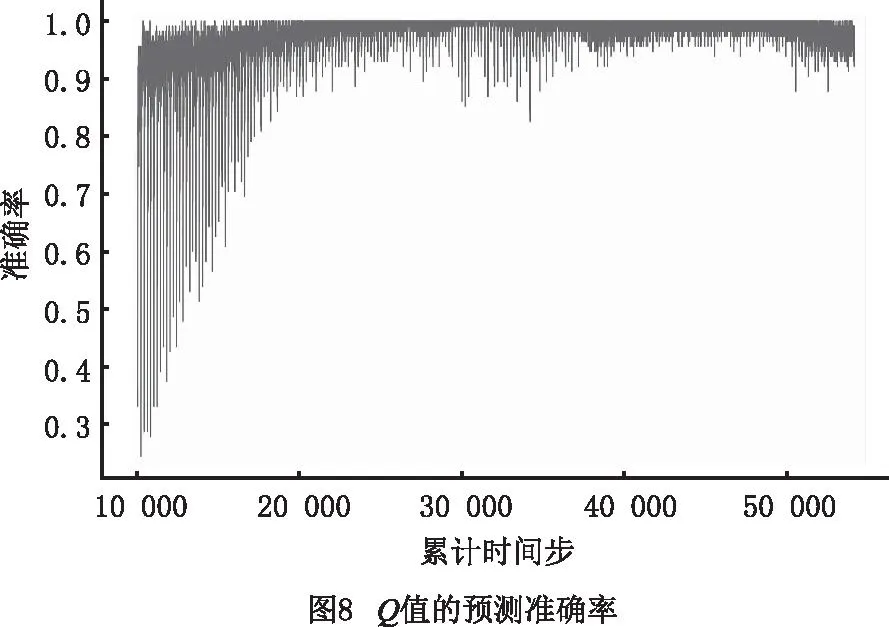
图6~图8所示为DQN训练过程中一些关键指标的变化趋势(以一个包括3台AGV的规划问题为例)。图6中,累计奖励R≈-1表示在训练过程中AGV之间发生了碰撞,导致本次训练提前结束;R≈1表示本次训练最终找到了无碰撞冲突的规划方案。可见,智能体在训练后期找到无碰撞规划方案的频次显著增加。另外,随着累计时间步的增加,DQN预测Q值相对于目标Q值的均方差损失在整体上显著下降(如图7),同时Q值的预测准确率也大幅提高(如图8)。以上指标的变化趋势表明了DQN训练算法的有效性。


3.2 协同运动规划算法的性能验证
由于AGV的行驶速度v恒定(v=1单元格边长/时间步),可用完成全部搬运任务所需要的时间步数(即最大完工时间)作为衡量一个运动规划方案性能的重要指标,时间步数越少,该运动规划方案所需的最大完工时间越短,AGV的搬运作业效率越高。图9和图10所示分别为采用DRL算法和启发式算法求解两组设计算例所得的结果。


由图9可知,对于第1组算例问题,DRL算法和启发式算法求得的规划方案大致相当,所需最大完工时间比较接近,其中DRL算法所得规划方案导致的平均最大完工时间为164个时间步,略少于启发式算法需要的173个时间步。然而在求解效率方面,启发式算法的平均CPU运行时间不到0.1 s,远少于DRL算法5 s的平均运行时间。
由图10可知,对于第2组算例,除了第19个规划问题外,DRL算法求得的运动方案均有显著优势。DRL算法所得运动方案的平均最大完工时间为220个时间步,明显少于启发式算法的253个时间步。可见随着车队规模的扩大,DRL算法的优势更加明显,这可能是因为DRL算法通过智能体的迭代试错能够充分探索问题的解空间,从而有效压缩AGV行驶过程中的等待时间;另一方面,启发式算法自身不具备迭代搜索能力,而且算法要求AGV必须严格按照任务到达的先后顺序占用单元格的通行规则灵活性不够,可能增加承担后续任务的AGV的无效等待时间,最终延长最大完工时间,降低系统整体搬运作业效率。然而在求解效率方面,启发式算法的CPU运行时间仍然远少于DRL算法。
4 结束语
本文针对新型MRFS智能仓储系统中的多AGV协同无冲突运动规划问题,基于AGV“错开出行”的规划策略建立了MDP模型,并设计了基于DQN的DRL算法进行求解。将AGV在系统中的位置输入DQN,输出端可以得到每一可行动作决策的最大期望累计奖励。采用经典的DQL算法训练DQN,训练结束后利用DQN为AGV车队选择行驶过程中一系列连续运动状态下的最佳动作,即可得到每台AGV的最佳出行时间表。算例验证结果表明,应用本文所提DRL算法可以有效求解MRFS环境中的多AGV协同运动规划问题,而且求解质量优于文献中的一种启发式运动规划算法。
本文主要探究了基于DQN的DRL方法对小规模AGV车队进行运动规划的效果,后续将进一步验证其求解大规模车队运动规划问题的性能。另一方面,为提高智能体学习的效率,尝试采用其他DRL方法进行求解,如基于竞争深度Q网络(dueling DQN)的学习方法或融合6种DQN改进的Rainbow学习方法。
