中大口径加榴炮发射环境极限边界工况炮弹引耦合响应特性
2024-03-11田中旺牛兰杰宁变芳马红萍孙诚诚
田中旺,牛兰杰,宁变芳,马红萍,孙诚诚
(1. 机电动态控制重点实验室,陕西 西安 710065;2. 西北机电工程研究所,陕西 咸阳 712099)
0 引言
中大口径加榴炮机械触发引信[1-3]是中大口径杀伤爆破榴弹的主要配用引信,装配数量巨大,在产品交验、部队演训等过程中多次出现弹道炸问题,且历经多轮次的改进设计,弹道炸问题仍未解决[4],其主要原因与中大口径加榴炮高动态发射环境条件下引信响应特性不清晰、失效机理不明确有关。
配用机械触发引信的中大口径杀伤爆破榴弹在火炮发射过程中承受的高动态环境激励主要由发射药燃烧膛压推动弹丸运动过程产生的后坐冲击过载、弹带挤进阻力、弹丸旋转离心过载、弹丸与身管横向撞击力以及出炮口瞬间弹丸轴向、径向约束状态突变导致的振荡冲击过载等耦合构成,其激励水平主要受火炮身管磨损程度、弹丸形态、发射装药量、弹引连接轴线偏离程度等火炮、弹丸、引信的技术状态影响[5-6]。其中,现役中大口径杀伤爆破榴弹弹丸形态主要分为平底弹、底凹弹和底排弹。底凹弹是通过在弹丸底部设置凹陷空腔实现减少阻力增加射程的炮弹。底排弹是通过在弹丸底部设置燃气装置,利用其发射后燃烧产生燃气平衡弹头、弹尾压力差,实现减少阻力并大幅增加射程的炮弹;底排弹发射过程中火药燃烧产生的膛压显著大于底凹弹[7-8]。发射环境中大口径机械触发引信极限边界工况是综合考虑上述影响因素的边界状态,是引信高动态环境响应特性和失效机理分析的重要边界条件。
近些年,国内众多科研人员针对中大口径火炮、弹丸、引信的响应特性开展了研究。文献[9]构建了中大口径加榴炮身管与榴弹耦合非线性动力学响应模型,仿真分析了内弹道阶段弹丸挤进过程与身管的碰撞特性,研究了身管弯曲程度、弹轴偏心情况等因素对碰撞特性的影响。文献[10]构建了身管-弹丸耦合非线性有限元弹塑性模型,分析了弹丸装填情况、装填角状况、摩擦状态、弹炮配合间隙等因素对耦合系统动态响应特性的影响。文献[11]构建了底排弹动态响应模型,通过模态和动力学仿真分析了弹丸固有频率及关键部位响应特性,并对底排弹发射安全稳定性进行了判断。文献[12]针对国内某底排弹在部队训练时出现引信弹道早炸故障,对该底排弹的生产状态及试验过程进行了分析与验证,并通过理论计算,获得引起引信弹道早炸的主要原因可能是小射角装填底排弹不到位。文献[13]主要针对火炮发射装药量、弹丸与火炮身管的配合间隙、弹丸装填到位情况以及火炮身管的磨损情况等底凹弹平台下的独立工况开展了引信典型部位的响应特性和失效分析。文献[14]建立了弹丸与火炮内弹道耦合作用过程动力学响应模型和弹引多刚柔体动力学响应模型,结合随机统计算法分析了引信在弹丸内弹道发射阶段的动态响应特性。上述研究或者从炮弹耦合层面分析了弹炮响应特性,或者以引信及其典型机构在典型工况下的响应特性作为研究重点,对综合考虑火炮身管状态、弹丸形态、弹引连接状态等边界条件的炮-弹-引耦合分析较少,难以高保真地反映引信高动态环境动态响应特性,支撑引信内、外弹道失效机理分析和环境适应性设计。
本文通过建立考虑火炮身管中后期磨损、弹丸形态、弹-引轴线极限偏离等因素的炮-弹-引耦合多级多体动力学弹塑性仿真模型,采用有限元仿真结合试验验证的方式,从内弹道和出炮口阶段弹丸挤进阻力、横向撞击力、姿态角以及引信典型机构过载等参量分布特征,分析发射环境极限工况弹-引典型机构响应特性,为中大口径加榴炮机械触发引信内、外弹道失效机理分析提供支撑。
1 SPH和Lagrange有限元融合算法
国内外关于弹丸膛内运动的分析,大多采用有限元法,理论成熟、计算效率高、数值精度也较高。但是,有限元法是基于网格的数值方法,常规有限元方法(Lagrange)在分析弹带挤进过程大变形时,会出现严重的网格畸变现象,给求解带来很大困难。本文在常规有限元分析方法的基础上,对弹丸在挤进过程中发生大变形的弹带部分采用光滑粒子法(SPH)[15-16]建模;对于身管、弹体和引信等变形较小的区域,则采用Lagrange有限元法建模。
SPH法是一种求解偏微分方程的数值方法,属于无网格法的一种。其核心步骤是:对场函数采用积分近似表示法的核近似过程;对积分近似方程进行离散化的粒子近似过程。
对于任意函数f(x),x为位置矢量,它在解域Ω中可以表示成如下积分形式:
(1)
用函数ω(x-x′,h)来代替式(1)中的δ函数,用f(x)的梯度∇f(x)代替f(x),该函数空间导数的核估计表达式为

(2)
光滑粒子近似过程中,将整个解域离散成一系列任意分布的粒子,物理量的计算只在粒子上进行,因此核估计的积分表达式可转化为粒子求和的离散化形式。假定解域Ω被离散成N个带质量的粒子,粒子j的位置矢量为xj,粒子的体积为ΔVj,粒子的质量为mj,粒子的密度为ρj。因此,在粒子i处的函数值f(xj)的SPH粒子近似式为
(3)
函数f(x)导数的积分表达式(2)可转化为离散化的粒子近似式:

(4)
在固连接触中,SPH粒子定义为从节点,将与SPH粒子接触界面的实体单位表面定义为主表面。如果从节点与对应的主段间有微小的距离存在,则采用正交投影的方法将从节点移动到主表面上。SPH粒子固连在Lagrange单元上的示意图如图1所示。
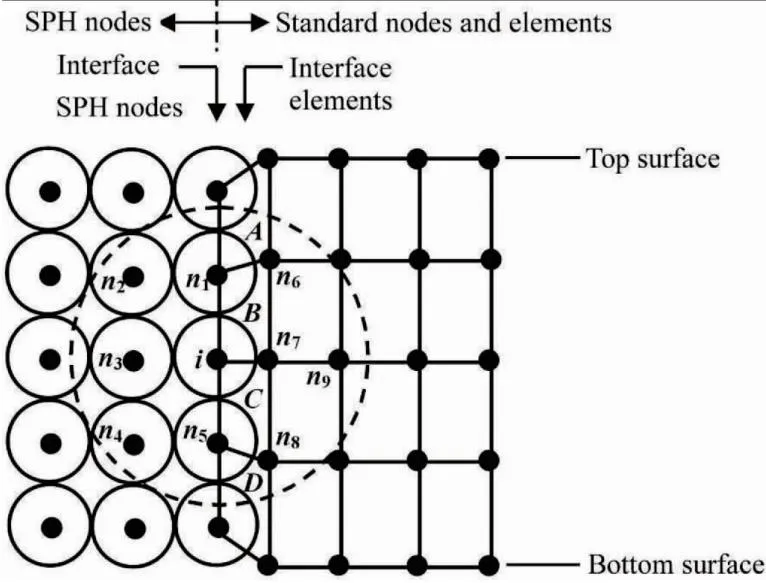
图1 SPH粒子被固连在Lagrange单元上示意图Fig.1 Diagrams of SPH particles being fixedly attached to Lagrange units
固连接触物理量仿真求解过程[17]:对非接触表面的 SPH 粒子及Lagrange单元,从接触表面上节点的已知速度、位移开始,由Lagrange单元的物理量计算相应单元应力、应变率等;由SPH粒子的物理量计算SPH粒子应力、应变率等;在此基础上确定每个 Lagrange单元节点的力、SPH粒子及粒子周围临近节点所受的力;再计算下一时刻所有节点的速度、位移;循环直至完成整个求解时间内的计算。
2.1 有限元模型
以中大口径加榴炮身管、弹丸、机械触发引信、简化后的安全系统结构模型为主体,构建炮-弹-引典型机构耦合动力学仿真模型,如图2所示。

图2 炮-弹-引耦合仿真模型Fig.2 Rifled gun barrel-projectile-fuze coupling simulation model
图2中,身管模型为大口径加榴炮身管混合深膛线模型,弹丸模型分为底凹弹和底排弹模型,引信简化模型由引信体、安全系统、延期装置配重等构成,安全系统模型主要由回转体轴和上、下夹板等构成,榴弹和引信模型均未考虑螺纹连接状态。弹带采用SPH方法建模,固连处理中将弹带 SPH 粒子定义为从节点,将与 SPH 粒子接触界面上的弹体单元表面定义为主表面。
仿真计算主要材料参数如表1所示。

表1 主要材料参数Tab.1 Main material parameters
其中,弹带采用塑性随动强化模型,材料本构关系模型为
(4)

2.2 仿真边界条件设置
约束身管后导向段与摇架后铜衬支撑位置三个方向自由度,约束身管前导向段与摇架前衬套接触位置垂直方向自由度。载荷分别为大口径杀爆弹底凹弹、底排弹0号装药弹底压力设计参数,施加到弹底的载荷曲线如图3所示 。

图3 弹底压力曲线Fig.3 Bottom pressure curve
2.3 仿真工况条件
仿真计算包括重力作用下身管静挠度、弹丸在初始装填速度作用下卡膛过程、弹丸在膛内压力作用下弹炮耦合作用过程等计算步骤。本文主要以弹丸在膛内压力作用下弹炮耦合作用过程为主,对炮-弹-引耦合响应特性进行分析。仿真计算工况主要包括3种,如表2所示。以中大口径加榴炮身管实际使用寿命、底排弹常规发射最大装药量、弹引加工导致的极限偏差,作为极限边界条件的设置依据。极限工况对应的技术状态为:身管中后期磨损、底排弹、0号装药、弹炮间隙2.65 mm、初始装填角0.5°、弹引极限轴线偏差≥0.7 mm、角度极限偏差≥0.3°。

表2 仿真计算条件Tab.2 Simulation calculation conditions
3.1 不同弹丸形态炮弹引响应特性
按照表2中工况1和工况2对应的仿真计算条件,分别以底凹弹、底排弹不同弹丸形态配用相同引信开展动力学仿真。
9 ms时刻底凹弹发射身管、弹带响应云图如图4所示。
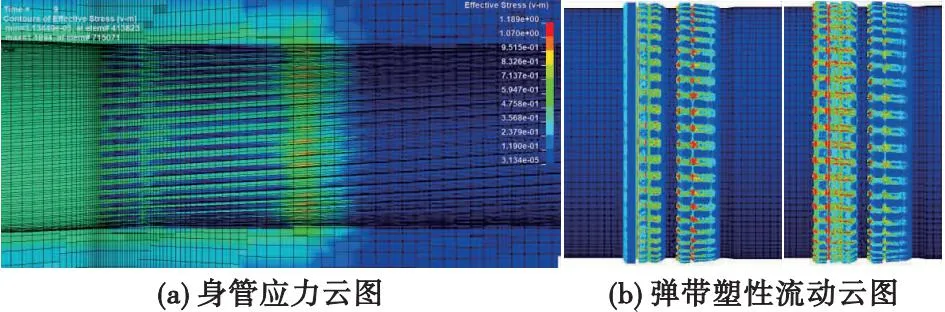
图4 底凹弹发射后9 ms时刻炮、弹响应云图Fig.4 Nephogram of gun-howitzer and projectile response at 9 ms after launching
不同弹丸形态弹丸膛内运动过程挤进阻力对比如图5所示。由图5可知:0号装药相同工况下,底凹弹和底排弹卡膛过程基本一致,约为3.23 ms;弹丸挤进阻力时间历程基本一致,从3.23 ms时刻开始快速攀升,在7.62 ms时达到峰值,弹带刻槽过程结束,随后阻力先快速后缓和下降,在出炮口前挤进阻力消失;底凹弹和底排弹挤进过程峰值分别为685.25和618.86 kN,相差9.69%,差异较小。

图5 0号装药弹丸挤进阻力对比曲线Fig.5 Charge No.0 projectile extrusion resistance contrast curves
不同弹丸形态弹丸前定心部与身管碰撞力对比如图6所示。弹丸前定心部与身管撞击力峰值出现时刻与弹丸挤进阻力时间历程基本保持一致。其中,底凹弹撞击力峰值为9.17 kN,底排弹撞击力峰值为19.6 kN,增大1.14倍。

图6 0号装药弹丸前定心部与身管碰撞力对比曲线Fig.6 Contrast curves of impact force between charge No.0 projectile front centering part and rifled gun barrel
不同弹丸形态弹丸膛内及出炮口阶段运动姿态对比曲线如图7所示。由图7可知:出炮口瞬间,底凹弹俯仰角约为0.039°、偏航角约为0.009°,底排弹出炮口俯仰角约为0.049°、偏航角约为0.016°。
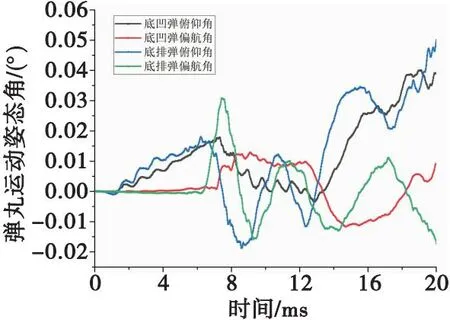
图7 弹丸姿态角对比曲线Fig.7 Contrast curves of projectile attitude angle
不同弹丸形态引信安全系统回转体轴过载响应对比曲线如图8所示。由图8可知:当弹带挤进阻力衰减达到最小时,回转体轴过载峰值基本达到最大;不同弹丸形态引信回转体轴承受的过载脉宽基本一致,峰值差异明显;底凹弹发射回转体轴轴向过载峰值为15 835.58g、径向为3 018.51g,底排弹发射轴向过载峰值为17 944.8g、径向为2 208.15g。

图8 引信回转体轴过载响应对比曲线Fig.8 Overload response contrast curves of fuze rotating body
3.2 极限边界工况炮弹引响应特性
按照表2中工况3对应的仿真计算条件,以身管中后期磨损、底排弹、弹丸最大装填角、弹丸与引信极限偏差等技术状态作为炮-弹-引耦合仿真的极限边界工况,开展动力学仿真。
极限边界工况弹丸膛内运动过程挤进阻力对比如图9所示。由图9可知:极限边界工况下弹丸卡膛时间约为5.43 ms,比常规工况增加2.2 ms;挤进过程的受力情况和时间历程曲线与常规工况差异极大,弹带刻槽过程结束发生在弹丸挤进第一次峰值出现时刻17.53 ms处,对应阻力为493.08 kN;随后阻力衰减,但衰减程度较常规发射工况小,随着弹丸膛内姿态的非稳态变化,出现因碰撞产生的振荡载荷。

图9 极限工况弹丸挤进阻力曲线Fig.9 Projectile extrusion resistance contrast curves in limit boundary conditions
极限边界工况弹丸前定心部与身管碰撞力对比如图10所示。由图10可知:弹丸前定心部与身管撞击力峰值出现时刻与弹丸挤进阻力时间历程基本保持一致;撞击力峰值为584.56 kN,是底凹弹撞击力峰值的63.75倍,是底排弹的29.82倍。
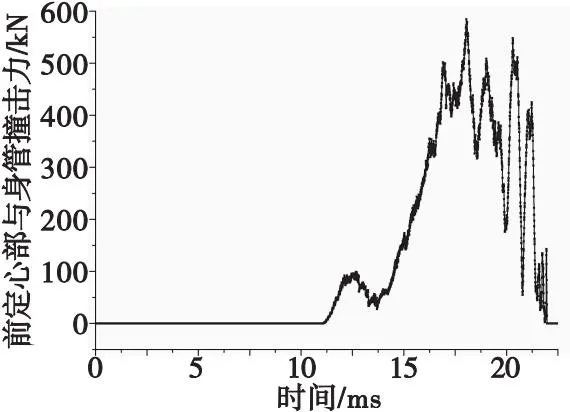
图10 极限工况弹丸前定心部与身管撞击力Fig.10 Contrast curves of impact force between projectile front centering part and rifled gun barrel in limit boundary conditions
极限边界工况弹丸膛内及出炮口阶段运动姿态角变化曲线如图11所示。
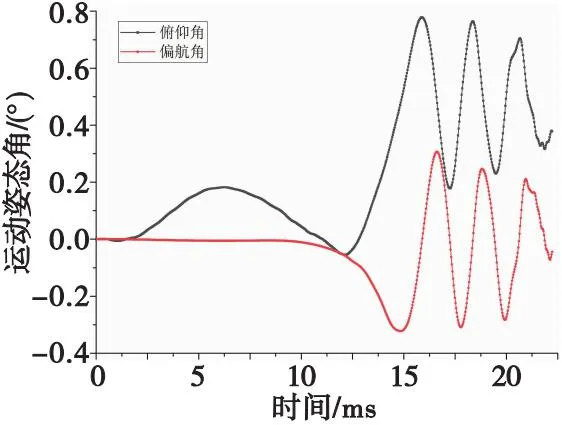
图11 极限边界工况弹丸姿态角变化曲线Fig.11 Contrast curves of projectile attitude Angle in limit boundary conditions
由图11可知:随着弹丸挤进阻力的增大、弹带刻槽深度的增加,弹丸在膛内大幅摆动,姿态角大幅增大,且跟随弹丸挤进阻力的变化产生接近周期性的振荡变化;在出炮口瞬间,其俯仰角为约0.378°、偏航角约为0.044°,相比底凹弹常规工况分别增大8.69倍和3.89倍,相比底排弹常规工况分别增大6.71倍和1.75倍。
极限边界工况引信安全系统回转体轴过载响应曲线如图12所示。

图12 极限边界工况引信回转体轴过载响应曲线Fig.12 Overload response contrast curves of fuze rotating body in limit boundary conditions
由图12可知:回转体轴承受轴向过载峰值出现时刻为15.99 ms,处于弹丸挤进阻力达到第一次峰值上升段,峰值大小为18 921.65g,比底凹弹常规工况增大19.49%,比底排弹常规工况增大5.44%;径向过载膛内出现两次峰值,第二次持续时间较短,属于瞬间碰撞带来的脉冲信号,因此主要分析第一次峰值响应,出现时刻为18.39 ms,处于弹丸挤进阻力达峰后衰减阶段,基本与阻力最小值出现时刻相近,峰值大小为5 394.06g,比底凹弹常规工况增大78.7%,比底排弹常规工况增大1.44倍。
4 试验验证
分别以底凹弹、底排弹0号装药典型工况靶场试验测试得到引信在膛内承受轴向过载峰值作为特征参量,对炮-弹-引耦合动力学仿真响应模型的预测误差进行验证。试验所用火炮为大口径加榴炮,弹丸为大口径底凹榴弹砂弹、底排榴弹砂弹,引信为机械触发引信加装加速度测试采集装置的改装引信,弹引合装时通过调整填砂重量和位置实现试验样机与实际使用弹丸的弹道参数一致。
测试和仿真结果对比如表3所示。可知,基于底凹弹的炮-弹-引耦合动力学模型仿真预测误差为10.91%;基于底排弹的仿真预测误差为10.09%。造成测试和仿真结果误差的主要原因包括:炮-弹-引耦合动力学模型未考虑弹丸发射药燃烧过程;靶场试验测试时火炮身管磨损状态非典型状态;传感器测试本质误差(约1%)难以消除。

表3 测试和仿真结果对比情况Tab.3 Comparison of test and simulation results
5 结论
本文采用融合SPH和Lagrange的有限元计算方法,对考虑身管中后期磨损、底排弹、弹丸最大装填角、弹丸与引信极限偏差等极限边界工况的内弹道环境炮-弹-引耦合响应特性进行了仿真计算和试验验证。基于分析结果可得出如下结论:
1) 极限边界工况对弹丸卡膛时间、弹丸挤进过程承受的阻力以及前定心部与身管撞击力的时域分布特征影响显著。相比底凹弹或底排弹常规发射工况,弹丸内弹道运动过程中,弹带刻槽结束时间延后,弹引遭受的高量值挤进阻力持续时间增大,遭受的弹丸前定心部与身管撞击产生的横向碰撞力最多增大了63.75倍,是导致引信径向过载增大的重要因素。
2) 极限边界工况对弹丸膛内和出炮口阶段运动姿态的影响显著。相比底凹弹或底排弹常规发射工况,弹丸的姿态角幅值和振荡程度明显增大,出炮口瞬间,会以最多增大8.69倍的俯仰角和最多增大3.89倍的偏航角进入外弹道飞行阶段,是导致初始章动角增大的重要因素。
3) 极限边界工况对内弹道阶段引信及其典型机构过载响应影响较大。相比底凹弹或底排弹常规发射工况,引信回转体轴遭受的轴向过载最多增大了19.49%,径向过载最多增大了1.44倍,是导致其强度失效的重要因素。
