基于特征聚类和等距映射的无监督特征选择算法

段立娟, 郭亚静, 解晨瑶, 张文博

(1.北京工业大学信息学部, 北京 100124; 2.可信计算北京市重点实验室, 北京 100124;3.信息安全等级保护关键技术国家工程实验室, 北京 100124)

计算机技术的飞速发展使人们生活在一个万物互联的社会环境中,由于数据来源的多元化,大量高维数据分析已经成为很多领域的重要问题,比如计算机视觉[1-2]、数据挖掘[3-5]和模式识别[6]。

这些海量高维数据中存在着大量的冗余数据和噪声,在进行大数据分析任务时不仅会大大增加计算机的内存负荷和处理时间,而且会降低算法的性能[7-8]。特征选择已经被证实在处理高维数据方面是有效且高效的。

近年来,无标签场景下的特征选择引起学者们的广泛关注。无监督特征选择方法根据选择特征的策略可分为过滤方法、包装器方法、混合方法3种主要方法。

1)过滤方法根据数据的内在属性评估特征。He等[9]提出拉普拉斯分数(Laplacian)方法是最经典的过滤方法之一。它根据保留原始数据固有结构的能力,分别计算每个特征的Laplacian,特征分数越小其局部保持力就越强,越有代表性。Du等[10]提出的矩阵分解鲁棒无监督特征选择方法(robust unsupervised feature selection via matrix factorization,RUFSM)可以在某范式下同时进行鲁棒判别特征选择和鲁棒聚类,同时保留数据的局部流形结构。Tang等[11]提出一种通过对偶自表示和流形正则化(dual self-representation and manifold regularization,DSRMR)进行鲁棒无监督特征选择的有效方法。

2) 包装器方法使用特定聚类算法的结果评估特征子集。Guo等[12]提出与嵌入式无监督特征选择(embedded unsupervised feature selection,EUFS)[13]相同的目标函数,其不同之处在于最终模型的损失函数采用Frobenius范数代替l2范数,采用K均值聚类算法更新参数迭代进行,直到模型收敛。Guo等[14]提出的依赖引导式无监督特征选择(dependence guided unsupervised feature selection,DGUFS)能够同时执行特征选择和基于l2范数的约束模型聚类。

3) 混合方法[15-16]试图综合过滤器和包装器的质量,在效率和有效性之间达成良好的折中。Li等[17]利用非负谱分析获取更准确的聚类标记指标,同时将聚类标记与特征选择矩阵实现联合迭代学习,给出全新的特征选择算法——非负判别特征选择(nonnegative discriminant feature selection,NDFS)。Yang等[18]给出的无监督判别的无监督算法(unsupervised discriminative feature selection,UDFS)把判别分析和l2,1范数最小化结合形成联合框架,优化计算筛选出在批处理的模式下最具辨别力的特征集合。UDFS、NDFS方法仅集中于鉴别特征的选择,这是聚类或分类问题中的主要作用。然而,这些方法没有考虑所选择特征的高相关性,对聚类或分类结果具有不利影响。为了选择具有低冗余度的特征,Cai等[19]提出的多簇特征选择(multi-cluster feature selection,MCFS)算法考虑数据内在的流形结构利用谱分析进行学习,可以更好保留特征的多簇结构。谢娟英等[20]给出基于标准差的谱聚类无监督特征选择方法(feature selection by spectral clustering based on standard deviation,FSSC-SD),通过谱分析方法对各种特征属性进行聚类,然后定义特征重要度评价指标为特征独立性与特征区分度之积,从各聚类类簇中找出重要度最大即最具代表性的特征加入特征子集。

本文通过对类簇中的特征进行等距映射和稀疏学习打分,可以更好地保留数据原始流形结构,促进类簇中价值信息的表达,进而可以选择出该类簇的高代表性的强分类特征,提升准确率。

1 FSFCI算法

本文针对无标签场景下特征选择方法大多无法很好兼顾到分析结果的准确率和稳定性的问题开展研究,提出新的特征选择算法——基于特征聚类和等距映射的无监督特征选择算法(unsupervised feature selection algorithm based on feature clustering and isometric mapping,FSFCI)。

具体的算法架构见图1,主要分为等距映射特征聚类簇、学习稀疏系数向量、代表性特征选择3个模块。

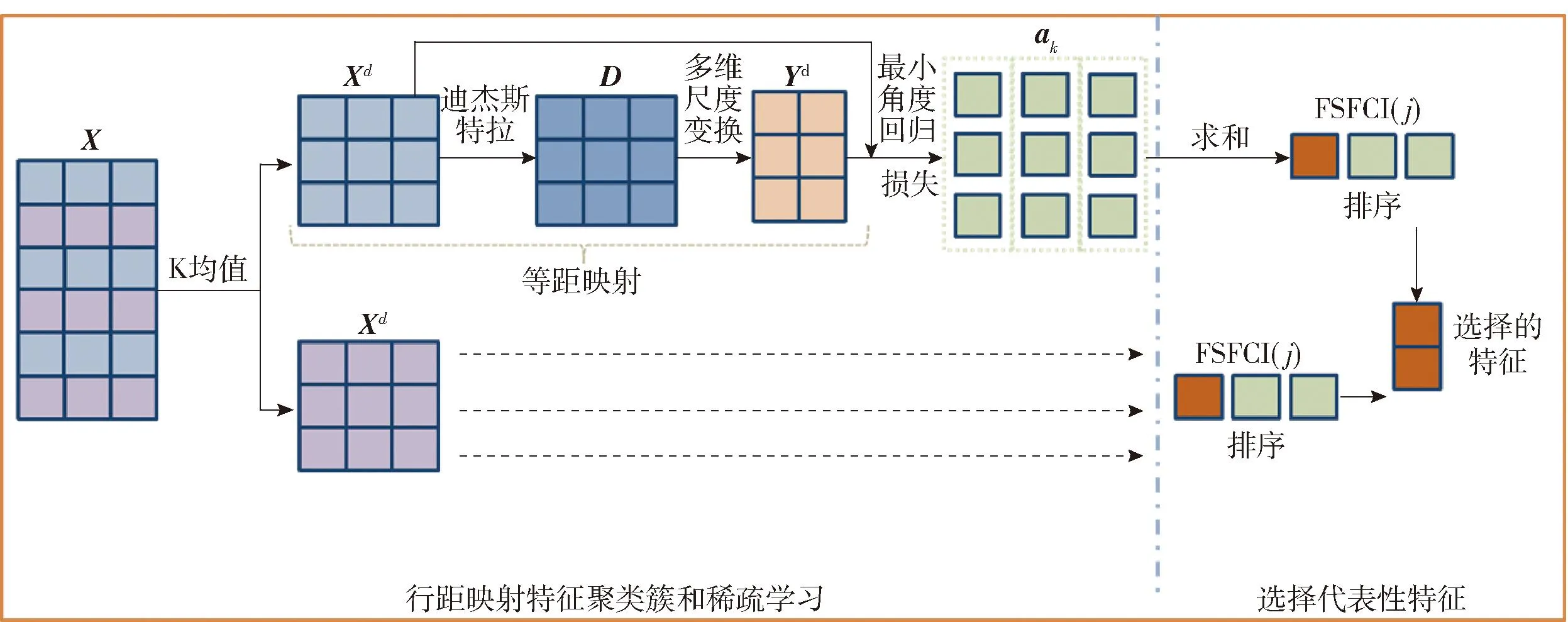
图1 算法流程Fig.1 Algorithm flow

等距映射特征聚类簇模块首先基于特征的相关性将数据集X的特征通过K均值聚类聚成d个类簇Xd,然后通过等距映射(isometric mapping,ISOMAP)方法使Xd形成高维数据的低维嵌入表达Yd。在ISOMAP算法中,首先通过迪杰斯特拉(Dijsktra)算法计算K邻接图中样本点之间最短路径来构建距离矩阵D,然后调用多维尺度变换(multiple dimensional scaling,MDS)算法得到类簇的低维表示Yd。

学习稀疏系数向量模块通过构建Xd与Yd的线性回归模型对系数矩阵进行优化,使用具有基数约束的最小角度回归(least angle regression,LARs)算法解决l1正则化回归问题,从而学习到稀疏系数矩阵ak,ak代表了Xd与Yd的相关程度表示第k个特征的重要性。

代表性特征选择模块将各个特征的稀疏系数根据重要度评分函数FSFCI(j)加和排序后,选出该类簇中分数最大的特征作为该类簇的代表性特征加入特征子集中,最终d个类簇形成具有d个代表特征的特征子集。

1.1 等距映射特征聚类簇

学者们已经提供了许多流形的降维算法。这些方法可以通过对数据的整体构造和几何构造来分解数据并实现降维,由欧氏空间转换到流形空间,最后得到和数据几何构造保持一致的低维嵌入表示。本文的特征选择算法是先利用ISOMAP算法来学习对高维数据的低维嵌入,它是一个能够有效掌握高维数据内在几何构造特征的流形学算法。

首先根据特征之间的相关性进行聚类,把具有强依赖性的特征聚成d个类簇,每个类簇中有dk(k=1,2,…,d)个特征。本文对各个类簇中样本数据使用ISOMAP算法。由于ISOMAP算法中采用了MDS降维,因此能最大限度地保持数据点的内在几何结构,即保持两点间的测地距离。首先计算出样本点之间的欧氏距离矩阵,构建邻域关系图G(V,E),对每个xi(i=1,2,…,N)采用K最近邻(K-nearest neighber,KNN)算法计算其p近邻xi1,xi2,…,xip,记为Nj,以点xi为定点,欧氏距离d(xi,xij)为边,建立邻域关系图G(V,E)。传统的计算测地距离D=(dij_)n×n,在G(V,E)中寻找最短路径,公式为

(1)

接着对D=(dij)n×n运用MDS方法降维,从而将原始高维的样本数据用更低维的特征向量来加以表达,实现了流形空间与其对应低维空间之间的映射关系,并由此得到对应的高维数据的低维嵌入表达Yd来完成特征选择。

1.2 学习稀疏系数向量

在1.1节得到类簇中样本数据的低维嵌入Yd的基础上沿着每个内在维度(Yd的每个列)来评估每个特征的重要性。给定一个yk,通过最小化公式的训练损失来指导获得一个相关的特征子集。

(2)

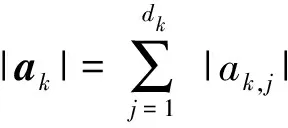
式(2)中的回归问题,其等效公式为

(3)

LARs算法可用于求解式(3)中的优化问题。LARs通过指定ak的基数(非零条目数)来控制ak的稀疏性,而不是设置参数γ,这对于特征选择特别方便。

1.3 代表性特征挑选

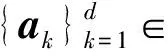
(4)

式中ak,j是向量ak的第j个元素。然后,本文按照FSFCI分数降序排列所有特征,并选择每个类簇中评分最大特征作为代表特征,形成特征子集。

1.4 算法思想描述

FSFCI算法描述如下。

输入:N个具有M特征的数据样本X;最近邻数p;LARs基数约束γ。

输出:选择的d个特征。

开始

1) 等距映射特征聚类簇

① 根据特征的相关性做K均值聚类,使特征聚成d个类簇Xd。

② 对每个类簇进行ISOMAP降维得到数据的低维嵌入表示Yd。

2) 学习稀疏系数向量

① 类簇中建立Xd与Yd的线性回归模型,即式(2)。

② 使用基数约束为γ的LARs算法解决式(3)的l1正则回归问题,得到稀疏系数矩阵ak。

3) 代表性特征挑选

① 按照式(4)计算每个类簇中各特征评分并降序排列。

② 选出每个类簇中评分最大的特征作为代表特征,形成特征子集。

END

2 实验

2.1 数据集

实验选择了14个公开数据集对算法进行测试研究,实验数据集可以从Feature Selection Datasets,Cancer Gene Expression Data Sets数据库获取,数据集的详细信息见表1,其中, warpAR10P、warpPIE10P、YaleB和Yale是人脸数据集,COIL20是实物数据集,GLIOMA、lymphoma、Prostate-GE和Lung-discrete是生物数据集, RELATHE和PCMAC是文本数据集,Umist和USPSdata_20是手写数字数据集,Isolet为音频数据集。

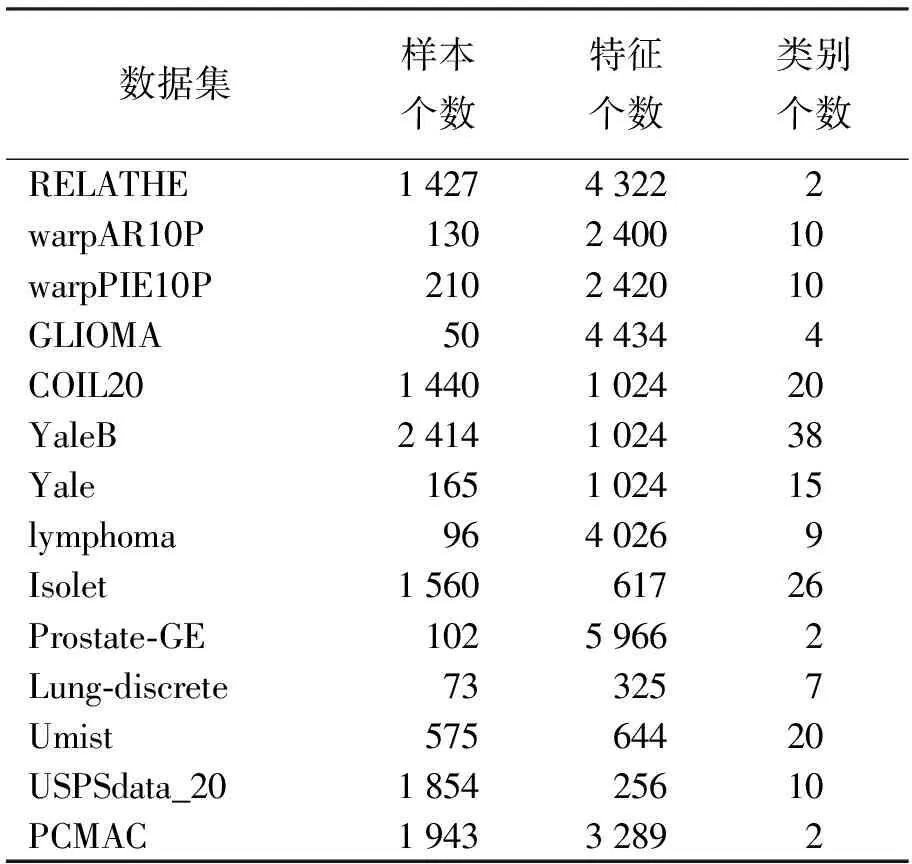
表1 实验数据集描述

2.2 参数设置

为了检验所提出的FSFCI算法的性能,实验比较了FSFCI算法与其他无监督特征选择算法在选择2～100个特征(步长为2)以及选择所有特征时的实验结果。用作对比的算法包括经典Laplacian[9]、MCFS[19]、NDFS[17]、UDFS[18]和较新的FSSC-SD[20]。

本算法实验中均采用欧氏距离计算特征间距离,采用热核相似性度量特征间相似性,近邻数p设置为5,带宽参数t设置为1。NDFS方法的参数γ设置为108,α和β均设置为1。UDFS算法将正则化参数设定为0.1。

对于所有的实验数据集,特征选择的个数设定为{2,4,6,…,100},采用KNN算法对数据集进行了分类,KNN算法中参数设置p=5。采用十折的交叉检验方式划分训练集与实验集,并采用最大最小化的方式对数据进行标准化。每组实验进行5次十折交叉验证,选取5次结果的平均值作为实验结果来比较各算法的性能。

2.3 评价标准

评价标准指标包括分类准确率、受试者工作特征曲线下面积、准确性与召回率的调和平均数。分类准确度表示所有样本中完全划分准确的比率。受试者工作特征曲线下面积表示预测的正例排在负例前面的概率。准确性与召回率之间的调和平均数,只有在准确性与召回率都非常高时,其值才会高。上面的3个指标的值越大,说明算法效果越好。

2.4 实验结果分析

本文对比了所提出的FSFCI算法与其他5种无监督特征选择算法FSSC-SD[20]、Laplacian[9]、MCFS[19]、NDFS[17]及UDFS[18]特征选择的性能效果,并对性能指标值进行了综合分析。

表2为最大分类准确率数据,表3为各算法在最大分类准确率时所选特征子集数量数据。其中最优结果用粗体表示,次优用下划线标注。

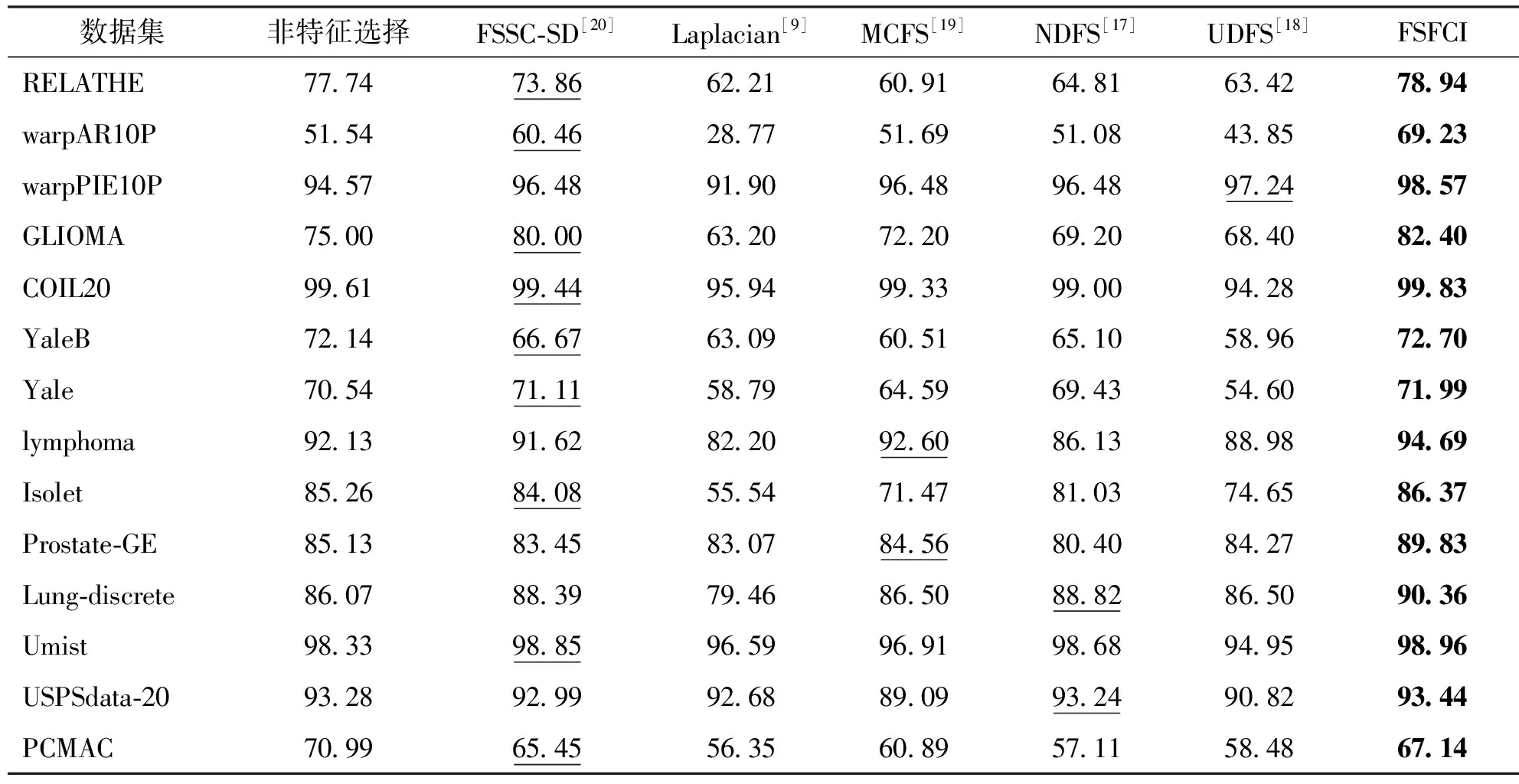
表2 比较算法的最大分类准确率

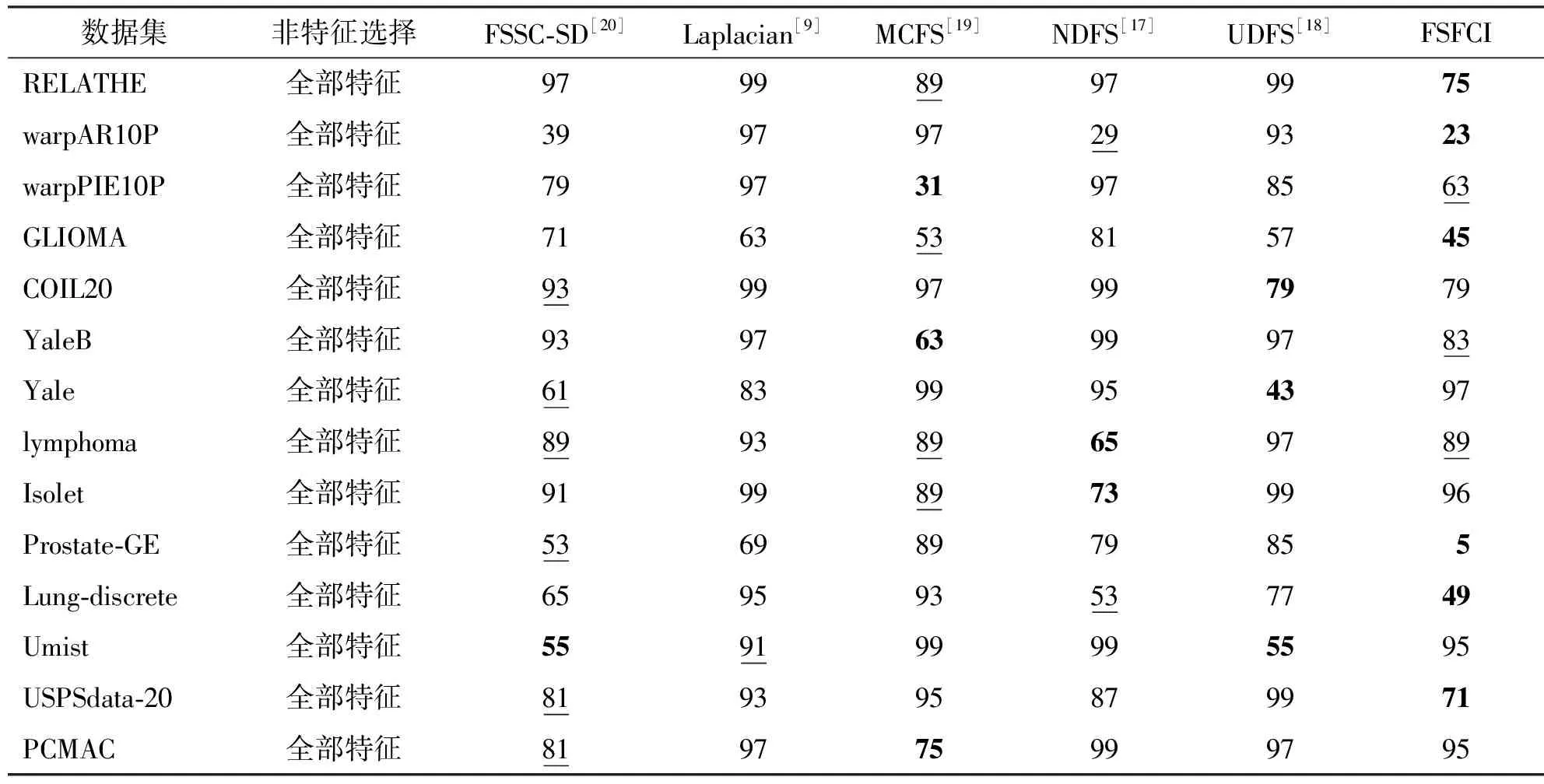
表3 最大分类准确率时所选择的特征数量

1) 准确率对比

表2揭示了无监督特征选择算法不但可以大幅减少特征维度,还可以提高分类准确率。尤其是所提出的FSFCI算法,它的最大分类准确率与其他算法相比较都获得最高水平,且平均最大分类准确率能提高2.97%～13.19%,证明了FSFCI算法中选取的特征子集更具有效性和代表性。

2) 最大分类准确率时选择特征数对比

表3显示了数据集通过特征选择,可以选择出远少于原始特征维度的并且具有强分类能力的特征。尤其是本文提出的FSFCI算法,在保证最大分类准确率的基础上,平均选择特征数最少为69,体现了本算法特征选择的良好性能。

3) 部分结果可视化展示

图2是各算法在warpAR10P数据集上进行特征选择后的实验结果。可以看出,FSFCI算法的各项指标值都显著高于其他比较算法,FSSC-SD[20]算法次之,紧随其后的是UDFS[18]、MCFS[19]和NDFS[17]算法,Laplacian[9]算法在此数据集中表现的效果最差。FSFCI算法在选择特征数为23时,分类准确率达到最高,且FSFCI算法选择特征数多于20之后,各项指标值均最高。但随着选择特征数的增加,FSFCI算法指标值有些许下降趋势,分析原因为随着选择特征数的增加,选择了更多的冗余和混杂的特征,导致效果有所下降。

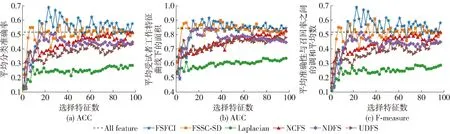
图2 warpAR10P数据集特征选择结果对比Fig.2 Comparison of warpAR10P data set feature selection results

图3是各算法在RELATHE数据集上进行特征选择后的实验结果。可以看出,FSFCI算法的各项指标值都显著高于其他比较算法,FSSC-SD[20]算法次之,紧随其后的是UDFS[18]和NDFS[17]算法,MCFS[19]和Laplacian[9]算法在此数据集中表现的效果较差。FSFCI算法在选择特征数为75时,分类准确率达到最高,且FSFCI算法在选择特征数多于20后,各项指标值均超过其他算法。随着选择特征数的增加,该算法的各指标值均平稳增加,体现了本算法的良好性能。

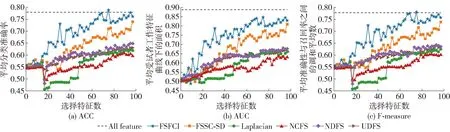
图3 RELATHE数据集特征选择结果对比Fig.3 Comparison of RELATHE data set feature selection results

图4是各算法在GLIOMA数据集上进行特征选择后的实验结果图。可以看出,FSFCI算法的各项指标值都显著高于其他比较算法,FSSC-SD[20]和MCFS[19]算法次之,紧随其后的是UDFS[18]和NDFS[17]算法,Laplacian[9]算法在此数据集中表现的效果最差。FSFCI算法当选择特征数为45时,分类精确度获得最高。随着选择特征数的增加,FSFCI算法指标值也有些许下降的趋势,分析原因为随着选择特征数的增加,选择了更多的冗余和混杂的特征,导致效果有所下降。

图4 GLIOMA数据集特征选择结果对比Fig.4 Comparison of GLIOMA data set feature selection results

图5是各算法在COIL20数据集上进行特征选择后的实验结果图。可以看出,FSFCI算法的各项指标值都显著高于其他比较算法,FSSC-SD[20]、NDFS[17]和UDFS[18]算法次之,MCFS[19]、Laplacian[9]算法在此数据集中表现的效果较差。FSFCI算法在选择特征数为79时,分类准确率达到最高,且FSFCI算法在选择特征数多于15后,各项指标值均已经超过其他特征选择算法的结果。

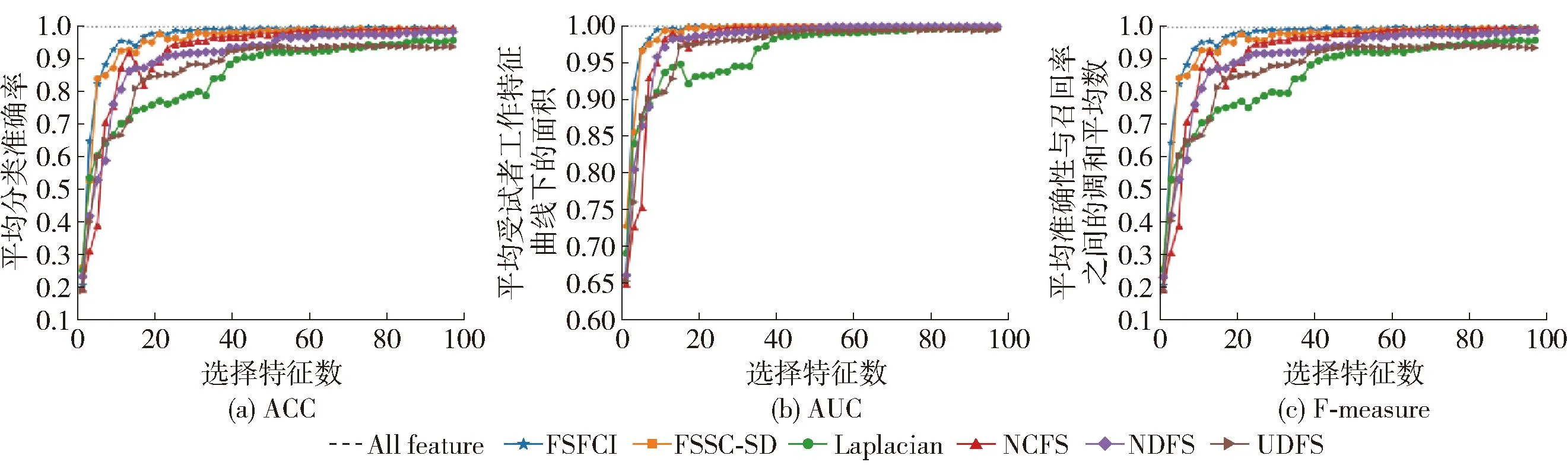
图5 COIL20数据集特征选择结果对比Fig.5 Comparison of COIL20 data set feature selection results

综合实验结果来看,FSFCI算法能够选择出具有强分类能力的特征子集,有效地提升实验的分类准确率,并且有很好的泛化能力。

3 结论

1) 本文针对无标签场景下特征选择方法大多无法很好兼顾到选择结果的准确率和稳定性的问题,提出了面向高维多源数据集的FSFCI算法,算法根据等距映射定义新的特征得分函数,为各特征簇中特征进行打分,挑选类簇中得分最高的特征作为代表特征。实验结果表明,FSFCI算法可以取得比经典流行的FSSC-SD[20]、Laplacian[9]、MCFS[19]、NDFS[17]、UDFS[18]更好的效果,尤其是准确率提升明显,说明它对高维数据具有较好的处理能力。同时在多个高维数据集上的良好表现,表明了FSFCI算法对数据集的依赖性较小,因而具有一定的普适性。

2) 本文提出的FSFCI算法在多种高维特征数据集上均有很好的效果,但是仍存在可以改进的空间。一方面可以从提高算法的最大分类准确率和减小算法的时间成本2个方向进一步优化算法。另一方面,由于现有的大多数基于聚类的特征选择技术都需要额外指定选择特征的数量以及大量的参数,而实际中,无法确定每个数据集所对应的最优选择特征数量与最适参数,因此可以在自适应的方向做进一步研究。