基于时空认知膨胀卷积网络与多源影响因素的PM2.5细粒度预测模型

刘希亮, 赵俊杰, 张羽民, 林绍福, 李建强, 梅 强

(1.北京工业大学软件学院, 北京 100124; 2.集美大学航海学院, 厦门 361021)

由于城市工业化的影响,空气污染逐步成为一个严重的社会问题。据统计,中国每年因空气污染物致死大约为100万人[1]。被称为PM2.5的可吸入颗粒物已成为全球城市严重空气污染的核心指标。人类长期暴露在高浓度PM2.5中会显著增加患病风险,使人体自身呼吸系统、神经系统、心血管系统及生殖系统遭受严重损害[2]。国际癌症研究机构(International Agency for Research on Cancer,IARC)将PM2.5列为第一类致癌物[3]。如何对PM2.5浓度进行细粒度精确化预测,已成为大气环保和公众健康的重要研究课题。

本文分析了近几年PM2.5预测方面的研究文献,认为一个具有良好预测性能的预测模型应该满足以下条件:1) 需要考虑大气污染物和气象因素对PM2.5扩散演化过程的重要影响。大量研究将监测站点的大气数据纳入PM2.5预测建模,这些大气数据主要包括气象因素(大气压、温度、湿度、风向等)和空气污染物(PM2.5、PM10、CO、NO2等)。2) 需要将监测站点间时空相关性纳入模型构建。受诸多时空影响因素制约,目标站点与周边站点的PM2.5序列在空间和时间维度上相互依赖。如何有效捕获站点间的时空相关性,是提升预测精度的关键所在。

目前,PM2.5预测的创新工作倾向于采用数据驱动方法,从PM2.5时间序列中挖掘时空依赖特征。在时间特征提取方面,循环神经网络(recurrent neural network, RNN)[4]及其变种模型是当前主流时序建模方法。然而,这些基于RNN的序列方法存在反向传播耗时、梯度爆炸和梯度消失的问题[5]。在空间特征提取方面,图卷积网络(graph convolutional network, GCN)和卷积神经网络(convolutional neural networks, CNN)具有优异的性能。GCN将CNN从欧氏空间数据推广至非欧氏空间数据,能够融合图的结构属性和节点特征信息进行模型构建,从中提取拓扑图的空间特征[6]。然而,当前图模型仍具有一些局限性,如人为定义变量间的相互关系、节点之间缺失连接等均加剧了模型性能的退化[6]。图卷积模型难以稳定地捕捉动态时间序列之间的连接关系(连接关系表示节点间一些动态的空间交互特征)。在近期研究中,CNN也被广泛运用于提取PM2.5的空间分布特征[7]。CNN可以通过卷积核捕获局部感受野的空间信息,通过多层卷积和池化获得全局空间特征,并且具有并行计算和梯度稳定的优势[6-7]。基于CNN的模型为PM2.5浓度预测开辟了新的研究方向。认知计算[8]从模拟人类认知模式出发,填补了当前智慧城市建设的连贯、统一、普遍机制空白[9],也为细粒度空气质量预测的发展提供了一条可行之路[10]。

针对当前研究的不足,本文在建模过程中融入认知计算架构,融合时空相关性特征、空气污染物和气象因素,提出了一种基于时空认知膨胀卷积网络(spatial-temporal cognitive dilated convolution network,ST-C-DCN)的细粒度PM2.5预测模型。在时间依赖性提取中,本文采用的堆叠膨胀卷积,具有简洁的模型架构且很少出现梯度问题的优势,且能从时序数据中提取长时、有效的时间依赖特征,克服了传统RNN模型的缺点。在空间相关性提取中,本文所采用CNN能从序列中稳定地捕获空间相关特征。此外,本文将时空注意力引入PM2.5预测建模,进一步提升了模型对时空特征的提取能力。

1 相关研究综述

1.1 PM2.5浓度细粒度预测模型研究

1.1.1 线性统计模型与时序模型

线性统计模型和时序模型是根据观测数据,通过曲线拟合和参数估计建立数学模型。Donnelly等[11]针对颗粒物浓度预测提出了几种线性统计模型。Reisen等[12]采用了季节性自回归分数整合移动平均模型(seasonal autoregressive fractionally integrated moving-average,SARFIMA)结合广义自回归条件异方差模型(generalized auto regressive conditional heteroskedasticity, GARCH)的时间序列分析预测方法,他们认为颗粒物的日平均浓度可能是一个具有时变方差(波动性)的季节性积分过程。然而,PM2.5扩散演化是一个动态的非线性过程,线性统计模型和时序模型难以反映其复杂性,预测偏差普遍较大。

1.1.2 浅层神经网络

由于浅层神经网络如支持向量回归(support vector regression,SVR)、人工神经网络(artificial neural network,ANN)等具有良好的性能,目前许多研究都将这类模型应用于预测任务。相比线性统计模型与时间序列模型,浅层神经网络对于原非线性系统的表现性更强、预测表现更佳[13]。王馨陆等[13]使用ANN进行了PM2.5预测研究,该模型能很好地学习输入和输出之间复杂的非线性依赖关系,且具有较好的鲁棒性和自适应特征,提升了预测精度且具有较低的时间复杂度。Stafoggia等[14]和Wei等[15]基于随机森林模型对PM2.5预测进行了研究,该模型预测精度较高,但时空开销大使得模型的运行效率较低。Sun等[16]和Liu等[17]使用支持向量机回归模型来进行PM2.5浓度预测,在小规模的数据集上取得了理想的预测结果。浅层神经网络的局限性是在有限样本和计算单元的情况下对复杂函数的表示能力有限,使模型的泛化能力受到一定的制约。

1.1.3 基于深度学习建模

深度学习模型近年来在空气污染物预测方面得到了广泛的关注与应用,深度学习可以在高维数据中发现潜在的复杂非线性结构[18]。目前应用于空气污染物浓度预测的深度学习模型大致可以分为三大类:基于序列的模型、基于图的模型和基于卷积的模型。

基于序列的模型可以提取长期时间依赖关系,主要包括RNN、长短时记忆网络(long-short term memory, LSTM)、门控循环单元(gate recurrent unit,GRU)等。Hopfield[19]提出的RNN可以通过共享参数和传递隐式状态来对时间序列数据建模,提取上下文的时间依赖性。随后,RNN变量模型LSTM[20]和GRU[21]一定程度上解决了RNN梯度消失带来的短期记忆问题。Zhang等[22]采用ConvLSTM模型对天级测站数据、日均气溶胶光学厚度数据建模,以预测PM2.5浓度的按天空间分布。然而,这些基于RNN的序列方法仍然存在迭代传播时间、梯度爆炸、梯度消失[19-21]等问题。

基于图的模型可有效提取PM2.5的空间分布特征并提升模型预测精度。GCN能够很好地对图数据的结构属性和节点特征信息进行建模,有效地提取监测站之间的空间相关性特征[7]。Wang等[23]利用GCN建模提取PM2.5的时空依赖性,采用图卷积层从多节点构成的时空图中提取空间特征,并利用注意力机制提升了模型对空间特征的提取能力,模型取得了较好的预测表现。虽然图模型在一定程度上提高了PM2.5的预测精度,但图模型仍存在一定的局限性。例如,模型训练的复杂性和运行时间、人为定义变量之间的关系、利用马尔可夫假设解释变量间的交互[6]。在实验中发现,由于各种外部影响,基于图的方法很难捕捉动态时间序列之间稳定的连接关系。

基于卷积的模型也逐渐在PM2.5时空预测建模领域兴起,主要包括因果卷积网络(causal convolution network, CCN)与CNN。CCN最初是为计算机科学中的音频生成和自然语言建模而设计的,可以提取时间序列中长时间相关的特征[24]。CCN架构中的卷积是因果关系,对给定时刻的预测仅依赖于历史数据,避免了过去信息的泄漏。此外,CCN的体系结构不包含复杂的递归结构,因此CCN相比RNN模型训练内存占用更少且不易产生梯度问题[25]。此外,CNN可以通过卷积核捕获局部感受野的空间信息,通过多层卷积和池化层获得全局空间特征,该模型具有并行计算和梯度稳定的优势,且相比GCN能更稳定地提取空间特征[6-7]。Zhao等[26]融合CNN和CCN网络构建了细粒度PM2.5预测模型ST-CCN,实现了PM2.5浓度的细粒度、精确化预测。但该研究对于模型参数的选择采用网格搜索方法,很大可能会陷入局部最优超参数的问题,难以逼近模型最佳性能。因此,本文对ST-CCN采用基于贝叶斯的优化调参方法进行改进。

1.1.4 专业模型

专业模型主要依据污染物形成与扩散的专业背景知识,将大气物理和化学过程的先验知识用作空气污染物浓度预测的基础理论[27-28]。Zheng等[29]构建了面向源的化学扩散模型(chemical transport models,CTMs),此方法通过排放清单、气象与化学机制估计空气污染物浓度。这种确定性方法的优点是具有坚实的理论基础和相对透明的模型。然而,确定性专业模型严重依赖理论假设,对实际物理过程存在描述不足、难以解释等问题,造成较大预测偏差。

1.2 影响因素选择

1.2.1 时空影响因素

根据地理学第一定律,任何事物都是与其他事物相关的,只不过相近的事物关联更紧密[30]。临近测站空气污染物浓度与目标测站空气污染物浓度之间存在天然的空间相关性。从大量时间序列建模经验来看,选定测站空气污染物浓度的历史时间序列之间也存在高度的时间相关性,因此将空气污染物排放与扩散过程中蕴含的时空相关性作为本文建模的基础与出发点。

时空相关性在空气污染预测中得到广泛关注[31-32],研究人员提取空间因素进行预测,赵彦明[33]以目标站点为中心,选取距离最近的5个站点数据作为空间信息输入。Bai等[34]通过对不同空间窗口里的周边站点与目标站点的相关性进行敏感性分析,确定平均相关系数最大的距离作为最佳空间范围。Pak等[35]通过提取不同位置多个监测站的时间序列的时空相关性来进行预测,取得了更准确、更稳定的预测性能。上述研究利用自定义的方法选择周边强相关站点作为空间相关性信息缺乏科学性,且无法高效提取监测站点数据中的时空依赖性。

1.2.2 其他影响因素

在细粒度PM2.5浓度建模中,其他影响因素与PM2.5的相互作用不可忽视。郭利等[36]指出PM2.5与空气污染物、气象因素之间存在较强的相关性,Chen等[37]认为PM2.5与空气其他成分之间也存在交叉影响关系。例如风速、湿度等因素会对PM2.5在空间中的扩散产生影响,低气压则会使PM2.5在空气中飘浮聚集[36],空气污染物成分与PM2.5发生的物化反应也会影响其浓度[37]。此外,交通因素、人类活动、街景建筑、城市地形等对PM2.5的产生、扩散、演化都会产生不同程度的影响。

本文综合考虑PM2.5浓度的时空相关性以及空气污染物、气象因素与PM2.5之间相互作用关系,以反映复杂、动态、非线性的PM2.5浓度变化过程。

1.3 认知计算

认知计算是一种类心智计算(mind-like computation)。认知计算模仿人脑认知过程,开发一种连贯的、统一的、普遍的机制,不是将零碎的解决方案组装起来,通过各自独立的解决方案构建不同的认知过程,而是寻求实现一个统一的计算理论,被认为是计算的第三时代(the third era of computing[10,38])。认知计算能够在没有持续人工监督的情况下解决复杂的问题[39],另一个重要作用是其解释和生成新信息的能力[40],解决当前基于大数据的AI系统普适性的问题,是未来通用人工智能的重要研究方向[8],当前已在医疗保健、网络安全、大数据和物联网等领域得到了广泛的应用[39],为细粒度空气质量预测提供了一条可以借鉴的思路。

2 时空认知膨胀卷积网络

2.1 本文研究总体框架

本文基于认知计算理论[39-40],认为多源异构数据(如空气污染数据、气象数据等)能够感知更多信息[40,41-42], 更能反映实际环境中PM2.5的时空扩散聚集过程,另外时间与空间2个维度数据的融入能够体现人脑的层级认知结构,从而形成一种连贯、统一、普遍的建模机制。实际研究内容包括数据预处理、基于时空注意力的ST-C-DCN、基于贝叶斯优化器的参数调优以及模型检验。本文研究的框架如图1所示。

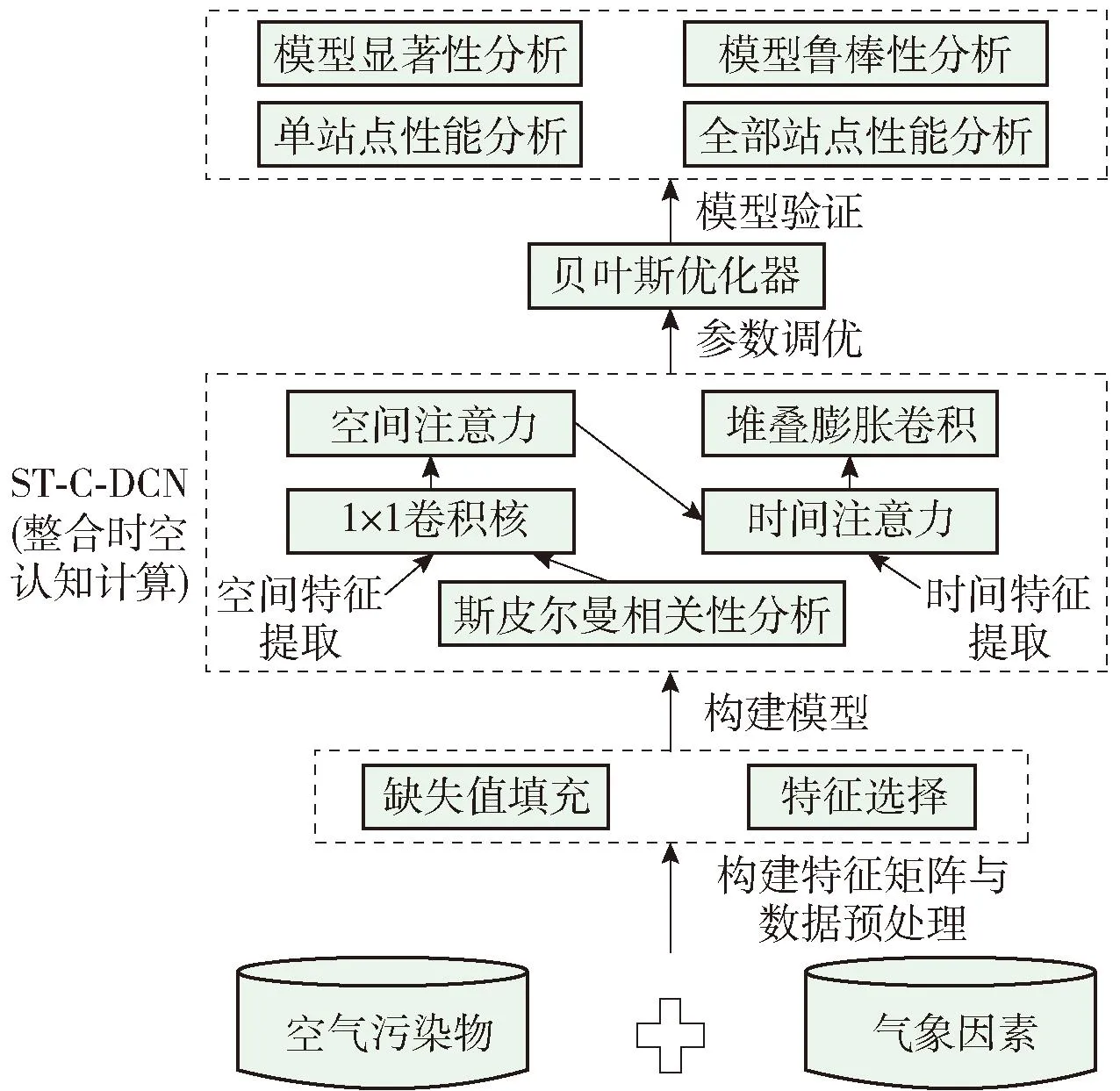
图1 研究框架Fig.1 Research framework

本文将多种空气污染物和气象因素纳入PM2.5预测建模,挖掘序列间的时空依赖关系以提升PM2.5预测精度。本文研究思路包括:首先,对获取到的空气污染物和气象因素进行数据预处理,经过缺失值填充和特征选择将多测站数据融合重构为三维特征矩阵,并作为模型输入。其次,所构建的ST-C-DCN主要包括空间特征提取和时间特征提取2个部分。在空间特征提取模块中,本文使用斯皮尔曼相关性分析获取与目标站点强相关的站点,然后将强相关站点数据重构为三维矩阵,通过1×1卷积核和空间注意力模块对三维矩阵进行升维、降维处理,以优化模型对空间相关性特征的提取能力。空间注意力模块处理后的特征矩阵,端到端地作为时间特征提取模块的输入。在时间特征提取模块,利用时间注意力机制从特征矩阵中筛选自依赖性强的时域(时间间隔)作为堆叠膨胀卷积的数据窗口,并将特征矩阵作为堆叠膨胀卷积的数据输入。通过堆叠膨胀卷积,提取有效的时间依赖特征对未来一个时刻的PM2.5值做出预测。然后,采用贝叶斯优化器自动调优模型超参数。最后,不仅将ST-C-DCN与一系列基线模型进行了单测站性能分析。而且基于全部测站性能分析、模型间差异的显著性检验、模型鲁棒性分析验证了模型的泛化性、准确性和鲁棒性。

2.2 基于空间注意力的空间信息提取

本文综合考虑PM2.5浓度的时空相关性以及空气污染物、气象因素与PM2.5之间相互作用关系,以反映复杂、动态、非线性的PM2.5浓度变化过程。

本文利用斯皮尔曼秩相关系数来度量周围其他站点与目标站点时间序列的相关程度,计算得到的相关系数介于0到1之间。相关系数越趋近于1代表2个站点的相关性越强。计算式为

(1)

式中:ρ(Y,Yk)为2个序列的斯皮尔曼相关性系数;Y为目标站点的PM2.5历史数据按数值降序排序后的序列;Yk为周围某站点的PM2.5历史数据按数值降序排序后的序列;N为序列中样本数量。

ρ_list为计算出的目标站点与所有站点(S)之间的相关系数,即

ρlist=[ρ(Y*,Y1),ρ(Y*,Y2),…,ρ(Y*,YS)]

(2)

本文认为站点间相关性系数超过0.85即可说明二者存在强相关性,因此将相关性阈值ρth设置为0.85[35],最终得到与目标站点强相关的M个站点,并将M个站点的特征矩阵聚合为

X={xi|ρ_list>ρth,i∈1,2,…,M}

(3)

其中将目标站点与第i个站点的相关性系数ρ(Y*,Yi)与阈值ρth进行了比较,若大于阈值则将第i个站点视为强相关站点。Xi∈RT×L作为编号为i的站点数据,与其他强相关站点数据融合构成数据集X[26],式中:X∈RM×T×L为与目标站点空间强相关的三维特征矩阵,其中M≤S,M为与目标站点空间强相关的站点数量,T为历史数据时间步长,L为特征维度。利用1×1卷积核实现特征矩阵升维,经过升维处理后三维矩阵变为X∈RMnew×T×L,其中Mnew为升维后的通道数量。

如图2所示,利用CNN中的1×1卷积核以增加输出通道数的方式对特征矩阵A进行升维处理[35]。中间的矩形框中包含了Mnew个滤波器,滤波器的维度是1×1×k(k为卷积核数),其中卷积核数与原有特征矩阵的通道数相同。在局部视角,3个红色方形块与Mnew个滤波器经过卷积计算,得到Mnew个黄色方形块。Mnew的值与卷积层的滤波器数量一致,滤波器数量决定输出结果的特征图个数,本文通过对滤波器数量等超参数进行对比调优,设定第一个卷积层中的滤波器数量Mnew值为64。从全局角度,升维处理对原始特征矩阵的通道数进行了扩充,新生成的特征矩阵为X∈RMnew×T×L。在升维过程中,特征矩阵与滤波器的卷积运算使不同通道信息得以交互和融合,提升了模型对非线性特征的提取能力。

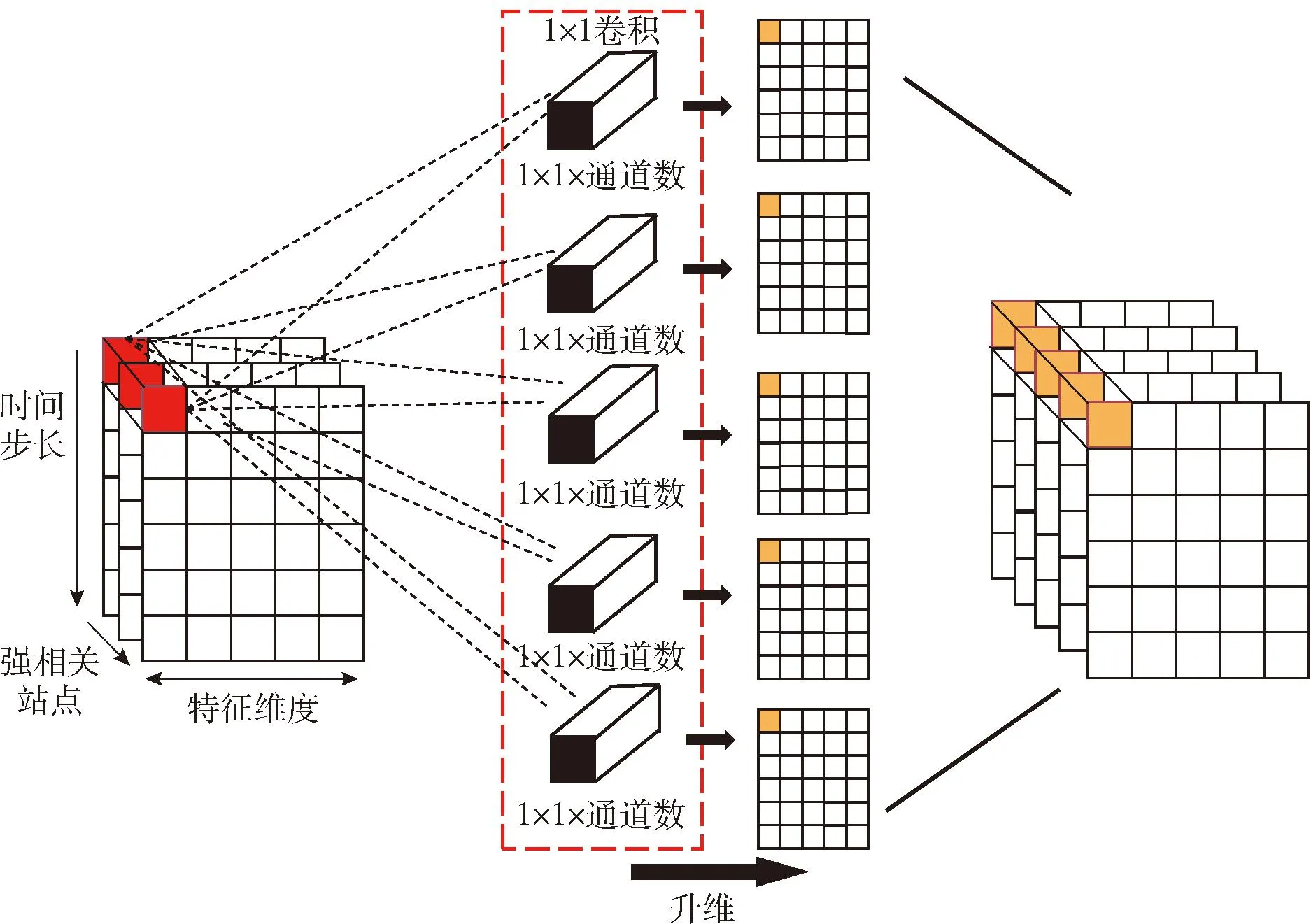
图2 利用1×1卷积核对特征矩阵升维处理Fig.2 Dimension raising of the eigen matrix via 1×1 convolution kernel

基于空间注意力机制的特征矩阵降维过程如图3 所示。

图3 利用空间注意力模块对特征矩阵降维Fig.3 Dimension reduction of eigen matrix via spatial attention

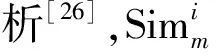
(4)

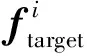
(5)

最后,将各通道的第i项特征序列乘以对应的权重值再求和,使第i项特征序列聚合为最终序列,由聚合后的各项特征序列构成最终特征矩阵[26]。因此最终降维聚合后的特征序列Ai及特征矩阵A的计算式为

(6)

2.3 融合时间注意力的膨胀卷积网络

本文根据时间注意力机制,利用贝叶斯优化方法,以模型预测精度为评价指标,筛选依赖性强的时间间隔作为膨胀卷积的输入窗口尺寸,以优化膨胀卷积对时间依赖特征的提取。首先,本文设定滑动窗口尺寸范围为[4,24],并以4为间隔进行采样。其次,利用MSE、RMSE、MAE、R2等指标,选择使模型预测性能最佳的滑动窗口。经过调优,膨胀卷积的滑动窗口被设置为24。

然后,本文将聚合后空间特征矩阵作为膨胀卷积输入,利用堆叠膨胀卷积模型提取二维特征矩阵中时间依赖特征。堆叠膨胀卷积架构如图4所示。

图4 堆叠膨胀卷积的架构Fig.4 Architecture of stacked dilated convolution

图4中堆叠膨胀卷积以特征映射的方式与前一层的局部感受野连接。首先使用共享卷积核做运算,再利用激活函数的非线性计算得到特征值。如图4所示,输入层中3条数据为1组,经过膨胀卷积运算映射为隐藏层中的一个特征值。膨胀卷积与普通卷积的卷积核大小和卷积操作是一样的,即参数的数量不变。区别在于膨胀卷积引入了膨胀率,该参数使得卷积核处理数据时可以跳过d个数据进行处理,即间隔采样。如图4,在输入层中,卷积核以间隔为1进行采样;在第1个隐藏层中,卷积核以间隔为2进行采样;在第2个隐藏层中,卷积核以间隔为4进行采样。膨胀卷积这种独特的结构使它无须很大网络深度就可以获得较大的感受野,并获得长距离的历史数据。不仅降低了空间损失和信息损失,且使得特征提取更全面,有利于提升模型整体的预测精度。膨胀卷积式为

(7)

式中:fk(k=1,2,…)表示滤波器;xi(t=1,2,…)代表输入的特征序列;d为膨胀率,表示模型采样的节点间隔;K为卷积内核大小,表示局部感受野中参与膨胀卷积运算的节点数。堆叠膨胀卷积的感受野大小为(K-1)d+1,通过增大卷积内核或膨胀率可以使模型获得宽阔的感受野。根据Zhao等[26]的研究,本文将卷积内核数设置为3,网络层深度置为4,堆叠膨胀卷积率设置为d=2i,其中i为网络层深度。在后续实验中本文将利用贝叶斯调优方法对堆叠膨胀卷积模型的其他参数进行进一步优化。

3 实验

3.1 研究数据与研究区域

本文选取中国海南省的海口市作为研究区域。根据城市监管和建设要求,海口市空气监测站分布在秀英区、龙华区、琼山区、美兰区4个区的北部。海口市空气监测站点分布如图5所示。

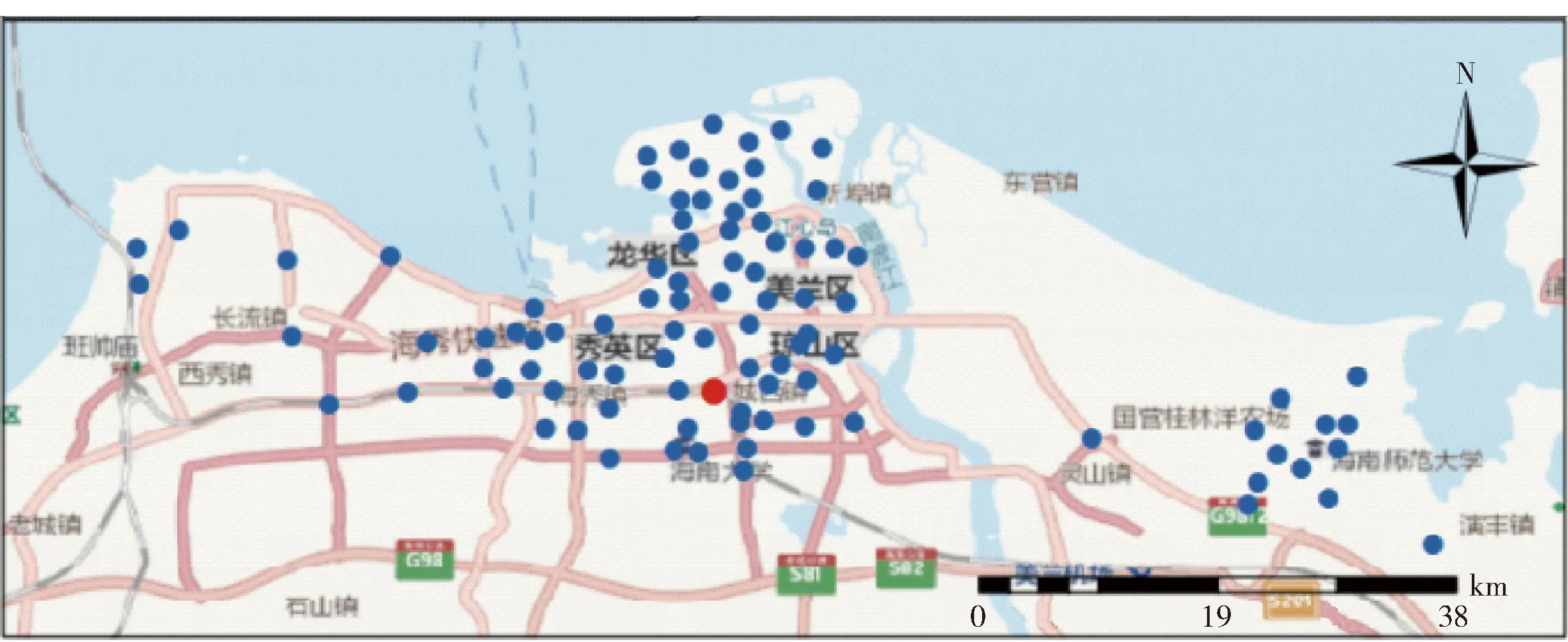
图5 海口市空气监测站点分布Fig.5 Distribution of air monitoring stations in Haikou

本文从站点分布密集的中部区域随机选择一个站点(图中红色圆点位置的站点),将其作为本文实验的目标站点。对该站点的PM2.5进行预测,能够较好地反映时空相关性对模型预测的影响,具有一定的代表性。

本文收集了海口市95个空气监测站于2021年3月1日至2021年4月20日的空气污染物、气候因素小时级数据,并构建了原始数据集。本文对原始数据进行了数据预处理,包括缺失值处理和特征选择。对于短时间跨度(1 h或2 h)的缺失值采用一阶、二阶拉格朗日插值法进行填充,对于长时间跨度(5 h及5 h以上)的缺失值,使用临近日期的同时段数据插补。其次,采用斯皮尔曼秩相关性系数方法识别并剔除原始数据集中与PM2.5弱相关的特征。最终选择的特征包括PM2.5、PM10、NO2、CO、O3、SO2、温度、气压、相对湿度、风向、风速共11项特征,11项特征序列构成每个站点的原始数据集。各项特征的详细描述,如表1所示。

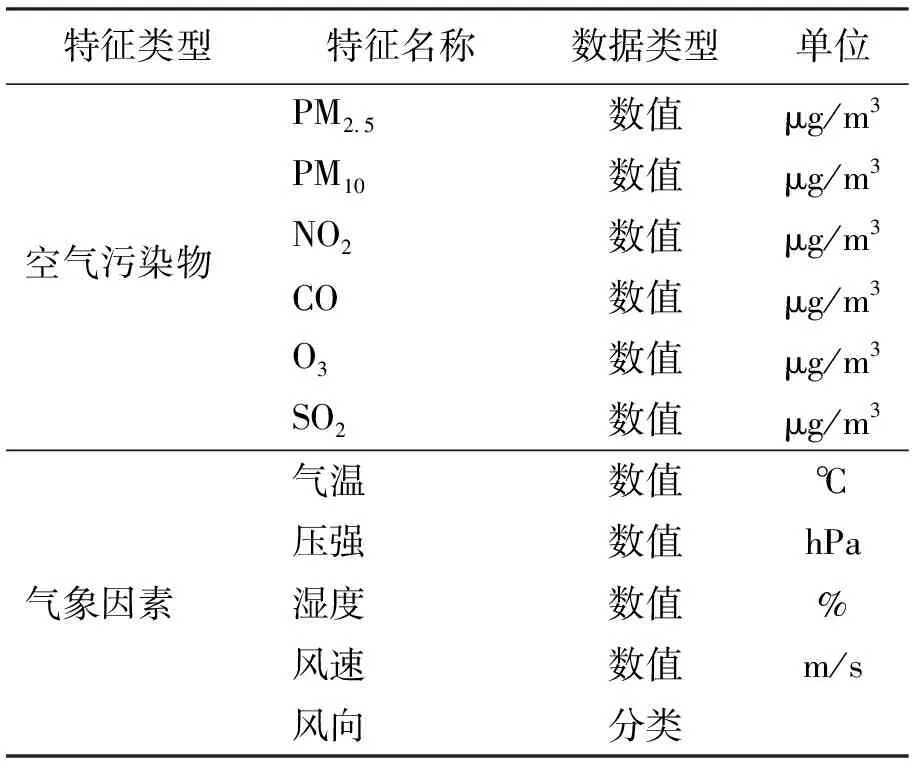
表1 研究数据属性列表

3.2 基于贝叶斯优化的超参数调优

ST-C-DCN模型的性能是由许多超参数决定的,例如网络深度,隐藏层节点数等,需要根据经验或采用随机、网格搜索等方法寻找最优的参数组合。然而经验法或随机搜索需要大量实践的经验,无法精确获取最优超参数。网格搜索不仅会随着参数个数的增加,极大地提高搜索成本,而且针对一些非凸问题易取得局部最优。当前热门的贝叶斯优化调参方法,采用高斯过程考虑之前的参数信息,并不断地更新先验,而且具有调参迭代次数少、速度快等优势[41]。因此本文通过构建贝叶斯优化器对模型进行自动调参,以高效、精确地捕获适合于该模型的最佳参数组合。贝叶斯优化的基本过程如图6所示。

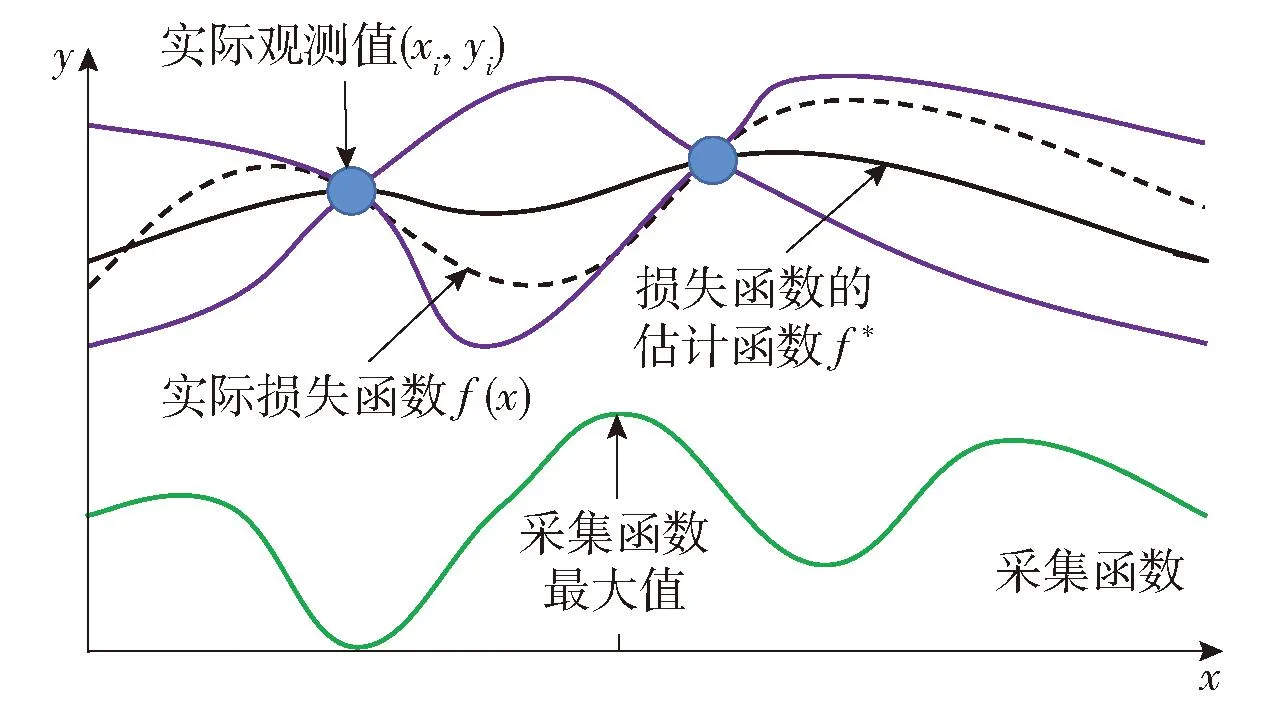
图6 贝叶斯优化的基本过程Fig.6 Hyperparameter tuning process of Bayesian optimization

贝叶斯参数调优的最终目标是选出一组超参数使得模型的损失函数获得全局最小值。对于一个黑盒模型,无法获取它的实际损失函数,只能通过计算近似函数并通过不断迭代去逼近真实损失函数,从而获得使模型损失值最小的超参数组合。图6中横轴表示超参数组合的搜索空间。蓝色的点表示已知的实际观测值,即(xi,yi)。其中,xi代表一组超参数值,yi代表模型训练后得到的损失函数值。黑色实线为估计得到的函数分布,紫色实线之间的区域为估计函数的置信区间。黑色虚线表示实际的模型损失函数,绿色实线表示采集函数。首先,贝叶斯优化器基于观测点,利用高斯混合模型的TPE过程(概率代理函数),得到损失函数f(x)的估计函数f*。其次,优化器利用概率代理模型的输出结果(f*)计算出采集函数,并利用采集函数选择下一个观测点。采集函数会衡量观测点(参数搜索空间中的样本点)对于拟合f*与f(x)的影响程度,并选择影响最大的点来执行下一步的观测。图6中,贝叶斯优化器计算得到了采集函数的最大值点x,然后将x代表的这组超参数带入模型中去训练,得到实际损失值y。最后将新的观测点(x,y)加入已知的观测点中。通过一定的迭代次数,估计函数f*会逐渐逼近实际损失函数f(x),计算f*的最小值点即为调优后的超参数组合。

本文利用贝叶斯优化器调优了堆叠膨胀卷积中的hidden_size、levels、kernel_size、dropout这4项参数。其中hidden_size表示隐藏层中的节点数目,levels表示网络层深度,kernel_size为膨胀卷积内核,dropout为每次迭代随机移除的节点比率。

在贝叶斯优化过程中,本文将模型在验证集上的均方根误差(root mean square error, RMSE)值作为优化器的损失函数。对于目标站点,由图7可知,贝叶斯优化器在38次迭代后趋于收敛。考虑到模型运行时间较长,本文的贝叶斯优化器迭代次数选择50。

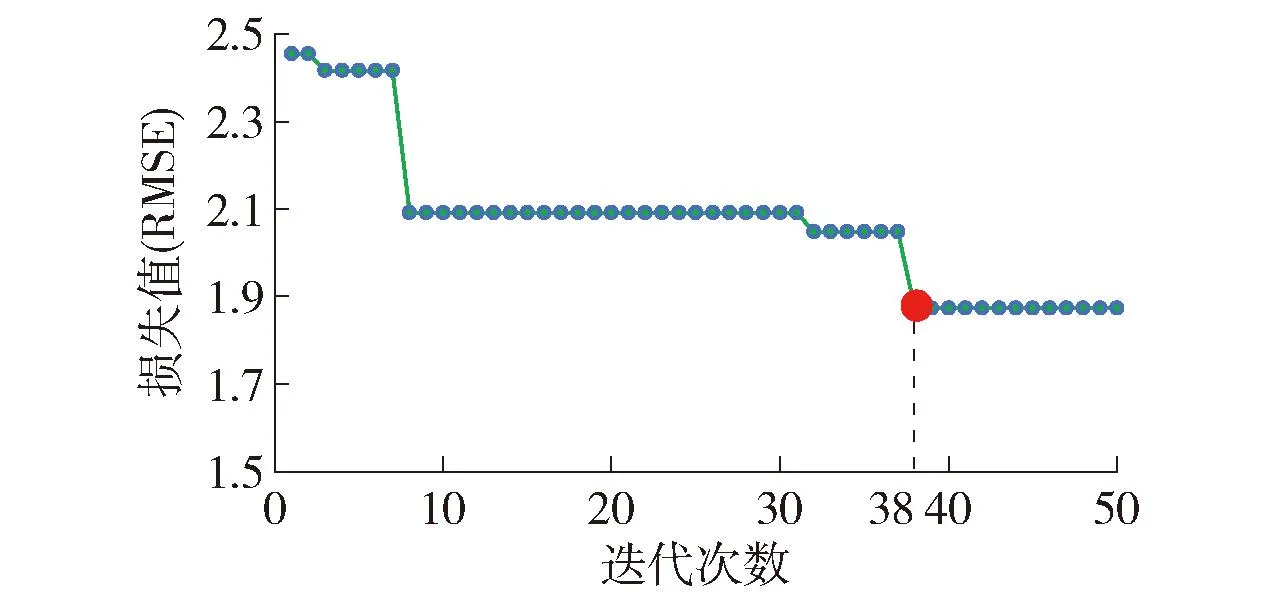
图7 迭代次数对模型损失值的影响Fig.7 Influence of the number of optimizer iterations on the model loss value

超参数优化选取的范围分别设置为:dropout取值范围是0.5～0.9,步长为0.01;kernel_size取值范围是3～9,步长为1;levels取值范围是3～9,步长为1;hidden_size取值范围是48～64,步长为8[26]。图8展示了超参数的贝叶斯优化过程。经过50次迭代,模型的最佳参数组合为:dropout为0.59,hidden_size为56.0,kernel_size为9.0,levels为3.0。经过反复实践,优化后的参数组合在不同站点数据集上都取得了良好的预测结果,这组参数也被运用于下文实验中。

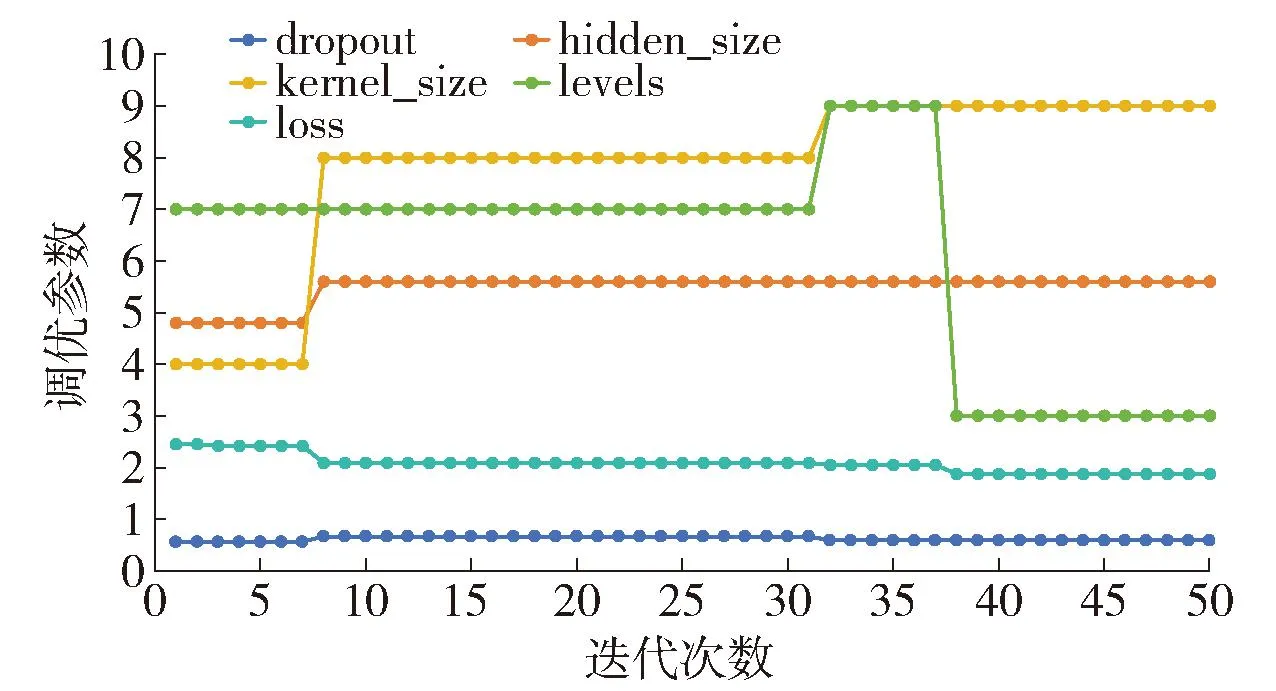
图8 优化器迭代过程中的超参数值变化Fig.8 Bayesian optimization process of hyperparameters

3.3 模型性能分析

3.3.1 单监测站性能分析

在本文中,随机选取一个站点作为目标站点(图5中的红色圆点),并基于调优后的超参数利用ST-C-DCN模型对目标站点的PM2.5进行了预测。

为了检验模型对PM2.5浓度的细粒度预测效果,本文选择以下模型作为基准。基准模型包括基于时间序列的自动回归模型(autoregression,AR)、移动平均模型(moving average,MA)和自回归移动平均模型(auto regressive moving average,ARMA)模型,基于浅层神经网络的SVR和ANN模型,以及基于深度学习的常用序列建模方法,包括GRU和LSTM和基于图的时空图卷积网络(spatial temporal graph convolution network,STGCN)。时空因果卷积网络(concentration prediction via spatial-temporal causal convolution network,STCCN)模型相关参数参考文献[26]。由于ST-C-DCN的输入结构和建模原理与专业模型差异较大,因此本文不考虑CTMs等专业模型。

基准模型的参数设置如下:AR模型的系统阶数p设置为3。采用最小二乘法估计MA模型的自相关系数,设置MA模型的阶数为3。通过求实验样本的自相关系数和偏自相关性系数,将ARMA模型的p、q阶数分别设置为5、6。在SVR模型预测PM2.5浓度的测试中,目标函数的惩罚系数设置为1,内核参数采用径向基函数[17]。ANN模型设置包含2个隐藏层,每个隐藏层各包含50个神经元,使用ReLU激活函数与Adam随机梯度优化器等模型参数[13]。LSTM与GRU模型的单元隐藏层的尺寸为7,权重初始化方法采用均匀初始化器,并在后面增加全连接层对输出进行维度变换[22]。ST-GCN区块3层通道分别设置为64、16和64。并将图卷积核大小K和时间卷积核大小Kt设置为3[7]。ST-CCN模型的归一化方法、数据分割比、dropout、kernel_size、hidden_size等超参数均参考文献[26]进行设置。

对于线性统计与时序模型,本文将PM2.5历史序列作为模型的输入。对于浅层神经网络和深度学习模型,采用和ST-C-DCN相同的特征序列作为输入。此外,利用文献中的一般性参数配置对上述基准模型的参数进行多次测试,选取基准模型预测性能最好的参数。

为简单起见,选择22时的PM2.5浓度作为目标输出,22时前24 h的PM2.5浓度作为输入。由于海口是典型的热带城市,夜晚22时后,烧烤、娱乐等人为活动的增多,导致此时PM2.5浓度的方差波动相对较高。

本文采用均方误差(mean square error,MSE)、RMSE、平均绝对误差(mean absolute error, MAE)、拟合优度(R-squared,R2)作为各种模型的评价指标,并使用5折交叉验证方法获得各模型性能。将5次交叉验证所得的平均MSE、RMSE、MAE和R2作为各模型的最终性能,各模型最优预测结果如表2所示。

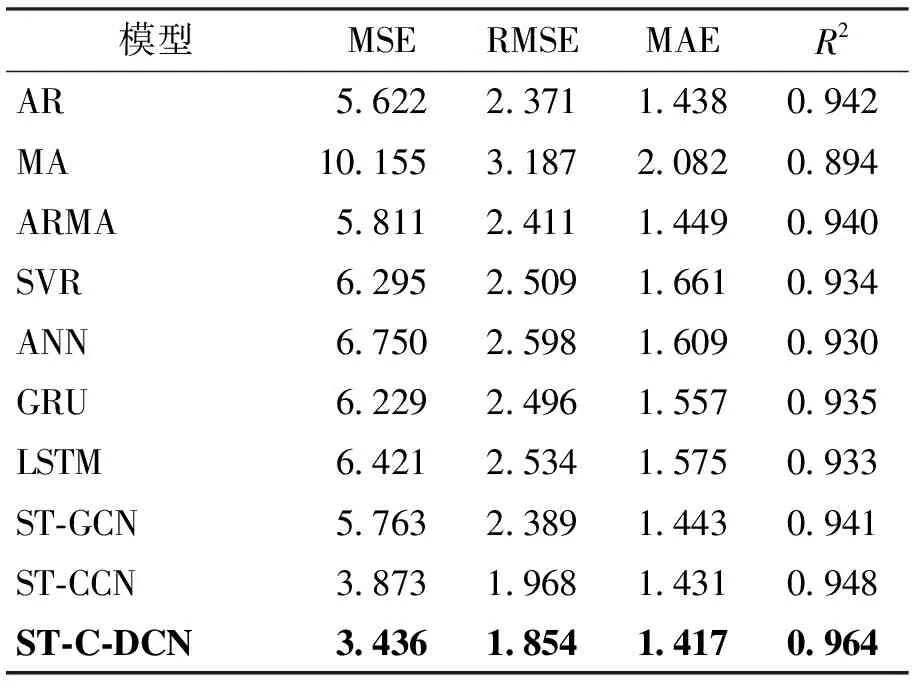
表2 基准模型和ST-C-DCN预测性能汇总表

如表2所示,ST-C-DCN模型相比基准模型,它的MSE、RMSE、MAE分别平均下降了42.61%、24.7%、9.93%,R2平均提升了3.35%。实验结果对比,证明了模型在PM2.5细粒度预测的潜力。为了方便直观对比各模型,本文绘制了各模型性能条形图,如图9所示。

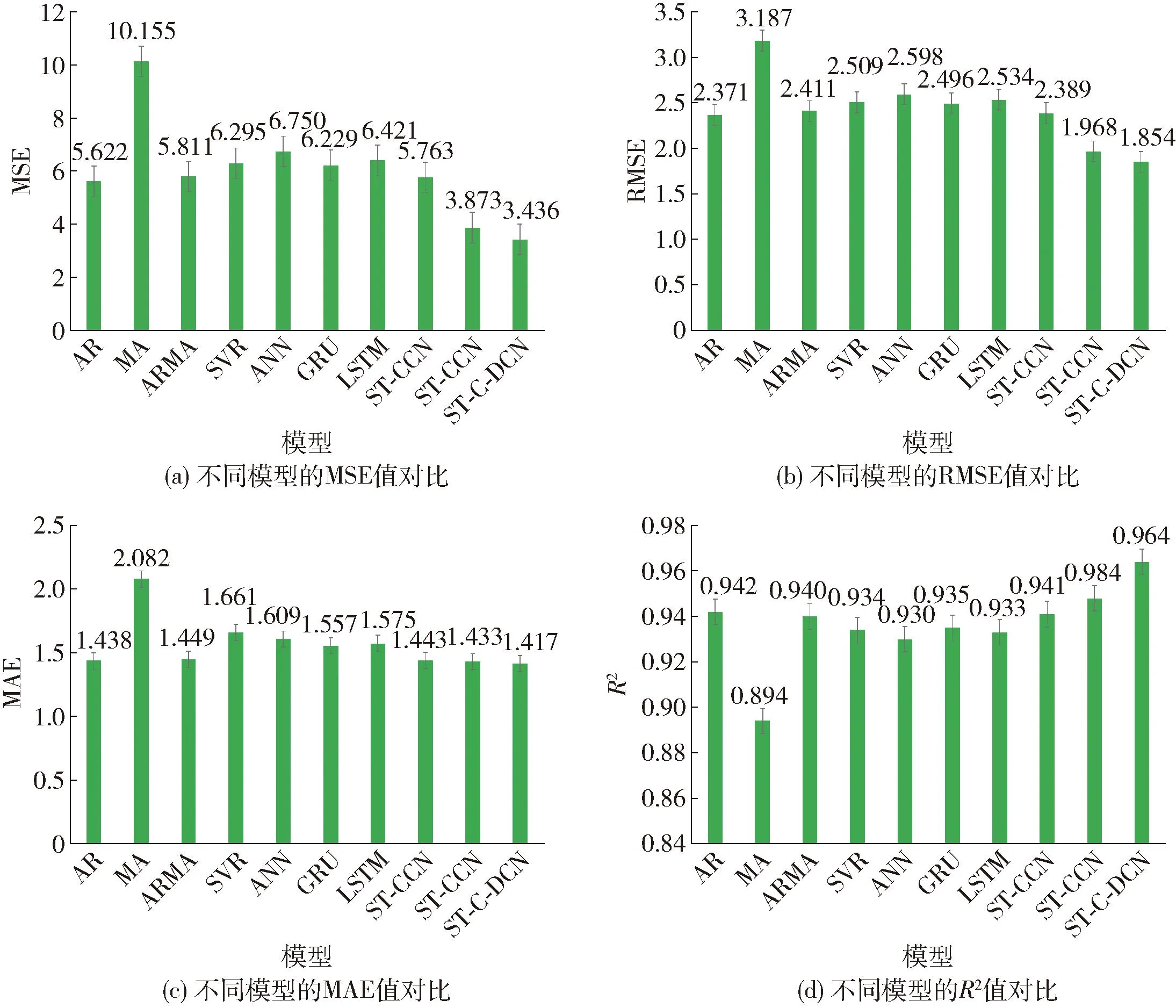
图9 模型性能对比Fig.9 Performance comparison between baselines and ST-C-DCN

在图9中,从整体上看,深度学习模型的预测性能优于浅层神经网络。这是因为深度学习模型可以在高维数据中发现潜在的复杂非线性结构,且对于动态非线性系统的表现能力更强。出乎意料的是,传统的AR模型的预测结果(包括MSE、RMSE、MAE、R2)均优于浅层神经网络及深度学习模型。对这种现象的一个可能的解释是,由于实验数据的强周期性,基于线性和时间序列的模型可以更好地提取时间依赖性。

3.3.2 全部监测站性能分析

为了进一步证明模型对PM2.5预测的稳定性与泛化能力,本文利用ST-C-DCN与基准模型对95个站点的PM2.5浓度进行了单步预测。以MSE、RMSE、MAE、R2作为模型评价指标,并使用5折交叉验证方法获取模型对每个站点的趋于真实的预测性能。如表3所示,本文总结了10种模型的win-tie-loss实验结果。

表3 win-tie-loss实验结果汇总表

从表3可以看出,所提出的ST-C-DCN在大多数站点的预测中,4项评价指标优于其他基线。ST-C-DCN在RMSE (MSE)、MAE和R2中获胜次数分别是68、63和64。ST-C-DCN在4项指标的对比中获胜次数远远超过ST-CCN、ST-GCN等模型。win-tie-loss实验结果证明本文提出模型具有较强预测稳定性和泛化能力。

接着,本文进一步探讨了ST-C-DCN模型性能的空间分布。全部测站的模型预测性能热力图如图10所示。

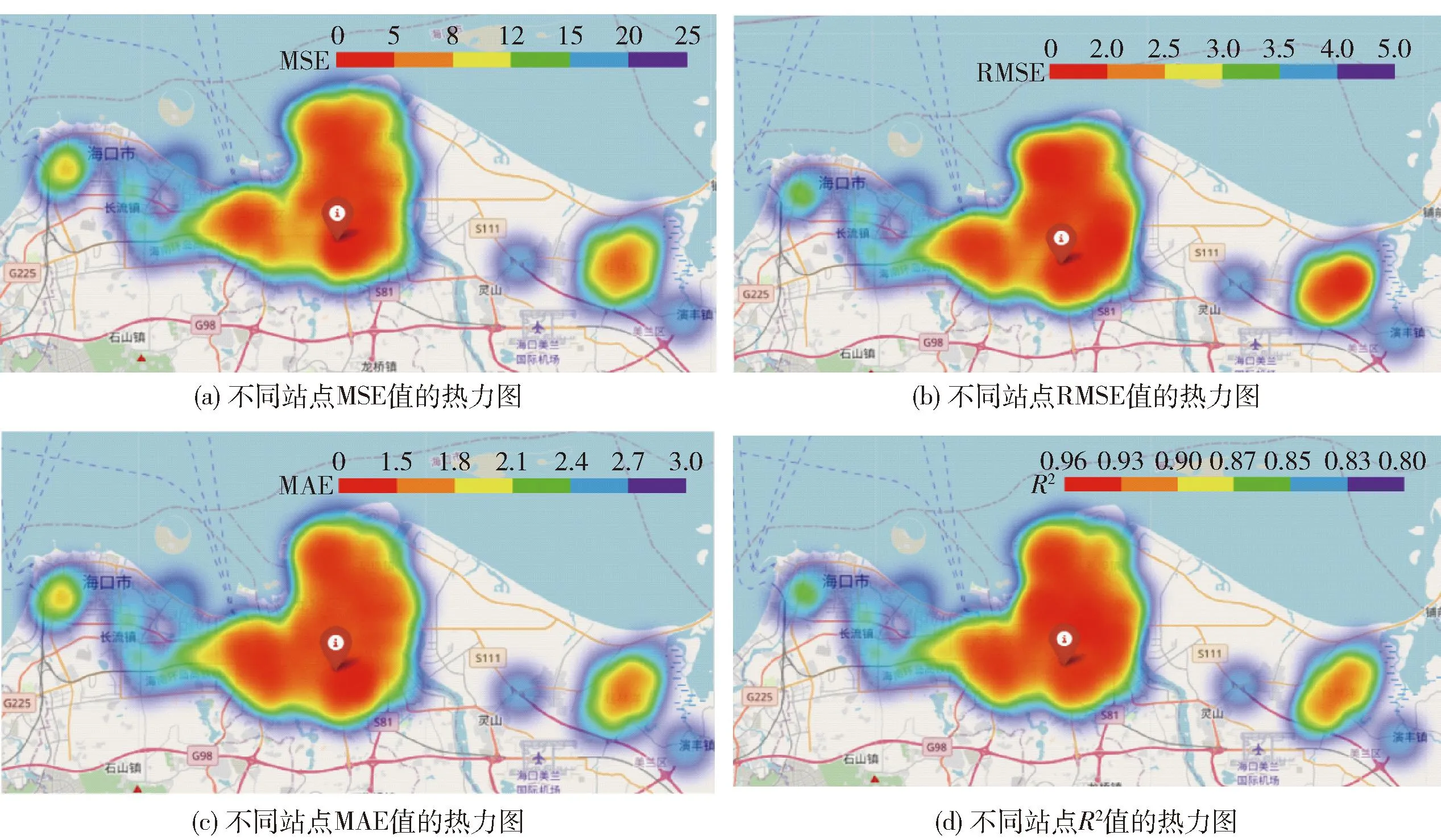
图10 全部95个监测站的ST-C-DCN预测表现Fig.10 Prediction performance of ST-C-DCN for all 95 stations

如图10(a)～(d),可以看到模型对绝大部分站点的PM2.5预测具有较高的精度。ST-C-DCN对处于中部地区的监测站点进行预测时,它的MSE值处于0～8的范围内,R2值保持在0.90～0.96的范围,整体预测表现非常优秀。对95个站点的模型性能取均值后,ST-C-DCN的MSE、RMSE、MAE值分别为4.94、2.17、1.31,R2值为0.92,证明了模型具有较强的预测稳定性和泛化能力。

在绝大多数情况下,ST-C-DCN在边缘站点或孤立站点相比处于密集分布区的站点预测表现更差。这一结果反映出,在细粒度PM2.5建模预测时,不应该忽视空间分布信息的影响。然而,模型对某些处于密集分布区的站点进行PM2.5预测时也表现出较大的预测误差。可能的原因是该站点处于人口密度大的市区中心,复杂的外部影响因素对PM2.5质量浓度预测有较大的负面影响,这应该在未来的PM2.5预测建模中加以考虑。

3.4 模型鲁棒性、泛化性分析

3.4.1 显著性检验

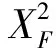
(8)

表4 10种模型在3种数据集上RMSE指标排名

式中:N和k分别表示独立数据集数与模型数量;Rj表示第j个模型在不同数据集上的性能指标平均排名。

(9)

分别计算出了10种模型在3个数据集上的RMSE值的平均排序数,如表4所示。

3.4.2 模型鲁棒性分析

本文的ST-C-DCN模型采用随机种子来确保模型每一次初始化的参数一致,从而达到模型预测结果一致的目的。本文为了测试模型预测的稳定性,通过随机选择随机种子来变换模型的初始参数,使模型有不同的预测结果。利用模型对全部站点未来24个时刻分别进行预测,并对每个时刻进行了10次测试,最终实验结果为三维矩阵X∈RS×H×T,其中S表示监测站点数,H代表不同时刻,T表示测试次数,从S轴将聚合实验结果,将实验结果压缩至二维,即Xnew∈RH×T。本文基于降维后的数据绘制成小提琴图,如图11所示。

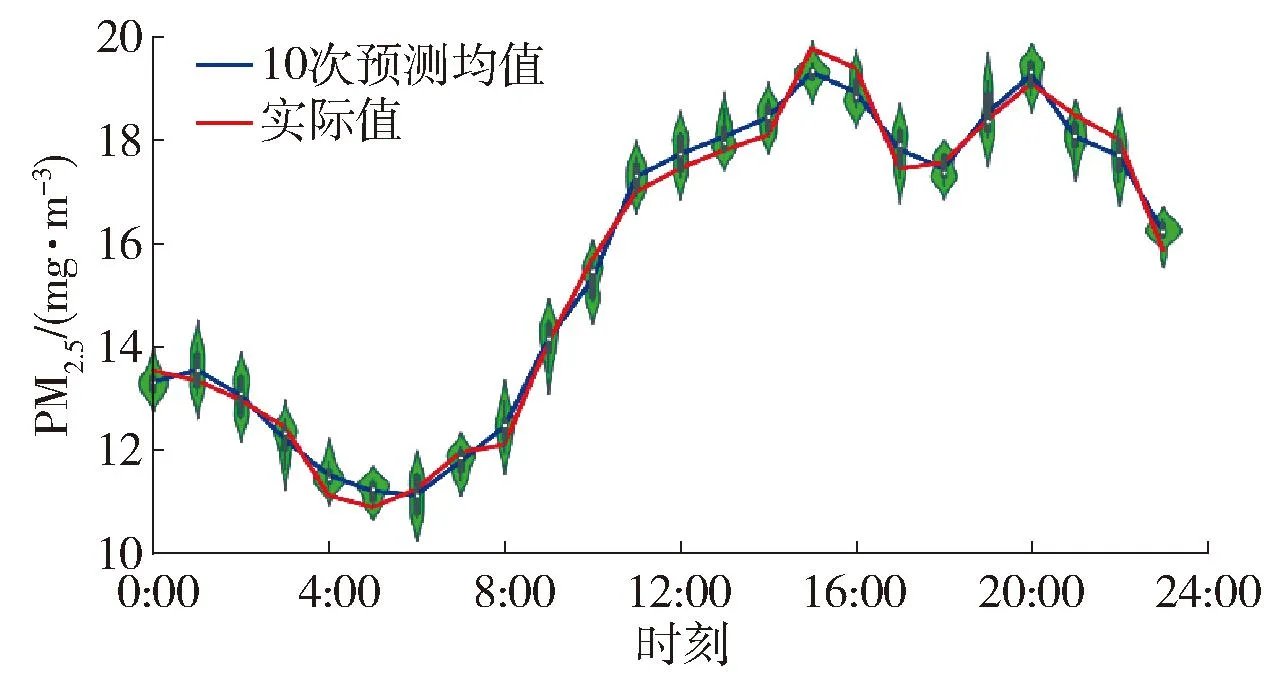
图11 各时刻模型预测性能小提琴图Fig.11 Violin figure of PM2.5 prediction at 24 moments

图11中,横轴表示未来一天的24个时刻,纵轴表示PM2.5的预测值。不同时刻对应的小提琴子图中有5种不同的统计量,其中线段的上下边界分别表示外限和内限,黑色矩形的上下边界表示上四分位和下四分位数,中间的空心表示中位数。可以看到不同时刻的10次预测均值与真实值非常拟合,说明模型预测精度较高。此外,在大部分时刻模型预测值围绕真实值在小范围内波动,证明了模型具有不错的鲁棒性。

从PM2.5预测值的走势来看,0:00—6:00由于人类活动大大减少,空气中飘浮的PM2.5得以四处扩散、输送。7:00—16:00由于人类活动增多,交通尾气、工厂生产、燃煤排放等因素使PM2.5浓度迅速上升。16:00—23:00部分工厂已经停工因此PM2.5质量浓度开始下降,但PM2.5预测值仍维持在较高的水平。可能的原因是夜间烧烤、大排档等人为因素使空气中的PM2.5继续积累聚集。为了保护人类赖以生存的空气环境,本文倡导人类低碳出行,并且应尽量减少夜间活动以避免长时间处于高浓度PM2.5环境中。此外,政府部门也应加强空气污染源的管控与整治,减少重度污染天气的产生。

4 讨论

本文将认知计算相关理论引入PM2.5细粒度预测建模,具体包括影响因子选择、模型层次架构以及统一认知机制3个方面,提出的ST-C-DCN模型效果在研究区域的实际空气质量监测方面收到了良好的反馈。本文认为认知计算对于PM2.5细粒度预测具有以下意义。

首先,在模型的影响因子选择方面,认知计算认为多源、多尺度的认知信息更能够模拟、反映人脑对于空气污染的感知过程,因此在模型影响因子选择方面本文不但考虑了多源空气污染物(如PM2.5、PM10、NO2等)对于细粒度PM2.5时序预测的影响,同时也考虑气象条件(如风力、温度、湿度等)对于细粒度PM2.5时空聚集扩散过程的影响,分别通过空间注意力机制与时间注意力机制整合各种时空尺度的认知信息,这种建模思路不但适用于当前细粒度PM2.5浓度的时空预测,也适用于多种认知任务(如PM10、NO2浓度预测等)的完成。

其次,在模型层次架构方面,为了实现认知计算中的层级认知结构,达到用多个层级去表征潜在特征的目的,本文采用堆叠膨胀卷积进行不同时空分辨率下时空分布特征的捕捉,并通过模型性能分析与模型鲁棒性、泛化性分析的具体实验从不同角度验证了本文提出的这种层级认知结构的鲁棒性与稳定性。在实际的计算过程中,本文所采用的堆叠膨胀卷积还表现出良好的计算性能,可以在避免梯度问题的前提下捕获长时、有效的时间特征。

最后,认知计算为细粒度PM2.5浓度预测提供了一个连贯、统一、普适的认知机制,也为细粒度时序预测提供了一条可借鉴的建模思路,解决了当前时序预测领域模型存在的“特定领域、特定场景”的限制,也解决了实际过程中普遍出现的“头痛医头、脚痛医脚”的诟病,适用于开放环境机器学习,认知计算契合当前学术界的最新研究方向,这一领域值得进一步研究与探索。

5 结论

1) 本文考虑了空气污染物间的相互作用,气象因素对PM2.5浓度演化的驱动作用,以及空气监测站点间的时空依赖关系,提出了基于时空认知膨胀卷积网络的PM2.5浓度预测模型(ST-C-DCN)。该模型融合时空注意力机制与膨胀卷积网络,具有梯度稳定和内存需求低的优势,且进一步提升了对PM2.5时空特征的提取能力,提高了预测精度。此外,本文采用了贝叶斯优化器端到端优化模型超参数,高效、精确地将模型参数调到了最优,避免了传统调参方法易得到局部最优参数的弊端。

2) 经过单个站点的预测实验,证明ST-C-DCN在PM2.5浓度预测任务中4项评价指标均优于基线模型,具有较高的精确度。相比基线模型,它的MSE、RMSE、MAE分别平均下降了42.61%、24.7%、9.93%,R2值平均提升了3.35%。并且利用Friedman检验证明了ST-C-DCN的预测性能显著优于基线模型;对于全部监测站点的预测,在ST-C-DCN在win-tie-loss(包括MSE、RMSE、MAE、R2)实验中,获得了最多的获胜次数,分别为68,68、63和64,证明了模型的泛化性较强;对于全部站点未来24个时刻PM2.5的预测实验,显示了模型对于不同时刻PM2.5预测均有着较稳定的预测区间,证明了模型的稳定性和鲁棒性。