具有变泊松运动特性的剪叉式折展机构运动学分析
2024-03-09畅博彦闫圣杰韩芳孝
畅博彦, 闫圣杰, 梁 栋, 关 鑫, 韩芳孝
(1. 天津工业大学 机械工程学院, 天津 300387;2. 天津市现代机电装备技术重点实验室, 天津 300387)
折展机构是一类能够从收拢状态展开至预定结构形式且能承受特定载荷的机构[1-2]。折展机构收拢时具有较小的体积,便于运输和储存,展开时具有较大的包络体积和工作面积。目前,折展机构被广泛应用于土木工程、航空航天和医疗等领域[3-12]。
在工程应用中,泊松比是一个重要的材料参数,其定义为材料横向应变与纵向应变的比值,可用于计算材料的应力状态和变形特性。大多数常见的工程材料具有正泊松比,即其在受压时横向膨胀。相比之下,负泊松比材料在受压时横向收缩,这种材料在抗剪承载力、抗断裂性、能量吸收和压陷阻力等方面比传统材料更具优势。因此,国内外学者针对负泊松比材料提出了多种设计方法。Yang等[13]通过将传统蜂窝网格结构扩展至三维空间的方式,设计了一种可在三维空间内压缩的负泊松比超材料;Babaee等[14]利用屈曲分析方法设计了一种弹性球壳结构,该结构在受到压缩载荷时横向收缩,从而实现三维负泊松比效应;Grima 等[15]通过将正方形胞元的顶点连接成柔性铰链,使正方形能够直接发生相对转动,从而设计得到一种具有负泊松比效应的二维超材料。
折纸技术作为一种设计新结构和超材料的方法,近年来受到了学者们的广泛关注。受折纸启发的结构设计不仅可实现平面与空间之间复杂形状的转换,而且可获得一些在传统材料设计和合成中难以实现的特殊力学性能[16]。此外,折纸结构在面内的折叠变形使其非常适用于拉胀材料的设计,因此各种折纸折痕单元被广泛应用于负泊松比超材料[17]。例如,具有单自由度的三浦折纸图案[18-19]是使用最广泛的折纸图案之一,其已被证明具有大折展率、负泊松比和各向异性刚度[20-22]。Yang 等[23]受折纸启发,提出了一种模块化可重构超材料,将由Sarrus机构和平面四杆机构组成的可转换模块按照镶嵌模式连接,以形成周期性结构;Chen等[24]对广义四折痕折纸的几何力学进行了研究,为材料面内泊松比和面内刚度的逆设计提供了理论基础,并通过三浦折纸进行了验证;Wang等[25]提出了一种新的二维可控孔隙率拉胀材料设计方法,结果表明,花生形孔比椭圆形孔具有更大的泊松比和更小的应力。
相对于负泊松比的结构和材料,变泊松比的结构和材料则更少见。Taylor等[26]提出了一种新方法来设计抗冲击弹性体结构,该结构具有变泊松比特性,故其冲击响应较好,被广泛应用于冲击和保护装置;Fleisch等[27]通过在传统晶胞中引入不对称性,提出了2种泊松比可变的结构;Pratapa等[28]将三浦折纸与蛋壳状折痕相结合,设计了一种名为Morph的折纸机构,可通过改变山谷折痕的分布使折纸机构实现正、负泊松比的切换,并构建了拉伸和弯曲状态下的泊松比计算公式;Khan等[29]基于传统蜂窝网格设计了一种具有可调控泊松比的超材料,并加入了压电材料,实现了泊松比与机电特性的耦合调节。
然而,目前大多数折展机构具有正泊松或零泊松运动特性,具有变泊松运动特性的折展机构极少。为此,笔者以折纸机构为基础,提出一种单闭环厚板支撑单元,并对其支撑刚度进行分析。然后,根据泊松比的定义,设计了一种具有变泊松运动特性的正n边形剪叉式折展机构,并以机构不发生物理干涉为前提,以折展机构可无限纵向扩展为设计目标,基于机构学理论来阐述机构模块化扩展的原理和过程。最后,通过建立折展机构的运动学模型和虚拟样机模型来分析其运动规律及特点。
1 单闭环厚板模型
本文提出了一种正n边形的单闭环折纸模型(n=2ξ+2,ξ∈N*,N*为正整数集),如图1所示。其中:正n边形的外角φ=360°/n。
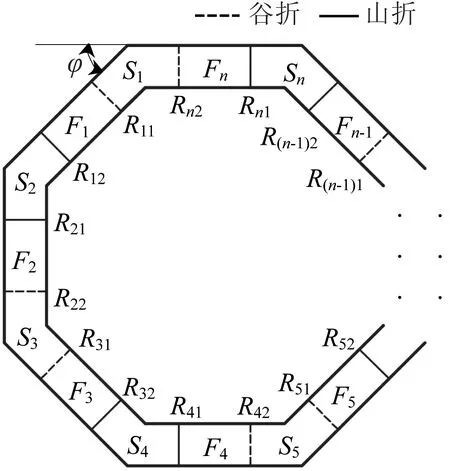
图1 正n边形单闭环折纸模型的折痕分布示意Fig.1 Crease distribution diagram of regular n-sided single-closed-loop origami model
当n=4时,该模型由4个全等的L形纸板和4个全等的矩形纸板组成。4 个L 形纸板的形心Su(u=1,2, …, 4)与正四边形的4个顶点重合;正四边形的4条边可以看成4条支链Lu,支链Lu由1个矩形纸板Fu经转动副Ruv(v=1, 2, …, 4)与相邻2个L形纸板相连,各纸板的连接关系如图2所示。

图2 正四边形单闭环折纸模型Fig.2 Regular quadrilateral single-closed-loop origami model
将图2 所示的折纸模型转化为对应的厚板模型,如图3(a)所示,各个板件均刚性连接且厚度相同,其中θ为L 形板件与矩形板件之间的夹角,且θ∈[0°, 180°]。通过共用板件的方式进行模块化扩展,得到对应的扩展模型,如图3(b)所示。

图3 正四边形厚板模型的扩展Fig.3 Extension of regular quadrilateral thick plate model
正四边形厚板扩展模型可用于三明治结构。目前,三明治结构常用的夹芯层形状主要有几字形、梯形、蜂窝形和拱形等,如图4所示。
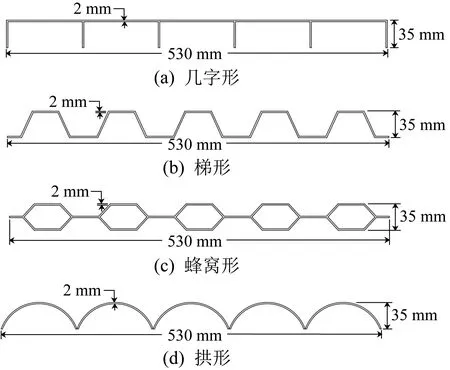
图4 常用的夹芯层形状Fig.4 Common shapes of sandwich layer
三明治结构作为支撑结构应用时须具备较高的刚度,因此对其进行静刚度分析是至关重要的。将4 种常用的三明治结构与夹芯层采用θ=60°,90°和120°(锐角、直角和钝角状态下各取一种)的正四边形厚板扩展模型的三明治结构进行对比分析。各夹芯层均采用相同的材料和结构尺寸,密度、杨氏弹性模量和泊松比分别取7.58×103kg/m3,2.6×106MPa 和0.3,高度、长度和宽度分别为35,530,115 mm。夹芯层为正四边形厚板扩展模型的三明治结构的面板设计参数如表1 所示。4 种常用三明治结构的面板参数与采用θ=90°的正四边形厚板扩展模型的三明治结构相同。在ANSYS Workbench 软件中建立7 种三明治结构的有限元分析模型,在其顶部面板上施加50 N 的均布载荷(方向垂直向下)并进行静力学分析,结果如图5所示。

表1 3种新三明治结构的面板设计参数Table 1 Panel design parameters for three new sandwich structures 单位:mm
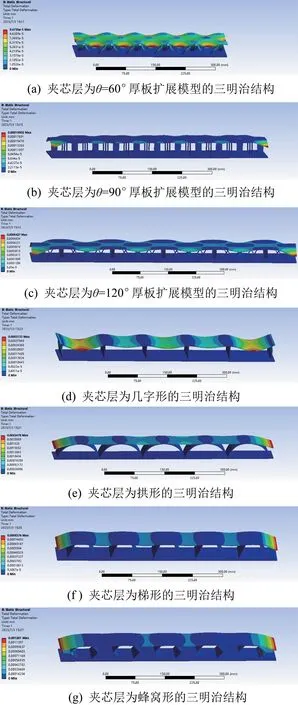
图5 7种三明治结构的变形云图Fig.5 Deformation nephogram of seven sandwich structures
7 种三明治结构的最大应力、最大变形量和夹芯层质量如表2所示。由表2可知,在承受相同载荷的条件下,夹芯层采用正四边形厚板扩展模型时,三明治结构的质量最小且其应力、变形量较小;在夹芯层同为正四边形厚板扩展模型时,在3种波纹形状中,θ=60°时的应力、变形量最小,θ=120°时的应力、变形量最大。
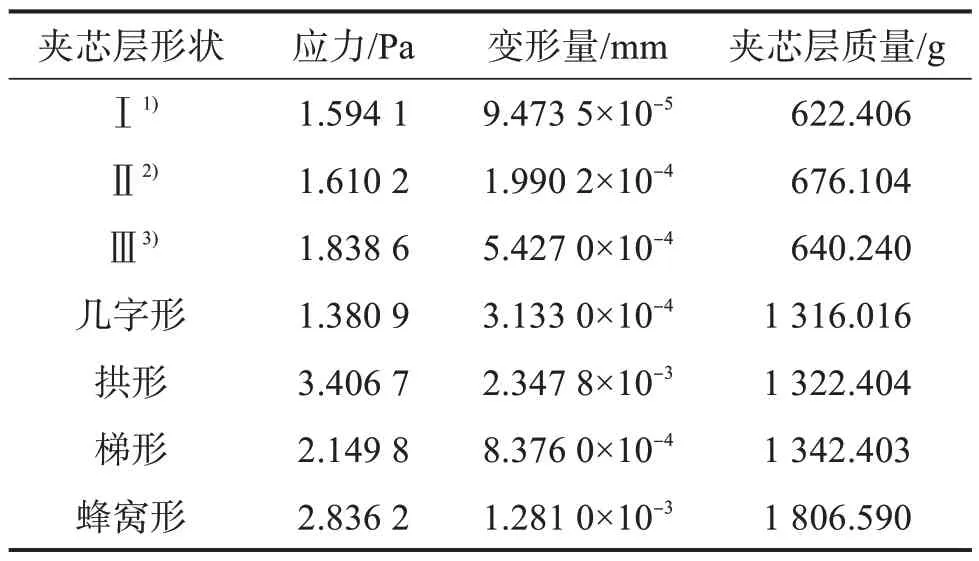
表2 7种三明治结构的最大应力、最大变形量和夹芯层质量Table 2 Maximum stress, maximum deformation and sandwich layer mass of seven sandwich structures
2 具有变泊松运动特性的剪叉式折展机构
2.1 正n边形厚板模型的等效机构模型
通过上文分析可知,夹芯层为正四边形厚板扩展模型的三明治结构具有很好的支撑效果,故对其进行深入研究。分别取4个θ=60°和4个θ=120°的厚板模型组成正四边形支撑结构,在其模型上表面施加50 N 的均布载荷(方向垂直上表面向下),对其进行静力学分析,结果如图6 所示。由图6 可以看出,当θ=60°时,正四边形支撑结构在X和Y方向上均呈“压缩”趋势,即具有负泊松比效应;当θ=120°时,该结构在X和Y方向上均呈“压胀”趋势,即具有正泊松比效应。由此可知,通过改变正四边形支撑结构中θ的大小,即可实现其正负泊松比的改变,即变泊松比特性。
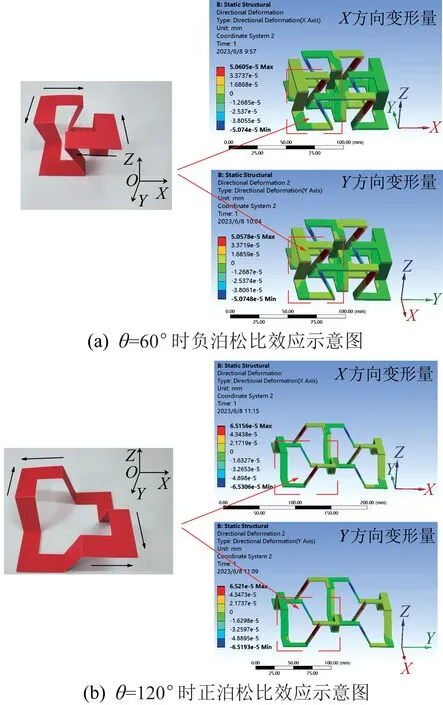
图6 夹角θ对正四边形支撑结构泊松比效应的影响Fig.6 Ⅰnfluence of included angle θ on Poisson's ratio effect of regular quadrilateral support structure
将2个正n边形厚板模型按图7所示的方式构造正n边形剪叉式厚板模型,并在此基础上将其进一步等效为杆件模型,其对应的机构命名为具有变泊松运动特性的剪叉式折展机构。
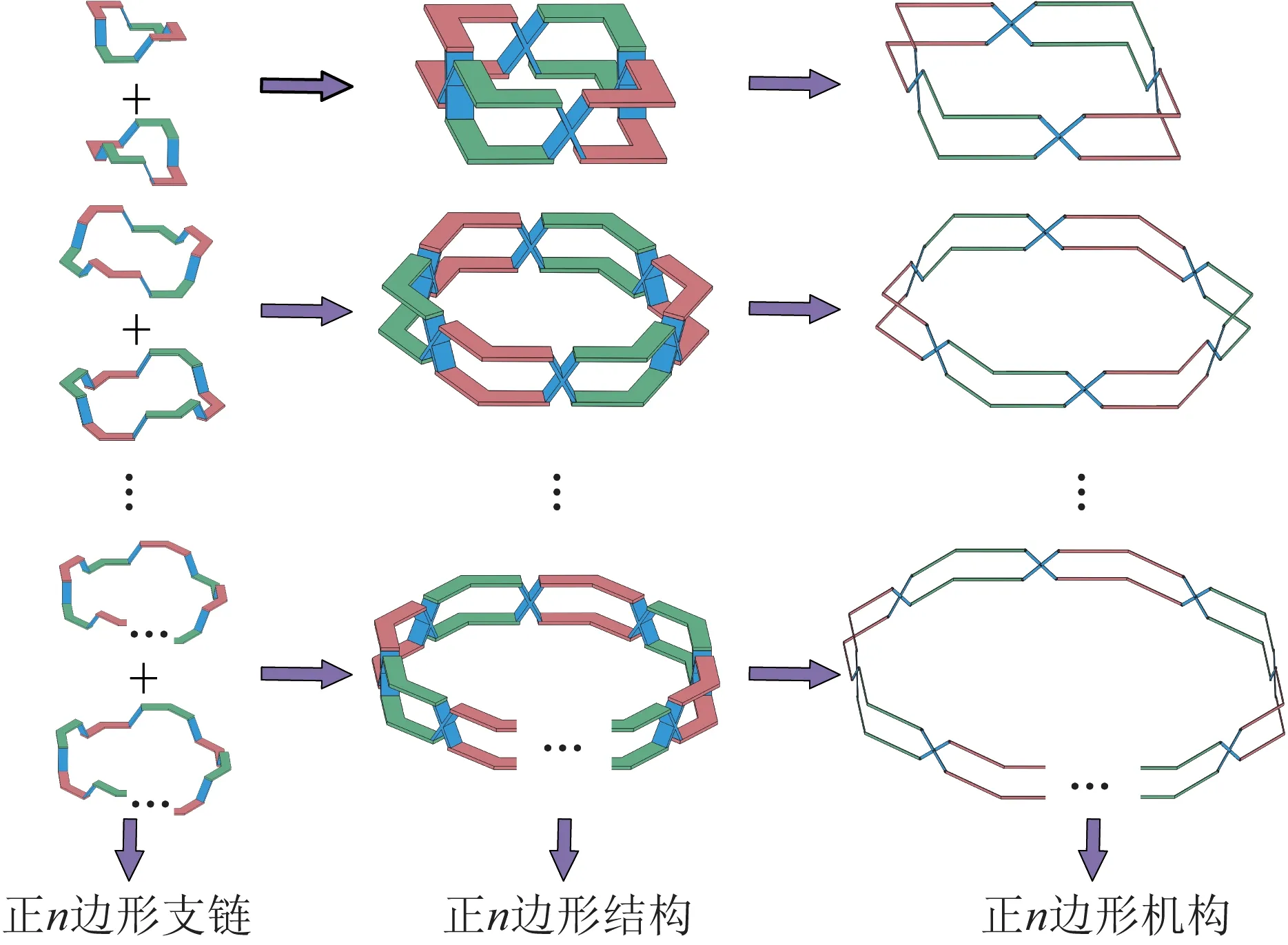
图7 正n边形厚板模型的等效机构模型Fig.7 Equivalent mechanism model of regular n-sided thick panel model
2.2 正四边形剪叉式折展机构有限元仿真
鉴于图7所示正n边形剪叉式折展机构在纵向上的构造相同,选取正四边形剪叉式折展机构为例,对机构的静力学特性进行有限元仿真分析。在折展机构模型上表面的4个杆件上分别施加12.5 N的均布载荷(方向垂直向下),对下表面的4个杆件施加固定约束,仿真分析结果如图8和图9所示。由图8和图9可以看出,正四边形剪叉式折展机构与图6所示的正四边形支撑结构具有相同的变泊松比效应,即当θ=60°时,折展机构在X和Y方向上均呈压缩趋势,即具有负泊松比效应;当θ=120°时,折展机构在X和Y方向上均呈压胀趋势,即具有正泊松比效应。
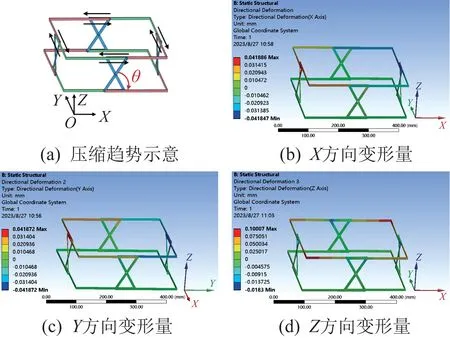
图8 θ=60°时正四边形剪叉式折展机构的负泊松比效应示意Fig.8 Schematic of ngative Poisson' ratio effect of regular quadrilateral scissor deployable mechanism with θ=60°
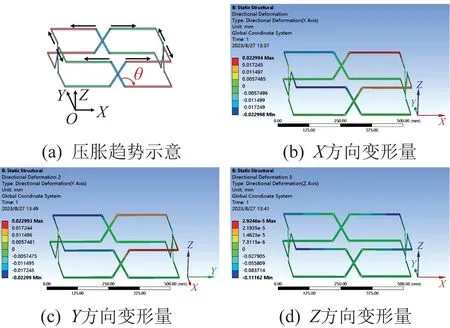
图9 θ=120°时正四边形剪叉式折展机构的正泊松比效应示意Fig.9 Schematic of positive Poisson' ratio effect of regular quadrilateral scissor deployable mechanism with θ=120°
图10所示为θ不同时正四边形剪叉式折展机构在轴向压缩载荷作用下的横向应变。由图10可以看出,该折展机构沿X和Y方向的应变分布几乎一致,且当θ∈(0°, 90°)时,折展机构在对应位姿下的横向应变均小于0,呈压缩趋势,即具有负泊松比效应;当θ∈(90°, 180°)时,折展机构在对应位姿下的横向应变均大于0,呈压胀趋势,即具有正泊松比效应;当θ=90°时,折展机构在对应位姿下的横向应变等于0,即具有零泊松比效应。由此可知,通过改变正n边形剪叉式折展机构中θ的大小,即可实现机构泊松比的调节。
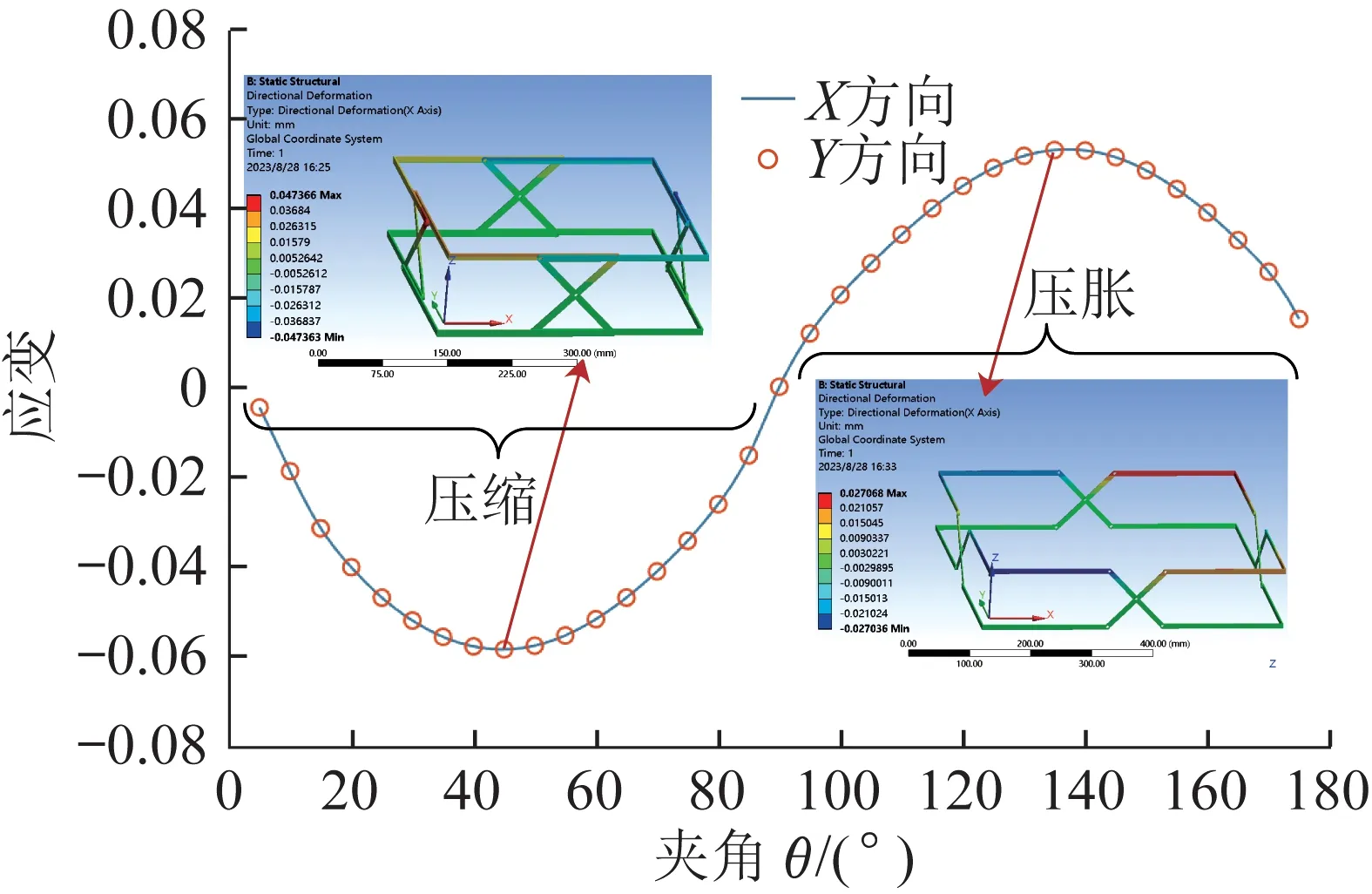
图10 正四边形剪叉式折展机构横向应变的变化曲线Fig.10 Variation curve of transverse strain of regular quadrilateral scissor deployable mechanism
3 剪叉式折展机构运动学分析
3.1 机构自由度分析
为了分析正n边形剪叉式折展机构的自由度,建立其空间笛卡尔坐标系O11X11Y11Z11,如图11 所示(以正四边形剪叉式折展机构为例)。其中:X11轴、Y11轴与底部正四边形的2条邻边重合,其交点为坐标系原点O11,Z11轴由右手定则确定。A1i~E1i(i∈[1,n])为转动副,杆件A11D11与X11轴的夹角为θ,杆件O1iB1i和杆件A1iO1i+1的长度为a,杆件A1iD1i和杆件B1iC1i的长度为b,杆件A1iE1i、B1iE1i、C1iE1i、D1iE1i的长度为c,其中b=2c。
基于图论和螺旋理论,用圆圈表示杆件,线条表示运动副,带数字的运动旋量表示不同关节处的运动,如用$1表示连接杆件A11D11与B11C11的转动副的运动,即可得到具有变泊松运动特性的正四边形剪叉式折展机构的旋量约束拓扑图,如图12所示。
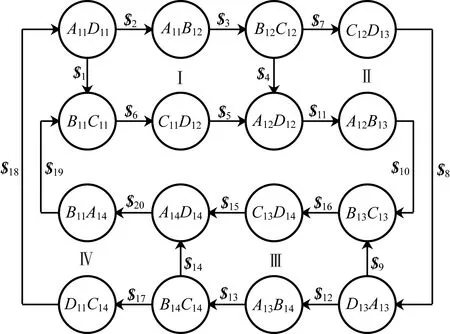
图12 正四边形剪叉式折展机构的旋量约束拓扑图Fig.12 Screw constraint topology graph of regular quadrilateral scissor deployable mechanism
根据连接杆件A11D11与杆件B11C11的转动副1 的空间位置坐标,可得:
式中:r1为转动副1的空间位置矩阵。
则转动副1的转轴所在轴线的方向矢量为:
根据螺旋理论,可得转动副1的运动螺旋,其单位螺旋的表达式为:
同理,可得图12中其他运动螺旋的表达式。定义ωk表示相应转动副的角速度,针对图12中的闭环Ⅰ~Ⅳ,建立相应的旋量约束方程,则可得正四边形剪叉式折展机构的旋量约束方程:
式中:0为六维零向量。
将式(4)写成矩阵的形式,可得:
其中:
由此可知,旋量约束矩阵M为24×20矩阵。正四边形剪叉式折展机构的自由度对应旋量约束矩阵的零空间维数,通过MATLAB软件计算可得:
旋量约束矩阵M的列数为20,其零空间维数为列数减去秩,因此可得正四边形剪叉式折展机构的自由度为1。
3.2 机构模块化扩展
将一系列折展机构单元模块按一定的机构学原理连接在一起,即可构成大尺度折展机构。对于包含m(m≥3)层模块的剪叉式折展机构,(m-2)层中间模块通过共用杆件的方式上下正反交替地安装在顶部模块与底部模块之间,如图13所示。通过模块化叠加,即可实现整个折展机构运动行程的比例放大。

图13 m层正四边形剪叉式折展机构Fig.13 Regular quadrilateral scissor deployable mechanism with m-layer
与传统可展机构相比,上述剪叉式折展机构具有以下优点:
1)仅含转动副,不易出现卡死现象,运动稳定性高。
2)可模块化扩展,通过改变中间模块的数量即可改变整体伸缩量。
3)机构为单驱动输入,便于操作和控制。
4)机构具有变泊松运动特性,其展开时面积大,收缩时面积小。
3.3 机构运动学分析
在m层正n边形剪叉式折展机构中,1个剪叉杆件和4个L形杆件构成一个侧面单元。令第1层正n边形剪叉式折展机构中的第1个侧面单元的体坐标系O11X11Y11Z11为基坐标系,如图11所示,该侧面单元上的点表示为P11;按照逆时针方向,坐标系O12X12Y12Z12为第1 层中第2 个侧面单元的体坐标系,该侧面单元上的点表示为P12,以此类推可得P13、P14、…、P1n;同理,第h(1<h≤m)层中n个侧面单元上的点表示为Ph1、Ph2、…、Phn。在第h层剪叉式折展机构展开过程中,坐标系OhiXhiYhiZhi到Oh(i+1)Xh(i+1)Yh(i+1)Zh(i+1)的变换过程可看作:坐标系OhiXhiYhiZhi从点Ohi平移到Oh(i+1),再绕Zhi轴的正方向旋转φ。在m层正n边形剪叉式折展机构中,点Oh(i+1)在坐标系OhiXhiYhiZhi中的位置矩阵hiOh(i+1)可表示为:
因此,从坐标系OhiXhiYhiZhi到Oh(i+1)Xh(i+1)Yh(i+1)Zh(i+1)的变换矩阵hiTh(i+1)为:
坐标系OhiXhiYhiZhi到O(h+1)iX(h+1)iY(h+1)iZ(h+1)i的变换可看作坐标系OhiXhiYhiZhi从点Ohi平移到O(h+1)i。O(h+1)i在坐标系OhiXhiYhiZhi中的位置矩阵hiO(h+1)i可表示为:
则从坐标系OhiXhiYhiZhi到O(h+1)iX(h+1)iY(h+1)iZ(h+1)i的变换矩阵hiQ(h+1)i为:
根据式(8)和式(10),可得到各单元与各层之间的变换矩阵。再将式(8)与式(10)相乘,可得从基坐标系O11X11Y11Z11到动坐标系OgjXgjYgjZgj(j=2~n,g=1~m)的变换矩阵11Tgj:
在m层正n边形剪叉式折展机构中,动坐标系OgjXgjYgjZgj中任意一点Pgj在基坐标系中的位置矩阵Pgj可表示为:
分别对式(12)求关于时间的一阶导数和二阶导数,可得相应的速度方程和加速度方程:
对于动坐标系OgjXgjYgjZgj中的点Pgj,用vXgj、vYgj和vZgj表示其速度分量,用aXgj、aYgj和aZgj表示其加速度分量,设点P11在基坐标系中的位置矩阵P11=[XP110ZP11]T,根据式(13)和式(14),可得:
设定a=200 mm、b=130 mm,建立3层正四边形剪叉式折展机构的三维虚拟样机模型,通过仿真分析其运动过程,如图14所示。其中,杆件A11D11为驱动杆,在θ∈(0°, 180°)范围内以3 (°)/s的角速度作逆时针匀速转动。根据式(12)至式(16),对该剪叉式折展机构进行运动学建模和编程计算,可得其转动副D32处的位移、速度和加速度曲线,如图15所示。
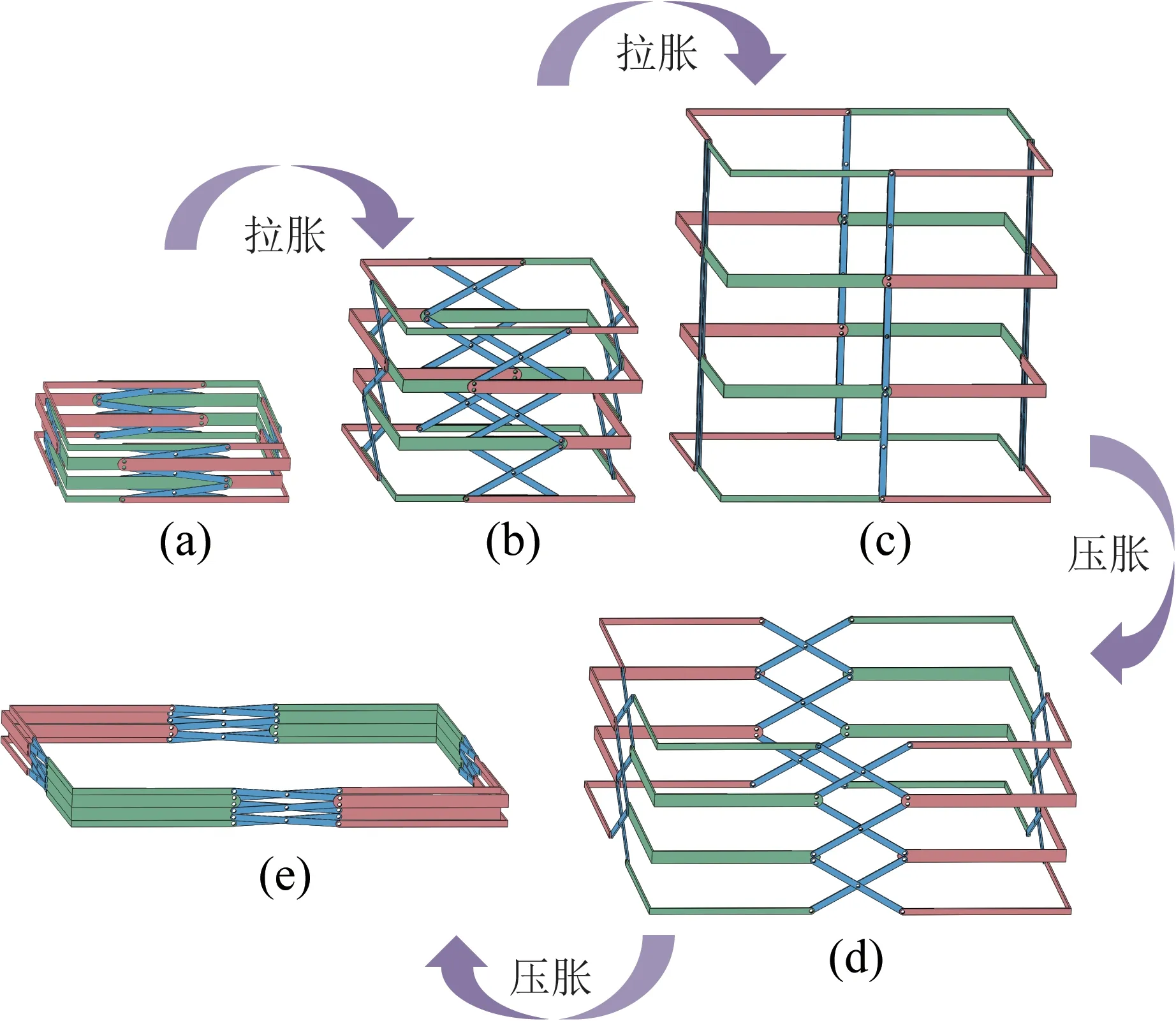
图14 3层正四边形剪叉式折展机构的运动过程Fig.14 Motion process of regular quadrilateral scissor deployable mechanism with three-layer
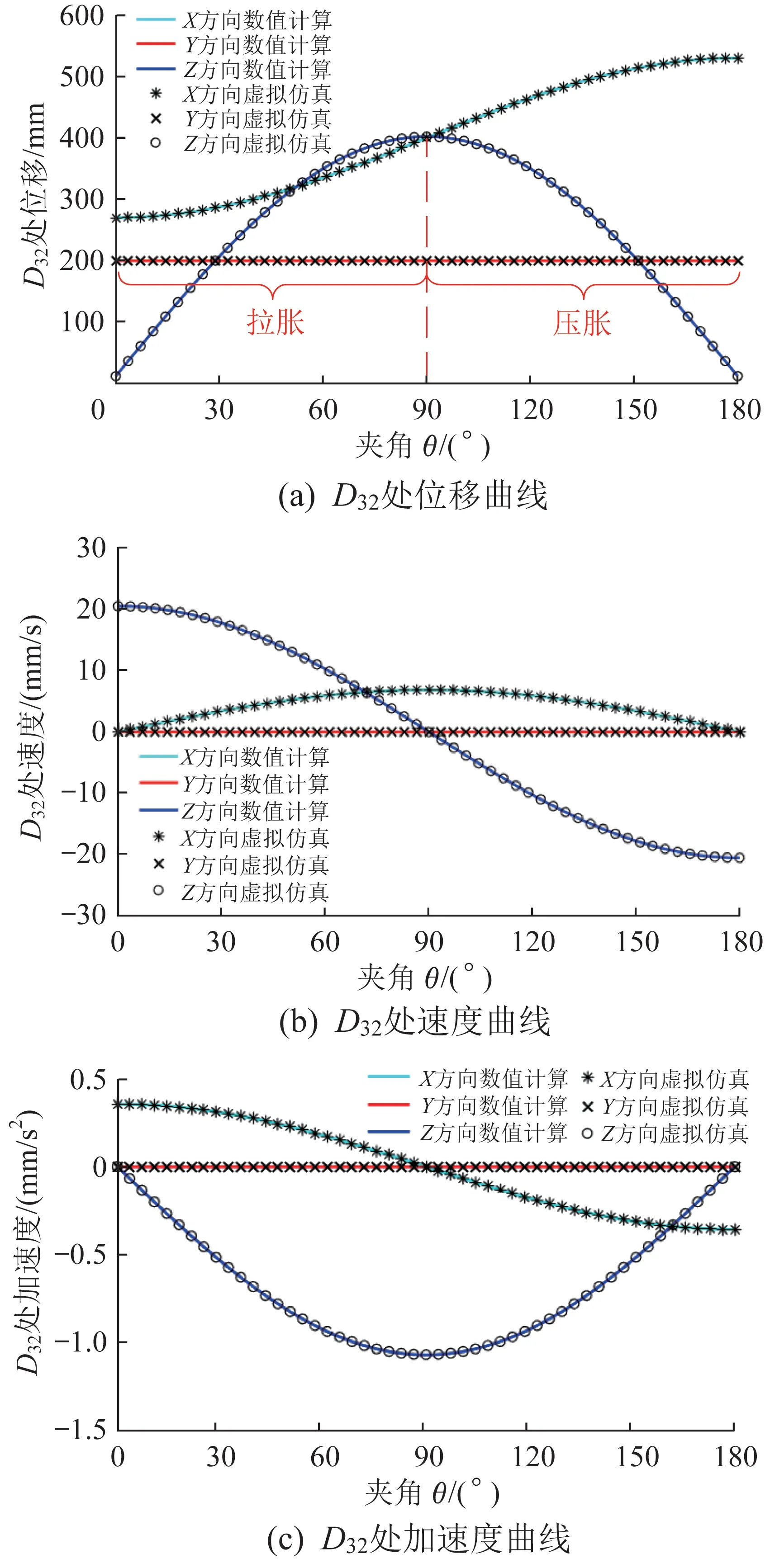
图15 3 层正四边形剪叉式折展机构中转动副D32处的运动规律Fig.15 Motion law at the revolute D32 of three-layer regular quadrilateral scissor deployable mechanism
由图15可以看出,在3层正四边形剪叉式折展机构的运动过程中,其转动副D32沿X方向的位移随着θ的增大而增大,沿Z方向的位移先增大后减小,即当θ∈(0°, 90°)时,机构处于拉胀运动状态;当θ∈(90°, 180°)时,机构处于压胀运动状态。此外,虚拟仿真结果与数值计算结果一致,验证了所建立的运动学模型的正确性和有效性。
3.4 泊松运动特性分析
结合材料力学中关于泊松比的定义[30],对于m层正n边形剪叉式折展机构,令θ=90°时为机构的初始位形,此时机构的外接圆直径mw0和高度mH0为:
当θ从90°减小到0°时,机构处于压缩运动状态;当θ从90°增大到180°时,机构处于压胀运动状态。2 种运动状态下机构的外接圆直径mw和高度mH为:
根据式(17)至式(20),可得机构运动过程中外接圆直径和高度的变化:
根据泊松比的定义[30],机构泊松运动特性的系数νP为:
同样设a=200 mm、b=130 mm,利用式(23)求得m层正n边形剪叉式折展机构的泊松运动特性系数,如图16所示。由图16可以看出,当θ∈(0°, 90°)时,折展机构处于“负泊松”运动状态;当θ∈(90°, 180°)时,折展机构处于“正泊松”运动状态,且折展机构的泊松运动特性系数与其层数和多边形边数无关,只与L 形杆件的几何参数a以及剪叉杆件的几何参数b有关。此外,当θ趋近于90°时,折展机构的泊松运动特性系数趋近于无穷大,即在θ=90°的δ邻域(90°-δ, 90°+δ)内,折展机构很小的高度变化即可引起较大的横截面尺寸变化。
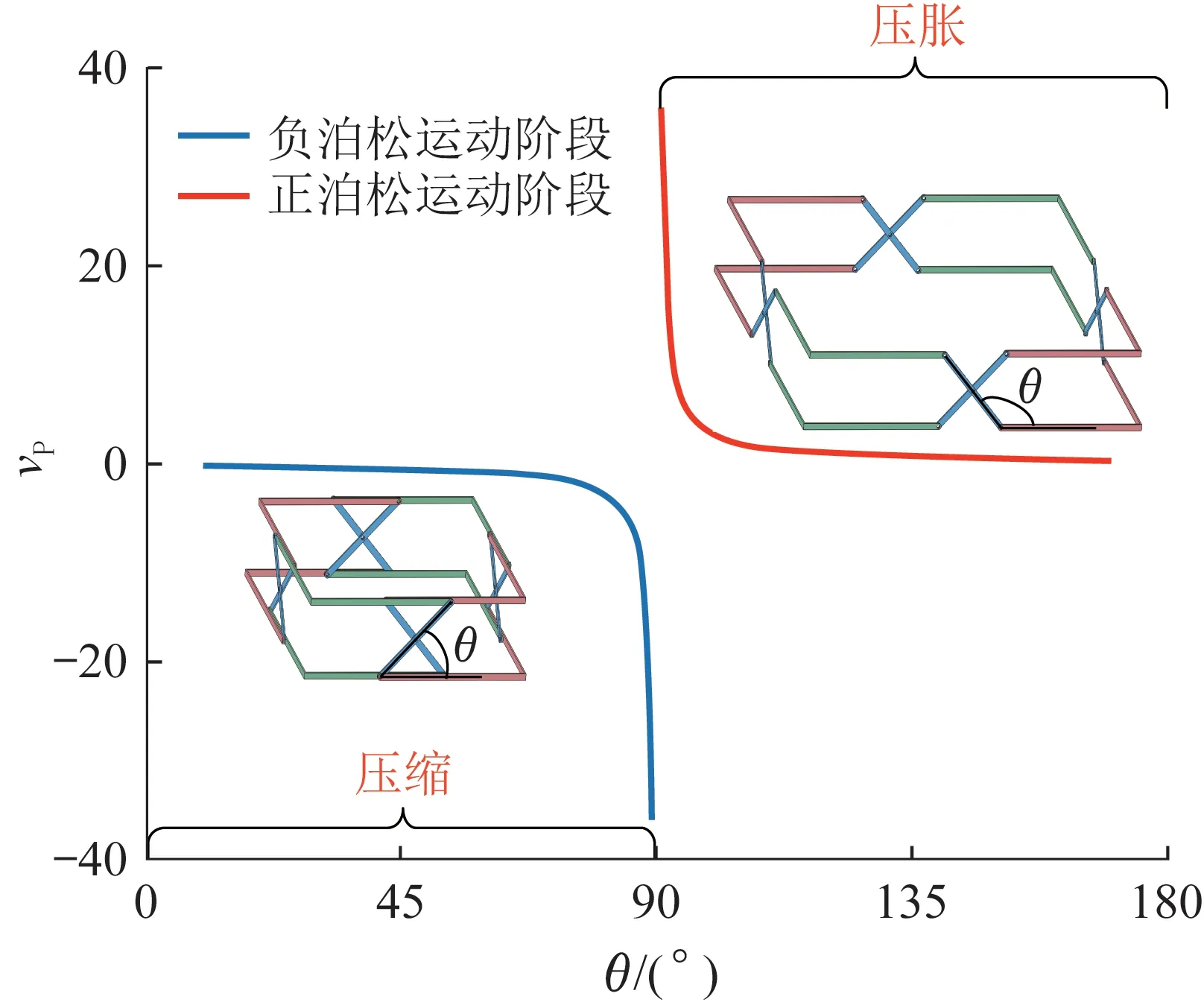
图16 正n 边形剪叉式折展机构泊松运动特性系数的变化曲线Fig.16 Variation curve of Poisson motion characteristic coefficient of regular n-sided scissor deployable mechanism
综上所述,随着θ的变化,正n边形剪叉式折展机构可实现泊松运动特性的变化。由2.1和2.2节可知,机构在任意角度处锁定时,可形成对应的剪叉式折展支撑结构,θ∈(0°, 90°)时的支撑结构具有负泊松比特性,θ∈(90°, 180°)时的支撑结构具有正泊松比特性。因此,正n边形剪叉式折展机构可以通过变泊松运动实现支撑结构的变泊松比特性。基于3D打印技术搭建了正四边形支撑结构与正四边形剪叉式折展支撑结构的实物样机,分别如图17 和图18所示。

图17 正四边形支撑结构样机研制Fig.17 Development of regular quadrilateral support structure prototype
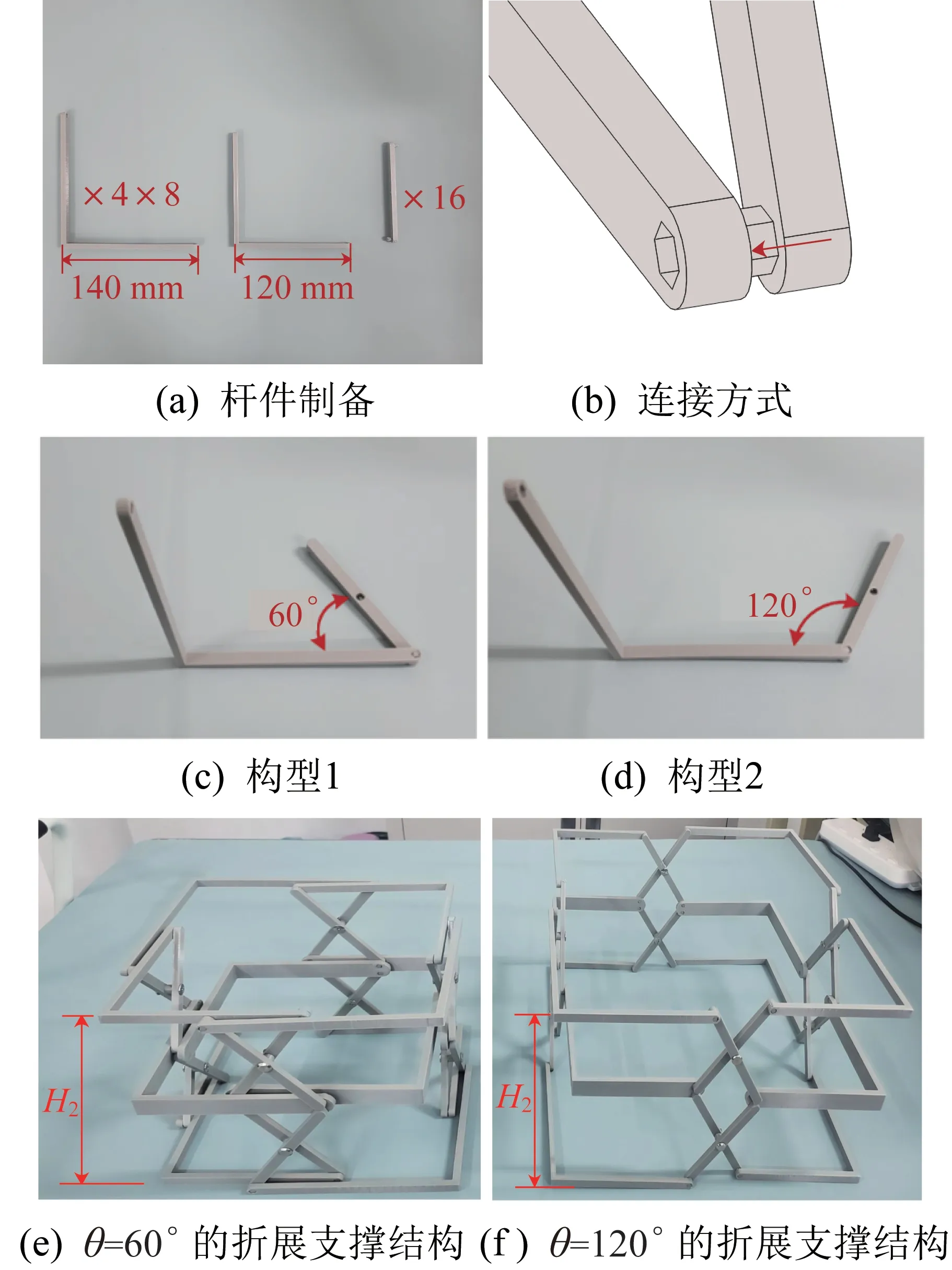
图18 正四边形剪叉式折展支撑结构样机研制Fig.18 Development of regular quadrilateral scissor deployable support structure prototype
4 结 论
1)根据三明治结构的特点,提出一种正n边形分布的单闭环折纸模型,将折纸模型转化为厚板模型,通过共用板件的方法进行模块化扩展。运用ANSYS Workbench软件对7种三明治结构进行有限元分析,得到夹芯层为正四边形厚板扩展模型的三明治结构的支撑刚度较大且质量最小。
2)运用图论和螺旋理论,计算得到正四边形剪叉式折展机构的自由度为1;基于机构模块化组成原理,阐述了机构模块化纵向扩展的过程,并构造了具有变泊松运动特性的m层正n边形剪叉式折展机构。
3)运用变换矩阵法建立了剪叉式折展机构的运动学模型,提出了描述机构泊松运动特性的系数,并以3层正四边形剪叉式折展机构为例,基于数值计算和虚拟仿真技术验证了所构建的运动学模型的正确性。
4)提出了一种可实现支撑结构变泊松比特性的方法,并运用3D打印技术搭建了正四边形支撑结构与正四边形剪叉式折展支撑结构的实物样机,验证了所提出方法的可行性,这可为后续的研究提供理论基础。
