无失效威布尔情形下基于双修正多层Bayes的可靠性评估

龙足腾， 郑 波,2， 甯 洋， 罗金超

（1. 中国民用航空飞行学院 航空电子电气学院， 四川 广汉 618307；2. 核工业西南物理研究院， 四川 成都 610225）

随着工业化、现代化的发展，越来越多的产品表现出高质量、高可靠性、长寿命及短期内无失效的特性。在这类产品的可靠性试验中，经常出现无失效的情形，很难通过定时或定数截尾试验获取其完全失效数据来进行可靠性分析，这不仅增加了产品研发的时间和成本，还会严重阻碍产品的后续定型及应用。因此，产品无失效情形下的可靠性评估研究具有很强的实际意义，是当下可靠性领域的研究重点。

Martz等[1]是最早开始研究无失效数据处理的学者，提出了一种以失效概率为指标，结合Bayes理论的可靠性评估方法。随后，茹诗松等[2]提出了配分布曲线法，通过估计无失效数据各个截尾时刻的失效概率，找到失效概率与寿命分布函数之间的关系，用最小二乘法配一条分布曲线，得到可靠度函数。由于配分布曲线法流程清晰，计算相对简便，估计效果稳定，在无失效数据的可靠性研究和实际工程中得到广泛应用。

配分布曲线法的关键是估计失效概率，相关学者就失效概率的估计进行了深入的研究，一些成熟的Bayes方法被相继提了出来，如多层Bayes[3]和EBayes 法[4-5]。这些方法在试验中得到验证，证明了能够用于无失效情形的分析[6-7]。随后，它们在处理不同寿命分布类型的无失效数据中成为主流方法，尤其在威布尔分布情形的研究中得到广泛的认可[8-11]。一些学者和研究人员通过结合各种估计原理和算法来构造可靠性评估模型，从而解决实际工程问题[12-14]。在实际应用中，超参数和试验分组等影响可靠性评估精度的问题被引入研究，推动了主流Bayes方法在工程问题中的应用[15-16]。

随着研究的深入，一些学者发现基于多层Bayes和E-Bayes的估计效果较于保守，于是通过引入Bootstrap法的区间估计或融合多源信息数据来提高模型估计的精度和可信度。李海洋等[17-18]利用EBayes 法完成点估计，通过引入参数Bootstrap 法完成区间估计并构建融合模型用于机器人轴承可靠性评估，并且在对扭转电机实际运行后的无失效数据的分析中取得了良好的估计效果；王瑞祥等[19]利用多层Bayes完成点估计，再结合Bootstrap构建小样本无失效的可靠性评估模型；Chen等[20]针对航空发动机压气机盘的小样本无失效数据，在Bayes估计的基础上采用了融合测试数据与模拟数据的评估思路。极少数学者旨在改进Bayes 估计，如：李爽等[21]在威布尔分布失效概率估计时，利用后验分布调整先验分布来修正失效概率的取值上界，提出了一种基于多层Bayes的改进方法，将它用于提高失效概率估计精度。

综上所述，利用配分布曲线处理无失效情形下可靠度点估计时，E-Bayes和多层Bayes是估计失效概率的主流方法，但其估计效果相对保守。为了提高失效概率的估计精度，本文通过改进多层Bayes，提出双修正多层Bayes，并结合加权最小二乘法和可靠度函数完成可靠度点估计；通过仿真试验和工程实例分析，来验证新模型的可行性和有效性；最后，讨论了双修正多层Bayes的适用性。

1 无失效数据与威布尔分布

1.1 无失效数据结构

在工业产品中，随机抽取n个样本，将它分成k组，进行定时截尾试验。各组样本数分为n1,n2, …,nk，截尾时间为t1,t2, …,tk(t1＜t2＜…＜tk)。若在试验中无一样本失效，则称该样本组数据为无失效数据，有n=n1+n2+…nk(i=1, 2, …,k)。无失效数据的结构如表1所示。表中未失效数si（si=nk+nk-1+…+ni） 即试验中截尾时间ti时刻的未失效数。

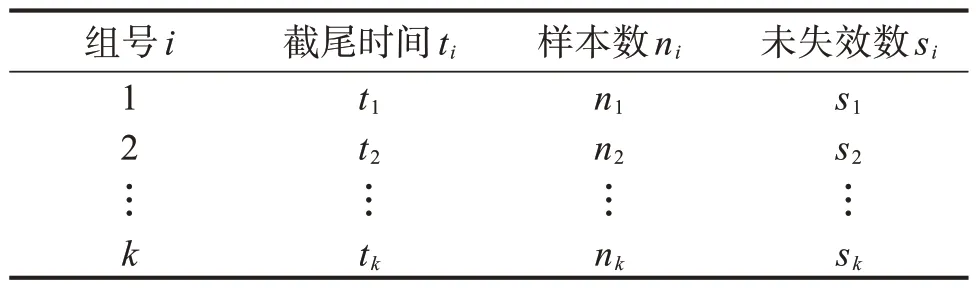
表1 无失效数据结构Table 1 Zero-failure data structure

1.2 威布尔分布

许多工业产品如机械零部件、电子元器件的寿命能够拟合成威布尔分布。威布尔分布的形状参数能很好地反映产品失效特性，可以根据其值大小判定产品的失效类型，因此威布尔分布对各类型的试验数据具有较强的适应能力，在可靠性研究领域有着广泛应用。

本文选取两参数参威布尔分布作为研究对象。其失效概率密度函数为：

失效分布函数为：

失效率函数为：

可靠度函数为：

式中：β为形状参数；η为尺度参数或特征寿命（即可靠度R=0.367 9时的寿命值），它决定了曲线尺寸比例的大小，能够缩放坐标尺度，并且受负载影响，负载越大，η越小。

形状参数β对威布尔分布函数的影响如图1所示。

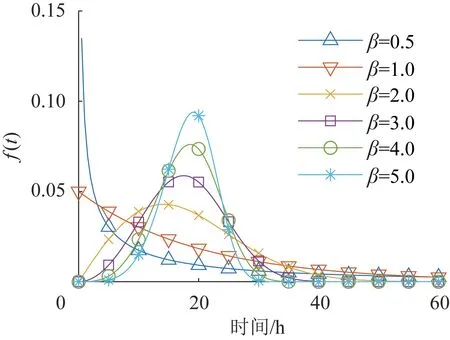
图1 形状参数β对威布尔函数的影响Fig.1 Ⅰnfluence of shape parameters on Weibull functions

由图1 可知，当β=3.0～5.0 时，威布尔分布函数图像与正态分布图像很相似。

2 无失效威布尔可靠度估计

2.1 失效概率pi的多层Bayes估计

无失效数据在某一时刻ti处的失效概率pi值较大的概率很小，pi值较小的概率很大，因此取pi的先验分布为共轭Beta 分布，其概率密度函数为：

式中：0＜pi＜1；B(a,b)为Beta函数；a和b为超参数且相互独立，一般为了保证其密度函数为减函数以及Bayes 估计的稳健性；设0＜a≤1，1＜b＜c，c为常数，根据文献[16]，c通常为整数，在2～7 中选取。

超参数a和b的先验分布为：

由式(5)、式(6)可得pi的多层先验分布为：

由于所得数据是无失效数据，pi的似然函数为：

根据Bayes定理，由式(7)、式(8)可得pi的多层后验分布密度函数为：

在平方损失下，取多层后验分布的期望作为pi的多层Bayes估计，可以表示为：

为了简化计算，根据工程建议[19]，取a=1，则计算得，从而得到pi多层Bayes的解析式为：

2.2 失效概率pi的双修正多层Bayes估计

由于在无失效场合下，pi始终满足0＜pi＜1，无法取到0和1，因此考虑通过修正pi的取值范围来减小估计误差。根据Bayes 修正理论[21]，后验分布是对先验分布的修正与调整，将其用于估计pi的基本思路是：利用前一时刻pi的后验分布替代后一时刻pi的先验分布。

设pl、pu分别为pi的下限值和上限值，则0＜pl＜pi＜pu＜1，此时Beta分布就不能很好地描述pi的先验分布。考虑选用不完全Beta 分布，其相较于Beta分布图像更加集中，这就意味着pi的取值区间变小，误差波动也变小。不完全Beta函数的表达式为：，式中：x1和x2分别对应pl和pu。在多层Bayes 的基础上，通过改变先验分布，可以得到双修正多层Bayes的表达式，如下所示。

1）失效概率pi估计。

根据不完全Beta分布函数，得其先验密度函数为：

其似然函数为：

根据Bayes定理，得其后验分布密度函数为：

在平方损失下，对后验分布取期望得到pi的估计为：

取a=1，简化式(15)，可得：

2）修正失效概率上限值pu。

根据截尾时间正序ti(t1,t2, …,tk)，设初始时刻t1的失效概率符合Beta分布，即失效概率取值范围为(0, 1)。计算t1时刻失效概率上限值pu1，将其作为下一时刻t2的失效概率下限值，然后得到t2时刻失效概率上限值pu2并作为t3时刻失效概率下限值，依次进行至tk时刻，将得到的失效概率上限值集合pu1,pu2, …,puk作为上限，对应式(16)中的pu，即：

式中：pui为第i时刻的失效概率上限值。

3）修正失效概率下限值pl。

式中：ascend[·]为升序排列，pli为第i时刻的失效概率下限值。

2.3 参数估计及可靠度计算

式中：ωi为权重。根据文献[16]可知，以总试验时间设计权重，估计效果最好，则：。

3 验证分析

3.1 Monte-Carlo仿真数据

为了验证新方法的估计效果，需要进行大量的对比试验。利用Monte-Carlo 法可以有效地仿真试验数据，便于评估分析。其详细仿真方法参考文献[19]的做法：由计算机生成700个服从威布尔分布的随机数（产生的随机数要远多于试验产品样本数，本文取产品样本数为28个），并将随机数从小到大排列，然后以每10 个数据为一组，共分为70 组数据，对其中前7组数据中的首个数据向下取整，可得到7组截尾时间，样本在截尾时间下均没有发生失效，各截尾时刻的样本数随组号依次递减。

通过前文分析可知，考虑到长寿命机械产品的特性，取β=3，η=2 500，得到一组无失效数据，如表2所示。

表2 仿真的无失效数据Table 2 Simulation of zero-failure data

3.2 仿真结果对比分析

分别采用传统Bayes、E-Bayes、多层Bayes 和双修正多层Bayes对表2数据进行运算，得到失效概率估计值，如表3所示。由表可知，E-Bayes和多层Bayes方法下失效概率估计值相差不大，后者略优，但两者均优于传统Bayes，而本文方法在1 049 h前最接近真值。

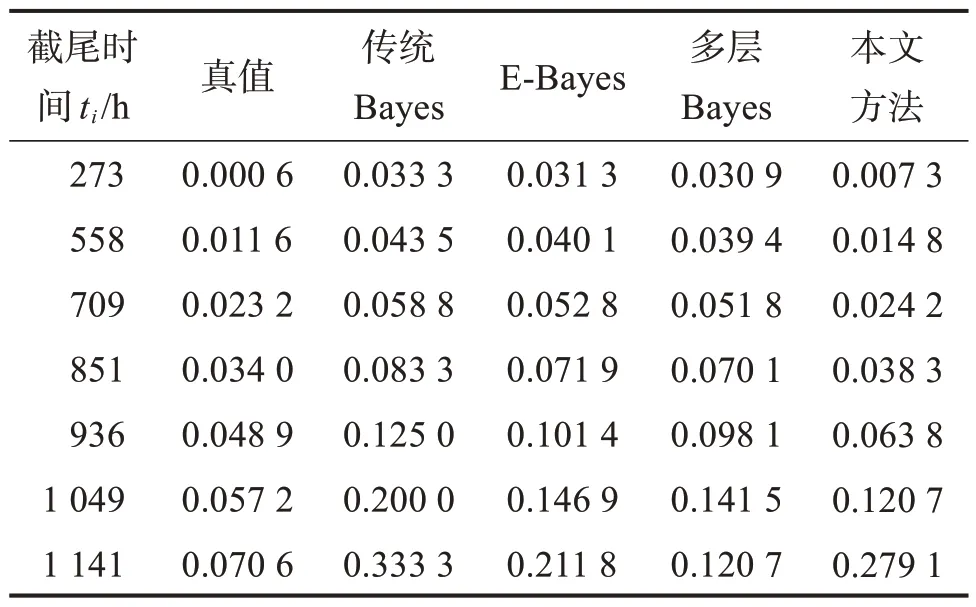
表3 不同方法下的失效概率估计值Table 3 Estimation of failure probability under different methods

将表3数据代入式(19)，并取超参数c=5，得到各方法下的β和η，并计算其与真值之间的相对误差Emr.β和Emr.η，结果如表4 所示。由表可知：E-Bayes和多层Bayes的估计误差均在40%左右；传统Bayes对η的估计效果较好，但对β的估计较差；本文方法对β和η的估计误差均较低并且较均衡，控制在6.3%左右。

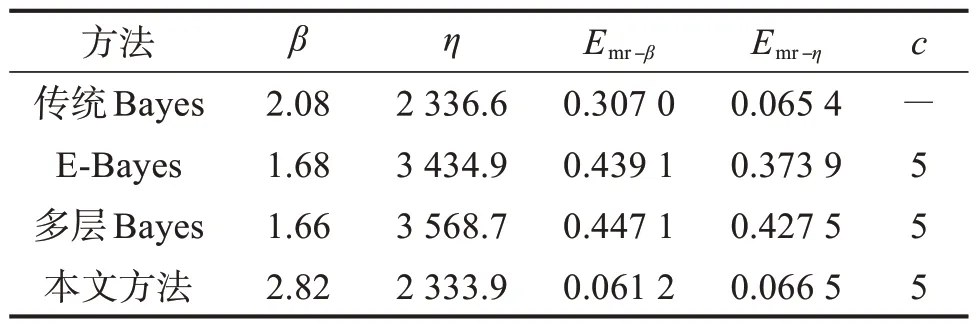
表4 不同方法下的参数估计及其相对误差Table 4 Parameter estimation and relative error under different methods

将表4 数据代入式(20)，得到各方法下的可靠度，如图2所示。由图可知：采用本文方法得到的可靠度更加接近真值，且其鲁棒性更好；在1 200 h内任意时刻的可靠度均优于其他Bayes方法。

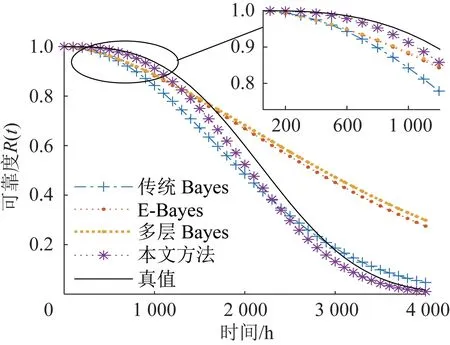
图2 不同方法下的可靠度Fig.2 Reliability with different methods

3.3 工程实例分析

航空陀螺仪是一种非常精密的导航仪器，其中轴承是其关键的机械零部件，轴承失效会直接导致陀螺仪发生工作故障。因此，对陀螺仪的轴承进行可靠性评估是极为重要的。采用文献[16]提供的某轴承无失效数据，如表5所示，分别用传统Bayes、E-Bayes、多层Bayes 和本文方法进行可靠性分析。另外，根据相关工程部门提供的信息，该轴承在1 300 h内的可靠度为100%。

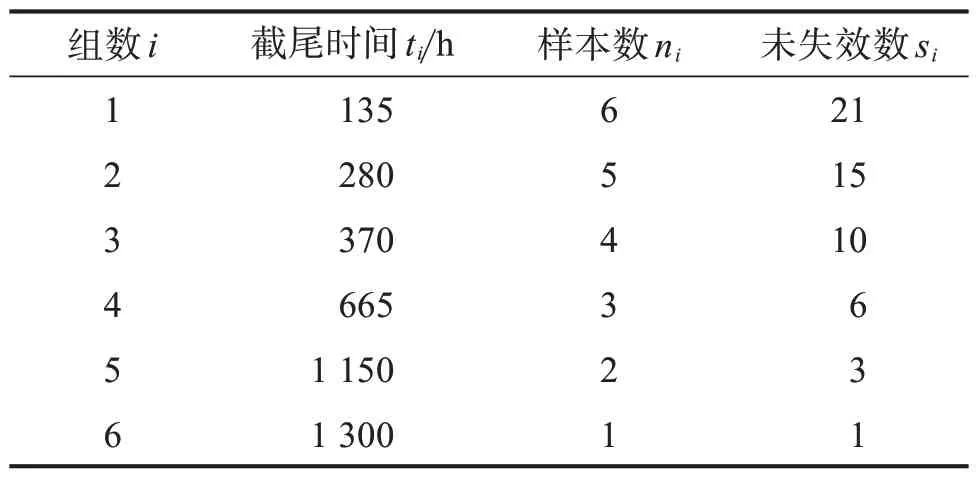
表5 某轴承的无失效数据Table 5 Zero-failure data of a certain bearing

估计精度受超参数c的影响，故讨论当c=4～7时各方法的估计效果和稳健性。c=4～7 时轴承的可靠度如图3所示。

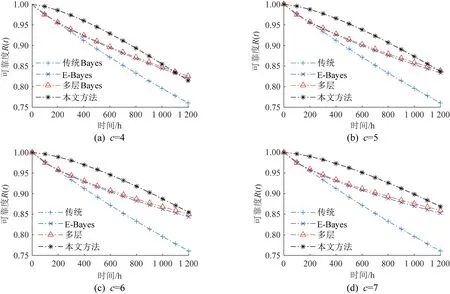
图3 在c = 4～7时轴承的可靠度Fig.3 Reliability of bearings when c = 4～7

由图3可知：

1）当c=4～7时，从总体上来看，4种方法按可靠度估计精度从大到小的排序依次是本文方法、E-Bayes、多层Bayes 和传统Bayes，本文方法估计的结果更加接近实际值，且其具有良好的稳健性。

2）当c=4时，本文方法在1 100 h以前的可靠度估计效果好于E-Bayes和多层Bayes，1 100 h以后逐渐出现差于多层Bayes和E-Bayes的趋势。

3）在试验组数不变的情况下，c值越大，各方法的估计效果越好。

4 双修正多层Bayes的适用性分析

以上验证结果表明了本文方法的估计效果较好，但在实验过程中存在着一定的偶然性和局限性，主要体现在利用Monte-Carlo 法生成呈威布尔分布的无失效数据时须提前设置β和η，因此仅能体现本文方法在某一特定条件下的优势。为了验证本文算法的适用性，分析当β=1.4～5.0，η=1 500～13 500时双修正多层Bayes结合加权最小二乘法的参数估计效能。利用Monte-Carlo 仿真试验，循环10 000次，输出结果为相对误差平均值，具体试验流程如下图4所示。

图4 适用性分析的试验流程Fig.4 Experimental process for applicability analysis

运用定量分析法讨论本文方法随威布尔双参数变化的可靠度估计能力,并与E-Bayes、多层Bayes方法进行对比。设置η=2 000，得到β变化时各方法的估计效果，结果如图5所示。设置β=3，得到η变化时各方法的估计效果，结果如图6所示。

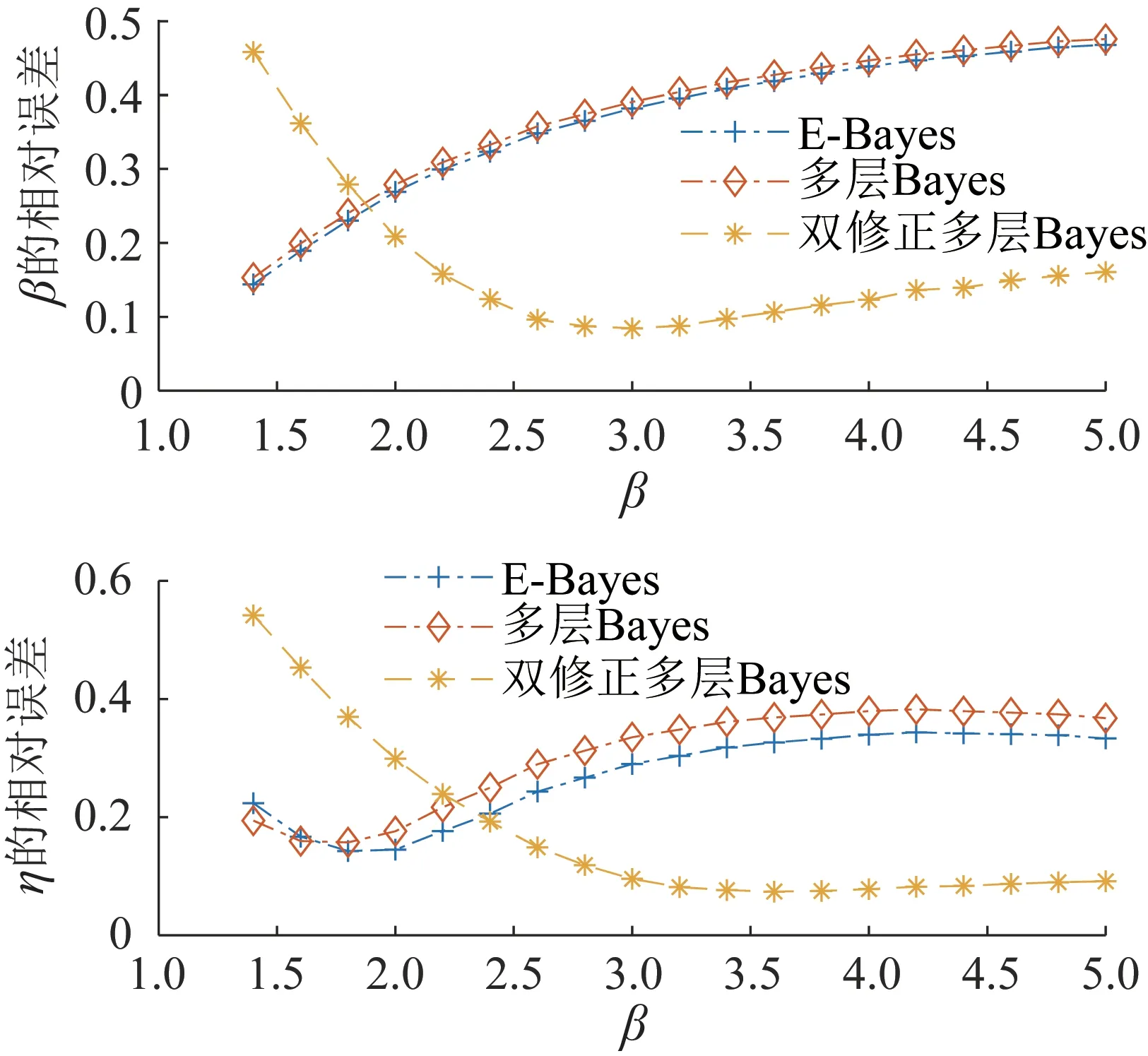
图5 各方法估计β的相对误差Fig.5 Relative error of each method to estimate β

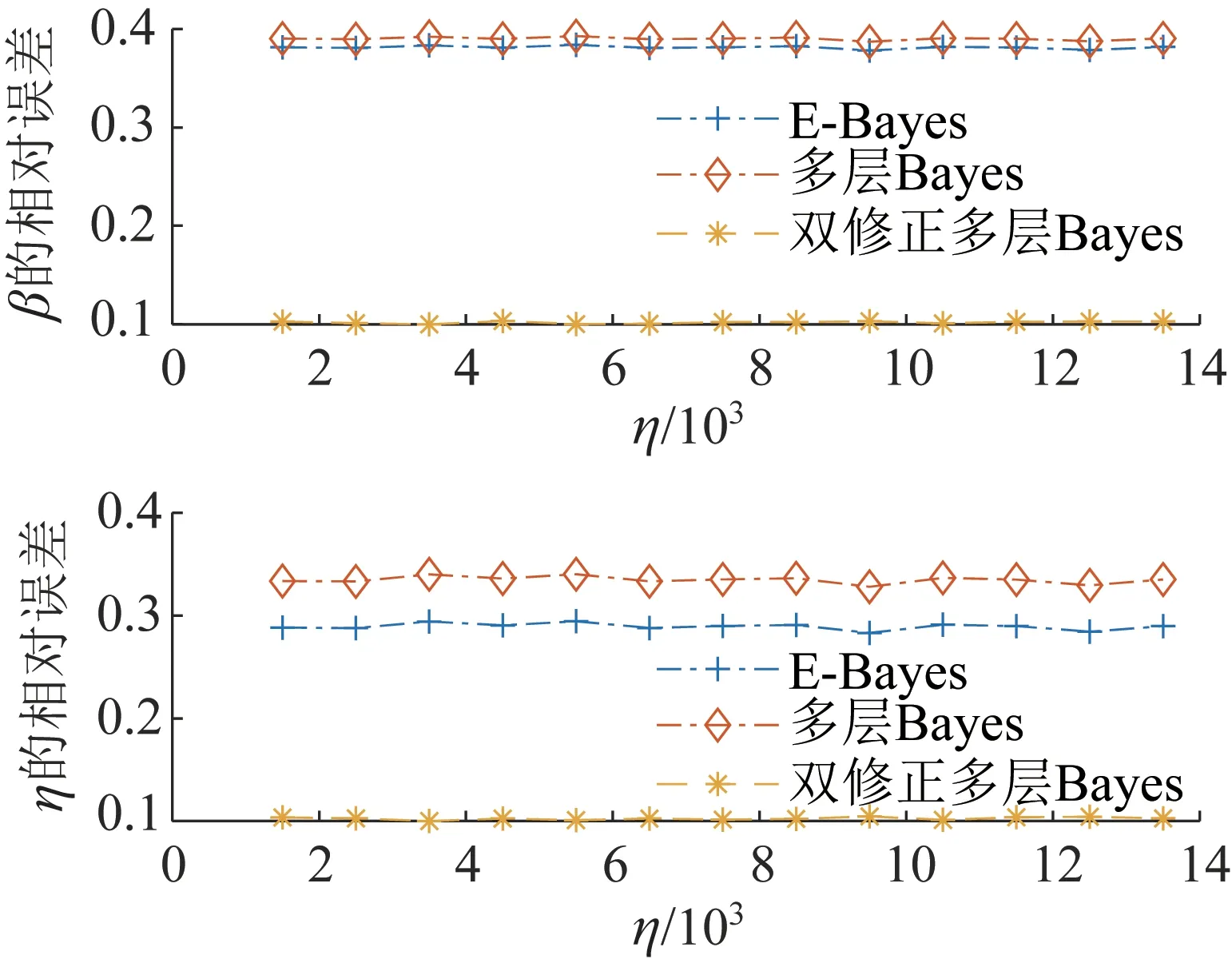
图6 各方法估计η的相对误差Fig.6 Relative error of each method to estimate η

由图5和图6可知：β会影响各Bayes的估计效果，而η几乎不会产生影响；多层Bayes和E-Bayes的估计误差随着β的增大而增大，在β=1.5 左右时估计效果最好，相对误差控制在20%以下，较本文方法更有优势；本文方法在β＞2.2时的估计效果优于E-Bayes和多层Bayes，在β=3左右时估计效果最好，相对误差在10%以下，在β＞3时Emr-β出现增大的趋势，而Emr-η基本不变，总体效果仍显著优于E-Bayes 和多层Bayes，且较它们具有更宽的适用区间。

5 结 论

为了提高对威布尔分布无失效数据的可靠度点估计精度，本文提出了双修正多层Bayes方法来估计失效概率并完成可靠度评估，得出如下结论：

1）双修正多层Bayes方法能有效改善失效概率的估计精度，尤其在结合加权最小二乘法后，能将威布尔双参数估计的相对误差控制在10%以下。

2）以双修正多层Bayes方法为核心，结合加权最小二乘法，能够有效进行参数估计和可靠度估计，并具有较高的精度和良好的稳健性。

3）通过适用性分析发现，双修正多层Bayes的估计精度更高，且适用范围更宽，尤其对于β＞2.2的威布尔分布数据，较主流Bayes方法有显著优势。研究结果可以为其他寿命分布无失效数据的可靠性评估提供参考。