火工品柔性结合关键部件静力学分析及收口压力优化设计

2024-03-08丁铮杰车英

长春理工大学学报（自然科学版） 2024年1期

丁铮杰，车英

（长春理工大学光电工程学院，长春 130022）

合格的收口工艺可提高火工品的可靠性，因此收口技术的重要性不言而喻。安岩等人［1］通过柱塞组件收口的方法，实现柱塞座与柱塞杆之间的灵活无紧涩，并通过拉力试验机检测拉伸后收口工件。丁亚昕等人［2］针对UG6 轴承建立了轴承安装固定工艺分析的有限元模型，模拟了压装、收口、拉脱全过程轴承和轴承座变形情况，研究了过盈量、摩擦因数、收口深度以及材料参数对分解力的影响。但目前的收口研究中，均是采用硬收口装置，易伤害到收口工件，产生划伤、凸起等弊端。目前还未有专门针对软收口装置及油压与被收口部件的分解力关系进行的研究。

本文基于ANSYS Workbench 建立了软收口装置的轴对称模型，对无杆油缸压缩模具的收口结合部分进行静力学分析，通过选择不同材料的橡胶环，来判断同种工况下，工件结合部分的优劣，并通过拉力试验机进行火工品分解实验，得出油压p、橡胶环压力F1与火工品分解力F2的对应关系。

1 柔性结合装置有限元模型的建立

1.1 几何模型的建立

以火工品柔性结合机构的关键部件作为研究对象，与橡胶圈直接接触对其施加力的零件，包括药筒、橡胶环套、压环。被结合工件需达到的最终效果如图1 所示。

图1 收口结合需达到的最终效果图

鉴于边界条件的复杂性以及几何模型的特殊性，可将其简化为平面轴对称问题［3］。建立的二维几何模型如图2 所示，其中梯形橡胶环的上底为15 mm，下底为36 mm，高为25.5 mm；药筒壁厚为2 mm；收口槽为一个上底8 mm，下底14 mm，深为2.5 mm 的梯形。

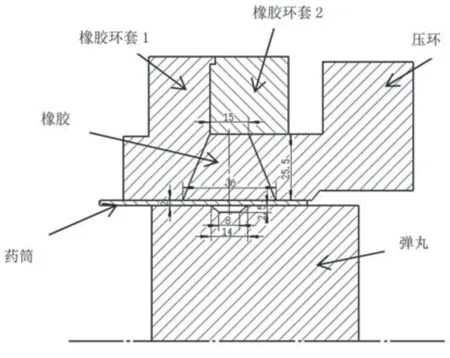
图2 柔性结合装置的二维模型

使用solidworks 对其进行三维实体建模（如图3 所示）。保存为xt 格式导入Workbench 的Geometry模块，在Geomrtry 中将其转化为二维模型，进行研究。文章柔性结合装置中，药筒材料为黄铜，其屈服强度为274 MPa，杨氏模量为137 000，切变（正切）模量为629，泊松比为0.3。

图3 柔性结合装置三维建模

1.2 有限元分析的非线性理论以及材料的参数属性

由于橡胶具有各向同性和体积近似不可压缩的特点［4］，因此在工程方面普遍采用应变能密度函数对橡胶材料的超弹性进行表征。而目前在对非线性材料的有限元分析中，多项式应变能密度函数［5］的使用最为广泛，尤其对于橡胶材料等近似不可压缩材料而言，Mooney-Rivlin 应变能函数使用的最为广泛，其应变能函数如下：

式中，C01、C10为材料Mooney-Rivlin 的参数；W为应变能密度；I1、I2为应变张量的两个主不变量。

为使仿真结果更加精确，考虑橡胶材料的泊松比，其不可压缩参数如下：

式中，V为材料的泊松比；C01、C10为材料的Mooney-Rivlin 参数。

文章的柔性结合模具中，弹体可视为刚体材料模型，其和橡胶环套1、橡胶环套2 以及压环材料均选用钢材，杨氏模量为210 000，泊松比为0.3；橡胶将分别对比95 A 聚氨酯橡胶、硅橡胶、三元乙丙橡胶、丁腈橡胶以及氟橡胶在柔性结合过程中的变形情况及结合的效果。张琦等人［5］通过材料试验机进行实验得到了丁腈橡胶、硅橡胶、氟橡胶的应力应变曲线；大连理工大学马骥等人［6］对聚氨酯冲模模具进行探索，得到了不同硬度下的聚氨酯橡胶的压缩应变曲线；华南理工大学姚润樾等人［7］对三元乙丙橡胶进行单轴拉伸实验，得到了三元乙丙橡胶的拉伸伸长应力与拉伸伸长率之间的关系。应力-应变曲线数据通过Workbench 软件Engineering data 模块可拟合得到，通过公式（2）可以计算出该五种材料的不可压缩参数d，五种材料的泊松比均取为0.47，得到该五种材料的相关参数，如表1 所示。

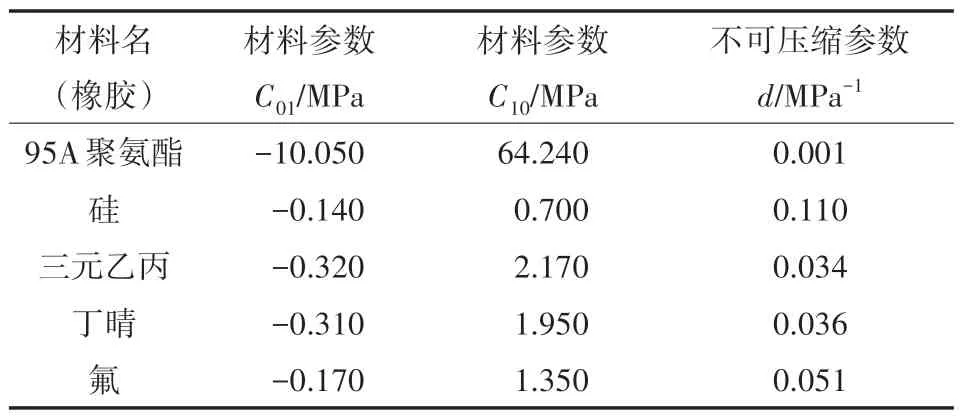
表1 柔性结合装置橡胶环仿真材料参数汇总

1.3 接触方式、网格划分和加载方式

划分网格时，因主要研究的对象为橡胶环和药筒的应变、应力情况，故需要对其进行加密划分以增强最终求解结果的精确程度，并采用六面体单元类型［8］，其他的网格划分采取默认划分即可。

网格划分后的有限元模型如图4 所示。

图4 柔性结合装置网格划分结果

在柔性结合装置的模型接触分析中，根据实际情况采用面-面接触，其中，橡胶环套1 和橡胶环套2 采用绑定接触，设置橡胶环表面为接触面，橡胶环套1、橡胶环套2、压环以及药筒外表面为目标面，接触类型设置为摩擦接触，且摩擦因数设置为0.2［9］。

根据收口装置在实际中的工作情况：工作温度默认为室温；对压环、药筒和弹丸采用固定约束；对橡胶环套1、橡胶环套2 采用X方向上的位移约束。在加载载荷时，考虑到非线性材料易产生大变形的特点，因此需要设置载荷步和载荷子步以增强求解结果的收敛性［10］，对橡胶环套1 的凸出部分施加大小（文章选取1 470 kN）的水平载荷，按此条件进行模拟。

1.4 仿真结果与分析

应用ANSYS Workbench 对表1 中的五种不同材料的橡胶环进行了仿真。模拟软收口过程中橡胶环的von-mises 应力、橡胶环的应变以及药筒的位移进行了具体分析，发现聚氨酯橡胶环在发生较小应变时，可使药筒产生较为宏观的变形，而其他四种橡胶环则在发生较大形变时，因施加的载荷过大，产生了求解不收敛的情况，故对除聚氨酯橡胶环之外的其他四种橡胶环由1 470 kN 的力载荷均改为9 mm 的位移载荷以观察其形变情况。得到的不同材料橡胶环的vonmises 应力云图如图5 所示。

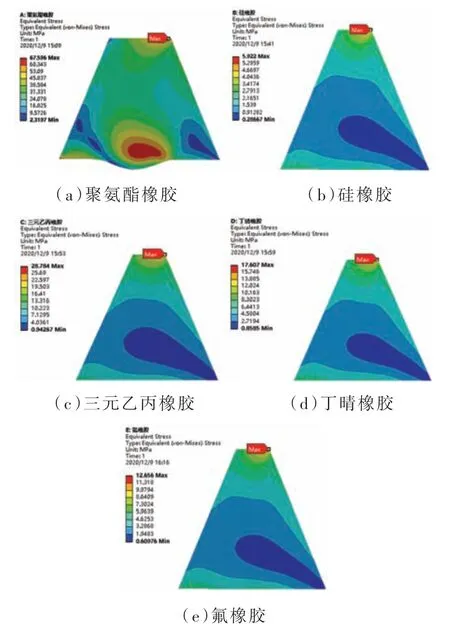
图5 不同材料橡胶环的von-mises 应力云图

图5 为不同材料的橡胶环von-mises 应力云图，由图可以看出聚氨酯橡胶环在产生较小应变的同时其产生的最大von-mises应力不超过68 MPa，小于其最大抗压强度（160～1 000 MPa），因此选用聚氨酯橡胶环在此工况中是安全的。得到的不同材料的橡胶环应变分布云图如图6 所示。

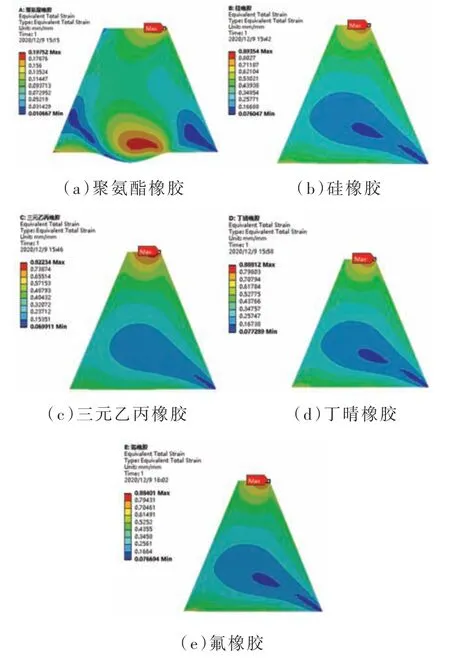
图6 不同材料的橡胶环应变分布云图

图6 为不同材料的橡胶环在收口结合时产生的应变分布云图，由图6 可以看出除聚氨酯橡胶环之外的其他四种材料的橡胶环均在9 mm 的位移载荷之下产生了超过80%的应变。此时和橡胶环套、压环、药筒以及弹丸的配合关系（以三元乙丙橡胶为例）如图7 所示。

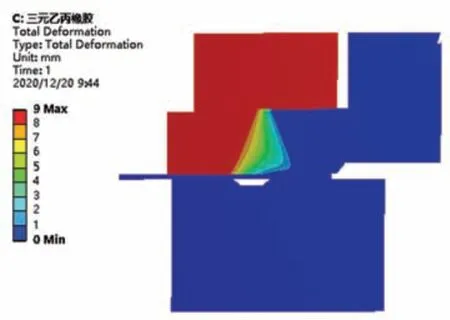
图7 三元乙丙橡胶环9 mm 位移载荷下位移图

由图7 不难发现，在施加9 mm 位移载荷的工况之下，此时的橡胶环已经被环套挤压至错过收口的最佳位置，无法完成收口作业。药筒被不同材料橡胶环挤压产生的位移云图如图8所示。

图8 药筒被不同材料橡胶环挤压产生的位移云图

由图8 可以较直观的反映出不同材料橡胶环对于药筒的收口结合情况，力载荷作用在聚氨酯橡胶环上时，聚氨酯橡胶环发生形变使得药筒产生较为明朗的变形，相较于聚氨酯橡胶环，其他材料的橡胶环直至被环套挤压至错过收口的最佳位置时，对药筒收口效果仍非常细微。综上所述，以上五种材料的橡胶环，应选择聚氨酯橡胶环来完成此工况的柔性结合作业。

2 聚氨酯橡胶环选材（硬度）复核分析

邵氏95 A 的聚氨酯橡胶，在压缩量较小的情况下（e≤5%）弹性模量远大于其他硬度的橡胶，有一定的弹性，且耐冲击强度较高，然而这种硬度的橡胶受压缩时可能引起永久变形与松弛现象［11］，而本收口装置中的橡胶环考虑到更换较为困难、收口作业的重复性以及经济成本等因素，因此需要考虑邵氏硬度较低的橡胶环，其相较于邵氏95 A 具有较好的流动性，且不易发生永久变形，可以完成重复作业，适合该软收口装置的工况。

此处考虑邵氏80 A 与邵氏70 A 硬度的聚氨酯橡胶环，材料模型仍然采用二参数Mooney-Rivlin 模型进行数据拟合得到，然后对其进行静力学分析，不同邵氏硬度的聚氨酯橡胶环材料参数汇总如表2 所示。

表2 不同邵氏硬度聚氨酯橡胶环材料参数汇总

对邵氏80 A 硬度的聚氨酯橡胶圈采用和邵氏95 A 硬度聚氨酯橡胶环相同的边界条件和1 470 kN 液压载荷，观察此工况下药筒的变形情况，所得到的邵氏80 A 硬度的聚氨酯橡胶环挤压药筒产生的位移云图如图9 所示。

图9 80 A 硬度橡胶环9 mm 位移载荷下位移云图

由图9 可发现，当施加1 470 kN 油压载荷时，药筒在邵氏80 A 硬度聚氨酯橡胶环的作用下，产生了较宏观的径向形变，具体的压力值可通过液压系统的无级调节以满足火工品的产品要求，因此该硬度的聚氨酯橡胶环仍可满足柔性结合作业需求。邵氏70 A 硬度的聚氨酯橡胶环在9 mm 位移载荷下产生的位移云图如图10所示。

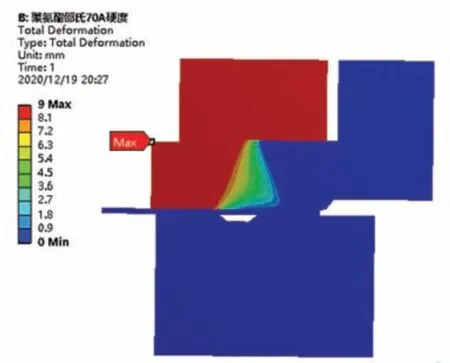
图10 70 A 硬度橡胶环9 mm 位移载荷下位移云图

由图10 不难发现，此时的橡胶环已被环套挤压至错过收口的最佳位置，虽也使得药筒发生了一定的变形，但是仍无法完成收口作业的要求。综上所述，聚氨酯橡胶环应该选择邵氏80 A 硬度较为合适。

3 油压压力与火工品分解力关系研究

在火工品软收口装置柔性结合研究的背景下，结合之后火工品的可靠性也是极其重要的一面。在本工况中，当收口油压不足或收口高压阀未打开时，可引起收口处药筒变形过小，此时火工品药筒和弹丸的分解力（即变形后药筒和弹丸的轴向摩擦力）低于标准，在火工品使用时，会导致药筒和弹丸提前剥离，无法完成正常的爆炸效果；当收口油压过高时，可引起收口处药筒径向形变过大，此时火工品药筒和弹丸的分解力（即变形后药筒和弹丸的轴向摩擦力）高于标准值，在火工品使用时，会导致药筒和弹丸无法分离，导致炸膛等严重后果。故需要研究油压压力、橡胶环压力以及火工品分解力之间的相关性，以确保火工品的正确作业。

首先，使用拉力试验机测定收口完成并已能正常使用火工品批次的分解力，此批火工品的工况：液压驱动力F为1 470 kN。此时需通过已知工况油压和药筒的径向位移、橡胶环的轴向压缩位移计算出橡胶环的支反力。首先通过Workbench 表示出聚氨酯橡胶环的支反力FRa，支反力（与橡胶环对药筒的压力大小相同，方向相反）如图11 所示，然后对支反力进行理论推导，以求得橡胶环对药筒的压力，如式（3）～（8）所示［12］。

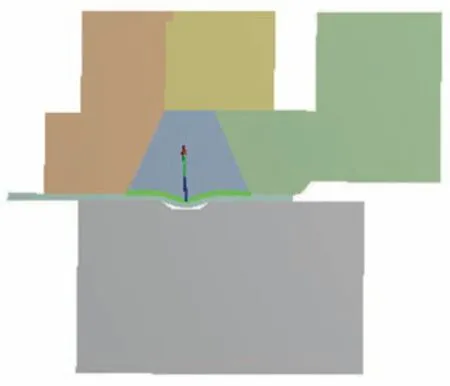
图11 液压缸油压1 470 kN 时药筒对橡胶环的支反力

位移的边界条件BC（u）主要有两种类型，即零位移边界条件和给定具体数值的位移边界条件，此工况下，药筒的位移以及橡胶环的位移均已知，显然是给定数值的位移边界条件。

设所建立的整体刚度方程（将其进行分块）为：

式中，Kij为已知的刚度系数；为已知的位移；为已知施加的力载荷列阵；Fa、为未知的力载荷矩阵；qb为未知的位移；FRa为待求的支反力列阵。

此处采用直接法求解未知的位移，对于边界条件，将方程（4）写成两组方程：

在求得未知位移qb之后，将整体的位移列阵代回原整体刚度方程，计算出力Fa，再由式（5）可推导出橡胶环的支反力FRa，即：

通过ANSYS Workbench 计算出该工况下药筒对橡胶环的支反力，如图12 所示。

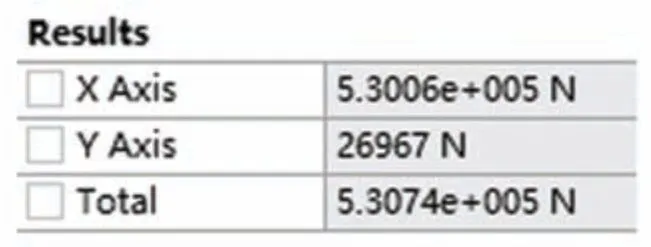
图12 油压1 470 kN 时药筒对橡胶环的支反力计算结果

通过计算，得到其支反力合力FRa约为530 kN，即橡胶环对药筒的压力合力为530 kN。使用拉力试验机对该批次火工品（液压驱动力为1 470 kN）进行拉力试验，测得的数据如图13 所示。

图13 拉力试验机火工品分解力试验

由拉力试验机测得该火工品分解力为19.1 kN，而根据火工品使用标准可得知，当火工品分解力介于18.5～20.0 kN 时，火工品均可正常使用。依次将对一批量火工品进行不同油压压力以及火工品分解力试验，并通过式（3）～（8）计算出对应火工品的橡胶环压力F1，为了增强工况下油压压力的适用性，将液压驱动力F转换为液压油压力p，转换公式如下：

式中，p液压油压力；F为液压驱动力；S为无杆活塞与液压油接触面积。

其油压压力p、橡胶环压力F1以及火工品分解力F2如表3 所示，将火工品分解力F2与油压压力p、火工品分解力F2与橡胶环压力F1做成折线图，如图13 所示。

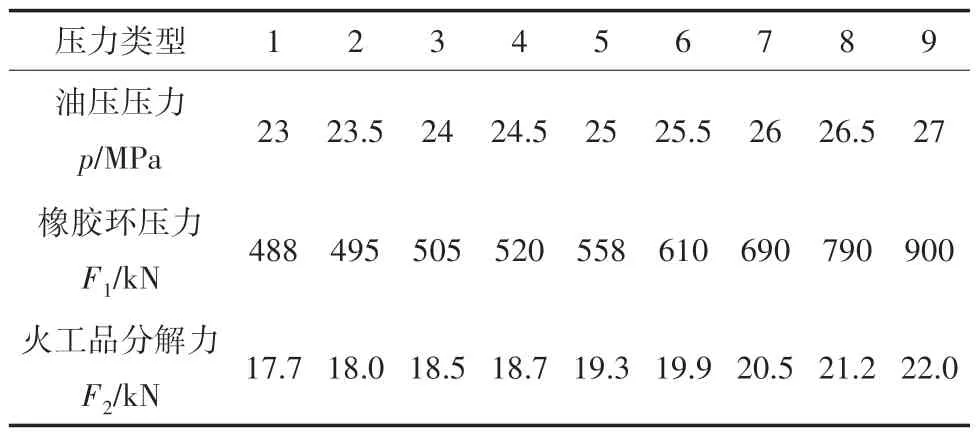
表3 油压压力、橡胶环压力以及火工品分解力测试数据汇总

由图14 易知，火工品分解力随着油压压力的增大而升高，且升高的趋势总体由慢变快；火工品分解力随着橡胶环压力的增大而升高，但其升高的趋势总体由快变慢。橡胶环由火工品使用标准可得出，当火工品分解力F2介于18.5～20.0 kN 时，均可以完成火工品正常的使用，由表3 和图13 可知，当油压压力p介于24～25.5 MPa、橡胶环压力F1介于505～610 kN 时，所得到火工品的可靠性是符合标准的。