基于变量选择比自适应迭代法的近红外光谱变量选择方法研究

文鹏，宦克为，赵环，王迪

（1.长春理工大学 物理学院，长春 130022；2.中移建设有限公司吉林分公司，长春 130112）

近红外光谱是指波长介于可见光与中红外光之间的电磁波，波长范围为780～2 500 nm 之间，主要包含有C-H、N-H、O-H 等含氢基团在近红外谱区吸收的倍频及合频［1］。近红外光谱分析技术具有无损、高效、成本低、范围广等诸多优势［2］，在工农、医药、食品等领域被广泛应用［3］。但由于近红外光谱存在信号弱、谱带宽、重叠严重等问题［4］，并不是所有变量都与需要检测的成分相关联。为了简化模型，提高模型预测精度［5］，变量选择成为近红外光谱分析（Near Infrared Spectroscopy，NIRS）的关键环节。常用的变量选择方法包括无信息变量消除法（Uninformative Variable Elimination，UVE）［6］、蒙特卡洛无信息变量消除法（Monte Carlo-Uninformative Variable Elimination，MCUVE）［7］、遗传算法（Genetic Algorithm，GA）［8］等。近年来，吴海龙等人［9］提出了基于模型集群分析［10］（Modelpopulation Analysis，MPA）思想的变量选择方法，如竞争自适应重加权采样法（Competitive Adaptive Reweighted Samplingmethod，CARS）［11］、自助软收缩法（Bootstrapping Soft Shrinkage，BOSS）［12］、随机蛙跳法（Random-Frog，RF）［13］、迭代保留信息变量法（Iteratively Retains Informative Variable，IRIV）［14］、变量组合集群分析法（Variable Combination Population Analysis，VCPA）［15］以及稳定自助软收缩法（Self-Bootstrapping Soft Shrinkage，SBOSS）［16］等。上述变量选择方法一定程度上简化了近红外光谱预测模型，但仍存在模型过拟合、预测精度低、鲁棒性差等问题。

基于MPA 思想提出了一种新的变量选择方法——变量选择比自适应迭代法（Variable Proportional Selection Adaptive Iteration，VPSAI）。通过蒙特卡洛采样（Monte Carlo Sampling，MCS）从样本中采集多组互不相同的样本子集，利用偏最小二乘法（Partial Least Squares，PLS）计算出不同子集不同的回归模型以及求出每个变量回归系数的平均值和标准差，进而求出每个变量的贡献值，得到每个变量的初始权重，将初始权重与加权自助采样法（Weighted Bootstrap Sampling，WBS）相集合，对变量空间进行迭代得到多组不同子集，用PLS 进一步建立每组子集回归模型，同时计算出每组子集交互验证均方根误差（Root Mean Square Error of Cross Validation，RMSECV），将RMSECV 较小的回归模型保留下来，上述过程反复迭代，最终选取RMSECV 最小的变量集合作为最佳特征变量［18］。

1 实验及原理

1.1 数据来源

1.1.1 小麦数据集

小麦近红外光谱数据集来源于网址https：//eigenvector.com/resources/data-sets/［19］。包含231 个小麦样本，它的波长范围为1 104～2 495 nm，波长间隔为12 nm，一共有117 个波长点，小麦蛋白质含量均用化学方法测量所得到，图1 为小麦的近红外光谱图。使用Kennard-Stone（K-S）算法将样本集进行分类，选取153 个样本作为校正集，78 个样本作为预测集，小麦蛋白质含量分布如表1 所示［20］。

表1 校正集以及预测集中成分含量统计数据分布

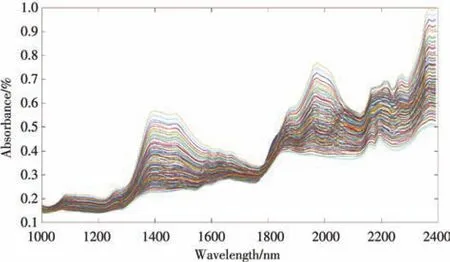
图1 小麦的近红外光谱图

1.1.2 牛奶数据集

牛奶近红外光谱数据集来源于文献［17］。包含67个牛奶样本，近红外光谱波长范围为1 000～2 510 nm，一共有1 557 个光谱点，扫描间隔为0.97 nm，牛奶样本的蛋白质含量用化学方法测量得到。图2 为牛奶的近红外光谱图。使用K-S算法将牛奶样本集进行分类，43 个样本作为校正集，24 个样本作为预测集，牛奶中蛋白质含量如表1 所示。

图2 牛奶的近红外光谱图

1.2 原理方法

1.2.1 光谱预处理

PSAI 使用的光谱预处理方法为均值中心法，与其做对比的几种变量选择方法（BOSS、UVE 以及CARS）也使用相同的方法，这样就能在相同光谱预处理条件下突出PSAI 变量选择方法的优越性，均值中心法常被用于增加样品光谱之间的差异，有助于提高预测模型的稳健性和预测能力。

计算校正集样本的平均光谱：

式中，n为校正样品数；P=1，2，3，…，m，为波长点；X（1×m）为对未知的样品光谱。

1.2.2 PSAI 算法原理

PSAI 算法步骤如下：

（1）运用K-S 算法把样本集分为校正集和预测集。

为维护欧盟内部金融稳定，确保在银行业危机时期，有效地清算处置金融机构，欧盟成立风险处置委员会，设立专项风险处置基金，用于问题银行的风险处置，各国层面的存款保险制度实际上只起到了付款箱的作用。其他国家也存在设立金融机构风险处置基金和存款保险基金的做法。如，德国2010年设立专项基金，专门用于问题银行的风险处置，包括提供过桥贷款、进行股权收购等。

（2）运用MCS 随机从校正集中选取60%的样本作为样本子集，采样N1次得到N1组不同的样本子集。

（3）运用PLS 建立出N1个样本子集的回归模型，进而求出不同样本子集中相同变量的回归系数的均值和标准差，再计算出每个光谱变量的贡献值，设置初始权重，计算方法如下：

式中，Uj为第j个变量回归系数的均值；bi，j为第j个变量在第i个回归模型中的回归系数；N为蒙特卡洛的采样次数；SDj为第j个变量的标准差；Sj为第j个变量的贡献值；Wj为第j个变量的初始权重。

（4）设置迭代结束条件。

（5）根据每个变量的初始权重Wi结合WBS对整个变量空间进行P次采样，得到P组变量子集，运用PLS 建立每组变量组合的预测模型，记录每个变量在每组变量子集中的回归系数bi，j和每个回归模型的RMSECV，保留RMSECV 最小的变量子集作为最佳变量子集。

（6）计算每个变量在不同变量子集中的bi，j，并根据公式（3）～（6）计算出新的Wj。

（7）统计出在迭代过程中保留的全部最优变量子集，直到变量的数量达到1 时终止，并且挑选其中RMSECV 值最小的变量子集作为最终的选择结果，并根据PLS 建立预测模型。

1.3 模型评价

本研究采用的模型评价参数分别是建模均方根误差（RMSEC）和预测均方根误差（RMSEP）。

公式如下：

1.4 控制参数

由表2 所示，通过对PSAI 设置相同控制参数对小麦和牛奶的样本集进行变量选择。通过反复实验得到最优参数设置。

表2 PSAI 控制参数

2 实验结果讨论

2.1 基于PSAI 的近红外光谱变量选择

利用PSAI 对牛奶和小麦的近红外光谱进行变量选择。利用MCS 重复一万次对近红外光谱数据集的原有样本空间进行随机采样，就可以得到一万组互有区别的样本子集，运用PLS 建立每个样本子集的回归模型，根据公式（3）～（6）计算出不同样本子集相同变量的回归系数的均值和标准差以及贡献值，最终给出初始权重Wj；根据每个变量的初始权重Wj结合WBS 对整个变量空间进行1 000 次采样，得到1 000 组变量子集，运用PLS 建立变量子集的预测模型，得到每个变量在变量子集中的回归系数bi，j，以及每个回归模型的RMSECV，保留RMSECV 最小的变量子集作为最佳变量子集；上述过程反复迭代100 次，RMSECV 最小的变量子集为最佳特征变量。

2.2 牛奶数据集的变量选择结果分析

PSAI 方法运行20 次，不同变量的选择频率如图3 所示。选择的特征变量主要有1 088 nm 与仲胺二倍频区相对应；1 138～1 163 nm 与C-H 三倍频区相对应；1 765～1 850 nm 与SN、CH3、CH2伸缩第一倍频区相对应。其中，选择频次在80%～90%之间的变量有1 138 nm、1 139 nm、1 140 nm、1 153 nm；选择频次在90%以上的变量有1 148 nm、1 149 nm、1 787 nm、1 792 nm；选择频次100%的变量有1 775 nm、1 776 nm、1 803 nm，被选择变量与牛奶中蛋白质吸收峰相一致。

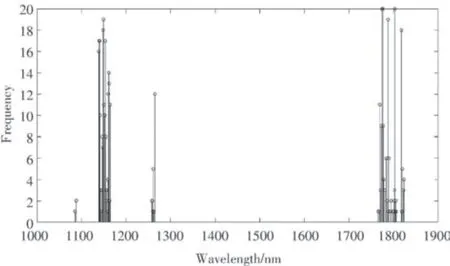
图3 牛奶数据集的不同变量选择频率

2.3 小麦近红外光谱数据集变量选择结果分析

PSAI 方法运行20 次，不同变量的选择频率如图4 所示。选择的特征变量1 116～1 248 nm 与C-H 键二级振动倍频相对应；1 260～1 140 nm 与C-H 组合频以及游离NH 一倍频相对应；1 536～1 644 nm 与氢键键合NH2 倍频相对应；1 944～2 064 nm与游离OH组合频相对应；2 304～2 400 nm与C-H 组合频相对应。其中，选择频次在70%～80%之间的变量有1 956 nm、1 944 nm、1 284 nm、1 272 nm、1 260 nm、1 620 nm；选择频次在80%～90%之间的变量有2 364 nm；选择频次100%的变量有1 140 nm、1 440 nm、2 064 nm，被选择变量与小麦中蛋白质吸收峰相一致。

图4 小麦数据集的不同变量选择频率

2.4 不同建模方法的预测结果分析

由表3 所示，在牛奶数据集上，与CARS-PLS、UVE-PLS、BOSS-PLS 相比，PSAI-PLS 的RMSEC分别由0.078 0、0.128 2、0.106 0 变为0.080 3；RMSEP 由0.068 7、0.110 9、0.083 8 下降到0.062 8，预测精度分别提升了8.7%、43.3%、25%。在小麦数据集上，与UVE-PLS、BOSS-PLS、CARS-PLS相比，RMSEC 由0.596 6、0.698 8、0.632 2 下降到0.552 0；RMSEP 由0.696 1、0.849 5、0.776 5 下降到0.667 8，预测精度提升了4.1%、21.4%，14%。

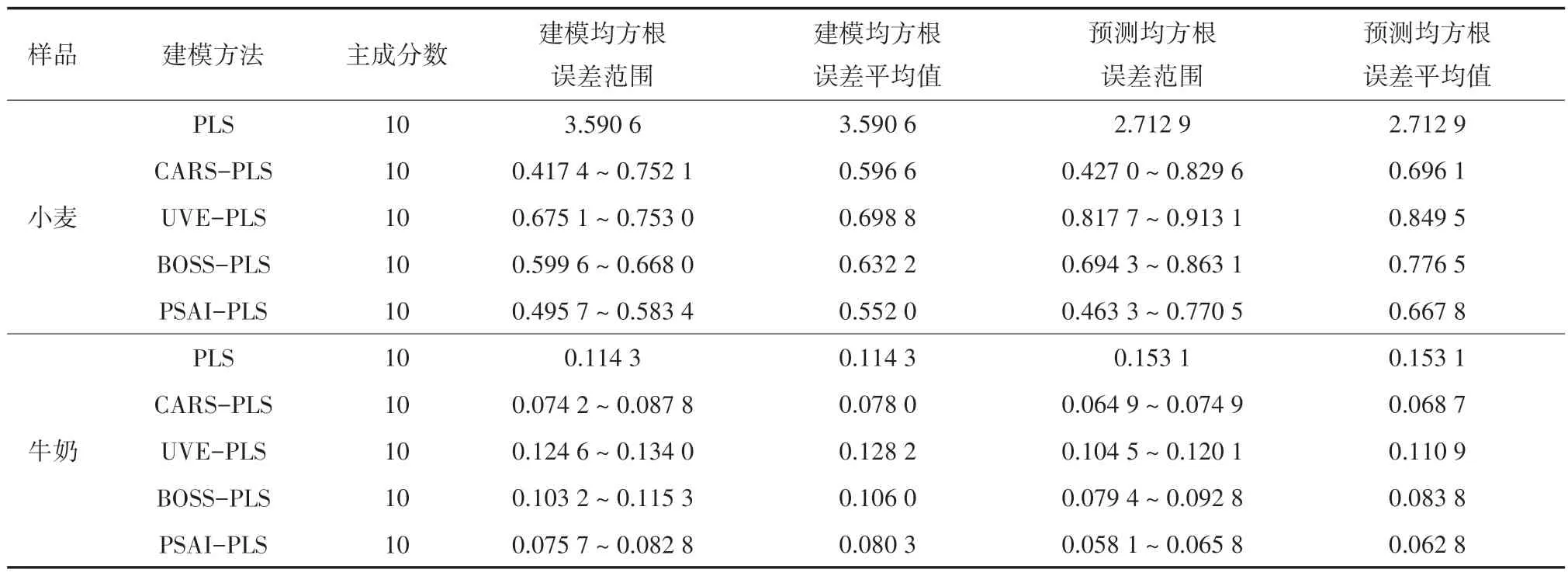
表3 不同建模方法统计结果

综上，PSAI 能够很好地弥补样本采样局限性以及人为设置初始权重的主观性，可以有效消除变量空间中的无信息变量和干扰变量，极大程度的简化模型，提高建模预测精度。

3 结论

基于MPA 思想PSAI 通过提高MCS 采样次数以及利用变量回归系数的均值与变量的标准差来设定权重，在反复迭代中选取最佳变量。这种方法弥补了单一使用MCS 的不足，改善了BOSS 方法在设置权重方面的不足，突出了PASI变量选择方法的优越性。在公开的牛奶和小麦近红外光谱数据集上，PASI-PLS 与BOSS-PLS、CARS-PLS、UVE-PLS 模型相比较，具备更高的预测精度和鲁棒性，PASI 方法进行变量选择是可行的。