小口径火炮抽壳及药筒再进膛有限元分析

程 斌，王惠源，刘 宾，任冬冬，杨 硕

(1.中北大学 机电工程学院，山西 太原 030051；2.中北大学 信息与通信工程学院，山西 太原 030051)

转管炮发射时，药筒直接受到火药气体的作用，发生塑性变形进行贴膛.在弹丸发射后将药筒抽出，为抽壳过程.抽壳阻力的变化对自动机的设计具有重要意义.实践中发射后的药筒再入弹膛会导致自动机的产生故障.

近年来，很多学者对抽壳进行了计算仿真，高乃同(文献[1-2])通过理论计算了抽壳力，还对高压抽壳进行了数值分析；文献[3]将仿真结果和理论计算进行对比；文献[4]得出抽壳力和抽壳速度随时间变化曲线，分析了抽筒模板位置的变化对抽筒速度的影响；文献[5]建立轴对称模型和三维模型来求解抽壳力，讨论了初始间隙对抽壳力的影响；文献[6]给出抽壳力随时间变化曲线，分析初始间隙、弹膛壁厚以及摩擦系数对抽壳力的影响；文献[7]通过试验比较得出非线性计算的抽壳力较为准确，温度变化对抽壳(钢质药筒)影响不大的结论；文献[8]通过仿真找出药筒的薄弱地方，并对其进行了结构优化.

以上学者对抽壳作了大量的研究计算，但是很少有人针对不同膛压下的抽壳进行研究，对于药筒的回膛，更是鲜有研究.本文对不同膛压下30 mm转管炮的药筒进行抽壳阻力变化和药筒再进膛现象的有限元分析.文中将药筒推入膛内，称之为回壳，药筒回膛的阻力称之为回壳力.

1 模型建立

1.1 材料模型

本文分析的部件包括弹膛、药筒和机头，弹膛采用炮钢材料，建立弹塑性材料模型，药筒的材料分为弹体和弹口两部分.药筒采用双线性材料模型，材料失效阶段采用剪切和拉伸失效.机头为炮钢材料.药筒与弹膛的具体材料参数见表 1.

表 1药筒与弹膛的材料参数

1.2 有限元模型

用UG对弹膛，药筒以及机头进行三维建模，如图 1 所示，药筒与弹膛的配合及尺寸如图 2 所示，图中，药筒体部与弹膛的间隙为0.24 mm，药筒口部与弹膛的间隙为0.43 mm.药筒、弹膛及机头全部采用六面体网格[9]，单元类型为C3D8R，为了避免沙漏效应，药筒采用4层网格，弹膛及机头的网格则较大一些，其网格模型如图 3 所示.

图 1弹膛、药筒以及机头的三维模型Fig.1 Three-dimensional models of chamber, cartridges and bolt

图 2药筒与弹膛的配合Fig.2 Coordination of cartridge and chamber

图 3弹膛、药筒以及机头的网格Fig.3 Mesh for chamber ,cartridges, and bolt

1.3 仿真过程

分三个阶段对药筒抽壳以及回壳进行分析：(1) 将弹膛外表面轴向约束，药筒内加载膛压，压力曲线如图 4 实线所示，将机头后端面轴向位移约束；(2) 在膛压降到某一值时，取消机头后端约束，将其以图 5 所示的速度抽出；(3) 当机头抽出一段距离后，将其以相反的速度推入弹膛，以此来模拟回壳.

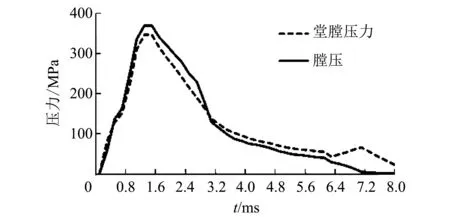
图 4膛压及壳膛压力随时间变化曲线Fig.4 Variation curve of chamber pressure and shell chamber pressure with time

图 5抽壳速度Fig.5 Extraction velocity

1.4 实验分析

用CT技术对发射过的药筒进行扫描，如图 6 所示，测量其尺寸.选取五个截面对仿真结果与实验数据进行比较，选取的截面位置如图 7 所示，比较结果见表 2，第三行的误差为(仿真值-实验值)/实验值，通过比较二者结果，药筒口部(截面5)误差最大为1.9%，小于5%，所以此次仿真的结果是可信的.

图 6击发后药筒的CT摄影Fig.6 CT photography of cartridge after firing

图 7选取药筒不同截面的位置Fig.7 Selecting the positions of different sections of the cartridge

截面1截面2截面3截面4截面5仿真/mm40.239.538.738.032.3实验/mm39.839.238.537.631.7误差/%1.00.80.51.01.9

2 结果分析

2.1 加载阶段的药筒与弹膛的受力分析

首先分析火药气体加载阶段的药筒受力，药筒变形分为自由膨胀,贴膛后与身管共同膨胀，以及膛压下降时与身管共同收缩三个阶段.其中自由膨胀又分为两个阶段：药筒的弹性变形和药筒的塑性变形.在药筒径向变形的同时，药筒伸长并向后退，但很快越过弹底间隙被机头挡住.当药筒的膨胀量超过初始间隙时，药筒接触弹膛(贴膛)，当膛压从最大值开始下降后，药筒与弹膛共同收缩，根据仿真结果分析，在最大膛压时，弹膛所受的压力为340 MPa，而弹膛材料为炮管材料，其屈服应力在1 000 MPa以上，所以弹膛为弹性收缩.药筒开始是弹性收缩，之后的塑性变形则不可恢复.

提取弹膛内壁的压力如图4虚线所示，此压力即为壳膛压力，壳膛压力与膛压的数值相近，最大膛压时，壳膛压力与膛压的相差值最大，差值为40 MPa，弹膛收缩时，由于弹膛和药筒之间有接触，所以壳膛压力逐渐超过了膛压值，说明此时弹膛的收缩量要大于药筒的收缩量，超过6 ms 时，壳膛压力增大，则此时弹膛与药筒之间的相互作用力增大，药筒的弹性形变已经恢复，而弹膛的弹性还在恢复，则药筒被弹膛挤压，药筒发生反向的弹性变形，此时药筒的弹性变形会对后续的抽壳力产生影响.在8 ms时，膛压降为0 MPa，而壳膛压力为17 MPa，结合图 8 所示，在8 ms时，弹膛的应变为7.14×10-5mm，所以在膛压降为0 MPa时，弹膛的弹性形变仍然没有恢复，弹膛的弹性恢复的力也会对后续抽壳产生影响.

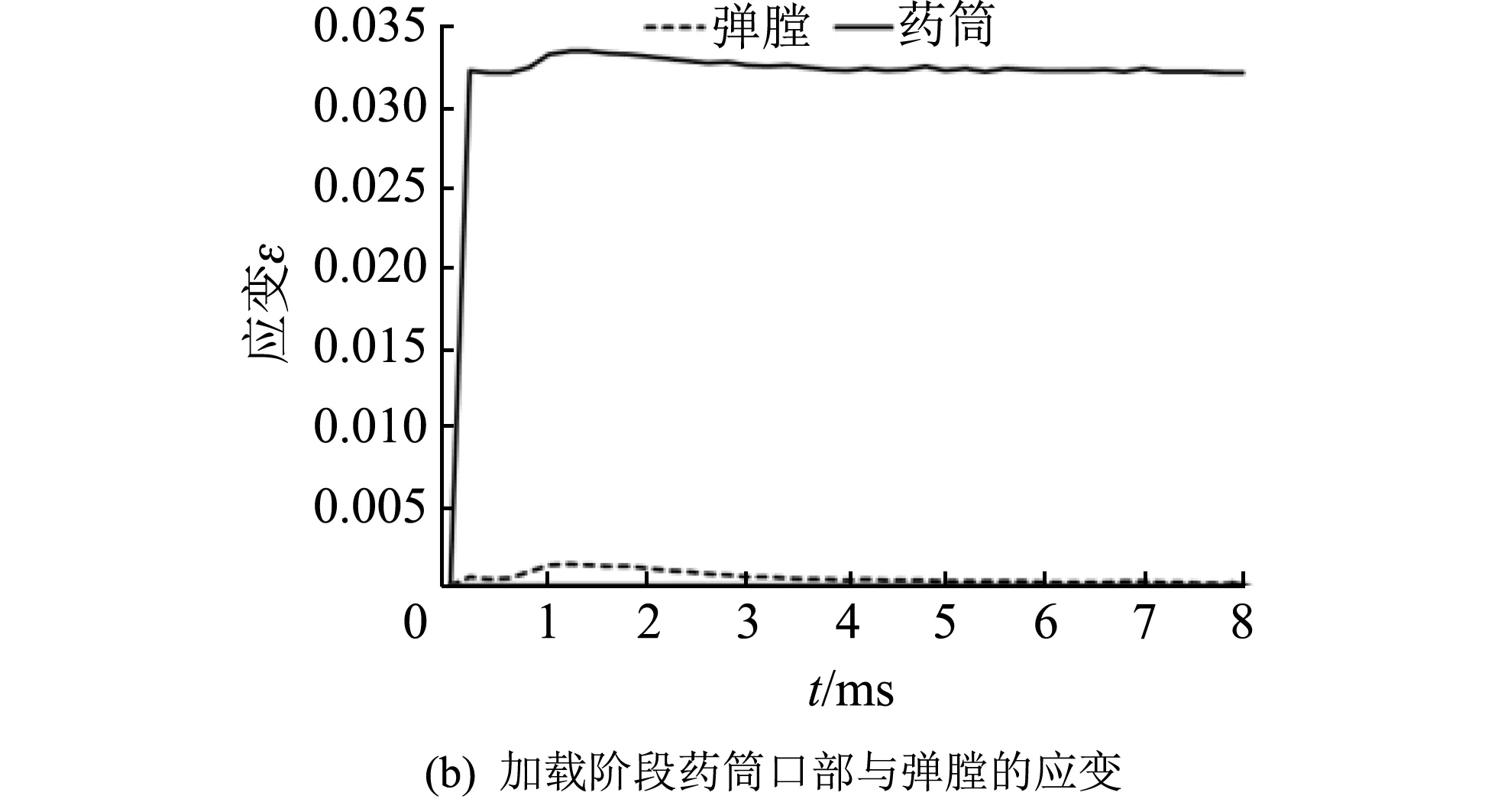
图 8加载阶段药筒与弹膛的应变Fig.8 Strain of cartridge and chamber in loading stage

药筒与弹膛随时间变化的应变曲线如图 8 所示，在膛压卸载完毕时，药筒的弹性形变恢复，塑性变形则不可恢复，而且由于药筒口部的强度极限小于药筒体部，所以药筒口部的塑性形变要大于药筒体部，而弹膛发生的是弹性应变，所以弹膛的应变和药筒相比要小得多.

在膛压加载阶段，机头的变形也是不可忽略的，当药筒贴上机头之后，机头开始发生弹性变形，机头的屈服应力也大于350 MPa，所以在加载阶段，机头也只发生弹性变形，且机头压力与图4壳膛压力类似，由于机头与药筒之间存在缝隙，所以药筒在膛内有轴向位移，药筒位移如图 9 所示，负方向为与炮口相反的方向，如图所示，加载膛压时，药筒迅速后退贴紧机头，且将机头进行弹性压缩，在膛压最大时，药筒后退的位移最大，之后随着膛压的下降，机头的弹性变形开始恢复，从而推动药筒往炮口方向运动，在8 ms时，药筒的瞬时速度为23 m/s，由于药筒的速度方向为炮口方向，所以此时药筒所受的摩擦力指向炮尾方向.这个摩擦力为接下来的抽壳提供了动力.

图 9药筒轴向位移Fig.9 Cartridge axial displacement

图 10药筒不贴膛位置Fig.10 Cartridge not affixed to the chamber position

药筒在膛压作用下开始贴膛时，药筒根部有一段不贴膛处，如图 10 所示，随着膛压的增大，不贴膛的长度逐渐减小，最终接近消失，在这个过程中，药筒未贴膛段类似于悬臂梁，药筒根部受到弯矩作用，图 10 所示应力最大的两处最终材料受损，为后期的药筒进膛埋下隐患.

2.2 抽壳过程及抽壳力分析

在膛压降到0 MPa时，机头开始拉动药筒后退，即抽壳过程开始，抽壳的瞬间，随着药筒的抽出，弹膛的弹性变形恢复，药筒被压缩的反向弹性变形也开始恢复，此时弹膛以及药筒的弹性恢复会推着药筒后退，且在抽壳的一瞬间，由于之前的机头作用，药筒有向炮口方向运动的趋势，所以药筒所受的摩擦力指向炮尾，也成为这一瞬间的抽壳推力，这三者的作用力如图 11 所示，Ff为摩擦力，Fd为弹膛的弹性力，Fy为药筒的弹性力，即在抽壳初始，抽壳力为推力，抽壳推力作用的时间很短，之后药筒开始往外抽，弹膛和药筒弹性开始恢复，由弹性应变产生的推力减小，而摩擦力则与运动方向相反，成为运动的阻力.抽壳瞬间的抽壳推力为(负值为推力)

Fz=-(Ffcosθ+Fdsinθ+Fysinθ).

(1)

图 11膛压作用结束后起始抽壳时药筒受力Fig.11 Force of cartridge during initial extraction after the end of the chamber pressure

当抽壳时膛压未降为0 MPa时，作用在药筒底部的压力会推着药筒往外推，火药气体压力对弹壳口部端面的作用力也会推着药筒往外走，而作用在药筒四周的压力则使药筒紧紧挤压弹膛，增大抽壳的摩擦力[10]，且作用在药筒肩部的轴向分力也会对抽壳形成阻力，设膛底的作用力为Fp，火药气体对药筒肩部作用力的为Fp1，火药气体对药筒口部的作用力为Fp2，则起始的抽壳推力为

Fz=Fp1sinθ-Ffcosθ-Fdsinθ-

Fysinθ-Fp-Fp2.

(2)

经过短暂抽壳后，抽壳力变为阻力，此时的抽壳力如式(3)所示，膛压降为0时，Fp,Fp1,Fp2三个作用力消失，抽壳力如式(4)所示.

Fz=Ffcosθ-Fdsinθ-Fysinθ-Fp+

Fp1sinθ-Fp2,

(3)

Fz=Ffcosθ-Fdsinθ-Fysinθ.

(4)

为了验证在抽壳瞬时，抽壳力为推力，进行以下仿真，分两步来进行：(1) 加载膛压，与之前相同，在药筒内壁加载膛压，固定机头后端面，模拟火药发射；(2) 在膛压降为0 MPa时，去掉机头与药筒之间的约束，只保留药筒与弹膛的相互作用，观察药筒的位移.若初始药筒受到推力，则药筒在加载结束时，药筒在推力的作用下会后退.药筒的位移如图 9 所示，0～8 ms之间为加载阶段，在8 ms之后，药筒将不再受外力作用，而图示药筒开始往负方向(抽壳方向)移动，由此可得，药筒在初始抽壳时的确受到推力.药筒抽出时的应力应变如图 12 所示，药筒没有发生大的形变，结构完好.

图 12药筒抽出时的应力应变Fig.12 Stress and strain of cartridge extraction

2.3 不同压力下抽壳对抽壳力的影响

本文弹底与拉壳钩之间的缝隙为0.25 mm，不同压力下的抽壳力如图 13 所示，在低膛压时抽壳，加载膛压的时间长，所以抽壳的起始时间靠后，图中抽壳时间越晚，则其抽壳时的膛压越低，图 13 中从右往左依次为膛压在0，10，20，30，40，50 MPa的抽壳过程，抽壳力正值表示抽壳的推力，负值为抽壳阻力.

图 13不同膛压下的抽壳力Fig.13 Extraction force under different chamber pressure

在起始抽壳时，药筒所受的力为推力，且随着抽壳时膛压的增大，抽壳的推力也在增大，不过抽壳推力作用的时间很短暂，时间约为0.35 ms.之后抽壳变为阻力，抽壳的整个时间为5 ms，由图13可知在膛压为50 MPa时抽壳阻力最大，不同膛压下最大抽壳力的数值如表 3 所示，由此可见，随着抽壳时膛压的增大，抽壳力也变大，在10～40 MPa之间，抽壳力的变化比较平缓，这是由于壳膛力在此时发生变化，壳膛力的变化如图 4 所示，在膛压降为50 MPa抽壳时，壳膛之间的压力比较大，所以抽壳力就变得很大.

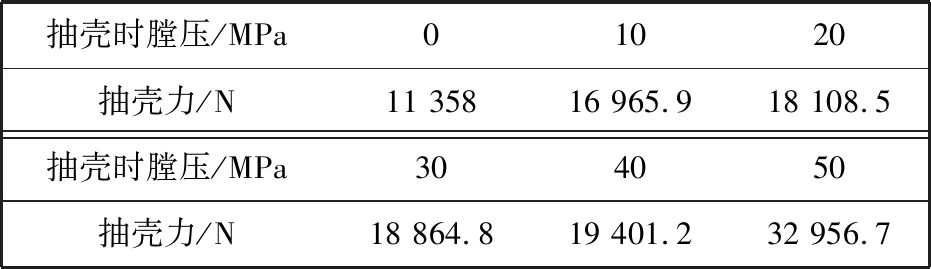
表 3不同膛压下抽壳时的最大抽壳力

2.4 回壳分析

将发射过的药筒推入弹膛的过程，即回壳.

图 14药筒再进膛的变形情况Fig.14 Deformation of cartridge reentry

由上可知，药筒在贴膛时药筒根部两处材料受损，所以在回壳时，当药筒接触弹膛时，推弹阻力使药筒薄弱处发生变形产生凸起，药筒的变形如图 14(a) 所示，与图 10 所受的应力最大处吻合，药筒产生两个凸起，这两个凸起均为药筒受膛压时的最大受力处，凸起的最大尺寸分别为42.14 mm 和42.15 mm，药筒凸起的尺寸要大于弹膛尺寸，之后药筒在推弹力的作用下继续前进，当药筒发生变形产生凸起的部分接触到弹膛时，在推弹力的作用下，如图 14(b) 所示，药筒凸起部表面材料发生断裂，而推弹阻力也变得很大，本文强行将药筒推入弹膛，结果如图 14(c) 所示，药筒根部完全破坏，由此可知，将击发后的药筒再次完全进入弹膛是不现实的.

3 结 论

1) 药筒在加载膛压时发生塑性变形，弹膛只有弹性形变，药筒根部由于贴膛滞后造成材料受损，药筒在加载阶段的膛内运动会影响后续的抽壳力.

2) 在抽壳的一瞬间，药筒受到的抽壳力为推力，推力作用的时间约为0.35 ms，且抽壳推力随着抽壳时膛压的增大而增大，之后随着药筒的抽出，抽壳力变为阻力，抽壳阻力也是随着抽壳时膛压的增大而增大，当抽壳时的膛压增大到50 MPa 时，抽壳阻力将达到32 956.7 N.因此，转管武器的发火时间会对抽壳产生较大影响，所以应当合理控制开锁抽壳的时机.

3) 药筒再次进入弹膛时，药筒接触弹膛开始受力后，药筒根部发生大变形产生凸起，之后继续运动，由于药筒凸起尺寸大于弹膛尺寸，凸起部受力断裂，药筒破坏，因此，击发后的药筒无法再次完全进入弹膛.

4) 下一步将考虑弹丸连续发射时，在温度场的边界条件下的抽壳过程的有限元仿真.