时域流形特征增强在数控机床轴承故障诊断中的应用*

黄日进

(广西英华国际职业学院,广西 钦州 530213)

0 引 言

数控机床轴承是一种常用的易损部件,其在生产制造及应用环节对轴承故障类型的诊断分析均有重要的实际意义和经济价值。轴承的振动信号是由机床设备的加速度计传感器等采集的反映轴承部位运行状态的时间序列,是轴承这一动力学系统的运动轨迹表征。轴承故障类型的诊断关键在于不改变信号刻画的动力学系统特性的情况下,强化不同类型故障信号之间的特征差异,从而提高诊断判别的准确性。

在复杂的生产环境干扰及数控机床各部件的振动调制叠加影响下,轴承故障信号包含着大量的高低频和冲击噪声。传统的故障信号分析方法多以在频域、时频域中展开的方式进行,如能量谱[1]、快速谱峭度[2]等,此类方式存在频谱成分的耦合度高、信号的非平稳特征难以表达、原始信号的变换流程长等不足。而且信号故障类型诊断过程需从多域指标筛选出能反映主要差异的维度,这与流形学习理论关注寻找低维流形在高维空间中相同拓扑的嵌入这一目标高度契合。因此,为提升故障类型信息密度、提高判别分类准确度,引入这一种新的路线。Su等[3]将流形学习应用于信号特征融合,构建了基于线性局部切空间排列算法的特征重建方法,用于故障类型识别。Liu等[4]将振动信号的小波分析分解结果作为高维特征集的尺度指标,经线性局部切空间排列算法约减为区分度更好的低维特征集,提升了故障分类的准确率。然而,现阶段在以多域指标构建高维特征集的研究过程中,存在对专家知识和原始数据特性依赖度高的问题。

笔者针对信号的时域振动形态特征,从故障类型诊断主要关注的差异性信息入手,提出一种基于流形学习理论的特征增强方法。首先,将信号时间序列进行相空间重构,在子相空间的集合中计算信息熵,构建出原始信号在高维特征空间中的表征。然后,通过等距特征映射(Isometric Feature Mapping, ISOMAP)算法,基于保持样本集的流形距离,寻找特征空间中同胚的低维流形,来进行故障类型的分类诊断。最后使用德国帕德博恩大学开放的轴承运行数据集[5]对所提方法的有效性进行验证分析。

1 信号特征增强算法

在存在环境和系统噪声的情况下,轴承振动信号可以看作一个非线性、非平稳动力系统的时域运动轨迹。不同故障类型引起的动力系统变化,会刻画出不同的运动轨迹,即通过研究振动信号的轨迹特征便可建立与故障的联系。

利用相空间重构方法,先将采集信号的时间序列重建至高维相空间内。对于一个给定的长度为N的振动信号时间序列x(t)=[x1,x2,…,xN],其嵌入相点表达为:

Xi=[xi,xi+τ,…,xi+(m-1)τ],i=1,2,…,N-(m-1)τ

(1)

式中:m为子相空间维数,m的值应当保证相点内存在有统计学意义的相对变化;τ为延迟时间,τ>0,对于低频信号或振动轨迹变化慢的信号,可以增大取值或通过自相关函数法[6]来定量确定。

对Xi进行原地排序,对排序结果的坐标序列k进行如下变换:

(2)

式中:1是与k等长的全为1的序列;k′刻画了对应子相空间Xi中点的相对变换趋势。此时定义集合K为:

K={k′|i=1,2,…,N-(m-1)τ}

(3)

K中元素的去重数量为m!,计算K的信息熵分量:

E(kl′)=-p(kl′)logp(kl′),l=1,2,…,m!

(4)

式(1)中m的取值若过大,会使子相空间序列均匀化,也增加了运算的复杂度;若过小,则丢失了运动轨迹趋势特征的意义;因此,m取值以3～7为适宜。

以式(4)构造初始振动信号x(t)的特征空间表征x:

x=[E(k1′)E(k2′)…E(km!′)],x∈Rm!

(5)

包含p个信号的样本集D为:

D={x1,x2,…,xp}

(6)

构造集合D内样本的距离矩阵G,其中xij是指样本xi到xj的欧氏距离:

(7)

若样本集包含q类故障,样本数量p可表示为不同类型故障数量之和:

p=p1+p2+…+pq

(8)

根据样本集不同类型故障数量,定义样本的邻域:

(9)

根据邻域δ大小更新距离矩阵G,集合D内每一样本与其他元素前δ小的距离保持为欧式距离,其余更新为+∞。

将更新后的距离矩阵G作为ISOMAP算法[7]输入,可得样本集D在低维特征空间中的同胚流形Z:

Z={z1,z2,…,zp}

(10)

2 数控机床轴承故障诊断

在实际的轴承故障诊断场景中,还需要将经过特征增强的故障类型数据构造的单故障或复合故障进行多类型标签,以训练故障分类器,流程如下:①收集数控机床轴承信号的待测数据及在相同工况下拥有已知故障类型的训练数据;②所有数据以相同子相空间维数m和延迟时间τ的相空间重构法展开;③在展开的子相空间中,计算各部分信息熵,构建m!维特征向量;④以训练数据集在特征空间中的高维流形为基础,通过ISOMAP算法计算同胚的低维流形表达;⑤对训练集数据的低维流形映射以多标签模式标记故障类型,训练分类器;⑥计算待测数据在步骤④中得到的低维流形表示;⑦代入步骤⑤中的故障类型分类器,获得待测数据的故障类型标签。

最终完整的数控机床轴承故障诊断框架示意图,如图1所示。

3 实例数据验证与分析

采用德国帕德博恩大学开放的轴承运行数据集对文中方法进行验证,数据集的采集条件在文献[5]中给出。从该数据集中选取一组健康轴承、三组拥有单一故障的轴承和一组拥有复合故障的轴承振动数据,如表1所列。

表1 实验涉及的数据集故障信息描述表

数据集中除健康轴承外,出现故障的位置包括内圈和外圈,故障类型有疲劳点蚀和塑性形变,每个代码对应的子数据集包含不同工作负载下80个采样信号,采样频率64 kHz,采样时间4 s。以3∶ 2的数量比在每个子集中抽取训练集和测试集,即48个训练信号,32个测试信号,确保两个集合拥有相似的故障类型分布。用一个有序二元组标记故障的位置及类型,其中疲劳点蚀为1,塑性形变为2。

从每个类型的训练信号中抽取一个样本,绘制其0.1 s的时域波形,如图2所示。

图2 五种类型的信号样本时域波形

将训练集信号以延迟时间τ为1,嵌入维数m为3进行相空间重构。计算子相空间的信息熵分量,并在维数为3!=6的特征空间里找到一个表征。相同类型的训练集信号在特征空间中有着邻近的分布。通过ISOMAP算法计算6维特征空间中的低维时域流形,算法的邻域大小定义为每类故障的训练集数量,即为48,最终得到如图3所示的低维分布图。

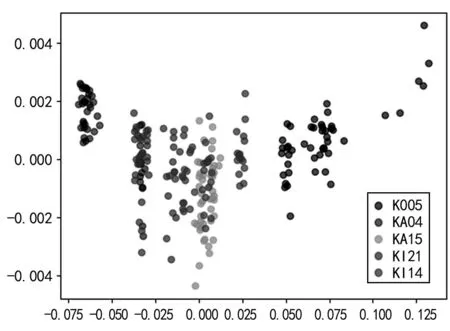
图3 五种类型训练数据的低维流形分布

结合图3展示的分布数据与表1中的标签训练分类器,文中选取了三类工程常用的分类器作为对比:随机森林分类器、决策树分类器和支持向量机分类器。160组测试信号数据经过与训练数据相同的处理后,代入训练完成的故障分类器进行验证,测试结果如表2所列。

表2 三种分类器对测试数据的分类结果 /%

表中复合故障的部分正确识别了外圈或内圈的一种故障,同时另一处被识别为健康;完全正确指准确识别了外圈和内圈的所有故障。实验结果表明,随机森林分类器对文中的轴承故障数据特征强化方法配合度最好,常见分类器对单故障尤其是健康状况轴承的识别有较好的成功率。

4 结 语

将流形学习理论应用于数控机床轴承信号故障诊断领域,提出一种基于ISOMAP的时域流形特征强化方法。轴承振动信号的时域流形刻画了部件的动力学运动轨迹,能反映故障发生带来的系统动力学变化。以时域流形特征为标的能避免在其他域的变换流程过长及信息损失问题。ISOMAP将流形距离作为集合内样本间的距离度量,相同类型的样本在变换过程中被保持在较小的邻域,而异类信号间通过流形距离度量会展现出更大的差异性,契合了信号故障分类诊断所关注的数据特性。

从德国帕德博恩大学轴承故障实验的开放数据集中,选取了包含单一故障和复合故障的五组数据,对文中方法进行验证。验证结果表明,所提方法能够强化数控机床轴承信号的故障类型特征,尤其对健康和故障部件类型数据之间有较明显的区分,对复合故障类型也具有一定的识别能力。