EMVS互质面阵张量波束成形
2024-03-07周成伟史治国
郑 航 周成伟*,2 王 勇 史治国,3
(1.浙江大学信息与电子工程学院,浙江杭州 310027;2.浙江省协同感知与自主无人系统重点实验室,浙江杭州 310015;3.浙江大学国际联合创新中心,浙江海宁 314400)
1 引言
在雷达、遥感、无线通信、射电天文等应用场景中,通过部署传感器阵列对空间信源的波达方向进行精准测算,是实现目标测向、定位、跟踪等诸多功能的基本前提[1-3]。波束成形作为一项基础性阵列信号处理技术,能够对传感器阵列接收信号进行空域滤波形成指向性空间波束,通过波束扫描得到不同方向的空间响应,从而实现信源测向[4-7]。波束成形技术能够有效抵抗干扰且易于部署,已被广泛应用于各类传感器阵列系统中,长期以来发挥着重要作用。随着实际应用场景中对信源测向性能需求的不断提高,现有系统所布设的传感器阵列逐渐演变出新的特点。一方面,为了在系统软硬件资源受限的条件下提升信号感知能力,稀疏化阵元排布的阵列架构开始得到关注[8-11],其中,互质阵列作为一种拥有系统化结构的典型稀疏阵列,能够突破传统均匀阵列信号处理在奈奎斯特采样速率上的限制,在使用相同数量传感器阵元的条件下拥有更大的阵列孔径,从而有效提升波束分辨率[12-17];另一方面,为了满足复杂信源测向场景感知空间极化信息的需求,电磁矢量传感器(electromagnetic vector sensor,EMVS)阵列相比于传统的标量传感器阵列,能够获取入射信号的多极化状态,通过利用更加全面的空间电磁信息与更强的干扰抵抗性,提供更为精准的波束控制与角度估计能力[18-19]。为此,如何发掘互质阵列和EMVS 阵元的独特优势,形成相匹配的波束成形算法设计框架,是当前一个国际前沿研究热点。
为了发挥互质阵列的大孔径优势并降低波束成形器的软硬件复杂度,面向互质线阵的自适应波束成形算法受到广泛关注[20-23]。其中,文献[23]结合互质线阵参数估计与稀疏协方差矩阵重建思想,提出了一种面向互质线阵的鲁棒自适应波束成形算法。为了利用互质阵列波束成形实现信源测向,文献[24]针对互质线阵的阵元稀疏排布特点,从互质线阵稀疏子阵波束谱的分布特性出发,提出了基于乘性准则和最小化功率准则的波束功率合成方法,通过虚峰抑制的波束扫描测算信源波达方向。基于该技术框架,相关研究针对交叉项消除[25]、分辨率增强[26]和水声探测[27]等具体问题及实际应用环境特点提出了相适应的改进方案,促进了互质线阵波束功率合成方法在信源测向上的推广应用。另一方面,为了利用EMVS 阵列的极化域信息,文献[28]提出了一种基于广义旁瓣相消的EMVS 阵列波束成形方法,并证明了该方法相比于传统Capon波束成形算法具有更小的波达方向估计误差。文献[29]考虑极化方向的鲁棒约束,设计能够应对阵元位置失配的EMVS 阵列鲁棒波束成形器,进一步提升了波达方向的估计精度。考虑到互质阵列和EMVS 阵元均能够有效促进波束成形输出性能的提升,融合互质阵元排布特点与EMVS 阵元的EMVS 互质线阵应用研究开始兴起。相关研究工作结合增广虚拟域处理[30-31]与多重信号分类(multiple signal classification,MUSIC)方法,验证了部署EMVS 互质线阵进行信源测向的可行性[32];文献[33]基于EMVS 互质稀疏子阵信号的平行因子分析实现了信源测向的性能提升。为了满足三维空间的信源测向需求,EMVS 互质线阵亟待向EMVS互质面阵演变,以便感知更大范围、更高维度的空间信息。针对互质面阵信源测向需求,基于虚拟域稀疏恢复的方法能够在克服相位模糊的前提下实现二维波达方向估计[34];文献[35]利用一种互质双平行阵列,在虚拟域上应用root-MUSIC方法以完成信源波达方向搜索。然而,这些方法将多快拍接收信号堆叠成矩阵并作后续统计处理。在EMVS互质面阵场景中,由于接收信号涵盖了多维度信息,基于矩阵信号建模与处理的方法将破坏多维接收信号的原始结构,进而影响信源测向的性能。为此,如何设计匹配EMVS互质面阵多维信号结构的空域滤波算法,已成为当前一个亟待解决的研究难点问题。
张量作为一种多维度的数据结构,被用于表征三维及三维以上的数据。丰富的张量分解工具为张量数据的高维特征提取和分析提供了技术支撑[36]。近年来,张量模型被广泛应用于阵列信号处理领域,用于表征多维信号并实现张量化参数估计[37-40]。通过引入张量进行EMVS互质面阵接收信号建模,能够有效保留其所涵盖的复杂空间/时间/电磁特征,并利用张量代数工具,在不破坏信号原始结构的前提下实现高性能的角度信息提取。考虑到张量模型的优越性,面向多维信号的张量波束成形算法成为一个新兴的研究热点。具体而言,文献[41-43]分别提出了面向均匀面阵的最小均方误差(minimum mean square error,MMSE),线性约束最小方差(linear constrained minimum variance,LCMV)以及最小方差无畸变响应(minimum variance distortionless response,MVDR)等传统波束成形设计准则的张量表征方法,并利用张量分解对所设计张量权重优化问题进行求解,验证了对张量信号进行结构化空域滤波的可行性。进一步地,上述张量波束成形算法亦被推广应用于极化敏感阵列及大规模分布式阵列等复杂场景中[44-45]。然而,现有方法仅适用于满足奈奎斯特采样速率的均匀面阵场景,而在EMVS 互质面阵场景下,阵元的稀疏排布将导致模型失配问题,由此引入的虚峰将严重干扰张量波束成形器对信号源波达方向的精准刻画。文献[46-47]提出了面向互质面阵的稀疏张量模型,分别从虚拟域张量信源辨识度优化和非连续虚拟域张量填充的角度,实现了高自由度、高精度的二维波达方向估计。然而,这些方法没有考虑部署EMVS互质面阵。因此,如何匹配EMVS 稀疏阵元排布特点进行虚峰抑制,是利用EMVS 互质面阵张量波束成形进行有效信源测向的关键。
本文提出了一种面向EMVS 互质面阵的张量波束成形算法,实现了基于EMVS 互质面阵接收信号的多维空域滤波与信源精准测向。首先,将构成EMVS 互质面阵的稀疏均匀子面阵接收信号表示为一对涵盖多维度空间电磁信息的张量。在张量信号建模的基础上,构建面向稀疏均匀子面阵张量信号的结构化空域滤波准则,并设计相应的张量化最小方差无畸变响应优化问题。为了有效求解该优化问题,对张量权重进行canonical polyadic分解,将原始张量化最小方差无畸变响应优化问题转换为对应波达方向信息维度与极化状态信息维度的子问题,并根据这些子问题所对应空间维度信息的耦合关系设计交替迭代求解方法,以获得张量权重的全局最优解。进而,基于稀疏均匀子面阵的阵元互质排布特点分析,理论证明各子面阵所对应虚峰的互不重叠特性。从抑制虚峰的角度出发,设计波束功率的互质合成方法,以此构造EMVS 互质面阵张量波束功率图,在波达方向平面上精准刻画信源空间方位。所提算法既能够充分利用EMVS 互质面阵接收信号的多维结构化信息,又能够匹配其阵元稀疏排布特点实现虚峰抵消。仿真结果表明,所提算法具有相较于EMVS 均匀面阵张量波束成形算法更好的信源测向效果。
2 EMVS互质面阵的张量信号建模
如图1 所示,EMVS 互质面阵P 由两个稀疏均匀子面阵P1和P2组成,P1和P2分别包含M1×N1和M2×N2个传感器阵元,且(M1,M2)和(N1,N2)为两对互质整数。稀疏均匀子面阵P1的传感器阵元在x轴和y轴方向上的间隔分别为M2d和N2d,其中d=λ/2 为单位阵元间距,λ表示信号波长。类似地,稀疏均匀子面阵P2的传感器阵元在x轴和y轴方向上的间隔分别为M1d和N1d。由此,P1中第(m1,n1)个传感器阵元在x轴和y轴方向上的位置分别为x1(m1)=(m1-1)M2d和y1(n1)=(n1-1)N2d,其 中m1=1,2,…,M1,n1=1,2,…,N1;P2中第(m2,n2)个传感器阵元在x轴和y轴方向上的位置分别为x2(m2)=(m2-1)M1d和y2(n2)=(n2-1)N1d,其中m2=1,2,…,M2,n2=1,2,…,N2。由于 两个稀疏 均匀子面阵的传感器阵元排布满足互质条件,P1和P2只有在位于原点处的传感器阵元(m1=n1=m2=n2=1)相互重合,而其余传感器阵元在xoy平面内均不重合;因此,EMVS互质面阵P中传感器阵元的数量为M1N1+M2N2-1。同时,与传统标量传感器不同的是,EMVS 互质面阵中各传感器阵元利用三个相互正交的电偶极子和三个相互正交的磁偶极子来实现极化状态的感知,形成六路输出以描述完备的电磁场信息。
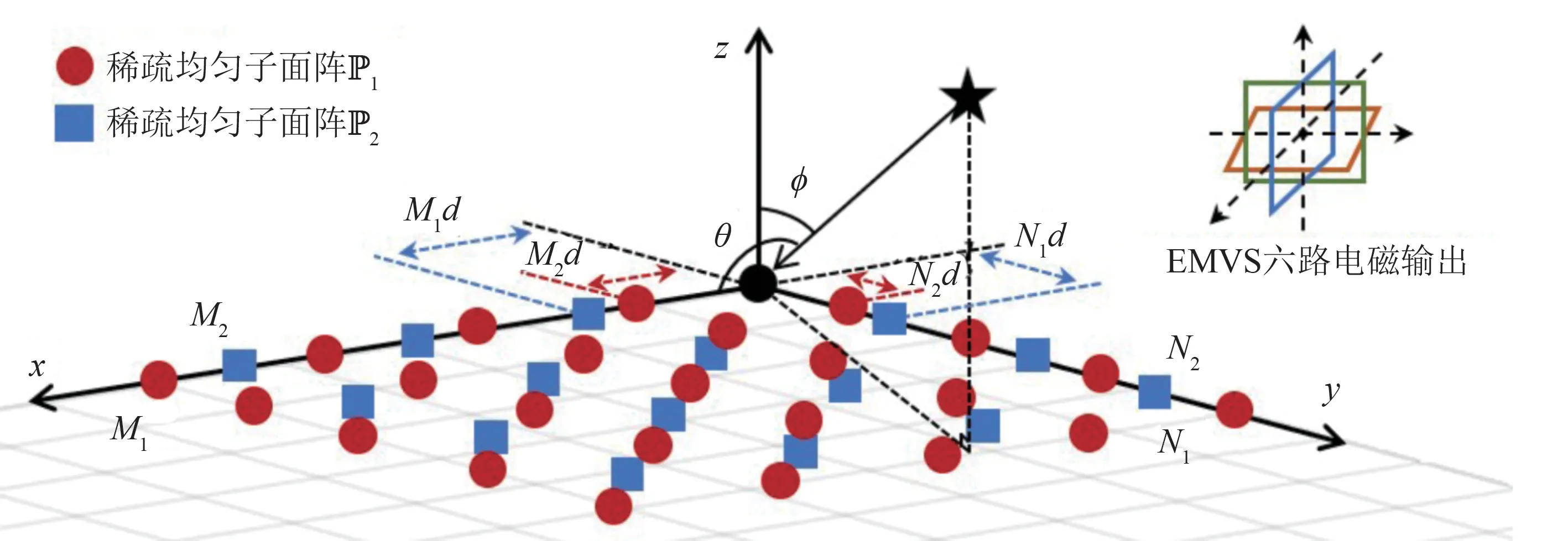
图1 EMVS互质面阵结构示意图(以M1=N1=5,M2=N2=4为例)Fig.1 EMVS coprime planar array geometry(M1=N1=5,M2=N2=4)
假设K个远场窄带非相关信号源从{(θk,ϕk),k=1,2,…,K}方向入射至EMVS 互质面阵,其中θk和ϕk分别表示第k个信号源的方位角和俯仰角,且θk∊[-π/2,π/2],ϕk∊[-π/2,π/2]。EMVS 互质面阵中各传感器阵元的六路输出同时包含了波达方向信息和极化状态信息,可表示为一个电磁响应矢量:
分别表示对应第k个信号源的空域响应矩阵和极化状态矢量,γk∊[0,2π]和ηk∊[-π,π]分别表示对应第k个信号源的极化辅助角和极化相位差,且
为了保留稀疏均匀子面阵Pi(i=1,2)在t时刻接收信号的多维电磁信息,即x轴方向、y轴方向的波达方向信息以及极化状态信息,将其建模为一个三维张量:
分别表示EMVS互质面阵在x轴和y轴方向上的导引矢量,对应第k个信号源,且μk=sinϕkcosθk,νk=sinϕksinθk,sk(t)为t时刻的采样信号,t=1,2,…,T,T为采样快拍数,◦表示外积操作,(∙)Τ表示转置操作,Ni(t)为t时刻独立同分布的加性高斯白噪声张量。进一步地,将所采集T个采样快拍的三维张量信号{Xi(t),t=1,2,…,T}在第四维度(即时间维度)上进行叠加,构造出稀疏均匀子面阵Pi的四维张量接收信号:
其中,sk=[sk(1),sk(2),…,sk(T)]Τ∊CT表示第k个信号源的多快拍采样信号矢量,Ni表示四维高斯白噪声张量。
3 面向EMVS 互质面阵的张量波束成形器设计
本节介绍所提面向EMVS互质面阵的张量波束成形器,包括稀疏均匀子面阵张量信号的空域滤波准则,张量化最小方差无畸变响应优化问题分解策略及对应的交替迭代求解方法,基于张量空间质数分解唯一性定理的稀疏均匀子面阵波束分布特性分析,以及基于波束功率互质合成的张量波束成形输出。
3.1 张量信号空域滤波准则设计
由于构成EMVS 互质面阵的两个稀疏均匀子面阵中的阵元排布不满足奈奎斯特采样定理,由此带来的相位模糊将导致波束功率图上产生虚峰,进而直接影响信源测向性能。为此,本小节从面向稀疏均匀子面阵张量信号的空域滤波准则入手,提出张量化最小方差无畸变响应优化问题,为后续剖析虚峰在波达方向平面上的分布特性并设计张量波束功率的互质合成方法提供理论基础。
具体地,针对稀疏均匀子面阵Pi在t时刻的张量接收信号Xi(t),设计一个具有相同三维结构的张量权重Wi∊CMi×Ni×6对其进行加权,如图2 所示,输出信号yi(t)可以表示为如下形式:
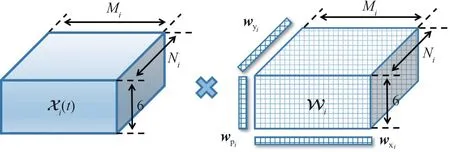
图2 稀疏均匀子面阵张量信号的张量权重加权示意图Fig.2 Illustration of spatial filtering of the sparse subarray tensor signals with a tensor weight

图3 张量波束功率互质合成处理框架示意图Fig.3 Illustration of coprime synthesis of tensor beam power
为了获得两个稀疏均匀子面阵所对应的张量权重Wi,需要最小化张量波束成形的平均输出功率,并保证波束扫描方向信号无失真,具体优化问题可表示为:
表示输出信号功率,
表示张量信号Xi(t)的六维协方差张量,
表示稀疏均匀子面阵Pi对应第k个信号源的三维导引张量,| · |表示复数的求模操作,E[·]表示取期望操作。这里,分别表示波束扫描的方位角和俯仰角,。在实际应用中,六维协方差张量Ri可通过计算Xi(t)的采样协方差张量近似得到,即:
式(9)所构造张量化最小方差无畸变响应优化问题以张量信号加权输出功率为优化目标,在极化辅助角γk和极化相位差ηk理想已知的条件下,当波束扫描至信号源波达方向上,即时,所对应张量波束功率呈现为最大响应,即在张量波束功率图对应位置上形成主瓣;由此,通过遍历波束扫描方位角和俯仰角的取值范围,能够在波达方向平面上有效反映信源的方位。
3.2 基于张量权重分解的交替迭代求解方法
由于优化问题(9)的优化目标和约束条件中包含张量外积和内积项,因此该问题是一个非凸优化问题。传统优化方法以矩阵信号处理和矩阵代数为基本前提,无法对所提张量化最小方差无畸变响应优化问题进行直接求解。同时,优化问题(9)的非凸属性也导致其无法提供一个闭式的全局最优解,严重影响了所提算法的实用性。为此,本文提出对张量权重进行分解,将原始优化问题(9)转换为对应波达方向信息维度和极化状态信息维度的子问题,并设计相应的交替迭代求解方法。具体而言,将三维张量权重Wi与Xi(t)的各空间维度信息逐一对应,可将Wi用canonical polyadic 分解的方式表示为对应于x轴波达方向信息、y轴波达方向信息和极化状态信息的波束成形权重矢量,具体形式如下:
将式(14)代入式(8)中,则采用张量权重Wi对张量信号Xi(t)的加权可等价表示为三个权重矢量对其进行结构化加权,如图2所示,则输出信号yi(t)可等价表示为:
其中,×r表示沿着第r维度的张量-矩阵内积操作。
基于式(15)的张量信号结构化加权形式,利用对应稀疏均匀子面阵Pi任意两个维度的权重矢量对Xi(t)进行加权,则相应的剩余维度,即x轴波达方向信息维度、y轴波达方向信息维度和极化状态信息维度的输出信号可分别表示为:
相应地,稀疏均匀子面阵Pi的张量波束成形输出信号yi(t)可等价表示为:
其中()·H表示共轭转置操作。将式(19)中输出信号yi(t)的三种等价表示形式代入张量化最小方差无畸变响应优化问题(9)中,可将其分解为以下三个子问题:
分别表示对应x轴波达方向信息维度、y轴波达方向信息维度和极化状态信息维度的协方差矩阵。由于这些子问题的优化目标和约束条件中均不包含张量,因此它们是凸优化问题,能够通过拉格朗日乘子法有效求得它们的局部最优解。
进而,根据这些子问题所对应空间维度信息的耦合关系,可以对它们进行交替迭代求解得到张量权重的全局最优解。具体而言,子问题(20)优化目标中的Rxi包含了其他两个子问题(21)、(22)中的优化变量wyi,wpi,子问题(21)优化目标中的Ryi包含了其他两个子问题(20)、(23)中的优化变量wxi,wpi,而子问题(22)优化目标中的Rpi包含了其他两个子问题(20)、(21)中的优化变量wxi,wyi,因此基于交替迭代优化的思想对上述三个子问题进行联合求解。首先,将波束成形权重矢量wxi,wyi和wpi初始化为,根据式(23)计算得到对应x轴波达方向信息维度的协方差矩阵Rxi;随后,利用拉格朗日乘子法求得子问题(20)的局部最优解:
将式(26)中的局部最优解wˉxi代入式(24)中计算协方差矩阵Ryi,并通过拉格朗日乘子法求得子问题(21)的局部最优解:
重复式(26)~(28)的优化过程交替迭代更新三个权重矢量,并在每次迭代中根据式(15)计算输出信号yi(t)的功率σ=|yi(t)|2。在第η次迭代中(η≥2),对比输出信号功率ση与前一次迭代所对应输出信号功率ση-1的差值,当Ξη=ση-ση-1≤δ时,上述三个子问题的交替迭代优化收敛,其中δ>0 表示一个预定义的收敛阈值。由此,通过序贯求解子问题(20)~(22),可以得到面向稀疏均匀子面阵Pi的全局最优张量权重以此为基础,下一小节通过研究两个稀疏均匀子面阵的波束分布特性,设计匹配阵元稀疏排布特点的EMVS 互质面阵张量波束功率处理方法,从而实现虚峰抵消的张量波束成形。
3.3 稀疏均匀子面阵的波束分布特性分析
定理1P1和P2所对应张量波束功率在信号源方向上形成主瓣,而在其他位置形成的虚峰互不重叠。
根据式(5)、(6)中导引矢量ai(μk),ai(νk)的定义,结合式(30)、(31)的等价关系,从ai(μk),ai(νk)的指数项推导可得[48]:
其中,P1,P2,Q1,Q2为非零整数。从式(32)、(33)中可得出以下关系:
然而,由于互质整数对(M1,M2)和(N1,N2)的最大公约数均为1,并不存在能够满足式(34)等价条件的非零整数P1,P2,Q1,Q2。因此,除了信号源方向(θk,ϕk)以外,并不存在其他模糊方向能够使得张量波束功率在对应位置上同时输出最大响应。由此可知,仅在对应信号源波达方向(θk,ϕk)的位置上形成主瓣,而在其他位置形成的虚峰互不重叠。证毕。
定理1 基于张量权重的可分解性,将张量化无畸变响应约束投影至不同维度上,利用张量空间的质数分解唯一性证明了EMVS 互质面阵中两个稀疏均匀子面阵所对应虚峰的互不重叠特性。该结论为后续通过稀疏均匀子面阵波束功率的互质合成实现虚峰抵消的张量波束成形提供了基础。
3.4 基于波束功率互质合成的张量波束成形
4 仿真实验
首先,通过绘制张量波束功率图开展仿真实验对比,以验证所提EMVS 互质面阵张量波束成形算法的有效性。考虑如图1 所示共包含40 个阵元的EMVS 互质面阵结构,假定两个信号源的入射方向分别为(θ1,ϕ1)=(15.5°,20.5°)和(θ2,ϕ2)=(45.5°,60.5°),对应已知的极化辅助角和极化相位差为(γk,ηk)=(40°,20°),k=1,2。所提算法的收敛阈值设置为δ=10-3,波束扫描的角度间隔设置为Δ=0.1°。在信源信噪比SNR=5 dB,采样快拍数T=300的条件下,在图4(a)、(b)中绘制稀疏均匀子面阵P1和P2的张量波束功率图,在 图4(c)中绘制基于乘积最小化处理的互质合成张量波束功率图,并将其分别投影至方位角维度和俯仰角维度上,如图4(d)、(e)所示。
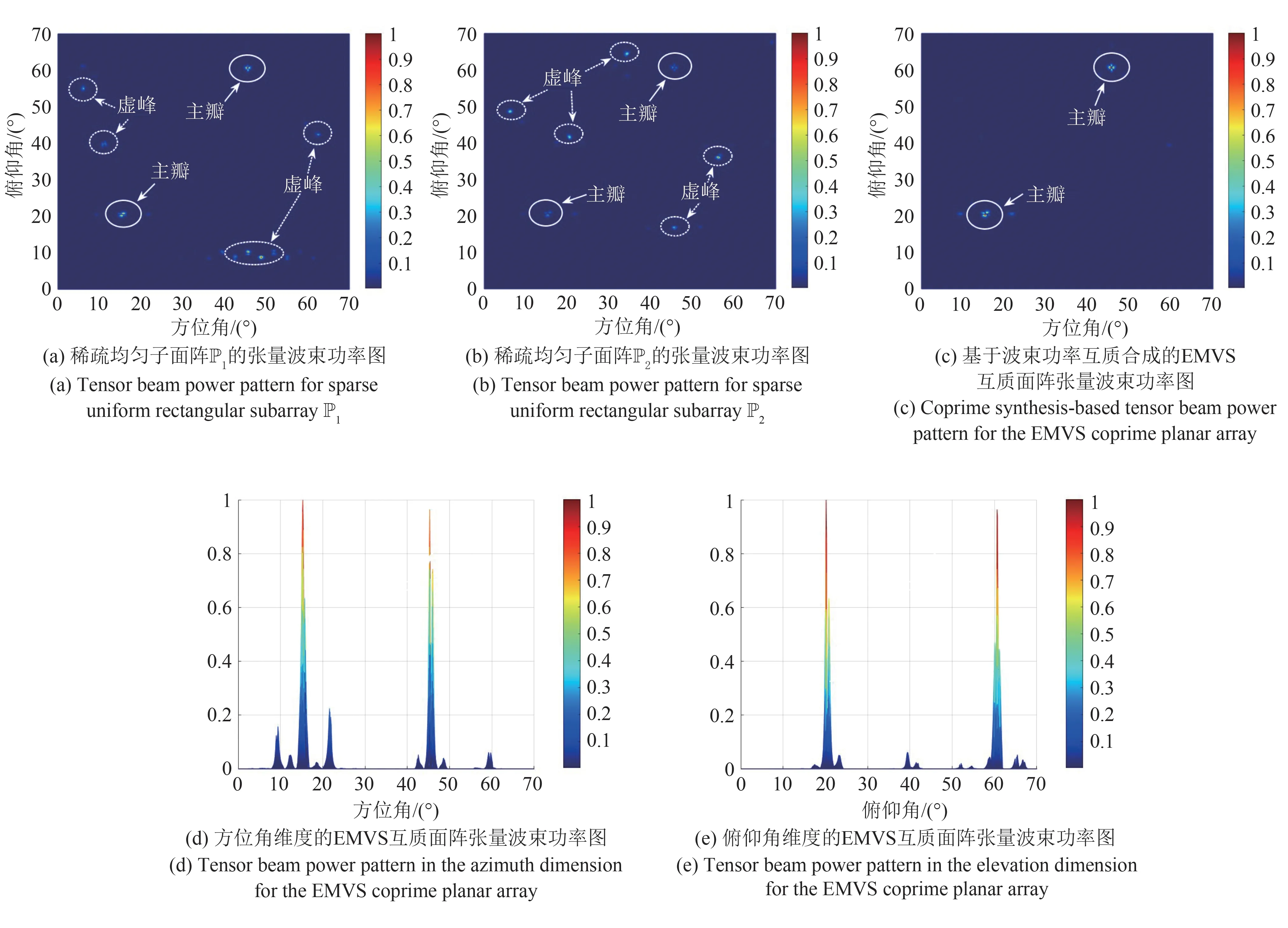
图4 所提EMVS互质面阵张量波束成形器的张量波束功率图Fig.4 Τensor beam power patterns for the proposed EMVS coprime planar array tensor beamformer
从图4(a)、(b)可以看出,得益于EMVS 六路输出中所涵盖的丰富空间电磁信息,以及所提张量信号的结构化空域滤波准则,两个稀疏均匀子面阵的张量波束功率均在对应信号源波达方向的位置上呈现为主瓣;然而,由于阵元的稀疏排布特性,在非信号源波达方向的位置上同时呈现出多个虚峰。根据3.3 小节所分析的稀疏均匀子面阵波束分布特性,所对应的虚峰位置互不重叠。通过对两个稀疏均匀子面阵张量波束功率进行互质合成处理,如图4(c)、(d)、(e)所示,EMVS 互质面阵的张量波束功率在对应信号源波达方向的位置上呈现出明显的主瓣,而在其他位置上的虚峰被有效抵消。
进一步地,对比所提EMVS 互质面阵张量波束成形器与EMVS 均匀面阵张量波束成形器[44]的波束成形输出性能。EMVS 均匀面阵按照5 行8 列的结构排布40个阵元,以保证阵元个数与EMVS互质面阵相同。假定两个信号源的入射方向分别为(θ1,ϕ1)=(20.5°,25.5°) 和(θ2,ϕ2)=(30.5°,45.5°)。在信噪比SNR=5 dB,采样快拍数T=300的条件下,绘制两种方法所对应的张量波束功率图,如图5(a)、(b)所示;在信噪比SNR=-10 dB,采样快拍数T=300 的条件下,绘制两种方法所对应的张量波束功率图,如图5(c)、(d)所示。
从图5中可以看出,在不同信噪比场景下,所提EMVS 互质面阵张量波束成形器的输出性能均优于采用相同阵元数目的EMVS 均匀面阵张量波束成形器。得益于EMVS 互质面阵的大孔径优势,所提EMVS 互质面阵张量波束成形器相较于EMVS均匀面阵能够输出更加精尖且能量集中的主瓣,在对应信号源波达方向的位置具备更强的波束指向性。与此同时,由于所提张量波束功率乘积最小化处理准则充分利用稀疏均匀子面阵的阵元互质排布特点削弱虚峰响应,EMVS 互质面阵张量波束成形器对应的张量波束功率图上无明显虚峰干扰,而EMVS 均匀面阵张量波束成形器所对应的张量波束功率图却仍存在较强的旁瓣,将对信源空间方位的精准刻画造成严重干扰。
最后,为了验证所提算法在信源测向精度上的优越性,将其与典型的EMVS 互质面阵虚拟域MUSIC方法[32],以及EMVS均匀面阵张量波束成形方法进行性能对比。假定两个信号源的入射方向分别 为(θ1,ϕ1)=(30°,25°)和(θ2,ϕ2)=(45°,52°),在图6中展示对这两个信号源进行测向的50次重复实验结果。在不同的仿真环境下,所提算法都能够精确的估计两个信号源的来波方向,而相比之下,虚拟域MUSIC方法存在较大的信源测向偏差。同时,在采用张量波束成形准则的条件下,EMVS均匀面阵由于孔径受限,也无法提供准确的测向结果。综合上述仿真结果,本文所提EMVS 互质面阵张量波束成形器充分利用了多维稀疏阵列的大孔径优势和阵元结构化稀疏排布特点,能够获得较EMVS 均匀面阵更加精尖的波束输出,以及较传统EMVS 互质面阵测向方法更为精确、稳定的波达方向估计结果,为实际应用场景中的高性能信源测向提供了保障。
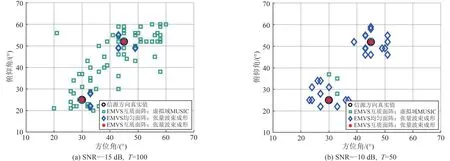
图6 信源测向结果对比图Fig.6 Comparison of source direction estimations
5 结论
本文综合考虑了EMVS 互质面阵的接收信号多维空间电磁信息结构和阵元稀疏排布特点,提出了一种EMVS 互质面阵张量波束成形算法。该算法构建了EMVS 互质面阵张量信号的结构化空域滤波准则,基于张量权重分解设计对应波达方向信息维度和极化状态信息维度的子问题,并提出针对子问题的交替迭代求解方法获得张量权重的全局最优解。在此基础上,分析了由两个稀疏均匀子面阵的阵元互质排布特点所带来的虚峰互不重叠特性,从抑制虚峰的角度设计了稀疏均匀子面阵张量波束功率的互质合成方法,从而在对应信号源波达方向的位置形成指向性波束。仿真结果表明,所提算法获得了优于现有EMVS 均匀面阵张量波束成形器的输出性能。
