多用户D2D计算卸载与资源分配算法
2024-03-07韩跃林
韩跃林 朱 琦*
(1.南京邮电大学江苏省无线通信重点实验室,江苏南京 210003;2.南京邮电大学教育部泛在网络健康服务系统工程研究中心,江苏南京 210003)
1 引言
智能终端的普及使得人们的生活发生了翻天覆地的变化,然而随着人工智能以及大数据的发展,应用程序运行时造成的开销也呈现爆炸性增长,这对于资源受限的移动终端带来了巨大的压力。移动边缘计算(Mobile Edge Computing,MEC)被视为解决终端设备压力的重要技术[1-2],通过将任务卸载到具有丰富计算资源的边缘服务器上进行处理,能够有效提高移动终端的任务处理效率,同时还能够减小终端的能量损耗[3]。
学术界对MEC 技术进行了广泛的研究。文献[4]针对单边缘服务器卸载时导致异地边缘服务器空闲状态下资源浪费问题,在云服务器与多个边缘服务器联合卸载的方案下,提出一种基于改进混合粒子群算法的边缘云协同计算卸载策略。文献[5]针对超密集组网(Ultra-dense Networks,UDN)的MEC 场景下的计算卸载场景,以任务卸载决策、信道分配决策和功率分配决策为优化变量,提出了以用户总能耗为优化目标的资源分配算法。文献[6]研究了任务存在依赖关系的场景下的计算卸载问题,提出了一种基于强化学习(Reinforcement Learning,RL)的无模型方法,旨在最小化受能耗约束的移动应用程序的执行时间。文献[7]考虑了异构网络中无线回程链路场景下的计算卸载问题,作者假设用户通过小基站与宏基站之间的无线回程链路传输将任务卸载到与宏基站相连的MEC 服务器上,通过优化用户任务卸载决策、服务器计算资源分配决策以及信道资源分配决策最小化所有用户的总开销。文献[8]研究了具有数据压缩的多用户MEC 系统的节能计算卸载。在任务卸载之前,对数据进行压缩以减小数据大小。在延迟约束条件下,考虑MEC 计算能力有限,通过联合优化计算卸载、数据压缩和资源分配来最小化能量消耗的问题。文献[9]提出了一种基于深度强化学习的节能算法来优化实时多用户MEC 系统的能耗。在多用户部分卸载场景下,形成了用户任务卸载比例与资源分配的非凸优化问题,为解决该问题,作者将能量最小化问题分解为任务卸载比例子问题和资源分配子问题,利用深度神经网络学习无线信道和卸载比之间的最优映射,并使用最优本地计算资源分配决策的闭式解和凸优化算法求解资源分配子问题。在车联网场景下,文献[10]考虑了由于车辆不同速度引起的通信环境的变化,通过联合优化多辆车的卸载比例和上行/计算/下行比特分配,使车辆在延迟约束下的总能量消耗最小化。在异构云(包括边缘云和远程云)场景下,为了进一步降低移动终端设备的能耗,提高计算资源的利用率,文献[11]提出了一种多计算资源协同任务卸载模型,并设计了该模型的适应度计算方法,提出了一种基于粒子群优化算法的多计算资源协同能量优化算法。
上述文献研究了MEC 中的计算卸载问题,然而MEC 的实施依赖于蜂窝网络的部署,在用户密集分布的场景下或者基站弱覆盖区域,边缘计算的增益效果将大大降低[12],因此业界提出了基于设备到设备(Device-to-Device,D2D)通信的计算卸载方案。文献[13]提出了一种面向联合学习的D2D 计算任务卸载方案,作者考虑不同边缘节点通过D2D通信交换数据样本,平衡节点的处理能力和任务负载,以最小化联合学习模型训练过程的总时延。文献[14]以最小化MEC 网络的任务延迟和终端能耗为目标,通过建立多目标约束的成本优化模型,提出了D2D 辅助MEC 网络中考虑任务卸载和计算资源分配的联合优化问题。文献[15]提出了一种基于网络辅助D2D 协作的新型移动任务卸载框架,移动用户通过网络运营商的控制辅助,可以动态、有益地共享计算和通信资源。作者旨在最小化所有用户的任务执行的单位时间能耗,同时提出了有效的激励机制防止用户过度占用公共资源和自私行为的发生。考虑到终端的移动性、用户的自私性和信息卸载不完整等因素,文献[16]在D2D 辅助的MEC 网络提出了一种整合迁移成本和卸载意愿的协同卸载框架。文献[17]研究了D2D 辅助MEC 的多用户联合协同部分卸载、传输调度分配和计算分配问题。考虑随机的应用程序请求、不可预测的MΤs 状态、时变的信道状态和计算资源,建立了一个定制的应用程序卸载模型,旨在同时最小化网络范围内的响应延迟和能量消耗。文献[18]假设部分用户有任务计算需求,并可以执行本地计算、MEC 卸载或D2D 卸载,任务可以划分为小数据,并可以通过各种计算模式同时执行,在此场景下研究了计算卸载和资源分配问题,提出了一种能够实现有效的信息交互和任务管理的联合任务管理体系结构。文献[19]将D2D 与MEC 结合以进一步提高蜂窝网络的计算容量,考虑用户任务可以同时进行D2D 卸载与MEC 卸载,通过优化D2D 设备匹配与MEC 计算资源分配以最大化蜂窝网络能支持的最大设备数。上述文献考虑了基于D2D 通信辅助的计算卸载场景,然而并没有着重研究D2D 场景下用户之间的利益竞争问题。在基于D2D 模式的计算卸载场景下,用户自身的自私属性以及移动设备有限的计算资源都会影响到用户之间的协作积极性,因此有必要对用户之间的利益竞争关系进行研究,通过合适的策略激励用户参与协作计算。
本文在多用户场景下对用户的计算卸载问题进行了研究。联合考虑具有计算需求的用户与能够提供计算服务的空闲用户双方的利益竞争关系,提出了一种基于D2D 通信的计算卸载与资源分配算法,该算法通过对需求用户的任务卸载决策和计算资源租赁单价决策以及空闲用户的计算资源分配决策进行优化,以最大化需求用户与空闲用户的效用。针对需求用户的计算资源租赁单价决策和空闲用户的计算资源分配决策,提出了基于斯坦柯尔伯格博弈(Stackelberg Game)的优化算法,针对需求用户的任务卸载决策,提出了基于遗传算法的优化算法,仿真结果表明,本文算法能够有效提高需求用户与空闲用户的效用。
本文剩余内容安排如下:第二部分给出了多用户单任务场景下的计算卸载系统模型;第三部分将给定需求用户计算卸载决策下各方用户的利益竞争问题搭建为Stackelberg 博弈模型;第四部分给出了Stackelberg 博弈均衡求解算法以及需求用户的任务卸载决策优化算法;第五部分进行了算法的仿真与分析;第六部分进行了总结。
2 系统模型
2.1 卸载模型
基于D2D 通信的计算卸载模型如图1 所示。在当前任务周期内,将基站覆盖范围内的移动用户分为两类,一类是具有任务计算需求的需求用户,另一类是无任务需要处理且能够对外提供计算资源的空闲用户。假设需求用户的总人数为N,用集合Ν={1,2,…,n,…,N}表示,空闲用户的总人数为I,用集合Ι={1,2,…,i,…,I}表示。假设每个需求用户有一个计算密集型任务,用户n的任务可用{Cn,Dn,Ln}表示,其中Cn表示计算任务所需要的CPU 执行周期,Dn表示任务的数据量大小,Ln表示任务的最大容忍延迟。Cn与Dn之间满足关系Cn=κnDn,其中κn计算每比特数据量的任务所需要的CPU 周期数,反映了任务计算的复杂度。对于任意需求用户的任务,用户可以选择将任务在本地终端设备上处理,也可以将任务以整体卸载的方式卸载到空闲用户终端上进行处理,并支付一定的费用给空闲用户,用户之间进行D2D 时不存在信道干扰。xn,loc表示需求用户n任务本地执行的标志,如果xn,loc=1,则表示用户n选择将任务置于本地执行,如果xn,loc=0,则表示用户n选择将任务进行卸载。xn,i表示需求用户n与空闲用户i的D2D 卸载标志,如果xn,i=1,则表示用户n选择将任务卸载到空闲用户i的终端上处理,如果xn,i=0,则表示用户n选择将任务卸载到空闲用户处理。假设每个空闲用户最多只能处理一个任务,即对于任意空闲用户i∊Ι,均满足

图1 基于D2D通信的计算卸载模型Fig.1 D2D communication-based computation offloading system
2.2 开销模型
为了提高用户体验,本文联合考虑了任务完成时延,终端能耗以及可能涉及到的任务卸载费用等多方面的用户开销。同时也考虑了空闲用户在协作计算卸载过程中的收益,并建立了Stackelberg 模型,以最大化多方的利益。对于需求用户n而言,其任务具有两种处理模式,分别是本地执行和卸载到空闲用户终端上执行。下面针对这两种模式对需求用户n的开销进行分析。
(1)本地执行
对于需求用户n,若其任务在本地执行,则设备消耗的能耗En,loc可以表示为[20]
其中,αn为用户n终端设备能耗系数,该值与设备CPU的结构有关。fn为用户n终端本地的计算能力。
用户任务的处理完成时延Tn,loc可以表示为
(2)D2D卸载
如果需求用户n选择将任务卸载到空闲用户i终端上处理,则用户n终端的能耗为发送任务所需要的通信能耗。需要说明的是,由于任务处理结果一般数据量较小,因此本文不考虑设备接收任务处理结果需要消耗的能量。在此情况下,设备消耗的能耗En,i可以表示为
其中,Pn表示用户n终端设备的发射功率。Rn,i表示用户n与用户i的信息传输速率,Rn,i具体表示为
其中,Wn,i表示用户n终端与用户i终端之间的可用信道带宽,hn,i表示用户n终端与用户i终端之间的信道增益,σ2表示加性高斯白噪声功率。
在D2D 卸载模式下,用户任务的处理完成时延Tn由两部分组成,分别是任务传输至用户i终端的时延与用户i终端计算任务的时延,因此,Tn,i可以表示为
其中,fi,n表示用户i向用户n提供的计算能力。
为激励空闲用户参与协作计算,用户n在向用户i卸载任务的同时需要支付一定的费用作为任务计算酬金。假设用户n以单价租赁的方式占用空闲用户i终端的计算资源,用pn,i表示用户n向用户i给出的计算资源租赁单价,则用户n需要向用户i支付的费用可以表示为
在协作计算中,空闲用户终端的开销为计算任务消耗的能量,其中任意空闲用户i的能耗可以表示为
其中,αi为空闲用户i终端设备的能耗因子,该参数与设备CPU的结构有关。
2.3 效用函数
本文定义需求用户的效用为相较于本地计算模式下的用户总开销的减小值,联合考虑任务完成时延,用户终端设备能耗以及计算资源租赁费用等三方面的用户开销,则需求用户n的效用函数定义为:
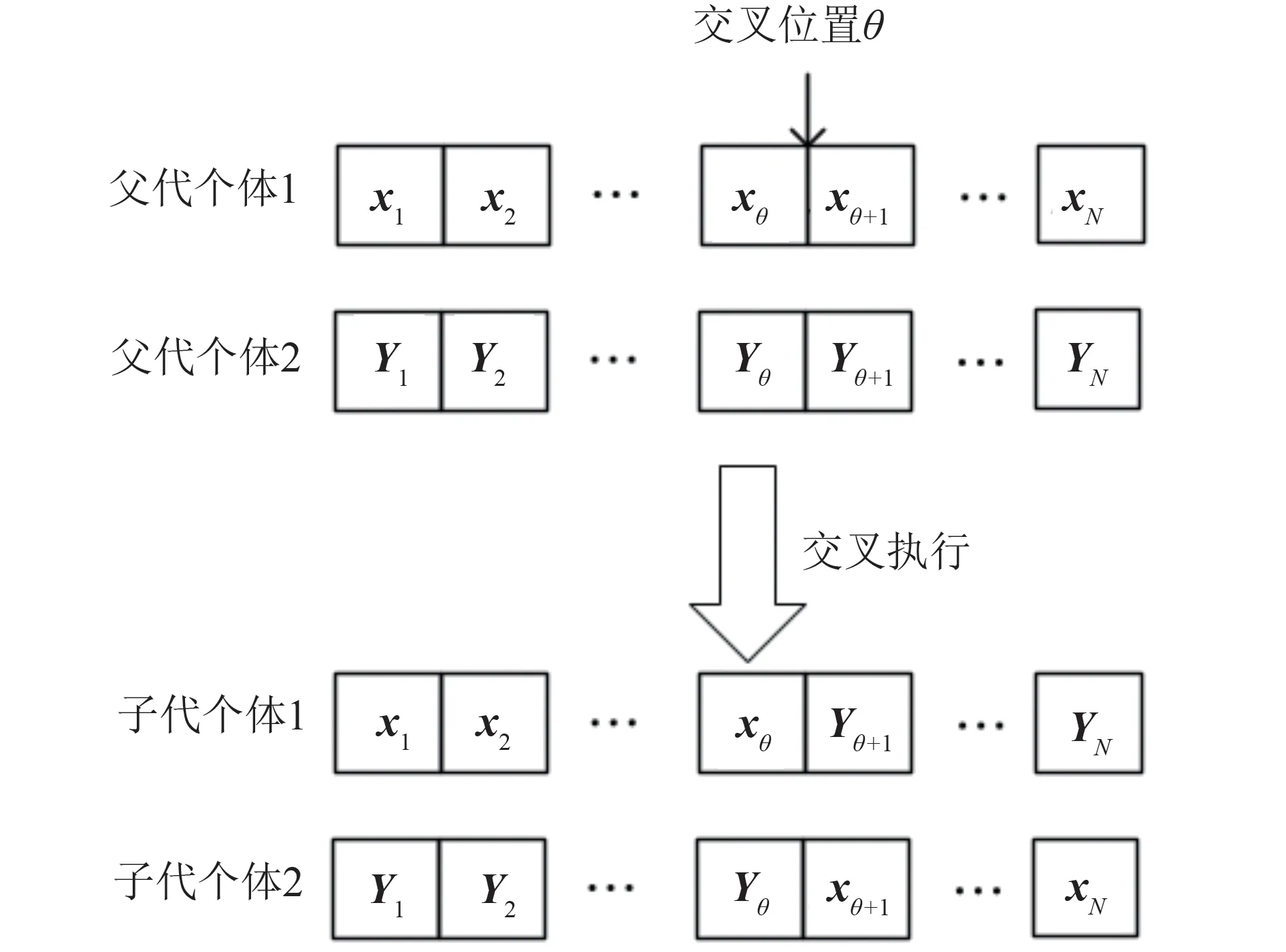
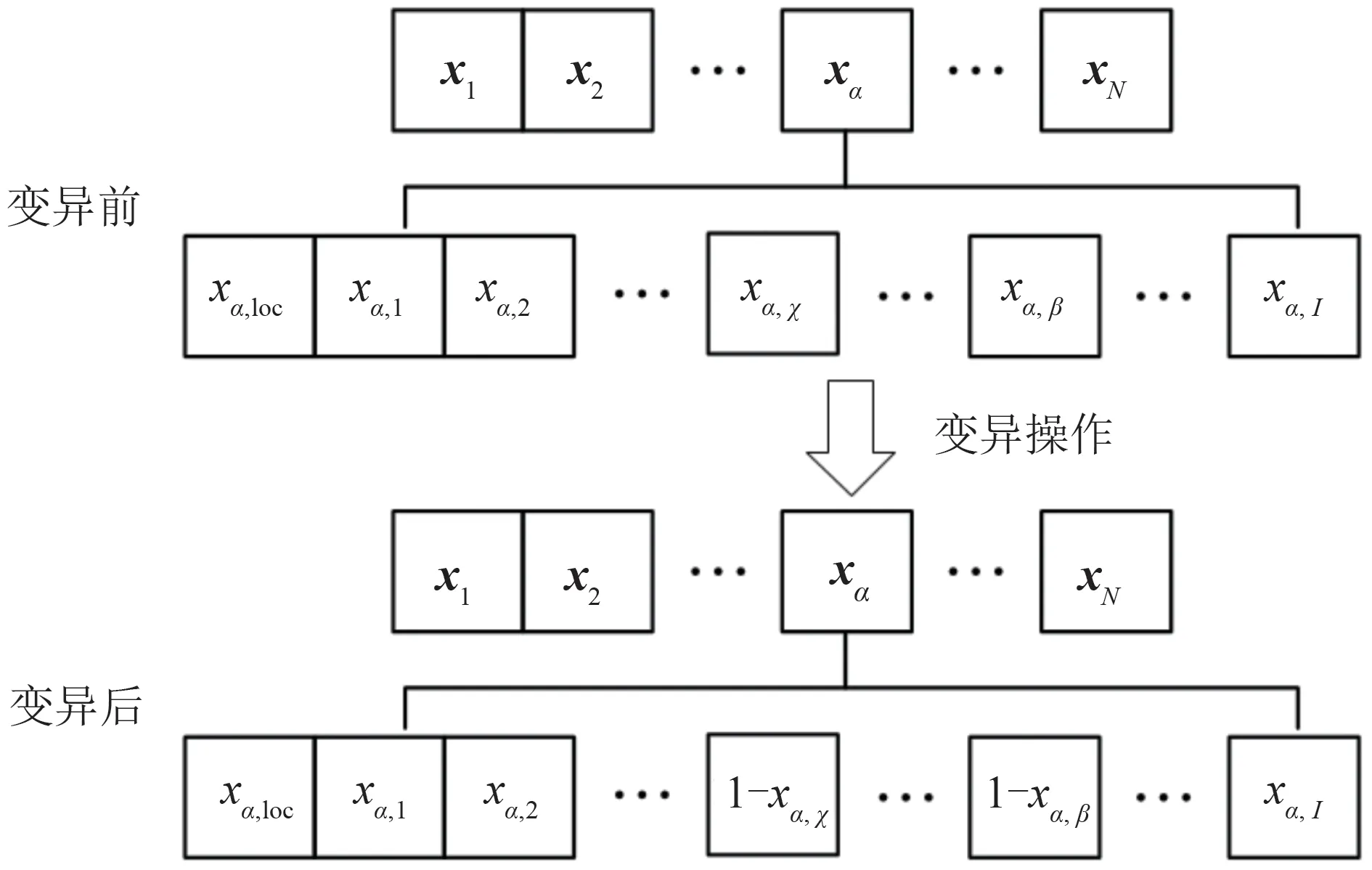
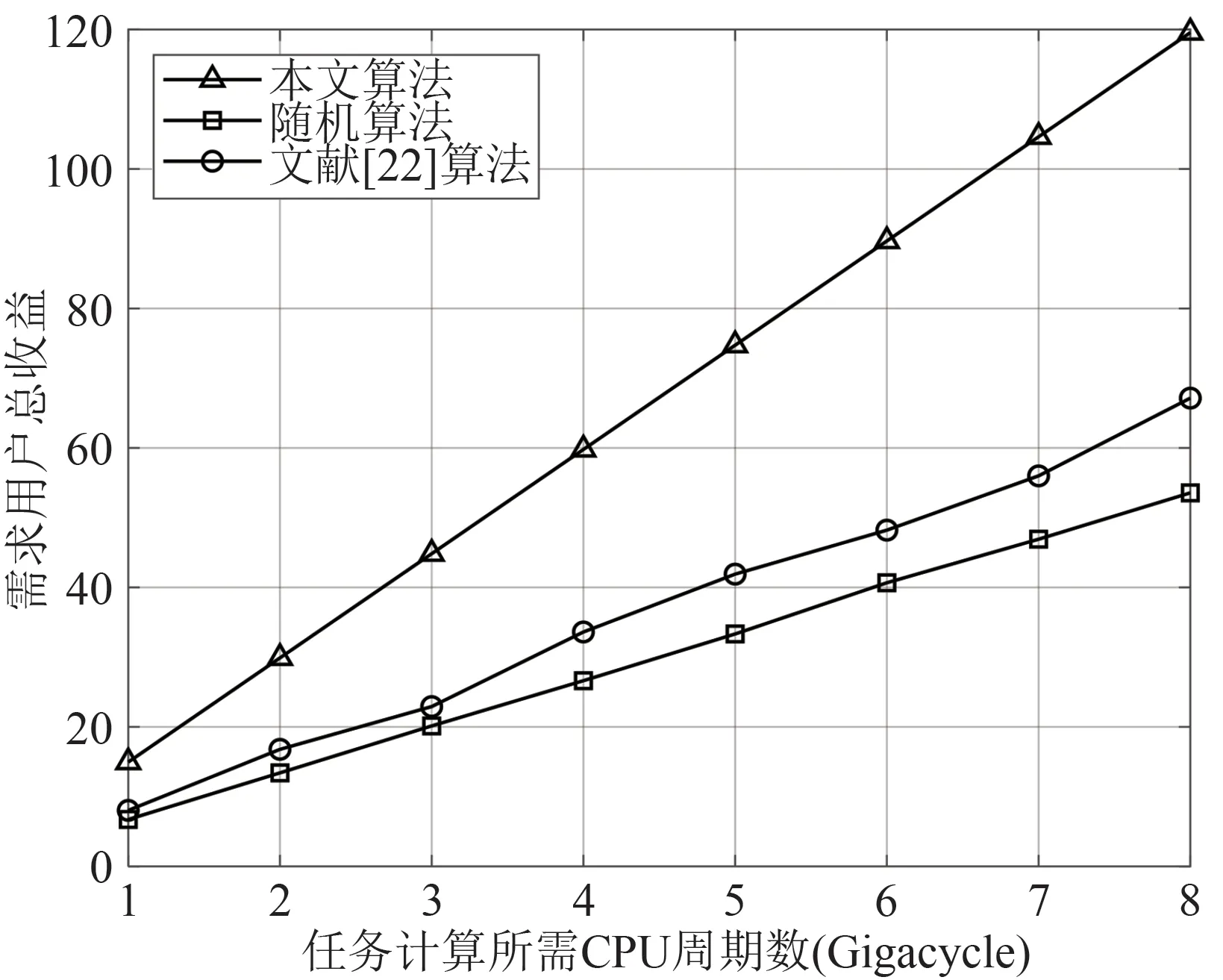
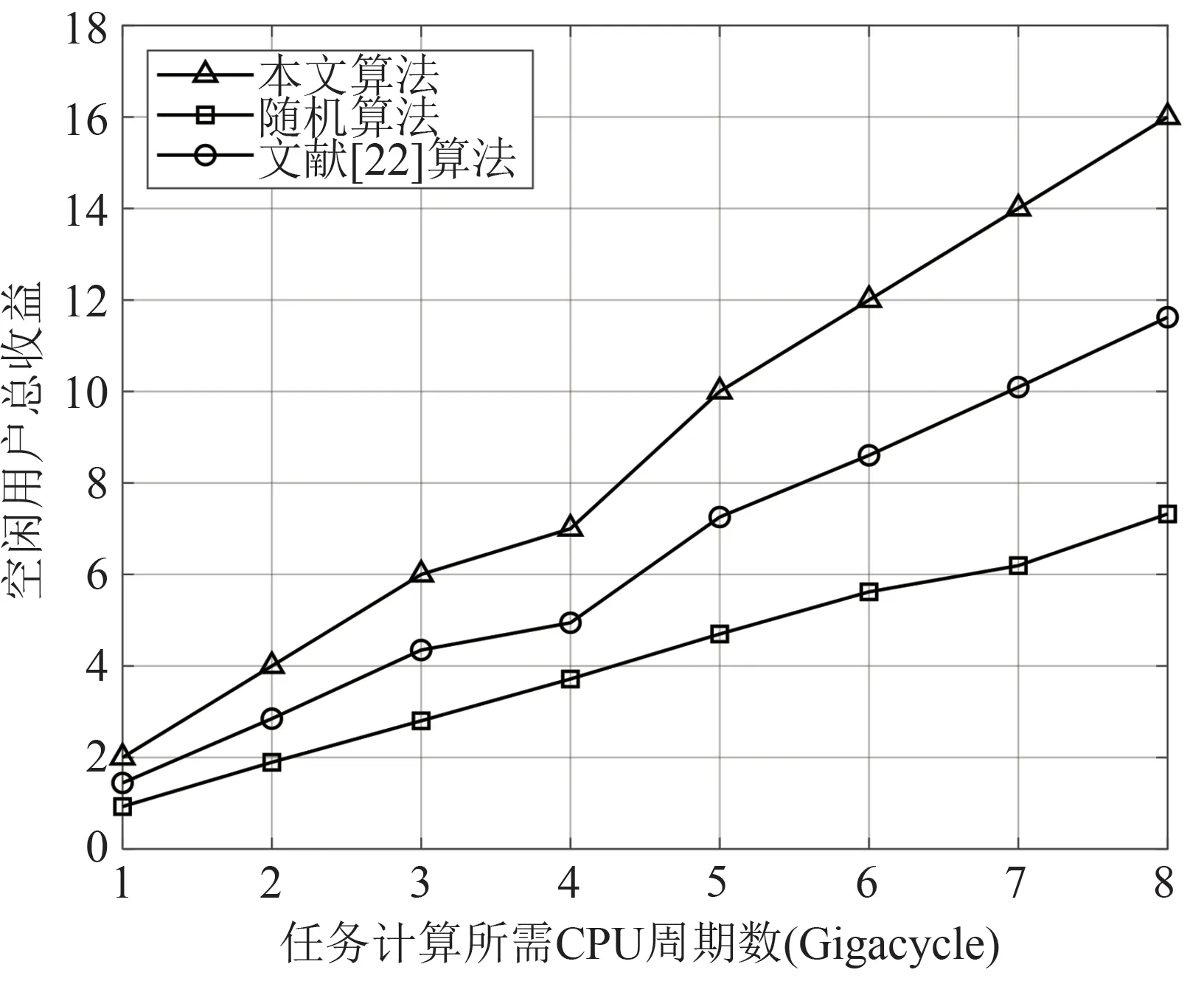
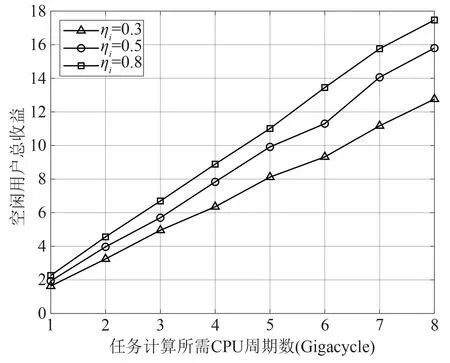
其中,λn表示任务在最大容忍延迟内完成带来的收益因子,如果任务Tn 定义空闲用户的效用为除去开销后协作需求用户计算任务所获得的收益,对于任务空闲用户i,其效用函数可表示为 其中,ηi为能耗加权因子,反映了空闲用户对能耗的重视程度。 本节联合考虑协作计算中需求用户与空闲用户多方的利益,首先根据各方的效用函数构建了相应的优化问题,接下来结合卸载方(需求用户)与服务方(空闲用户)之间的相互作用关系,建立了Stackelberg 博弈模型。在Stackelberg 博弈模型中,需求用户作为领导层,空闲用户为从属层。领导层根据任务卸载决策对计算资源租赁单价具有优先报价权,从属层根据需求用户提供的计算资源租赁单价决定提供的计算资源大小,使得自身目标效用最大化,双方基于计算资源租赁单价与可提供计算资源进行博弈。 对于任意需求用户n,其在计算卸载过程中的决策包括任务卸载决策{xn,loc,xn,i}和计算资源租赁单价pn,i,其中i∊Ι。用户n的优化问题可以表示为 其中,约束C1 表示用户任务只能在一处执行,约束C2 规定了计算资源租赁单价的上下限,表示用户n计算资源租赁单价的下界,表示用户n计算资源租赁单价的上界。 对于任意空闲用户i,其在协作计算过程中的决策为向需求用户提供的计算资源,用户i的优化问题可以表述为 其中,约束C3 表示用户i为需求用户提供的计算资源不能超过设备限制。 假设每个需求用户以整体卸载的方式进行任务卸载,为了提高空闲用户参与协作计算的积极性,考虑需求用户与空闲用户之间以博弈论的方法进行计算资源议价,作为领导层,需求用户在任务卸载决策决定方面具有绝对主导权。考虑在给定需求用户的任务卸载决策{xn,loc,xn,i}基础上,对需求用户与空闲用户的剩余变量进行优化,使得双方在此基础之上的效用最大化。本文对于Stackelberg博弈均衡的定义如下: 定义1(Stackelberg 博弈均衡)假设x={xn,loc,xn,i}n∊Ν表示当前所有需求用户的任务卸载决策,为需求用户n的最优计算资源租赁单价决策,表示空闲用户i的最优计算资源决策。在所有的解情况中,Stackelberg 博弈均衡可以表示为),该均衡点满足以下条件: 定理1给定所有需求用户的卸载决策x={xn,loc,xn,i}n∊Ν,需求用户与空闲用户的决策存在唯一纳什均衡。 证明: 对于空闲用户i,假设需求用户n的任务卸载决策xn,i=1,则用户i受需求用户计算资源租赁单价影响下的效用函数可以表示为 对上式求导分别得到其一阶导函数与二阶导函数如下: 将需求用户的计算资源租赁单价变化区间边界值分别对应fi,n=0与fi,n=Fi的情况,得到 对任意需求用户n,其最优决策必定在与之间,所以空闲用户的最优决策可以表示为 对上式求导分别得到其一阶导函数与二阶导函数如下: 故在给定所有用户的任务卸载决策x={xn,loc,xn,i}n∊Ν下,Stackelberg 博弈存在唯一纳什均衡,证毕。 本节针对需求用户与空闲用户的优化问题提出了相应的求解算法。在给定需求用户任务卸载决策下,针对计算卸载中卸载方(需求用户)与服务方(空闲用户)之间的利益博弈问题提出了纳什均衡求解算法,以兼顾各方的效用。针对需求用户的任务卸载决策问题,提出了基于遗传算法的启发式优化算法,以提高需求用户的收益。 如算法1 所示,在算法起始阶段,首先需要输入当前所有需求用户的任务卸载决策x={xn,loc,xn,i}n∊Ν,因为任务卸载决策下将会影响到纳什均衡结果。在初始化阶段,令当前迭代周期τ=0,并规定算法迭代收敛的精度需求ε,假设当所有需求用户的效用总和满足时,算法迭代终止。将所有需求用户的起始计算资源租赁单价设为po,其中的具体值可以由公式(19)和(20)计算得出。在{pn,i}n∊Ν=po的基础上,可以根据公式(21)求出当前空闲用户的最优决策{fi,n}i∊Ι,并结合公式(9)计算出当前各需求用户的效用{Un(τ)}n∊Ν。如算法1步骤7~14 所示,在每次算法循环迭代过程中,首先对当前迭代周期进行操作τ=τ+1,如果需求用户选择在本地终端处理任务,则只需要根据公式(9)计算出用户效用。针对将任务卸载到空闲用户终端的用户,根据公式(25)对其计算资源租赁单价决策进行变更,紧接着根据公式(21)对相应空闲用户的决策进行变更,并根据公式(9)计算出当前需求用户本迭代周期内的效用。当算法迭代终止时,此时的{pn,i}n∊Ν与{fi,n}i∊Ι即为给定需求用户任务卸载下各用户的最优决策,记作)。需要说明的是,由公式(25)可知,给定需求用户任务卸载决策下,需求用的最优计算资源租赁单价决策是固定的,因此经过两轮报价后,需求用户与空闲用户的决策即可收敛至纳什均衡点,算法1 的时间复杂度为o(N)。 在算法1 的基础上,在给定所有需求用户的卸载决策下,可以求解出需求用户与空闲用户形成的Stackelberg 博弈问题的纳什均衡解,从而有效提高各方在计算卸载过程中的收益。当需求用户的任务卸载决策变化时,算法1求解出的结果也随之变化,这意味着需求用户的效用会受到自身任务卸载决策的影响,为了优化所有需求用户的任务卸载决策,本文给出了基于遗传算法的任务卸载决策优化算法,以进一步提高需求用户的收益,具体见算法2。 如算法2所示,在算法初始化阶段,首先对遗传算法的相关参数进行初始化,具体包括种群的个体数量,最大遗传进化次数,每次进化产生新个体数量和个体变异概率。考虑到每个需求用户的任务具有两种执行方式,即本地执行和D2D 卸载,故对任意用户n,其任务卸载决策可以用包含I+1的元素的一维向量xn={xn,loc,xn,1,xn,2,∙∙∙,xn,i,∙∙∙,xn,I}表示,则种群中个体的基因型可以用如图2 表示。值得说明的是,在将任务卸载决策映射为种群中个体时必须保证所有需求用户的任务决策满足条件(1)和C1,即需求用户的任务只能选择在一台设备上执行且每个空闲用户最多只能接收一个任务。 图2 任务卸载决策编码示意图Fig.2 Τask offloading decision encoding diagram 初始化阶段完成后,算法开始执行迭代。在种群的每一次进化周期(即算法迭代周期)内,首先对种群执行交叉操作,具体执行方式为从种群按照适应度优先的准则挑选两个个体作为父代,个体的适应度越大,则从种群中被选中的概率越大。种群在初始化时,假设所有个体的适应度相同。父代个体在执行交叉操作之前会首先确定交叉位置θ,θ为区间1 ≤θ≤N-1内的随机值,在交叉位置θ的基础上,父代个体执行交叉操作的具体方法如图3所示。 图3 交叉操作示意图Fig.3 Crossover-operation diagram 由于交叉位置具有随机性,因此产生的子代个体基因型对应的任务卸载决策可能不满足约束(1)和C1,所以有必要对新产生的子代个体进行校正,校正步骤如下: (1)针对所有空闲用户i,判断是否 大于1,如果是,找出卸载标志为1 的两个需求用户n1和n2,随机确定n∊{n1,n2},令xn,i=0。 (2)针对所有需求用户n,判断是否大于1,如果是,找出卸载标志为1 的两个空闲用户i1和i2,随机确定i∊{i1,i2},令xn,i=0。 (3)针对所有需求用户n,判断是否等于0,如果是,则找出当前没有接收任务的空闲用户,随机将需求用户与空闲用户进行匹配,在此过程中,需求用户也可选择将任务置于本地执行。 执行完上述步骤后,即可将子代个体纳入种群中,当产生新个体数量为时,种群开始进入变异阶段。 图4 变异操作示意图Fig.4 Mutation-operation diagram 在交叉操作与变异操作执行完成后,对将每个个体转换为需求任务的任务卸载决策x={xn,loc,xn,i}n∊Ν,根据算法1,可求出需求用户的最优计算资源租赁单价决策与空闲用户的最优计算资源提供决策,结合公 式(9)可进一步求出需求用户的效用总和,将此效用值记作当前个体的适应度,在选择阶段,根据个体适应度大小,挑选出适应度最高的个个体作为下一进化周期的种群。当算法达到最大迭代周期时,输出此时种群中适应度最高的个体基因型对应的任务卸载决策,即为需求用户的最终任务卸载决策x*。算法2的迭代次数由种群进化次数决定,在每个迭代周期内,交叉操作与变异操作的语句执行频次处于小于的常数量级,算法2 的执行频次为1,故算法2的时间复杂度为o(N)。 本文采用MAΤLAB对提出算法进行仿真,以验证其有效性。假设需求用户和空闲用户的位置随机生成,D2D 通信的最大通信距离为50 m,各通信链路之间的信道衰落根据大尺度衰落模型hA,B=计算,其中k为信道衰落系数,dA,B为通信节点A和B之间的空间距离,λ为信道衰落指数。其他相关参数如表1所示[21]。 表1 仿真参数Tab.1 Simulation parameters 为了进行性能分析,本文将所提出的算法与随机算法和文献[22]中的算法在相同参数设置下进行比较。其中,随机算法是指对任意需求用户n,其任务卸载决策{xn,i}i∊Ι和计算资源租赁单价{pn,i}i∊Ι在取值范围内随机生成,对于任意空闲用户i,其计算资源决策{fi,n}n∊Ν同样在取值范围内随机产生。文献[22]采用图论方法对任务卸载以及资源分配进行优化,且不考虑需求用户与空闲用户之间的利益竞争关系。 图5 和图6 给出了本文提出的算法与随机算法在不同任务计算量下的用户总效用对比图。其中图5 给出了需求用户总效用的对比图,图6 给出了空闲用户的效用对比图。假设需求用户与空闲用户的数量都为10,需求用户的本地计算能力为{fn}n∊Ν=2 GHz,随机算法下的用户效用为算法执行1000 次的平均结果。由图5 可以看出,在不同任务计算量{Cn}n∊Ν下,相比较于其他两种算法,本文算法都能有效提高需求用户的收益,这是因为本文采用Stackelberg博弈模型对需求用户与空闲用户之间的利益竞争关系进行了建模分析,通过求解纳什均衡得到了需求用户与空闲用户的最优决策,能够有效提高用户的效用。随机算法下的空闲用户与需求用户在进行决策时具有随机性,无法保证需求用户根据信道传输环境、空闲用户设备能耗因子以及空闲用户的能耗加权因子做出合理的任务卸载决策和计算资源租赁单价决策,因此在性能上不如本文算法。文献[22]算法没有考虑需求用户与空闲用户之间决策的相互作用关系,仅能够保证需求用户根据当前环境做出合理的任务卸载决策,但是不能够通过调整计算资源租赁单价决策以进一步提高自身效用。同时可以看出,随着任务计算量的增加,用户的效用也随之增加,这是因为当任务计算量增加时,需求用户可以通过将任务卸载向空闲用户,以节省更多的能量,因此用户效用呈上升趋势。 图5 需求用户总收益随任务计算所需CPU周期数对比图Fig.5 Comparison of total utility of demand users versus the number of CPU cycles required for task calculation 图6 空闲用户总收益随任务计算所需CPU周期数对比图Fig.6 Comparison of total utility of idle users versus the number of CPU cycles required for task calculation 由图6可以看出,与其他算法相比,在不同需求用户任务计算量{Cn}n∊Ν下,本文算法能够有效提高空闲用户的收益。这是因为,本文算法将凸优化理论应用于空闲用户的决策过程,能够在给定需求用户的计算资源租赁单价下求出空闲用户的最优决策,从而为空闲用户带来更高的效用,而随机算法和文献[22]算法无法保证空闲用户根据需求用户的决策做出最优计算资源分配决策,由图中可以看出,随着需求用户任务计算量的增加,空闲用户的效用也随之增加,这是因为当需求用户任务计算量增加时,需求用户愿意给出更高的计算资源租赁单价以减少自身能耗开销,空闲用户也因此能够获得更高的收益。 图7 和图8 给出了不同空闲用户与需求用户数量比例下的用户总效用对比图。其中图7给出了需求用户总效用的对比图,图8 给出了空闲用户的效用对比图。由图7 可以看出,随着空闲用户在人群中的占比增大时,需求用户的总收益呈现递增趋势,这是因为,当空闲用户的数量增加时,更多的需求用户可以通过D2D 的方式进行任务卸载,从而降低了需求用户终端的能耗开销,在一定程度上提高了需求用户的效用。同时可以看出,与随机算法相比,在不同空闲用户占比下,本文算法能够有效提高需求用户的总收益,这是因为,无论空闲用户数量占比高低,本文算法都能够根据当前环境为需求用户求解出合理的任务卸载决策。 图7 不同空闲用户与需求用户数量比例下的需求用户效用对比图Fig.7 Comparison of total utilities of demand users under different ratios of idle users to demand users 图8 不同空闲用户与需求用户数量比例下的空闲用户效用对比图Fig.8 Comparison of total utilities of idle users under different ratios of idle users to demand users 由图8 可以看出,随着空闲用户在人群中的占比增大时,空闲用户的总收益也随之增加,这是因为,当空闲用户的数量增加时,更多的需求用户将任务交由空闲用户处理,空闲用户在协作计算过程中的总收益增加。由图中可以看出,随着需求用户任务计算所需要的CPU 周期数增加,空闲用户的效用也随之增加,这是因为,任务计算所需要的CPU周期数的增加会使得需求用户在决策出的计算资源租赁单价更高,结合公式(21)和(25)可知,空闲用户将获得更高的收益。 图9 和图10 给出了不同空闲用户能耗重视因子ηi下的用户总效用对比图。其中图9给出了需求用户总效用的对比图,图10给出了空闲用户的效用对比图。由图9 可以看出,随着空闲用户能耗重视因子ηi的增大,需求用户的总效用呈现下降趋势,这是因为,当空闲用户的能耗重视因子ηi增大时,给定需求用户的计算资源租赁单价下,空闲用户愿意提供的计算资源减少,从而导致需求用户的任务处理时延开销增加,需求用户的效用也因此降低。 图9 不同空闲用户能耗加权因子下的需求用户效用对比图Fig.9 Comparison of total utilities of demand users under different energy-consumption-weighting factors for idle users 图10 不同空闲用户能耗加权因子下的空闲用户效用对比图Fig.10 Comparison of total utilities of idle users under different energy-consumption-weighting factors for idle users 由图10可以看出,随着空闲用户能耗重视因子ηi的增大,空闲用户的总效用呈现上升趋势。由公式(21)可知,空闲用户能耗重视因子ηi越大,当需求用户的计算资源租赁单价固定时,空闲用户提供的计算资源越少,从而减少了协作计算中的能耗开销,同时,由公式(25)可知,更高的能耗重视因子ηi会使得需求用户制定更高的计算资源租赁单价,因此空闲用户的效用会随着能耗重视因子ηi的增加而增加。 本文在多用户场景下,将用户划分为有任务计算需求的需求用户和能够提供计算资源的空闲用户,并分别分析了两种用户在计算卸载过程中的开销,构建了各方的效用函数。提出了分层结构的计算卸载与资源分配算法,其中内层采用Stackelberg博弈模型将需求用户与空闲用户之间的利益竞争关系进行建模,通过动态迭代算法求解出了该博弈模型的纳什均衡解,外层采用遗传算法对需求用户的任务卸载决策进行了优化。最后,本文通过MAΤLAB 仿真工具对本文算法进行了仿真。仿真结果表明,与随机算法相比,本文算法能够有效提高需求用户与空闲用户的效用。3 Stackelberg博弈模型
3.1 优化问题
3.2 Stackelberg博弈均衡
4 博弈算法与卸载决策
4.1 纳什均衡求解算法

4.2 任务卸载决策优化算法


5 仿真与分析




6 结论