挖掘条件内涵选择合适路径

■安徽省宁国中学 陈晓明

在平时考试中,不少同学对题目条件不知如何处理,从而造成解题受阻,失分现象严重。如何解决这样的问题呢? 下面通过实例说明解题要注重对题目条件内涵的挖掘,选择合适的路径解决问题,我们的解题水平得到提高,才能笑傲考场!

解析:如图1 所示,要求椭圆E的离心率,就是要构建关于椭圆中的基本量a,b,c的方程。于是想到在△MF1F2中利用正弦定理或余弦定理解决问题,只需求出|MF1|,|MF2|的长即可。 由已知条件可判断MN为∠F1MF2的角平分线,且∠F1MF2=120°,这与后面的条件”有什么关系呢? 条件“有什么用呢?

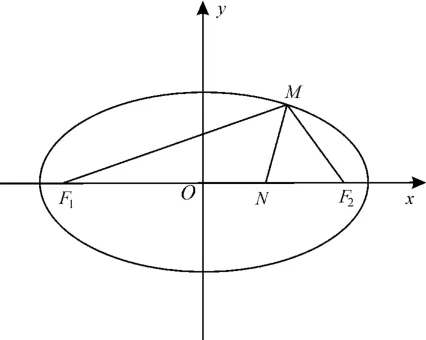
图1

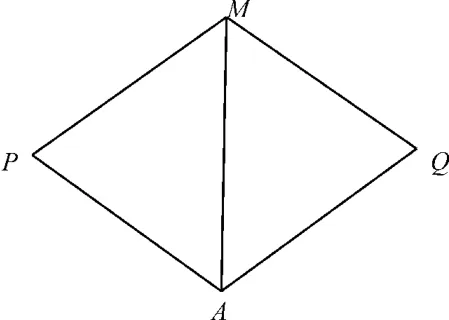
图2

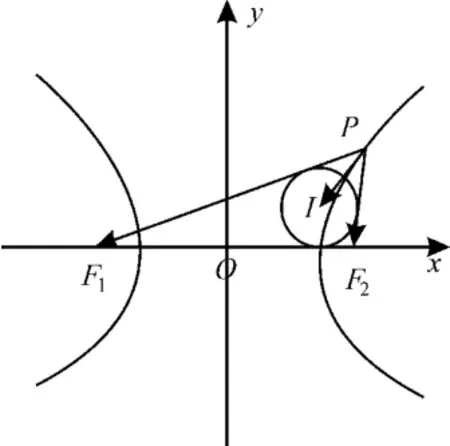
图3

于是还要从角平分线着手分析,三角形

再根据∠F1PF2=60°,由余弦定理得(2)2=9a2+a2-2×3a×a·cos 60°,解得a=2。

故△PF1F2的内切圆的半径为正确答案是B。

例2(安徽省2022 年高考考前适应性考试理科数学第20 题) 已知点O为坐标原点,过点C(4,0)的直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB。

(1)求抛物线的标准方程;

(2)动点M,N为抛物线在第一象限内两点,且直线MC与直线NC的倾斜角互补,求证:是定值。

解析:(1)如图4 所示,设A(x1,y1),B(x2,y2)。显然直线AB的斜率不为0,设其方程为x=my+4,代入抛物线方程y2=2px并整理得y2-2mpy-8p=0。

图4

因为根的判别式Δ>0,所以由韦达定理得y1y2=-8p。

(2)证法1 如图5所示,设点N关于x轴的对称点为T,则|ON|=|OT|。

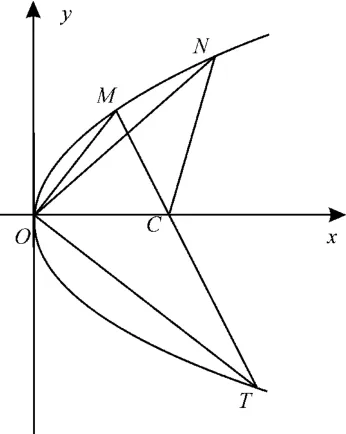
图5

因为直线MC与直线NC的倾斜角互补,所以M,C,T三点共线。

由 题 设 得OM⊥OT,不妨设M即为A点,T即为B点,即M(x1,y1),T(x2,y2),则N(x2,-y2),故y1(-y2)=x1x2+y1y2-2y1y2=-2y1y2=32,是定值。

点评:本证法充分挖掘条件“直线MC与直线NC的倾斜角互补”的内涵,得到M,C,T三点共线。从而由题设得OM⊥OT,再利用韦达定理、向量数量积的坐标表示及变换的思想解决问题。

证法2 如图6 所示,设M(x1,y1),N(x2,y2)。显然直线MN的斜率不为0,设其方程为x=my+a,代入抛物线方程y2=4x并整理得y2-4my-4a=0。

图6

当判别式Δ>0 时,由韦达定理得y1+y2=4m,y1y2=-4a。

因为直线MC与直线NC的倾斜角互补,所以它们斜率之和为0,即kMC+kNC=

又x1=my1+a,x2=my2+a,故y1(my2+a-4)+y2(my1+a-4)=0,整理得2my1y2+(a-4)(y1+y2)=0。

将y1+y2=4m,y1y2=-4a代入上式得-8ma+(a-4)·4m=0。

因为m≠0,所以解得a=-4。

点评:本证法充分挖掘条件“直线MC与直线NC的倾斜角互补”的内涵,得到kMC+kNC=0,从而利用斜率的坐标表示、直线方程消元、韦达定理及向量数量积的坐标表示解决问题。

因为y1+y2>0,所以y1y2=16。

点评:(1)本证法充分挖掘条件“直线MC与直线NC的倾斜角互补”的内涵,得到kMC+kNC=0,从而利用斜率的坐标表示、抛物线方程消元及向量数量积的坐标表示解决问题,没有利用韦达定理,解法变得简单。(2)仿照上述解题过程,我们易证下面结论成立。

已知定点C(2p,0),动点M,N为抛物线y2=2px(p>0)在第一象限内两点,若直线MC与直线NC的倾斜角互补,则是定值8p2。

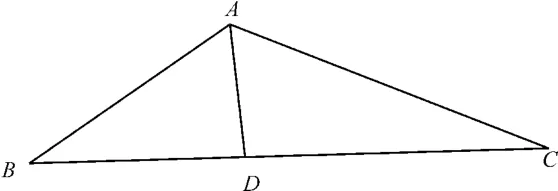
例3在△ABC中,角A,B,C的对边分别为a,b,c,已知(a+b)·(sinAsinB)=c(sinC+sinB),若角A的内角平分线AD的长为2,则4b+c的最小值为( )。

A.10 B.12 C.16 D.18

解析:因为(a+b)(sinA-sinB)=c(sinC+sinB),所以由正弦定理化角为边得(a+b)(a-b)=c(c+b),即b2+c2-a2=-bc。进一步由余弦定理得cosA=

又因为0

如 图7所示,已知A,又由题设知角平分线|AD|=2,仅这两个条件怎么能求出4b+c的最小值呢? 看来需要通过这两个条件来寻求边b和c的关系式,应该利用正弦定理或余弦定理来解决问题。

图7

再用余弦定理试试看: 在△ABC中利用余弦定理得。因为a未知,或者说根本没有利用条件“|AD|=2”,所以还是不行。

由两边及夹角可求三角形面积,于是想到了等面积法。

因 为S△ABC=S△ABD+S△ACD,所 以

将|AD|=2 代入并化简得bc=2(b+c),终于大功告成,构造了b和c的关系式。

这样问题就转化为一个我们比较常见的问题(“1”的代换)。

因为bc=2(b+c),所以故2(5+2×2)=18,当且仅当c=2b=6时等号成立,即4b+c的最小值是18,本题正确的答案是D。

点评:上述过程其实就是一步一步挖掘条件内涵,这时会出现条件的不同内涵,从而产生不同的解题路径,需要我们从中选择合适的路径解决问题。

同学们在平时的解题中,要注重对题目条件内涵的挖掘,这也有利于培养我们的发散思维,同时要结合结论,分析清楚不同的内涵产生的不同路径有的为什么不合适,怎样选择合适的路径是关键点。长期坚持,就不至于看到数学难题不知所措,从而我们的解题水平才能提高!