优化解题思路 提高解题素养——以导数中三类问题的优化为例

■河北南宫中学 韩文娟 霍忠林

不等式证明问题、函数恒成立问题、函数零点问题是导数中最常见的三种题型,这三种问题的“通性通法”就是:通过构造函数,将其转化为函数的最值问题来处理。对于函数的构造,是直接构造呢? 还是变形后再构造?不同的试题处理策略也是不同的。一般地,“先变形,再构造”往往能化繁为简,提高解题效率。下面通过几道试题让同学们感受“先变形,再构造”的魅力,提醒同学们解题时要有“变形”意识。

题型一、不等式证明问题

例1(2021年全国Ⅰ卷理科第20题改编)已知,证明:g(x)<1。

解析:由题意知函数g(x)的定义域为(-∞,0)∪(0,1)。

而f(0)=0,故f(x)>f(0)=0。

原命题得证。

评注:本题若直接构造函数f(x)=来处理,解题过程会涉及多次求导,计算也很烦琐,但是通过等价变形将对数ln(1-x)前的系数化为1,可以减少求导次数,优化解题过程,易于同学们掌握。实际上,在证明含有对数的不等式时,常通过等价变形将对数前的系数化为1,能优化解题过程。比如:在证明“形如f(x)·lnx>g(x)(或f(x)·lnx0)”时,可考虑将其等价转化为证明来处理,此时只要通过求导,一次便可将lnx“消灭”。

例2(2016年新课标Ⅱ卷理科第21题改编)证明:当x>0 时,(x-2)ex+x+2>0。

解析:当x>0 时,(x-2)ex+x+2>

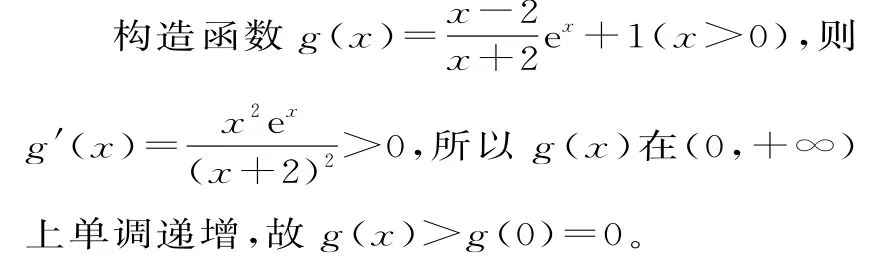
故原命题得证。

评注:若本题直接构造为f(x)=(x-2)ex+x+2 来证明,需要二次求导才能处理,但是通过变形,只需要求一次导即可。实际上,在证明含有指数的不等式时,常通过等价变形将指数与“其他部分”放在一起,往往能优化解题过程。比如,在证明“形如f(x)·ex>g(x)(或f(x)·ex0)”时,可考虑将其等价转化为证明”来处理,往往能提高解题效率。

题型二、函数恒成立问题

题型三、函数零点问题

通过上述几个例题,不难发现“变形”可以为解题带来便利,但是任何一种解题方法都不是万能的,并非所有的试题都一定需要变形。因此,同学们在日常的学习中要把知识和方法学“活”,不能盲目地照搬,遇到类似试题时要有“变形”的意识,这样才能避免思维僵化。