极值点偏移一击必中

■河南省濮阳市第一高级中学 袁 媛

极值点偏移问题是高考考查的重难点,通常作为压轴题出现,往往对思维要求较高,解题过程较为烦琐,难度较大,同学们处理起来比较困难,甚至无从下手。此类问题以导数为背景考查同学们运用函数与方程、数形结合、转化与化归思想解决函数问题的能力,层次性强。下面通过一题多解,系统地讲解处理极值点偏移问题的几种方法,使大家能够全面、准确地认识极值点偏移问题,掌握其解题技巧和方法,并且根据题目的特点,选择合适的方法,化难为易、化繁为简。

一、极值点偏移的定义

已知函数y=f(x)是连续可导函数,在区间(a,b)内只有一个极值点x0,f(x1)=f(x2),且x0在x1与x2之间,由于函数在极值点左右两侧的变化速度不同,导致函数图像不对称,使得极值点偏向变化速度快的一侧,常常有这种情况,称为极值点偏移。

二、极值点偏移问题的解题方法

例1f(x)=xlnx-2ax2+x,a∈R,若f(x)有两个极值点x1,x2,证明:x1+

证明:因为f(x)有两个极值点x1,x2,所以f′(x)=lnx-4ax+2有两个零点x1,x2。

令g(x)=lnx-4ax+2,则g′(x)=

分析可知a>0。

方法二(比值消参):

点评:对于与对数有关的极值点偏移问题,一般使用比值消参法,其目的是消参,所以先根据已知条件构造极值点具有的等式关系,然后作差。

方法三(对数均值不等式):

故lnx1-lnx2=4a(x1-x2)。

方法一(对称化构造):

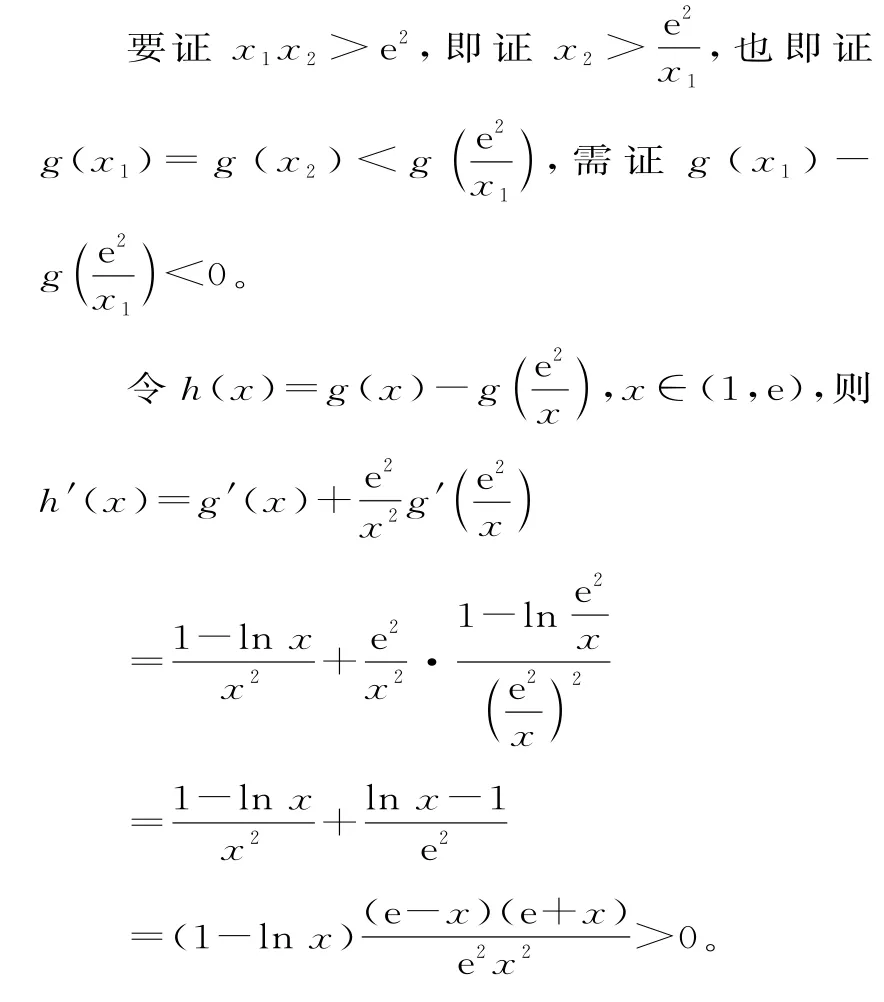
故h(t)在(1,e)上单调递增,h(t)

点评:若f(x1)=f(x2),证明x1x2>,对称化构造的答题模板如下:

(1)对f(x)求导,讨论函数f(x)的单调性,求出其极值点x0,然后确定x1,x2的取值范围,不妨令x1

(3)判断h′(x1)的正负,h(x1)的单调性;

(4)利用h(x1)的单调性,判断h(x1)的正负即可得证。

方法二(比值消参):

故h(t)在(0,1)上单调递增,h(t)

点评:利用比值消参时,也可以先将两个等式直接作商,得到含有的式子,再换元求解。

方法三(对数均值不等式):