高二期末考试模拟卷（B卷）参考答案与提示

一、单选题

1.C 2.A 3.D 4.B 5.B

6.C 提示:由题意得该几何体有6个面为边长为2的正方形,8 个面为边长为2的等边三角形。

在原正方体中建立如图1 所示的空间直角坐标系,原正方体边长为2,则A(2,1,0),F(2,2,1),D(1,2,2)。

图1

设E(t,1-t,2),0≤=(t-1,-1-t,0)。

7.D 8.C

二、多选题

9.ABD

10.ABD 提示:如图2所示。

图2

对选项A,由抛物线的焦半径公式可知|AB|=x1+x2+2≥2p=4,所以x1+x2≥2,故A 正确。

令直线l的方程为x=my+1,代入y2=4x得y2-4my-4=0,故y1y2=-4。

对于选项C,D,由|AA1|=|AF|可知∠AA1F=∠AFA1。

又AA1//OF,故∠AA1F=∠OFA1=∠AFA1,直线FA1平分∠AFO。

同理可得FB1平分∠BFO,故A1F⊥B1F,即∠A1FB1=90°。

因此,圆M经过点F,C错误,D 正确。

11.ABD 提示:A 选项,因为PA⊥平面ABCD,AB,AD⊂平面ABCD,所以PA⊥AB,PA⊥AD。

又四边形ABCD为正方形,故AB,AD,PA两两垂直。

如图3,以A为坐标原点,AB,AD,AP所在直线分别为x,y,z轴,建立空间直角坐标系。

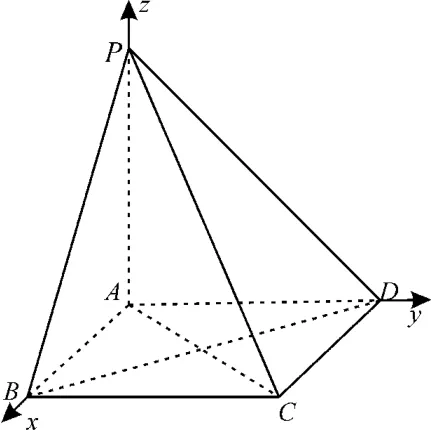
图3

则P(0,0,1),

B(1,0,0),A(0,0,0),C(1,1,0),D(0,

B选项,因为四边形ABCD为正方形,所以AC⊥BD。

又PA⊥平面ABCD,BD⊂平面ABCD,故PA⊥BD。

因 为AC∩PA=A,AC,PA⊂平 面PAC,所以BD⊥平面PAC。

直线PD与平面PAC所成的角为30°,B正确。

C 选项,设平面PBD的法向量为n=(x,y,z),则:

令y=1,得x=z=1,故n=(1,1,1)。

平面PAB的法向量为m=(0,1,0)。

平面PBD与平面PAB的夹角不为30°,C错误。

D 选项,由C 选项知,平面PBD的法向量为n=(1,1,1)。

故点C到平面PBD的距离,D 正确。

12.BCD 提示:对于选项A,如图4,过A、B分别作准线的垂线,垂足分别为E、D。当以AB为直径所作圆M与准线相切时,则

图4

由抛物线的定义可知|AE|=|AF|,|BD|=|BF|,所以|AF|+|BF|=|AB|。

显然此时AB经过焦点F。

但当直线l不经过焦点F时,圆M不一定与准线相切,故选项A 错误。

三、填空题

过点P作PN⊥x轴于点N,过A作AM⊥OP于点M,如图5所示。

图5

由椭圆的定义得,|PF1|+|PF2|=2a,则|PF1|2+|PF2|2+2|PF1||PF2|=4a2。

16.①②④ 提示:①连接BC1,DC1,由正方体的几何性质可得BC1//AD1,所以异面直线AD1,BD所成的角,即为BC1与BD所成的角∠DBC1。

因为△BDC1为等边三角形,所以∠DBC1=60°,故选项①正确。

因为BC1//AD1,且AD1⊄平面B1C1C,BC1⊂平面B1C1C,所以AD1//平面B1C1C。

则直线AD1上的任意一点到平面B1C1C的距离都相等,点F到平面B1C1C的距离为定值,选项②正确。

若F为AD1的中点,则点F到直线BD的距离为,选项③错误。

以点D为坐标原点,建立空间直角坐标系,如图6所示,则A1(2,0,2),C(0,2,0),A(2,0,0),D(0,0,0)。由三垂线定理 可 得,A1C⊥AD1,A1C⊥BD,故向量=(2,-2,2)是异面直线AD1与BD的法向量。

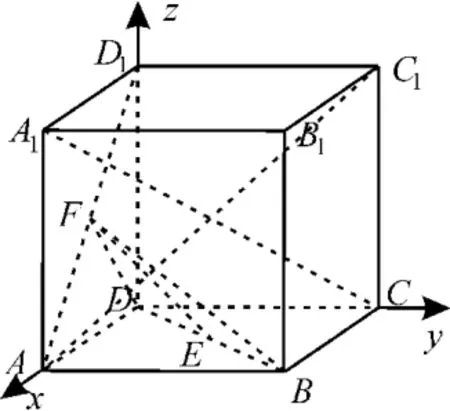
图6

四、解答题

所以直线AB的方程为y-1=2(x-2),即2x-y-3=0。

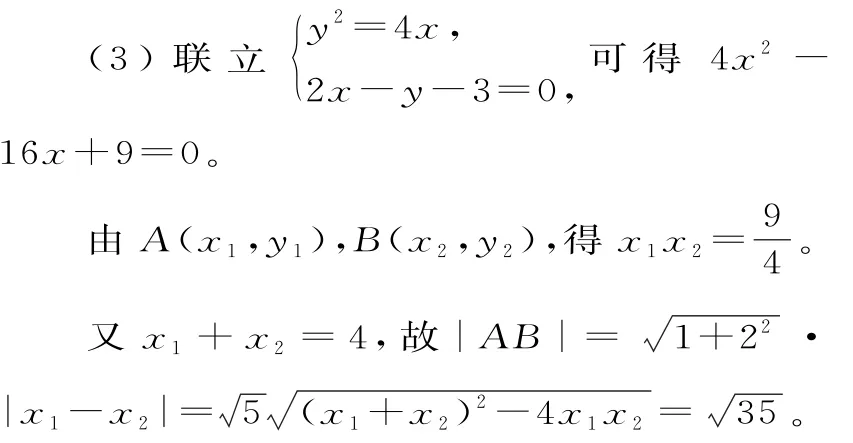
19.(1)圆C与y轴相切于点T(0,2),可设圆心的坐标为(m,2)(m>0),则圆C的半径为m。

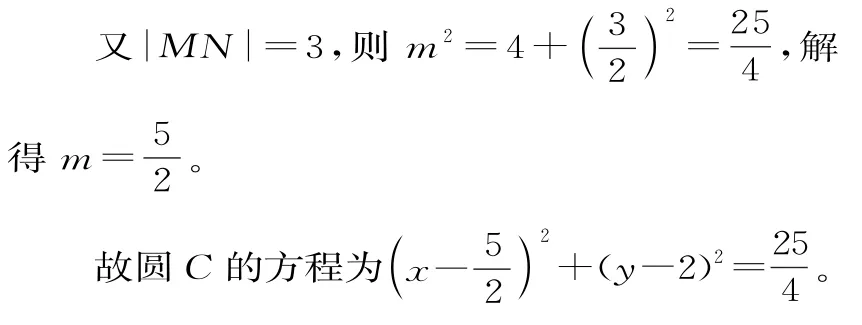
(2)由(1)知M(1,0),N(4,0)。

当直线AB的斜率不存在时,易知A,B关于x轴对称,kAN+kBN=0。

当直线AB的斜率为0 时,易知kAN=kBN=0,即kAN+kBN=0。

当直线AB的斜率存在且不为0 时,设直线AB:x=1+ty,将x=1+ty代入x2+y2-4=0,并整理得(t2+1)y2+2ty-3=0。

设A(x1,y1),B(x2,y2),则:

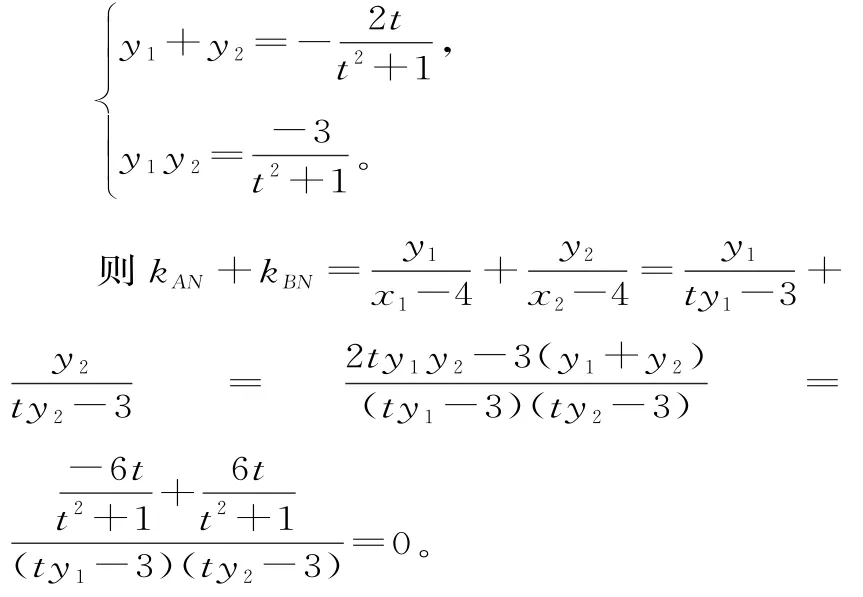
综上可知,kAN+kBN=0,为定值。

20.(1)若选①,如图7,取AC的中点G,连接EG。

图7

又|AG|=|AC|=1,|AE|=2,故|AG|2+|EG|2=|AE|2,AG⊥EG。

又CD//EG,则AC⊥CD。

又AC⊥BC,BC∩CD=C,BC,CD⊂平面BCD,故AC⊥平面BCD。

因为AC⊂平面ABC,所以平面ABC⊥平面BCD。

若选②,因为AC⊥BD,AC⊥BC,BC∩BD=B,BC,BD⊂平面BCD,所以AC⊥平面BCD。

又AC⊂平面ABC,故平面ABC⊥平面BCD。

若选③,如图8,取BC的中点O,AB的中点H,连接OD,OH,EH。

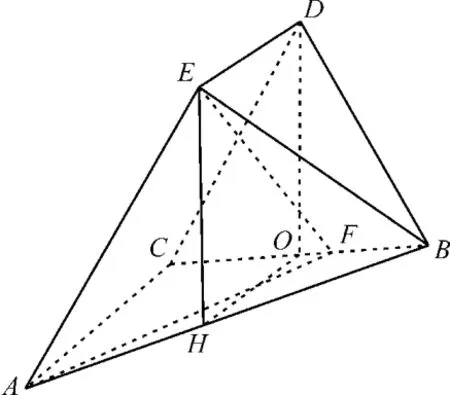
图8

因为|DC|=|BD|= 3,所以DO⊥BC。

又|BC|=2,故

又DE//AC,故AC⊥BD。

又AC⊥BC,BC∩BD=B,BC,BD⊂平面BCD,故AC⊥平面BCD。

因为AC⊂平面ABC,所以平面ABC⊥平面BCD。

(2)取BC的中点O,AB的中点H,连接DO,OH。

因为|BD|=|CD|,所以DO⊥BC。

又DO⊂平面BCD,平面BCD∩平面ABC=BC,故DO⊥平面ABC。

又OH//AC,AC⊥BC,故OH⊥BC。

综上所述,DO,OH,BC两两互相垂直。

则以O为坐标 原 点,,分别为x轴,y轴,z轴,建立如图9所示的空间直角坐标系。

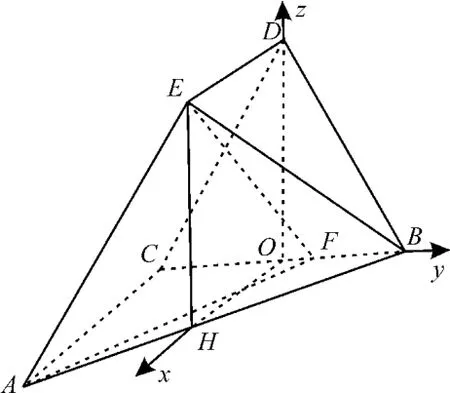
图9

图10

则A(2,-1,0),B(0,1,0),

21.(1)由题意可知,|PE|+|PF|=|PA|+|PE|=4>|EF|=2 3。

故点P的轨迹是以E,F为焦点,且长轴长2a=4的椭圆。

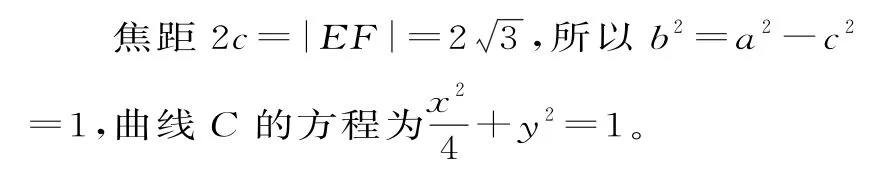
(2)(i)设P(x1,y1),Q(x2,y2),T(4,m)。

(ii)设直线PQ的方程为x=ty+n,P(x1,y1),Q(x2,y2)。

所以直线PQ的方程为x=ty+1,直线PQ经过定点(1,0)。

22.(1)依题意可知圆E的标准方程为(x+ 2)2+y2=16,圆心E(- 2,0)。

因为线段MF的垂直平分线交ME于点S,所以|SM|=|SF|。

动点S始终满足|SE|+|SF|=|SE|+|SM|=|EM|=4>|EF|=2 2,故动点S满足椭圆的定义。

曲线C是以E,F为焦点的椭圆,设椭圆方程为

因此,2a=4,2c=2 2。

解得a=2,b=c= 2,椭圆C的方程为

(2)存在与点P不同的定点Q(0,2),使得恒成立,理由如下。

当直线l与x轴平行时,由椭圆的对称性可知|PA|=|PB|。

当直线l与x轴垂直时,不妨设A(0,

若存在不同于点P的定点Q满足条件,则Q点坐标只能是(0,2)。

如图11,当直线l不平行于x轴且不垂直于x轴时,可设直线l的方程为y=kx+1。

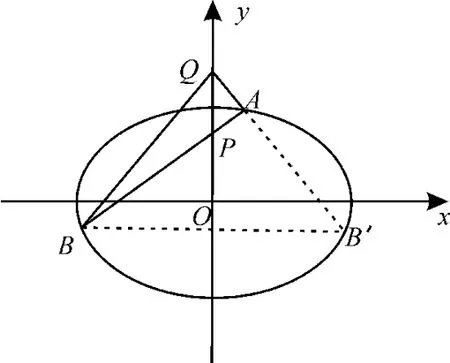
图11