移动场景下基于深度学习的图像辅助毫米波波束预测方案

李中捷，韦金迎，熊吉源，高伟

（中南民族大学 a.电子信息工程学院； b.智能无线通信湖北重点实验室， 武汉 430074）

高速无线通信的快速发展，促进了毫米波及大规模多输入多输出（Multiple Input Multiple Output，MIMO）天线系统的使用.虽然毫米波具有较高的传输带宽，但是其传播受限于严重的路径损耗.为了提高毫米波通信的可靠性，一般采用大规模MIMO 天线系统.通过配备数百个甚至数千个天线［1］，采用波束成形技术，可以显著提高网络传输的可达速率［2］.

由于传统的波束成形技术具有较大的控制开销［3-4］，因此对高速移动性用户的传输可靠性提出了重大挑战.针对控制开销问题，文献［4-7］尝试采用机器学习特别是深度学习方法作为数据驱动智能解决方案.如文献［5］提出一种基于深度学习方法，构建高维非线性关系，通过使用微波信道预测毫米波信道最佳波束索引，但是由于输入是高维的微波信道，该方案的时延和复杂度较高.文献［6］中通过混合噪声张量补全预测毫米波波束，需要对40%的离散位置进行功率测量，计算复杂度较高.文献［7］中提出利用创建知识数据库，使用过去用户检测内存来加快进入该区域新用户的波束向量.由于真实环境中数据量庞大，创建知识数据库会加剧计算复杂度提升，导致系统冗杂.以上方案均涉及到复杂度高的问题.

目前采用深度学习的大部分研究工作集中在无线感知数据上，通过无线接收数据驱动智能解决方案的学习和部署.文献［8-9］提出一种利用激光雷达和深度图像辅助无线通信的方案.文献［10］提出一种基于视觉辅助的波束及阻碍预测方案，并证明该方案可行.文献［11］提出一种深度学习协同波束成形方案，利用卷积神经网络从多个基站接收的导频信号中直接预测最佳波束，可以显著减少对准开销.文献［12］提出一种利用车辆位置信息和多路径指纹数据库的波束对准方案.文献［13］提出了一种基于RGB 和深度摄像机的主动式毫米波通信基站选择系统，用于预测用户阻塞情况.以上工作表明通过视频图像或用户坐标辅助预测最佳波束可行.

为了解决移动环境下，毫米波大规模MIMO通信系统的可靠性传输问题，本文提出一种基于深度学习的视频图像辅助波束预测方案，提升系统可达速率和降低模型复杂度.该方案利用文献［14］中的ViWi数据集，训练学习深度神经网络参数，用于建立通信环境中用户图像和最佳毫米波波束向量的非线性关系.通过基站RGB 相机采集的RGB 视频图像.在部署于基站的移动边缘计算（Mobile Edge Computing，MEC）服务器上将图像作为Faster RCNN 网络模型［15］的输入，进行目标检测，并在输出层后添加DNN 神经网络模块预测毫米波下行链路的波束向量.仿真结果表明：本文算法和基线算法相比，能够显著降低模型复杂度，且趋近于最优的可达速率.

1 系统模型

图1所示为高速移动环境下的毫米波无线通信系统模拟图.基站部署了MEC服务器，并配置毫米波大规模天线阵列和RGB相机，移动用户配置单天线.大规模天线阵列采用平面阵列（Uniform Linear Array，ULA），总天线数量为Nr.基站RGB 相机拍摄覆盖范围内的通信环境图像，上传到MEC 服务器进行处理.该系统采用正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）技术，基站与移动用户毫米波信道定义为：

图1 毫米波MIMO通信系统模拟图Fig. 1 Simulation diagram of millimeter wave MIMO communication system

式中：L是信道路径数，K是子载波个数，p是余弦脉冲整形函数，a是阵列响应向量，aℓ，τℓ，θℓ，φℓ分别是第ℓ信道路径的路径增益（包括路径损耗）、延迟、到达方位角和仰角，TS为采样时间，D为循环前缀长度（假设最大延迟小于DTS）.

假设毫米波基站大规模MIMO 天线系统采用模拟波束成形架构，每个波束成形向量f的波束成形权重由恒模移相器实现.毫米波下行链路波束成形向量从码本中选取，其中码本定义为：

第n个波束成形向量定义为：

式中：d是天线间距，ωn是转向角，a(ωn)是在ωn方向上的阵列转向向量，Nr是天线数量.

将F中的波束成形向量索引定义为：

波束向量是通过索引I选取波束码本中所对应的向量，得到最佳波束向量f*.将该波束向量用于下行数据传输，则用户接收的信号表示为：

式中：h∈CNr×K为毫米波信道，s为传输信号，n～NC(0，σ2)为高斯噪声样本.

2 图像辅助波束预测深度学习方案

本文提出的图像辅助毫米波波束预测深度学习方案，采用目标检测方法定位通信环境中移动用户的位置，根据检测出的用户坐标预测最佳波束向量，实现毫米波下行链路的可靠性传输.该方案中波束预测是基于码本的选择，找到为用户服务的最佳波束向量f*，从而使该用户下行链路的平均可达速率Ru(h，f*) ∈R+最大化.毫米波下行链路可达速率定义为：

图2所示为图像预测最佳波束向量的神经网络模型，采用Faster RCNN 模型识别图像中用户坐标，流程图如图2Faster RCNN 模块所示：（1）首先将基站捕获的图像上传到MEC 服务器；（2）MEC 服务器将上传的图像输入到Faster RCNN 的主干网络提取特征得到特征图；（3）通过区域选取结构生成检测的候选框，将生成的候选框投影到特征图上获得相应的特征矩阵；（4）每个特征矩阵通过池化层缩放到7×7大小的特征图；（5）最后将特征图展平通过一系列全连接层得到预测结果和边界框回归参数，将预测边界框中心化输出为用户坐标.其中深度学习损失函数定义为：

图2 图像辅助毫米波波束预测流程图Fig.2 Image assisted millimeter wave beam prediction flowchart

其中Lcls（Lreg）表示针对用户分类和用户定位的损失函数.

图2DNN 网络模块所示为预测用户坐标与最佳波束向量的非线性关系，其中网络结构有两个主要部分，即基础网络和分类层.（1）基本网络：该网络包括4 层全连接层，每层都具有1024 个神经单元.每层全连接层采用ReLU 非线激活函数，并添加失活函数Dropout 防止模型过拟合.相比较文献［5］选取5 层全连接层，每层具有2048 个神经单元，本文所提出的网络架构复杂度显著降低.（2）分类层：本文选用Softmax 用来对基本网络层的输出进行分类.通过输出码本对应索引的概率分布P={p1，....，pB}，选取最大概率的元素作为波束向量索引，定义为：

为了使网络训练达到更好的拟合效果，本文对所预测用户坐标进行归一化预处理.采用离差标准化，使得用户坐标矩阵的值映射在［0，1］之间，这样不仅能够加快梯度下降求最优解的速度，同时能够提高训练精度.波束预测数据集标签构造，通过预测的用户坐标的独热编码向量与通过公式（6）穷举算法所得最佳波束成形向量的索引相对应来实现.数据集准备好之后，训练神经网络模型的损失函数最小化交叉熵定义为：

其中t=[t1，...，tD]是目标独热编码向量，pd代表神经网络预测的输入用户坐标属于dth的概率.

3 仿真分析

本文采用文献［14］的ViWi 数据集进行仿真实验，研究基于深度学习图像辅助波束预测方案的性能.该数据集是一个室外场景，其中包含RGB图像和mmWave信道，描述一辆汽车行驶在城市街道.在基站上配备毫米波天线和具有100°视野的摄像机.BS的高度设置为5 m（不考虑遮挡情况），汽车共有五个轨迹可直线行走，每个轨迹长100 m，并具有1000个等距点.通过labelImg 软件标注生成目标检测训练集和测试集，对于波束预测设定参数如表1.

表1 波束预测信道生成参数Tab.1 Beam prediction channel generation parameters

在本小节中，使用文献［14］数据集通过Faster RCNN 网络从图像中预测的用户坐标，研究基于用户坐标预测毫米波波束方案性能.以及评估mmWave天线阵列规模大小对预测性能的影响，并将文献［5］作为基线算法进行对比.

图3 表示在基站天线数为32，SNR=20 dB 时，不同数据集大小的情况下，参考文献［5］，选取Top-1和Top-3作为波束预测精度评判标准，其中x轴表示数据集大小的百分比，y轴表示模型预测准确率.Top-1 定义为预测概率最大的波束向量，Top-3 定义为预测概率前三的波束向量.由图3可见：当使用全部数据集进行训练时，Top-1 和Top-3 分别达到77%和99%，当训练集大小在40%时就十分接近理想状态.图4 表示在基站天线数32 时，不同SNR 情况下预测的Top-1 和Top-3 最佳波束向量通过公式（6）计算得到的可达速率.由图4 中可见，Top-1 的准确度已经可以接近理论上限可达速率.上述结果表明通过深度神经网络可以由用户坐标有效地预测毫米波波束向量.

图3 训练集大小对准确率的影响Fig. 3 Effect of training set size on accuracy

图4 信噪比对Top-1和Top-3可达速率的影响Fig. 4 Effect of SNR on Top-1 and Top-3 reachable rates

图5表示基站毫米波天线阵列数为4、16、32、64和128时，SNR 对Top-1评价标准下平均可达速率的影响.由图5 可见：小规模天线阵列的情况下（如天线阵列数为4时），Top-1可达数率几乎接近理论上限.随着天线阵列数量的增加，Top-1 可达速率性能出现下降，这是因为当天线数增加时，波束分类的数量也相应增加，导致分类的准确度下降，从而影响波束预测的性能.因此对于大规模天线阵列应适当增加计算复杂度，提高预测的准确性，如选取Top-3 作为评价标准，通过预测的三个波束向量选择可达速率最高的波束，作为天线阵列的最佳波束向量.图6表示在天线阵列数为64 和128 时，SNR 对Top-3 标准下可达速率的影响.对比图5 和图6 可知：与Top-1相比，Top-3的可达速率更接近理论上限.

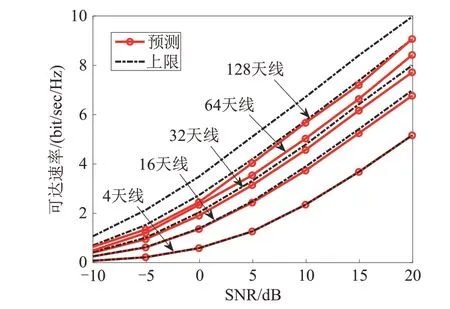
图5 天线阵列数为4、16、32、64、128时，信噪比对Top-1可达速率的影响Fig. 5 Effect of SNR on Top-1 reach rate with the number of antenna arrays of 4， 16， 32， 64， 128

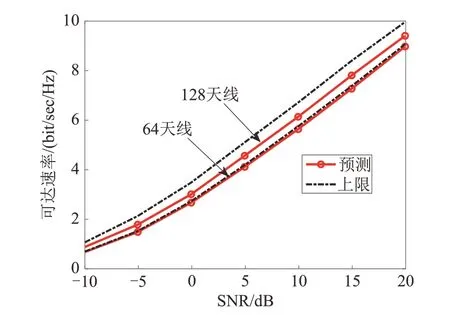
图6 天线阵列数为64、128时信噪比对Top-3可达速率的影响Fig. 6 Effect of SNR on the achievable rate of Top-3 with the number of antenna arrays of 64 and 128

由于码本和系统存在差异，为了更好和其它波束成形方案进行比较，本文选择可达速率差值，模型参数量和模型大小作为评判标准，其中可达速率差值定义为：

式中：R(hmmW，f)upper 为系统理论最优平均可达速率，R(hmmW，f*)pre为所提方案的平均可达速率.

图7表示不同天线阵列数量下不同模型参数量和大小的比较，x轴表示天线阵列数量，左y轴表示参数数量，右y轴表示参数大小.图7 中比较了本文方案和基线算法的复杂度.由图7 中可见：在16 天线数量下，基线算法模型参数数量相当于本文方法的8.2倍；在32天线数量下，本文方法的模型大小是基线算法的1/8 大小.这表明本文方法在复杂度方面远低于基线算法.

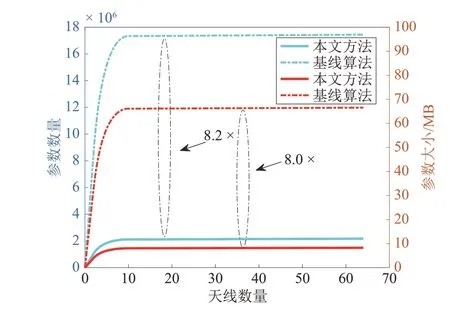
图7 不同天线下模型参数数量和大小的比较Fig. 7 Comparison of the number and size of model parameters under different antennas

表2所示为在不同规模天线阵列和SNR的情况下，本文所提方案和基线算法平均可达速率差值的比较结果.由表2 可见本文所提方案预测性能更接近系统最优.当天线数为64，SNR=-10 dB 时，本文所提方案的可达速率差值相比基线算法降低了98.76%.当天线数为64，SNR=20 dB 时，本文方案的可达速率差值相比基线算法降低了62.71%.仿真结果表明，本文的方案在大规模天线阵列和低信噪比的情况下性能更加优越.

表2 天线阵列数4、16和64时基于信噪比的平均可达速率差值Tab. 2 Average achievable rate difference based on SNR for antenna array numbers of 4 and 64

4 结语

本文首先提出采用Faster RCNN 模型检测通信环境中用户具体坐标，并通过用户坐标预测出最佳波束的思想.实验证明通信环境中用户图像与最佳波束向量的非线性关系能够通过深度神经网络学习来获得，基于图像辅助能够快速准确的进行毫米波波束预测，满足高速移动环境下毫米波的可靠性通信需求.仿真结果表明，采用本文方案的用户通信可达速率可以逼近系统理论上限.与文献［5］方案相比，在大规模天线阵列和低信噪比的情况下，本方案具有显著优势.未来可考虑将该方案应用于无人机地面通信应用场景，无人机通过捕获视觉数据，可用于识别地面终端的位置与分布，从而进行功率分配和位置追踪等.