带延时补偿的永磁同步电机自适应无差拍电流预测控制

何栋炜, 曾志伟, 蒋学程, 陈 炜, 刘丽桑, 陈 健

(1.福建理工大学 电子电气与物理学院,福建 福州 350118;2.闽江学院 物理与电子信息工程学院,福建 福州 350108)

0 引言

永磁同步电机(PMSM)具有优良的控制精度和较高的功率密度、转矩脉动小,被广泛用于数控机床、机器人和电动工具等智能制造装备[1-2]。电流环控制是决定永磁同步电机伺服系统性能的关键因素。永磁同步电机常用的电流控制方法有比例积分(Proportional Integral,PI)控制[3]。传统PI控制器的控制带宽存在理论极限的问题,动态响应无法进一步提升。预测控制具有高带宽、低电流谐波含量以及高动态性能等优点,能够满足永磁同步电机动稳态性能要求较高的场合。目前预测控制主要分为模型预测控制(Model Predictive Control, MPC)和无差拍预测控制(DPC)两种。DPC控制频率恒定、实现简单,更适用于要求高性能驱动的场合[4]。永磁同步电机是一个非线性时变的系统,其定子电阻、电感和永磁体磁链会随着电机运行工况的不同而变化。无差拍电流预测控制(DPCC)动稳态性能的关键在于电机参数的精度。电流环控制系统不仅受参数失配的影响,还存在采样、计算和脉宽调制(Pulse Width Modulation, PWM)更新延时。实际数字控制系统的延时是不可避免的,这种延迟将导致电流振荡,并极大地降低整个系统的控制性能[5]。

针对系统延时带来的影响,文献[6]采用现场可编程逻辑阵列来实现电流过采样,提升了电流环的采样精度,但是硬件编程工作量大。文献[7]中的两步预测是解决系统延时的常用方法。

针对参数失配引起电流跟踪性能下降的问题,文献[8]引入高增益扩张状态观测器实时观测系统扰动,将观测值作为电流前馈进行补偿。文献[9]引入非线性状态观测器来观测电流扰动,同时采用固定系数法简化设计过程,但需要调优的参数较多。文献[10]引入滑模观测器对参数失配引起的电流扰动进行补偿,但滑模算法固有的抖振问题未能有效消除。文献[11]提出新型模型参考自适应的参数分步辨识方法,解决了模型欠秩的问题,提高参数辨识精度,但设计过程较为复杂。文献[12]借鉴放松约束条件的思想改进DPCC算法,改进后的算法具有更广的电感适配范围,但仅考虑了电感失配的情况。

以上解决参数失配影响的方法是基于传统的电机模型,而增量式电机模型是基于非传统的电机模型,可以消除部分参数对控制算法性能的影响。文献[13]引入鲁棒因子和前馈控制改进了预测的电压方程,同时采用增量式电流静差消除算法消除了磁链对控制算法的影响,同时提高DPCC抵抗参数干扰的鲁棒性。文献[14]构建增量式预测电压方程,消除了定子电感和永磁体磁链对控制算法的影响,并对给定电压增量进行自适应补偿,减小预测电压误差。但是文献[13-14]未考虑到系统延时的综合影响。

针对上述控制方法的不足,本文提出一种带延时补偿的自适应无差拍电流预测控制算法。在考虑PMSM电流控制系统中存在的两个控制周期延时条件下,分析了实际数字控制系统的控制时序,并通过两步预测来补偿延时。在此基础上,通过仿射投影算法(Affine Projection Algorithm, APA)对简化后的q轴电流环模型参数进行估计,当仿射投影算法辨识收敛时经过改进的模型自适应补偿,将控制目标等效成无参数变化影响的标称系统。

1 传统无差拍电流预测控制

假设PMSM为对称结构,铁心磁路不饱和,铁损耗、涡流损耗都被忽略。在同步旋转(d-q)坐标系中,PMSM的电压方程可以表达为[15]

(1)

式中:ud、uq、id、iq分别为定子绕组的电压、电流在d-q轴的分量;Rs为定子电阻;Ld、Lq分别为电感在d-q轴的分量;ωe为转子的电角速度;ψf为永磁体磁链。

本文采用id=0的电流控制策略,在采样时间Ts足够小的情况下,可以认为id≈0(d轴电流采用传统PI控制方法)。式(1)采用一阶向前欧拉法[16],得到PMSM在k+1时刻的q轴离散模型如(2)所示:

iq(k+1)=(1-RsTs/Lq)iq(k)+

(Ts/Lq)uq(k)-ψf/Lqωe(k)

(2)

式中:Ts为电流控制器的采样时间;k表示第k个采样时刻;ωe(k)为k时刻的电角速度;iq(k)为k时刻定子电流采样值在q轴的分量。

在实际的数字控制系统中,电流采样、电压计算和PWM更新不在同一时刻,计算得到的电压无法在当前时刻得到执行,而是在下一个采样时刻执行并加载到逆变器上,导致PMSM电流响应存在两个控制周期延时。其电流环的控制时序如图1所示[17]。

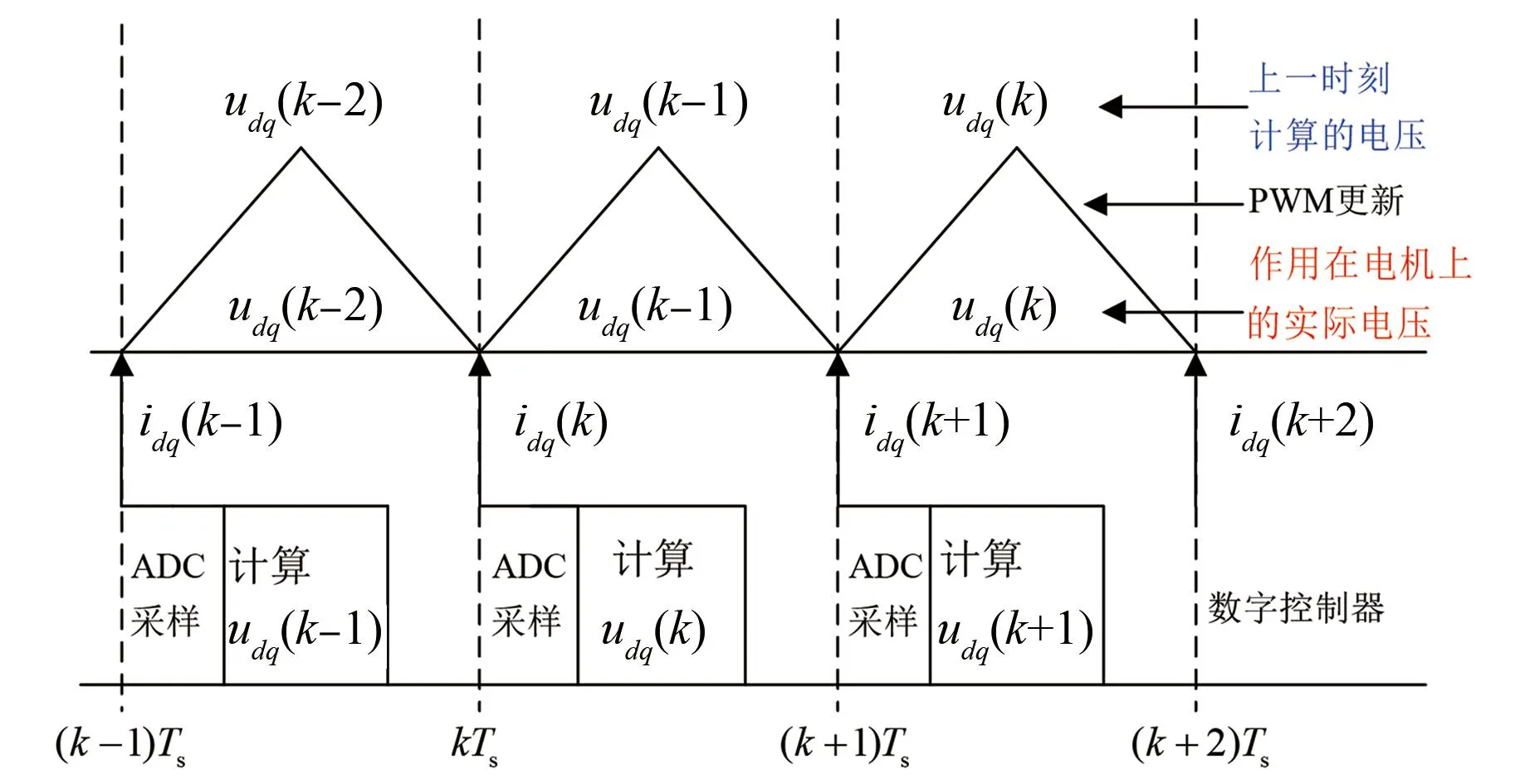
图1 电流环控制时序图Fig.1 Timing diagram of current control

在实际数字电流控制系统中,k时刻计算得到的控制指令电压uq(k)在k+1时刻到k+2时刻作用在电机上产生k+2时刻的采样电流iq(k+2)。考虑到采样频率较高,转速变化相较电流变化慢很多,因此有ωe(k+1)≈ωe(k)。则式(2)可以改写为

iq(k+2)=αiq(k+1)+βuq(k)-γωe(k)

(3)

式中:α、β、γ为离散化的电机模型参数值,α=1-RsTs/Lq、β=Ts/Lq、γ=ψfTs/Lq;uq(k)为k时刻的q轴计算电压。

同理,k+1时刻q轴电流离散模型可以表示为

iq(k+1)=αiq(k)+βuq(k-1)-γωe(k)

(4)

式中:uq(k-1)为k-1时刻的q轴计算电压。

为使iq(k+2)能够跟踪上k时刻的给定电流,根据文献[17]可以得出k时刻的DPCC计算电压:

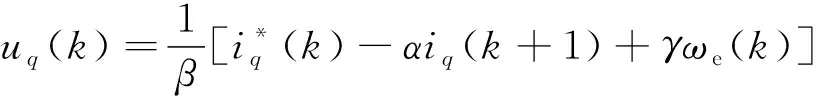
(5)

综上所述,由式(4)和式(5)构成的无差拍电流预测控制可以改善实际数字控制系统中存在的控制延时对电流环的影响,但该方法对参数的准确性敏感度较高[17]。而电机实际参数往往无法准确获得,并且在实际运行中,电机的定子电阻Rs、电感Ldq和永磁体磁链ψf会随着运行环境的变化而变化,因此参数失配会不可避免地影响传统无差拍电流预测控制器的控制效果,甚至影响电流环的鲁棒性。因此,需要针对此不足进行改进,才能进一步提高电流环的控制性能。

2 带延时补偿的永磁同步电机自适应无差拍电流预测控制

针对PMSM参数失配对电流跟踪性能的影响,本文在考虑控制延时的q轴电流控制模型基础上,引入仿射投影算法,设计带延时补偿的永磁同步电机自适应无差拍电流预测控制。

本文所设计的带延时补偿的永磁同步电机自适应无差拍电流预测控制算法结构如图2所示。

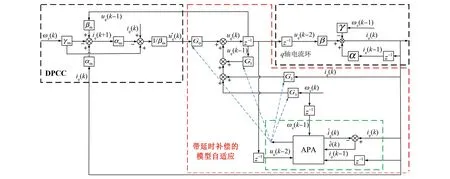
图2 带延时补偿的永磁同步电机自适应无差拍电流预测控制算法结构Fig.2 Structure of adaptive deadbeat current predictive control algorithm for permanent magnet synchronous motor with delay compensation

图中,红色虚线框内是基于仿射投影算法的改进模型自适应补偿,内部包含的绿色虚线框是考虑延时的q轴电流环模型的仿射投影算法,用来实现模型参数的辨识,详细设计过程详见下一节。黑色虚线框内分别是q轴的无差拍电流预测控制器(DPCC)和考虑两个周期延时的被控对象(q轴电流环),蓝色虚线指向的是模型自适应补偿算法中的补偿函数。

2.1 带延时补偿的模型自适应补偿

带延时补偿的模型自适应补偿具体设计如下。无差拍电流预测控制器由式(5)整理可得:

(6)

式中:Rm、Lm、ψfm为电机铭牌上获得的标称参数;αm、βm、γm分别为1-RmTs/Lm、Ts/Lm、ψfmTs/Lm。在实际运行过程中,电机参数存在偏差,因此电机实际离散模型参数α、β、γ与标称αm、βm、γm之间存在偏差,显然会影响无差拍电流预测的控制效果。

在当前k时刻,可以采样获得iq(k),且记录有ωe(k-1)和uq(k-2)。由上节及式(4),易得k时刻q轴电流离散模型为

iq(k)=αiq(k-1)+βuq(k-2)-γωe(k-1)

(7)

式中:uq(k-2)为k-2时刻的q轴计算电压。

以实际电机输出的信号iq(k)作为参考输出信号,基于仿射投影算法,以式(7)作为参数辨识模型设计在线估计算法(设计过程详见下节)。当仿射投影算法收敛时,显然下式成立:

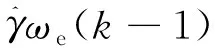
(8)

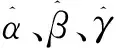
当仿射投影算法估计值收敛时,由式(8)可递推出k+1时刻的q轴估计电流满足:

(9)

同理,可以推导出k+2时刻的q轴估计电流满足:

An examination of the self-adaption algorithms used in qualitative precipitation estimations

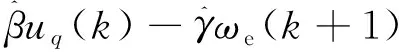
(10)

考虑ωe(k+1)≈ωe(k),将式(9)代入式(10),则k+2时刻的q轴估计电流可以表示为

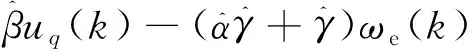
(11)

同理,可以得到系统标称模型为

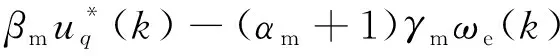
(12)

式中:αm、βm、γm为电机标称参数。

以标称模型为补偿目标,带延时补偿的模型自适应控制器如图2所示,设计为

G2iq(k)+G3ωe(k)

(13)

将式(13)代入式(11)化简可得:

(14)

为实现对参数失配的影响,自适应补偿后,式(14)应与标称模型式(12)等效,因此有:

(αm+1)γmωe(k)

(15)

为了使式(15)成立,则图2所示的补偿传递函数设计为

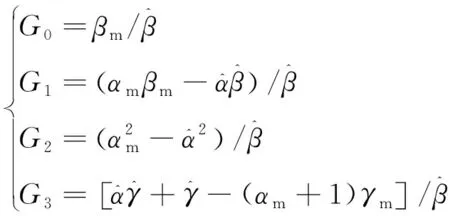
(16)

综上可知,在所设计控制器作用下,k+2时刻的控制目标可以等效成无参数变化影响的标称模型的充分条件为满足式(8)、(9)、(10)和(16)成立。

2.2 仿射投影算法

为了保证补偿性能,本文引入仿射投影算法设计辨识器,保证式(8)成立。以k时刻采样电流iq(k)作为参考输出信号,基于式(8)建立参数辨识模型,设计q轴电流环仿射投影算法结构[18],如图3所示。图中e(k)为辨识模型与实际电机系统的输出误差。

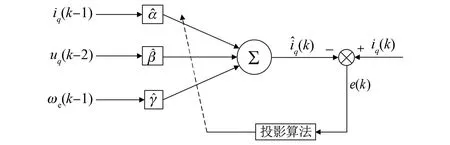
图3 q轴电流环仿射投影算法结构图Fig.3 Structure of q-axis current loop affine projection algorithm

根据仿射投影算法的原理,其最小化的无约束函数为[18]

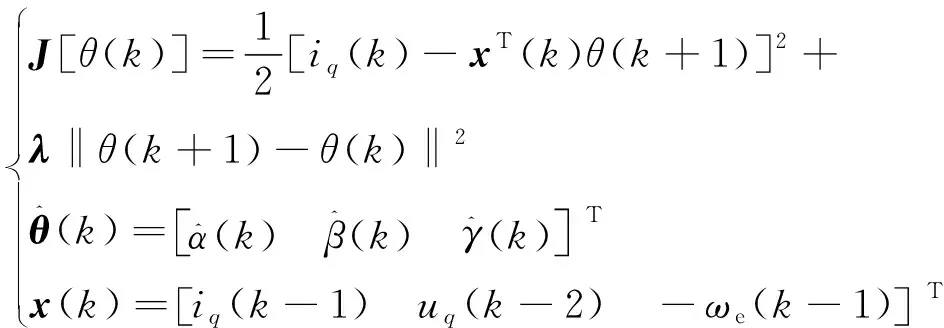
(17)

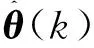
为使下一个估计参数向量尽可能与当前估计参数向量保持接近,并强迫后验误差为零。令J[θ(k)]相对于θ(k)的梯度为零,引入收敛因子μ,取得最终失调与收敛速度之间的平衡,同时引入计算相关矩阵的调整参数ζ,避免矩阵求逆过程中的数值问题[18]。新的估计参数更新方程为

(18)

3 仿真结果及分析

为了验证本文所提出控制方法的可行性及性能,在MATLAB/Simulink平台上搭建仿真模型进行验证,仿真选取文献[21]中基于二阶超螺旋滑模观测器(Super Twisting Sliding Mode Observer,STSMO)的改进无差拍电流预测控制算法进行对比(文献[21]与本文中的研究对象原理相同,结构略有区别,因此控制方法通用),以验证本文方法的性能。文献[21]中所设计的控制算法结构如图4所示。

图4 基于二阶STSMO的改进PCC控制结构图Fig.4 Structure diagram of improved PCC control based on second-order STSMO

如图4所示,文献[21]中的控制算法应用于本文所用的被控对象。图中,红色虚线框内是基于二阶STSMO的q轴PCC,文献[21]中方法使用二阶STSMO对扰动及q轴电流分别进行估计和预估,并利用估算结果进行输出电压补偿,而本文则使用仿射投影辨识和补偿函数来实现补偿;黑色虚线框内是考虑延时的被控对象(q轴电流环),与文献[21]中应用对象一致(变量符号有调整)。

模型为速度环采用PI控制的双闭环控制系统,速度环在电机起动以及电机稳定于高速运行时给电流环一个阶跃给定,以测试电机在空载和加载不同运行情况下的参数失配对q轴电流环控制器的影响。测试过程设计为:电机以额定转速3 000 r/min从空载起动到稳定运行,主要考察电流环在空载调整阶段的动态响应性能和空载稳定阶段的电流稳态跟踪性;在0.3 s时突加0.2 N·m的负载转矩,0.4 s时负载突减为0 N·m至0.5 s仿真结束,主要考察电流环在加载阶段的动态响应性能和稳态跟踪性能。仿真中采样频率为20 kHz,q轴给定电流限幅iq max=2.5 A,电压限幅为uq max=48 V。电机的标称参数为:αm=0.96 (Ω·s)/H,βm=0.029 44 s/H,γm=0.000 33 (Wb·s)/H。二阶超螺旋滑模观测器的增益选取k1=2 000、k2=500 000。仿射投影算法的参数选取μ=0.4、ζ=0.000 001。仿真中使用的PMSM参数如表1所示。

表1 电机参数Tab.1 Motor parameters

为了对比分析不同参数偏差下两种方法的补偿效果,将参数失配的情况分为典型的8种,分别为(1)Rm=2Rs,(2)Lm=2Ls,(3)ψfm=2ψf,(4)Rm=2Rs、Lm=2Ls,(5)Lm=2Ls、ψfm=2ψf,(6)Rm=2Rs、ψfm=2ψf,(7)Rm=2Rs、Lm=2Ls、ψfm=2ψf和(8)Rm=0.5Rs、Lm=0.5Ls、ψfm=0.5ψf,对不同程度的参数失配情况进行综合分析[11-21]。为保证仿真结果的可对比性,仿真中保持电机本体的参数不变,通过改变电流环控制器中的标称参数Rm、Lm和ψfm模拟电机实际运行时的参数失配。

此外,文中使用标准差来评估两种控制方法在稳态阶段的q轴电流脉动,其表达式为

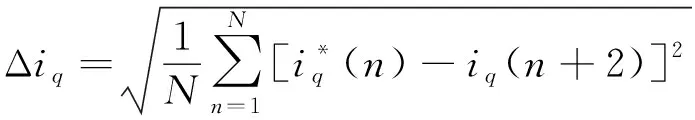
(19)

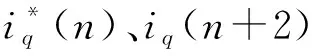
以电流控制器中的标称参数Rm、Lm和ψfm分别是电机实际参数Rs、Lq和ψf的2倍为例,对比如下。基于二阶STSMO的PCC与本文所设计方法的转速波形对比如图5所示。

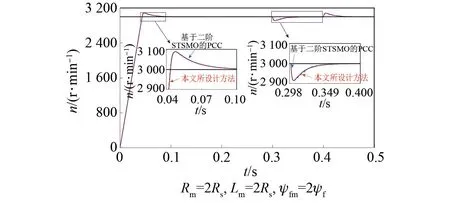
图5 两种控制方法的转速波形对比Fig.5 Comparison of the speed waveforms of the two control methods

从图5可以看出,两种控制方法仿真的转速均能够在0.1 s左右达到额定转速且稳定在3 000 r/min;在0.3 s时突加0.2 N·m的负载转矩,0.4 s时负载转矩突减至0 N·m,这个阶段两种控制方法的转速均在85 r/min内波动,在0.38 s后稳定在3 000 r/min,二者速度变换情况接近。因此,可以看出两个电流环测试的转速基本一致。

在上述运行工况下,两种控制方法在空载调节阶段的电流跟踪效果、q轴电流误差对比以及q轴电压波形对比如图6、图7和图8所示。

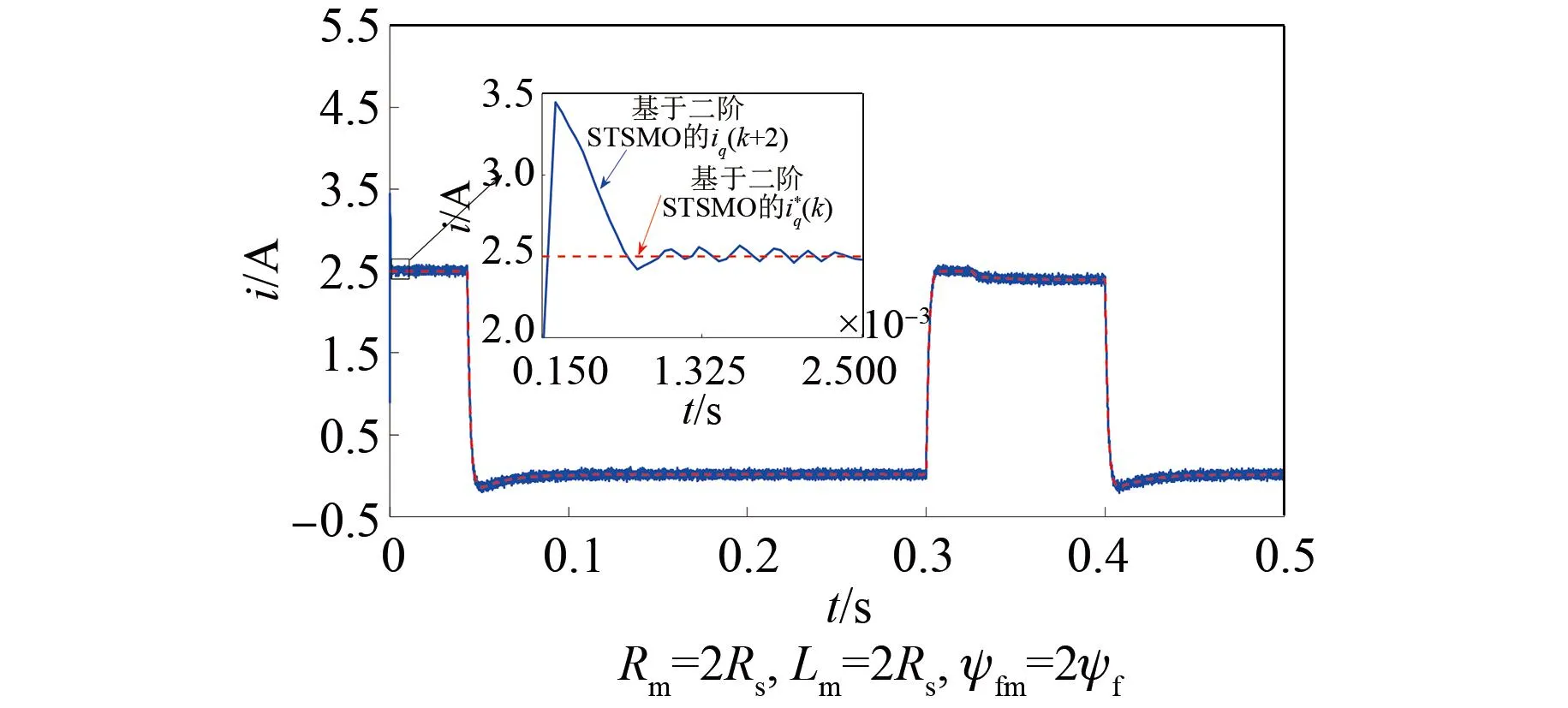
图6 基于二阶STSMO的PCC在空载调节阶段的电流跟踪效果Fig.6 PCC current tracking performance based on second-order STSMO in the no-load regulation stage

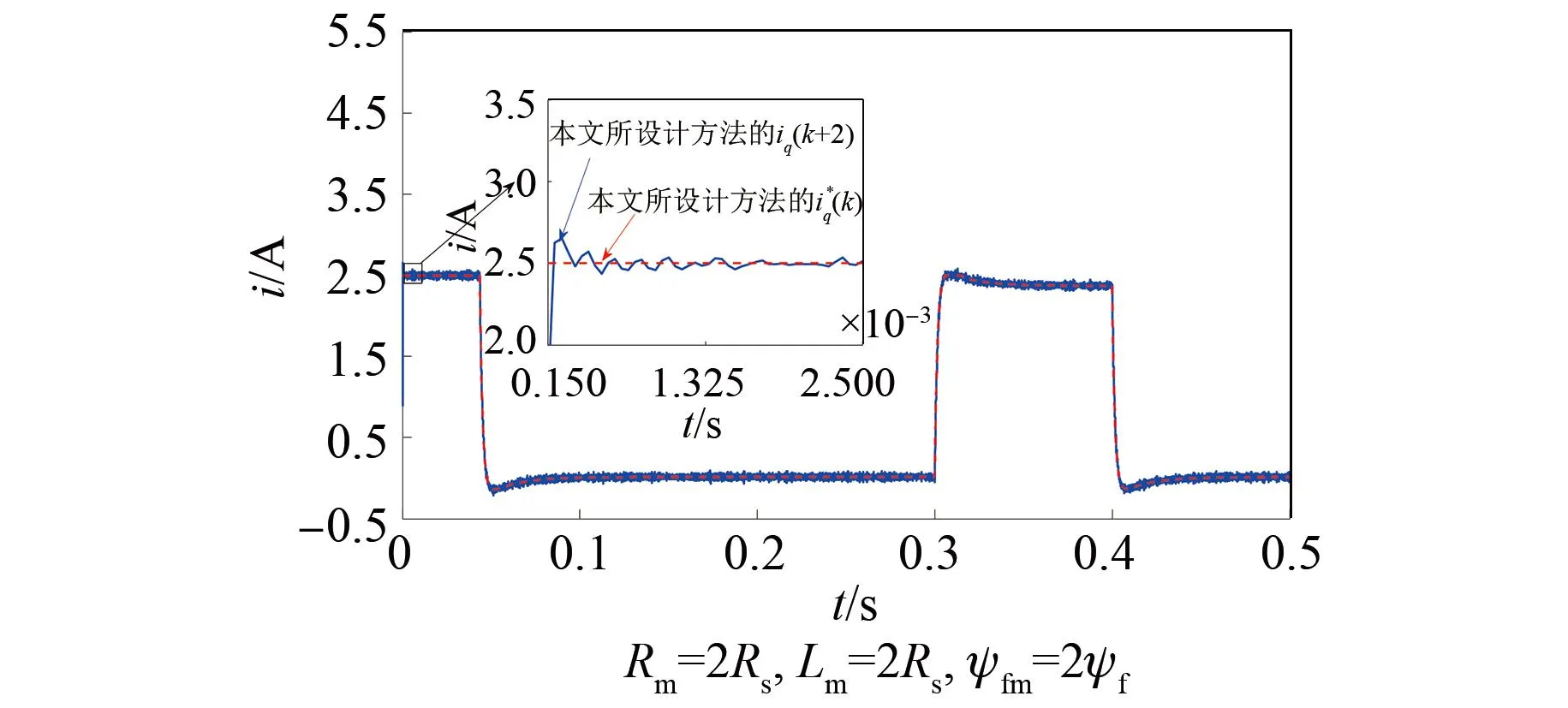
图7 本文所设计方法在空载调节阶段的电流跟踪效果Fig.7 Current tracking performance by the design method in this paper in the no-load regulation stage

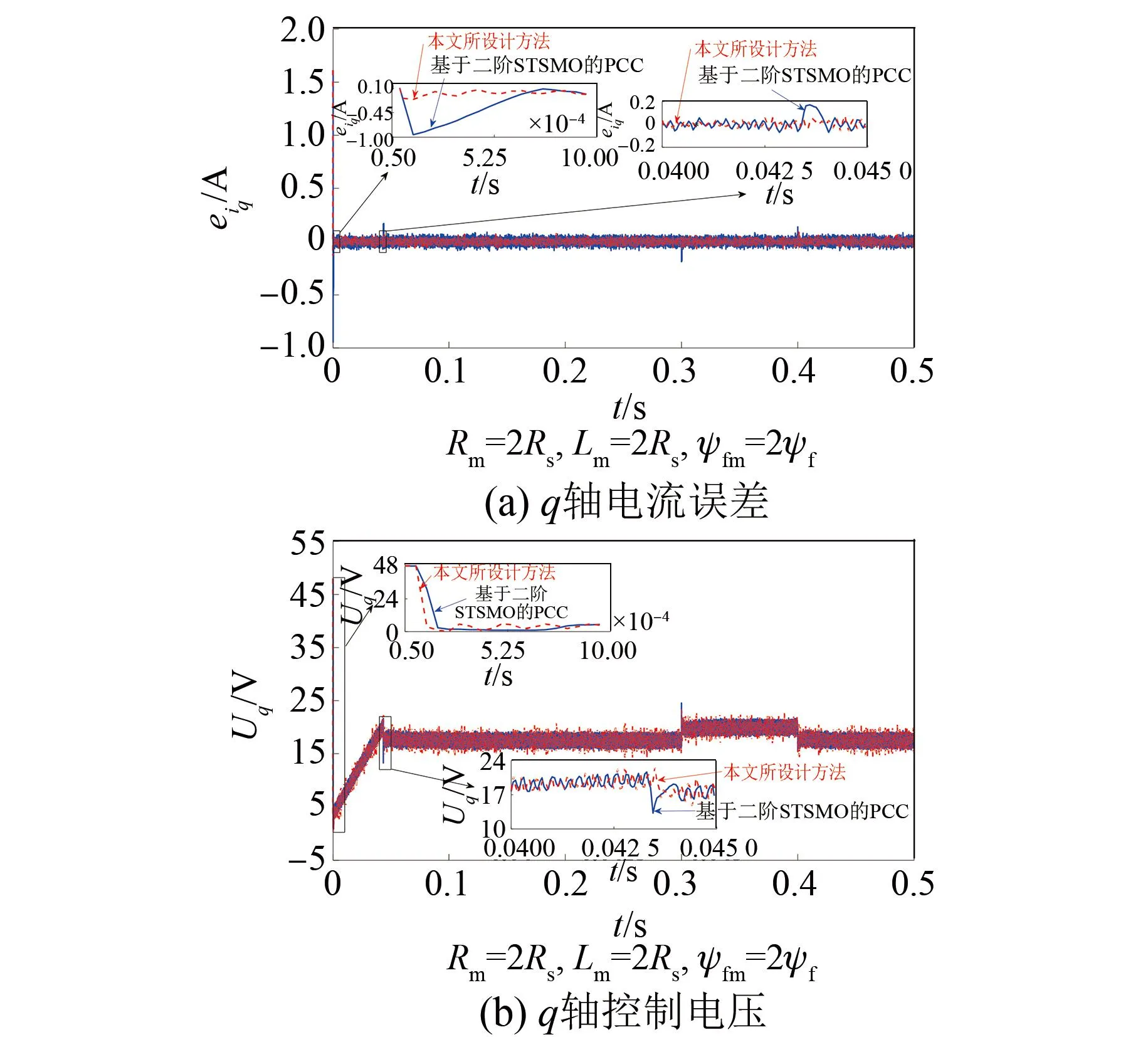
图8 两种控制方法在空载调节阶段的q轴电流误差及控制电压对比Fig.8 Comparison of q-axis current errors and control voltage between the two control methods in the no-load regulation stage

空载起动阶段,由图6和图7中0.000 15 s到0.002 5 s的放大图可以看出,本文所设计方法的iq调节时间约为0.000 5 s,超调量约为6.06%;而基于二阶STSMO的PCC的iq调节时间约为0.001 s,超调量约为37.83%。由图8(a)中0.000 05 s到0.001 s和0.04 s到0.045 s的放大图可以看出,本文所设计方法的q轴电流跟踪误差一直稳定在±0.08 A。特别是0.043 s处q轴电流给定值突变时,基于二阶STSMO的PCC的q轴电流跟踪误差在0.043 s处扩大为-0.07～0.17 A,在0.044 s后稳定在±0.08 A。由图8(b)中0.000 05 s到0.001 s和0.04 s到0.045 s的放大图进一步可知,与基于二阶STSMO的PCC相比,本文所设计方法的q轴控制电压稳定速度快且在0.04 s到0.045 s阶段变化平滑。由此表明,电压与电流存在因果关系,控制电压的变化影响着电流跟踪性能。由上述对比可知,电机电流起动至0.045 s左右是空载情况下的电流调整阶段,该阶段电机以低速运行状态为主,其反电动势耦合影响较小,q轴电流阶跃响应主要受到电阻误差和电感误差的影响。相比二阶STSMO的PCC,本文所设计方法的q轴控制电压稳定收敛速度快,电流跟踪收敛速度较快,并且超调量较小,说明本文所设计方法在空载情况下能够更快地补偿电阻误差和电感误差带来的影响,具有较好的动态响应性能。

空载稳定阶段,基于二阶STSMO的PCC与本文所设计方法的电流跟踪效果、q轴电流误差对比以及q轴电压波形对比如图9、图10和图11所示,其主要体现空载情况下电流稳定阶段的电流稳态响应性能。

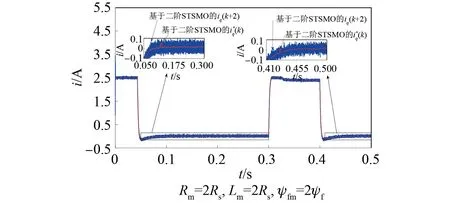
图9 基于二阶STSMO的PCC在空载稳定阶段的电流跟踪效果Fig.9 PCC current tracking performance based on second-order STSMO in the no-load stable stage

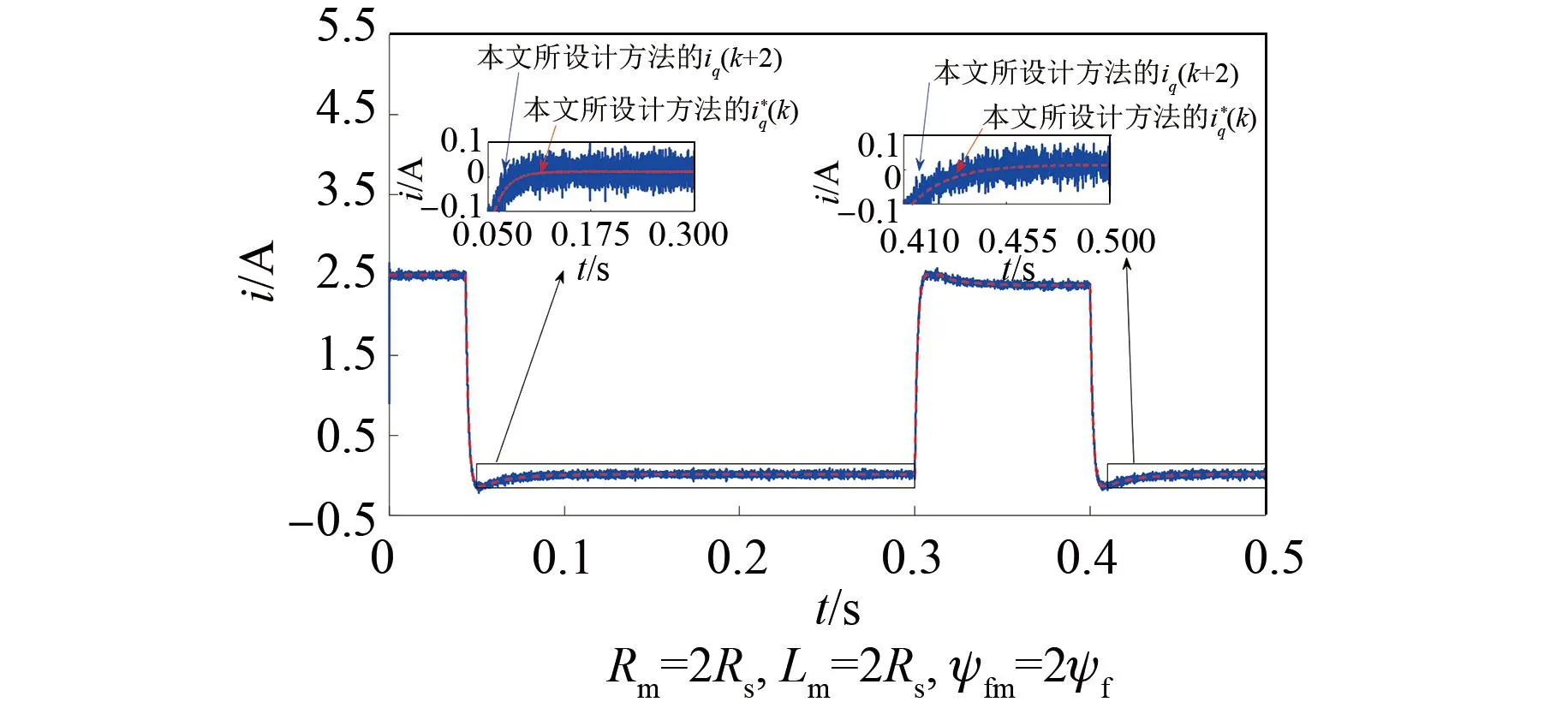
图10 本文所设计方法在空载稳定阶段的电流跟踪效果Fig.10 Current tracking performance by the method designed in this paper in the no-load stable stage

图11 两种控制方法在空载稳定阶段的q轴电流误差及控制电压对比Fig.11 Comparison of q-axis current error and control voltage of the two control methods in the no-load stable stage

由图9和图10中0.05 s到0.3 s和0.41 s到0.5 s的放大图可以看出,基于二阶STSMO的PCC的iq在±0.1 A内波动(q轴电流脉动的标准差为30.7 mA);本文所设计方法的iq在±0.08 A内波动(q轴电流脉动的标准差为24 mA)。由图11(a)和(b)中0.05 s到0.3 s和0.41 s到0.5 s的放大图可以看出,本文所设计方法在空载情况下电流稳定阶段的q轴控制电压变化较快,q轴电流跟踪误差在±0.08 A,而基于二阶STSMO的PCC的q轴电流跟踪误差在±0.09 A。由此表明本文所设计方法的q轴控制电压在空载情况下电流稳定阶段调节速度较快,使得电流波动得到更好的抑制。由上述对比可知,电机在高速运行阶段,q轴电流响应受磁链参数失配影响为主,与基于二阶STSMO的PCC相比,本文所设计方法能够有效克服电机在高速运行情况下参数失配带来的影响,跟踪性能及稳定性能得到了改善,具有较好的鲁棒性。

负载突变阶段,测试中在0.3 s时突加0.2 N·m的负载转矩并且在0.4 s时负载转矩突减至0 N·m。基于二阶STSMO的PCC与本文所设计方法在加载阶段的电流跟踪效果、q轴电流误差对比以及q轴电压波形对比如图12、图13和图14所示,显然电流环在高速运行阶段完成了对变化电流的跟踪。

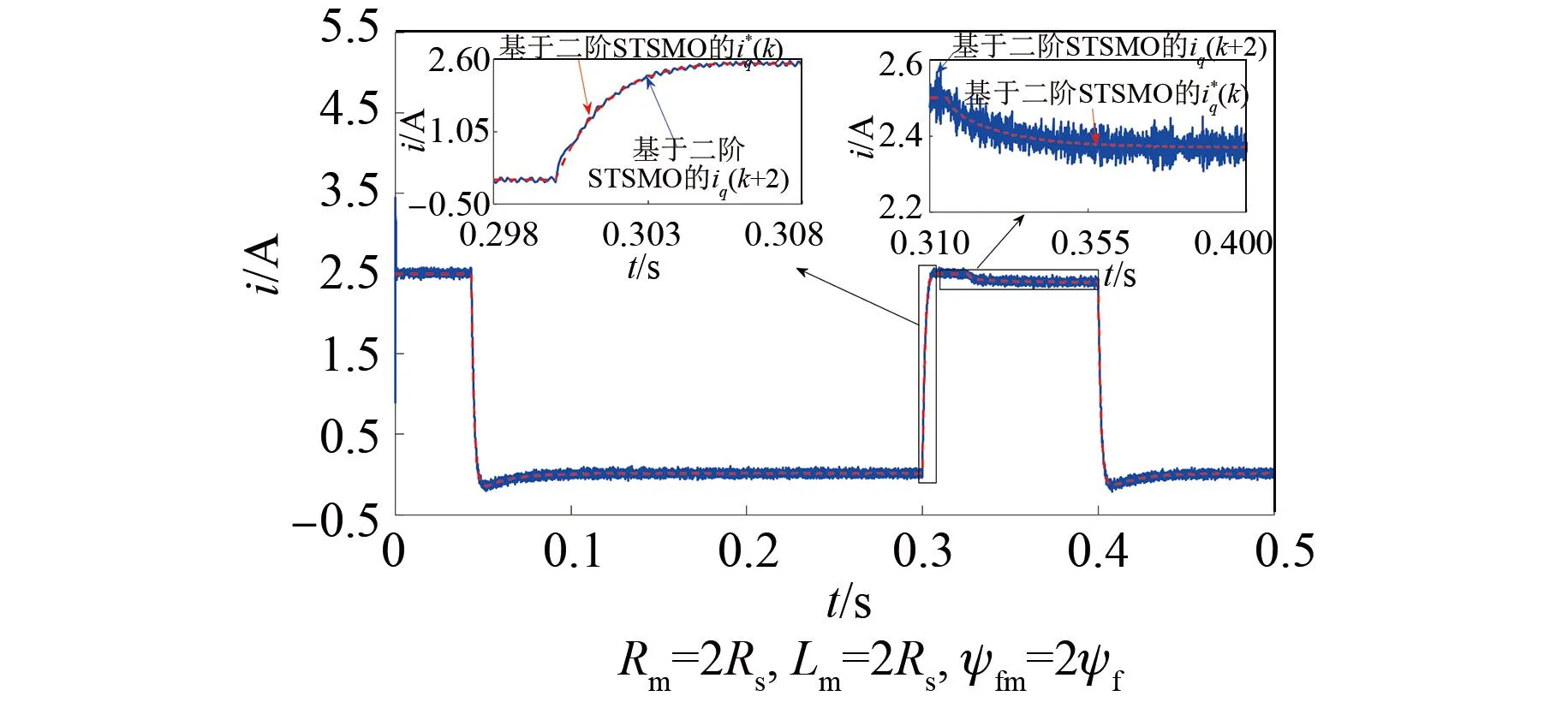
图12 基于二阶STSMO的PCC在加载阶段的电流跟踪效果Fig.12 PCC current tracking performance based on second-order STSMO in the loading stage

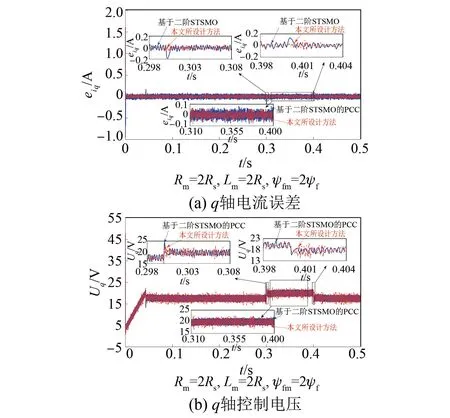
图14 两种控制方法在加载阶段的q轴电流误差及控制电压对比Fig.14 Comparison of q-axis current error and control voltage of the two control methods in the loading stage

由图12和图13中0.298 s到0.308 s和0.31 s到0.4 s的放大图可以看出,两种控制方法下的电流均能较好地响应给定电流变化。进一步,由图14(a)中0.298 s到0.308 s和0.398 s到0.404 s的放大图可以看出,基于二阶STSMO的PCC在加载情况下的电流调节阶段,q轴电流误差明显变大,0.300 4 s处的q轴电流误差扩大为-0.19～0.06 A,0.4 s处的q轴电流误差扩大为-0.06～0.14 A,而本文所设计方法的q轴电流误差能够稳定在-0.08～0.06 A。由图14(b)中0.298 s到0.308 s和0.398 s到0.404 s的放大图可以看出,与基于二阶STSMO的PCC相比,本文所设计方法q轴控制电压变化较快且平滑。由此表明,本文设计方法在0.298 s到0.308 s和0.398 s到0.404 s的q轴控制电压变化快且平滑,使得电流在给定电流变化时仍旧保持较好的动态响应性能,电流跟踪误差小。由上述对比分析可知,电机在高速运行阶段,q轴电流阶跃响应主要受到反电动势影响,本文所设计方法在参数辨识基础上进行在线补偿的反应速度及准确性优于对比方法,电流跟踪误差收敛速度较快。

由图14(a)中0.31 s到0.4 s的放大图分析加载情况下的电流稳定阶段电流跟踪性能,基于二阶STSMO的PCC的q轴电流跟踪误差在±0.08 A(q轴电流脉动的标准差为28.8 mA),本文所设计方法的q轴电流跟踪误差在±0.06 A(q轴电流脉动的标准差为22.8 mA)。由图14(b)中的0.31 s到0.4 s放大图可以看出,本文所设计方法的q轴控制电压变化较快。由此表明本文所设计方法的q轴控制电压变化较快,使得电流跟踪能够更好地抑制负载转矩和参数失配产生的电流波动。由上述对比可知,与基于二阶STSMO的PCC相比,本文所设计方法在高速及大电流情况下能够有效减小参数失配带来的稳态误差,具有较好的鲁棒性。

图15 q轴参数估计值和模型跟踪误差曲线Fig.15 The curve of q-axis parameter estimation and the tracking error

为充分验证本文所设计方法的可行性,除上述参数失配情况外,还测试了不同参数失配程度下的电流动稳态响应性能,如表2所示,表中的(1)～(8)与前文描述的参数失配情况一致。

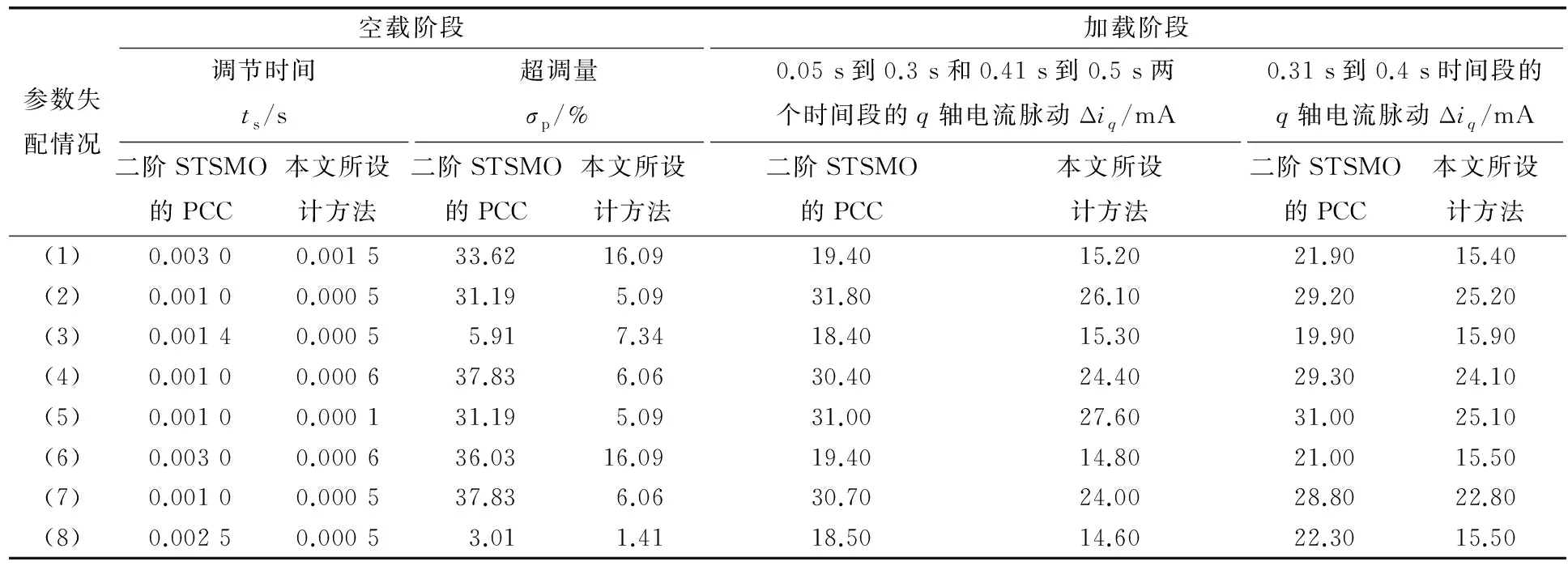
表2 两种控制算法在空载和加载阶段参数失配的情况下q轴电流性能对比Tab.2 Comparison of q-axis current performance of two control algorithms in the case of parameter mismatch in no-load and loading stages

表2中详细对比了两种控制方法在空载阶段和加载阶段的动态响应性能及电流跟踪性能。与基于二阶STSMO的PCC相比,本文所设计方法的q轴电流的调节时间短,超调小,在0.05 s到0.3 s、0.31 s到0.4 s和0.41 s到0.5 s这三个时间段的q轴电流脉动小。由此表明,电机在各种情况及不同参数失配运行下,本文所设计方法都具有自适应补偿能力更好的电流跟踪效果。

4 结语

本文针对电流跟踪控制性能受永磁同步电机数字控制系统存在的固有延时影响的问题,在传统无差拍电流预测控制方法基础上,为解决参数失配引起的电流控制性能下降的问题,提出一种具有滞后补偿模型的自适应无差拍电流预测控制方法。通过仿射投影算法对考虑控制延时的q轴电流环进行辨识并设计补偿器,依据参数估计值进行实时控制补偿,使受参数失配影响的q轴电流环等效成无参数变化影响的标称系统。仿真结果表明,相比基于二阶STSMO的PCC方法,本文所设计方法在各种参数失配情况下均能够有效改善电流环动态响应性能,减小电流跟踪的稳态误差,增强了系统的鲁棒性。