基于微分平坦的高超声速飞行器跟踪控制方法

赵昱宇, 索 超, 王雨潇

(中国民航大学电子信息与自动化学院, 天津 300300)

0 引 言

然而,高超声速飞行器模型具有强不确定性,反馈线性化等方法的过度模型依赖会导致系统鲁棒性下降。自抗扰控制(active disturbance rejection control,ADRC)利用扩张状态观测器(extended state observer,ESO)估计系统总扰动,并利用非线性反馈控制律进行扰动补偿。由于其弱模型依赖、鲁棒性强等特点,ADRC在不确定系统的控制设计中得到了广泛的应用[11]。文献[11]利用ADRC的无模型信息特性提高了分布式电源逆变器的鲁棒性。文献[12]将反步法结合ADRC实现了不确定分数阶系统的跟踪控制。特别地,针对飞行器控制问题,文献[13]提出一种改进ADRC控制方法,实现了小型无人直升机姿态控制。进一步地,文献[14]对ADRC方法进行了性能分析,通过提出疲劳度的概念验证了ADRC的性能优越性。文献[15]在ADRC基础上应用了前馈控制,实现了飞行器高度的快速调节,其中所提出的稳定裕度测试子对于ADRC频域稳定性分析具有较大的理论指导意义,可以实现参数的快速整定。但在高超声速飞行器的轨迹跟踪控制问题中,系统阶数较高,需要使用高阶ESO来观测系统状态或构建串级ADRC来分别实现内外环控制[16-17],其控制性能与广泛应用的二阶ADRC姿控系统具有一定的差距。此外,高超声速飞行器飞行走廊较为狭窄,需要在控制过程中考虑状态和控制输入等多约束问题[18],飞行状态的越界可能带来系统失稳或发动机熄火等问题[19]。因此,需要一种综合控制方法来实现多约束下的高超声速飞行器稳定轨迹跟踪。

微分平坦[20]在处理非线性系统问题上具有计算量小、计算效率高等特点[21-22]。由于微分平坦可以实现状态和控制输入到平坦输出的映射,因此在处理带有状态约束等控制和规划问题上具有优势。文献[23]基于微分平坦理论,结合样条函数等参数化平坦输出,实现姿态机动可行路径的快速规划。文献[24]采用全局插值多项式参数化平坦输出函数完成参考轨迹优化,并设计比例-微分(proportional-derivative, PD)控制律实现了多约束条件下高超声速飞行器的轨迹稳定跟踪。但微分平坦计算过程依赖精确的模型推导,且产生高阶微分信号,因此高相对阶和不确定模型应用微分平坦时的抗干扰性能和鲁棒性较差。

综上所述,对于高超声速飞行器轨迹跟踪控制问题,存在多约束条件、系统控制相对阶、气动参数不确定性强等特点。因此,考虑利用微分平坦对速度、高度动态进行微分映射,高度通道保留俯仰角作为中间控制量,而利用ADRC完成姿态跟踪。微分平坦所得到的平坦映射可以在平坦输出上反映系统过程状态信息,实现考虑过程约束的参考轨迹优化降维,姿控系统的保留使得推导相对阶数减小,不会产生高阶微分信号导致鲁棒性变差,也不会过度依赖不确定性较强的气动参数信息。而ADRC在姿控系统上的应用不需要处理俯仰角-高度动态,仅需设计二阶ESO,跟踪效果及鲁棒性较好。通过高超声速飞行器纵向轨迹跟踪仿真对所提出方法与现有方法的性能进行了比较,验证了基于微分平坦的高超声速飞行器跟踪控制方法的有效性。

1 模型描述

研究对象为有翼锥形体高超声速飞行器,其纵向动力学模型描述如下[25]:

(1)

系统有5个状态[V,r,γ,θ,q]T,和2个控制量[Φ,δe]T。其中V为速度,r为地心距(r=R+h,其中R为地球半径,h为高度),γ为弹道倾角,θ为俯仰角,q为俯仰角速率,Φ为燃油节流率,δe为升降舵。

推力T,阻力D, 升力L,俯仰力矩Myy拟合如下所示:

(2)

式中:相关的气动系数表达式为

(3)

(4)

(5)

CM=CM,α(α)+CM,δe(α,δe)+CM,q(q,α)

(6)

(7)

CM,δe(α,δe)=ce(δe-α)

(8)

(9)

2 基于微分平坦的控制系统设计

2.1 理论介绍

微分平坦理论是针对非线性系统所提出的一种线性化理论。其内容为,若存在至少一组平坦输出,使得非线性模型可以被线性化,即非线性系统中的所有状态和控制输入变量都能够由这组平坦输出及其有限阶微分表达,那么称该系统是微分平坦的[26]。

微分平坦理论是将非线性动态方程中的非线性特性分离出来,将动态非线性系统映射为非线性静态方程和线性动态方程的组合,从而实现非线性系统的线性化,示意图如图1所示。

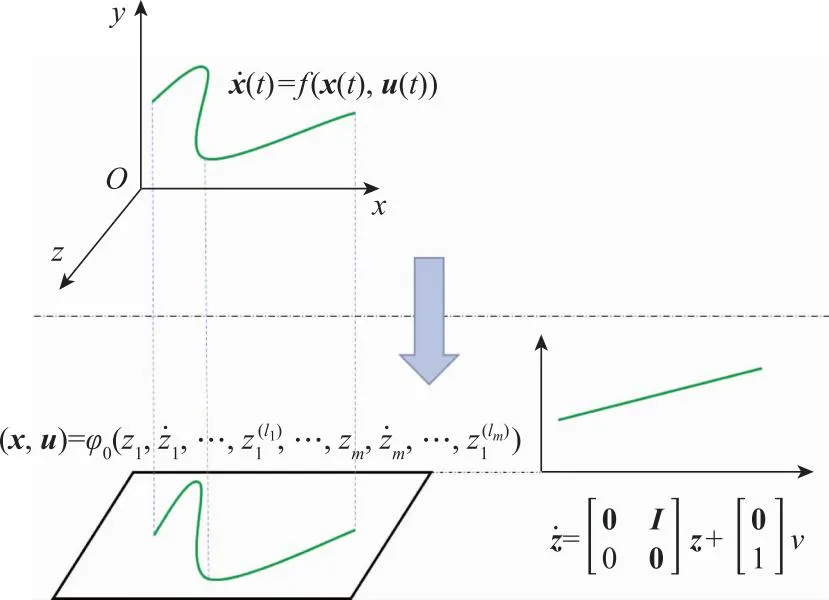
图1 微分平坦理论映射示意图Fig.1 Mapping diagram of differential flatness theory

若非线性系统

(10)

是微分平坦的,那么存在一组输出z∈Rm满足

zi=hi(x,u,…,u(ri)),i=1,2,…,m

(11)

使得系统的状态、控制输入和原输出都可以用输出z及其有限阶导数表示,即

(12)

式中:x∈Rn为状态变量,u∈Rm为控制输入;f(·)、h(·)为连续光滑函数。

因此,若系统是微分平坦的,则可以通过规划的期望平坦输出得到标称条件下所有状态及控制输入理想值。对于高超声速飞行器具有状态约束、控制输入约束的控制对象,微分平坦可以将输出轨迹信息映射到状态和输入上,以此解决带有约束的输出轨迹优化及跟踪控制问题。

2.2 平坦输出规划与跟踪控制

一般情况下,高超声速飞行器具有较为狭窄的飞行走廊,通常设计控制器时需要考虑动力学方程、状态与控制输入物理限制等多重约束条件,确定一条从初始状态到期望终端状态的控制轨迹,使得控制过程中系统满足约束条件,并达到期望性能指标,其数学描述如问题1 所示。

问题 1针对动态方程组,寻找状态变量-控制变量函数组{x(t),u(t)}(t∈[t0,tf])使得性能指标满足:

(13)

同时满足边界条件、控制饱和约束:

|u(t)|≤umax

(14)

|x(t)|≤xmax

(15)

式中:x(t)为状态变量;u(t)为控制变量;L(*)为性能指标计算函数;J*为期望性能指标。问题1包含对于微分方程的状态约束,规划空间维数较高,求解难度较大。

利用第2.1节微分平坦理论可将系统状态、控制输入等映射为平坦输出,一方面可以实现系统状态与控制约束到平坦输出约束的降维转化,另一方面可实现系统线性化,以进行跟踪控制系统设计。

由于姿控子系统存在较大不确定性,而微分平坦需要系统精确模型推导,因此高度回路仅将俯仰角-高度动态进行微分平坦变换,姿态跟踪利用ADRC实现,以此增强系统鲁棒性并避免微分推导爆炸问题。控制系统总结构框图如图2所示。

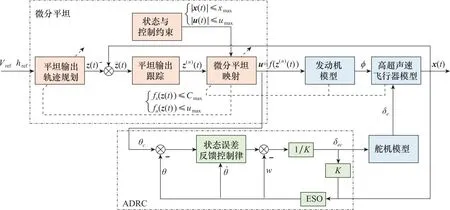
图2 基于微分平坦的控制系统框图Fig.2 Control system diagram based on differential flatness

外环子系统动力学模型为

(16)

特别地,俯仰角θ在外环子系统为中间控制变量。针对高超声速飞行器外环模型,设计控制器完成期望输出状态的跟踪。

下面利用微分平坦理论对动力学方程进行平坦化处理。

选择飞行器状态变量速度V和地心距r作为平坦输出

(17)

根据微分平坦理论,需要通过推导将状态量[V,r,γ,α,q]T和控制量[Φ,δe]T用平坦输出量[z1,z2]T及其导数表达。

首先,可以根据模型中的地心距动力学方程解得

(18)

进一步地,对其求微分可得

(19)

至此已得到全部3个状态量的平坦输出表达,下面求取控制量的平坦输出表达式。

华昌化工植物营养中心农化专员姜在利从示范田和对比田分别选取了一株玉米，现场进行对比实验。华昌玉米样板田底肥施用了锌硼友（27-7-9）免追肥。和普通田块对比非常明显，示范田根冠32cm，茎秆5cm，而普通田根冠25cm，茎秆3cm。华昌示范田根系发达、茎秆粗壮，有效增加了肥料利用率，大大减少了养分流失。现场也可以直接看到华昌示范田玉米叶片更加肥厚，果穗也更加粗壮饱满，有明显的增产增收效果。零售商和种植大户对华昌产品的品质和使用效果给予了很大的肯定。而他们的评价也是华昌众多用户共同的心声。

将式(17)～式(19)代入模型中:

(20)

其中,

(21)

解得攻角的平坦输出表达式:

(22)

其中,

(23)

可得

(24)

为了实现俯仰角速率约束,对式(24)求导,得到

(25)

式中:

(26)

T=mΔ3+Δ4

(27)

式中:

(28)

节流率表达式为

(29)

综合式(17)、式(18)、式(22)、式(29),外环子系统的状态、控制输入和原输出都可以用平坦输出z及其有限阶导数表示为

(30)

式中:x=[V,h,γ]T;u=[θ,φ]T;f(·)=[fx(·)fu(·)]T。

至此,外环非线性系统的状态及控制输入已通过微分平坦理论映射为2个平坦输出动态。因此,只需要规划合理的平坦输出动态,即可得到所需外环控制输入,得到理想的系统动态。

可以在最优控制理论框架下构建飞行器运动轨迹规划模型: 在动力学方程、状态与控制输入物理限制等多种约束条件下,确定一条从初始状态到期望终端状态的转移轨迹,使得指定的性能指标最优,选取最节能即过程控制量最小为性能指标,则其数学描述如问题2所示。

问题 2求解平坦输出z(t)(t∈[t0,tf])可以最小化性能指标:

(31)

同时满足初始终端条件、边界约束、控制饱和约束:

{z(t0)=z0

z(tf)=zf

(32)

|fu(z(t))|≤umax

(33)

|fx(z(t))|≤Cmax

(34)

由此可见,相较于问题1,问题2 避免了微分方程的约束,同时降低了规划空间维数,使得转换所得的问题更易求解,计算效率更高。

利用参数化平坦输出的映射Chebyshev伪谱法[27]将平坦输出规划问题转化为非线性规划问题求解。确定平坦输出在映射CGL(Chebyshev-Gauss-Lobatto)点处取值z(λk)(k=0,1,…,N)以及期望终端时刻tf,使得性能指标满足,同时满足初始终端条件、边界约束、控制饱和约束:

(35)

-umax≤fu(z(λk))≤umax

(36)

fx(z(λk))≤Cmax

(37)

得到最优平坦输出序列zr(λk)(k=0,1,…,N)后,利用重心Lagrange插值法可以获得平坦输出随时间变化关系zr(t)(t∈[t0,tf])。

求解规划期望平坦输出后,构建线性系统

(38)

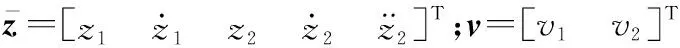
构建反馈跟踪控制律:

(39)

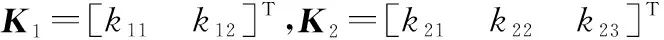
3 基于ADRC的姿态跟踪控制

针对内环子系统,结合系统气动表达式可得内环纵向姿控动力学方程:

(40)

定义如下扩张状态等系统定义:

(41)

系统可以写为

(42)

构建ESO:

(43)

式中:L=[l1,l2]T为ESO增益参数。

观测器可以实现系统的状态估计,特别地,观测器状态z2可以跟踪扩张状态x2。为了进一步减少控制参数,降低控制参数整定难度,观测器增益系数定义为

(44)

式中:ω0为观测器带宽。至此观测器中只有唯一待设计参数ω0,这极大地降低了参数整定的复杂度,为控制系统设计提供了方便。

设计控制输入:

(45)

式中:z2为x2的估计值。若观测器达到稳态,实现了状态估计,那么可以得到原姿控系统动态为

(46)

这里将伪控制量u0设计为PD形式:

(47)

式中:θc为期望俯仰角。

结合式(45)和式(47),得到线性ADRC控制律为

(48)

文献[28]给出了线性ADRC稳定性和鲁棒性的频域分析。控制器分为两大组成部分:一是利用ESO估计系统总扰动,不依赖于精确的模型信息,使得系统鲁棒性得到提高;二是利用补偿后的PD反馈控制律完成跟踪控制,既继承了传统PID控制直观、稳定、有效的优势,又在此基础上极大地优化了控制系统性能。

微分平坦和ADRC结合的综合控制方法确保了外环的控制精度,利用了微分平坦的特性指导了轨迹规划,优化外环控制性能。与此同时内环结合ADRC方法避免了整个系统利用微分平坦推导的微分爆炸,以及严重的模型依赖问题。利用了ADRC的强鲁棒性,并避免了串级ESO的出现,改善系统性能。

4 仿真分析

为了验证所提出控制方法的有效性,采用第3节所设计的控制器,以高超声速飞行器模型作为控制对象,进行闭环仿真。

首先设置模型参数及初始条件如表1所示。

表1 模型参数及初始条件Table 1 Model parameters and initial conditions

通过微分平坦理论对模型平坦线性化处理,并采用映射Chebyshev伪谱法参数化平坦输出,对最终转换所得非线性规划问题,调用fmincon函数进行求解,其参数TolFun、TolX和TolCon均设置为10-6。

依据性能指标规划所得飞行器参考过程轨迹如图3所示。

图3 平坦输出参考轨迹Fig.3 Reference trajectories of flat outputs

其中,红色圆圈代表映射CGL点处平坦输出的取值,其余位置为映射点经过重心Lagrange插值获得。

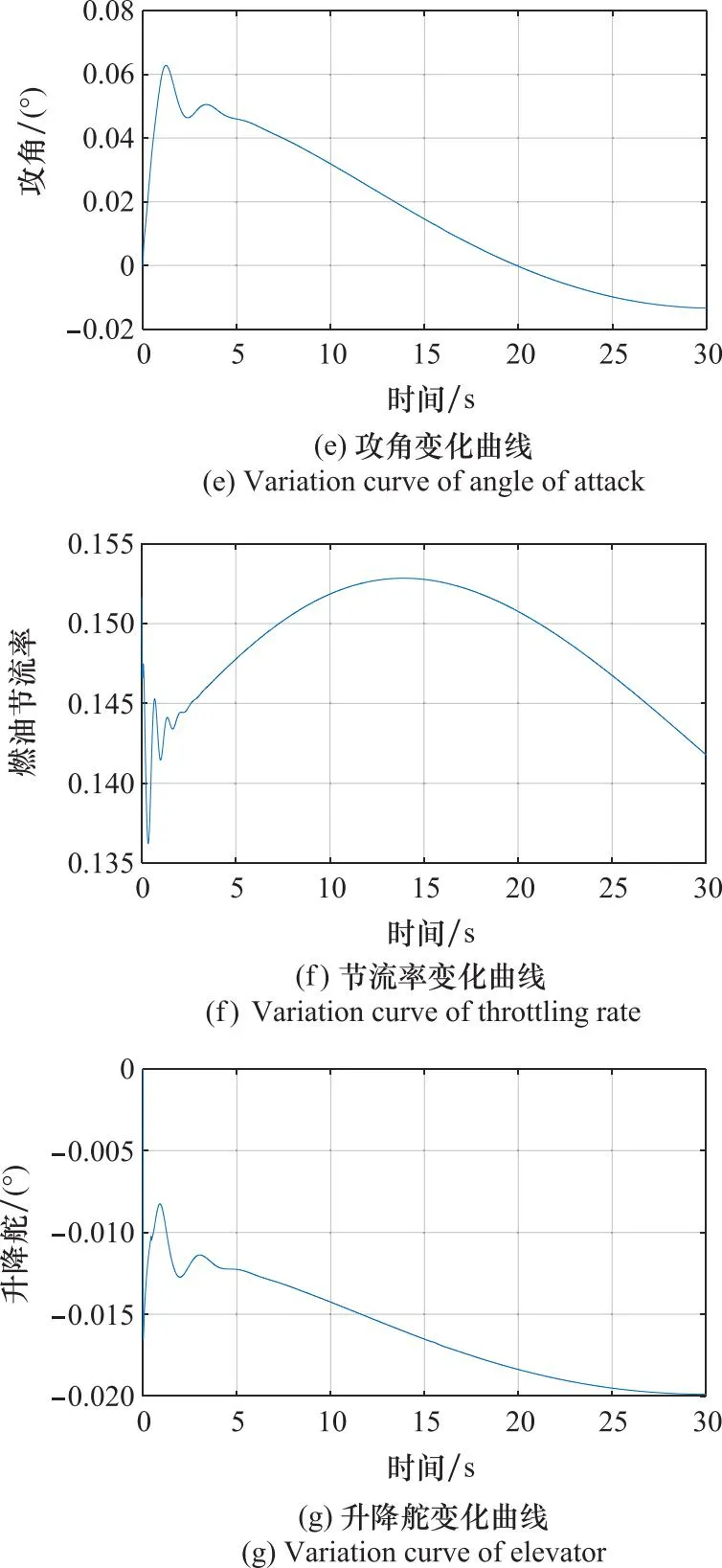
图4 轨迹跟踪仿真结果Fig.4 Simulation results of trajectory tracking

由图4所示仿真结果可以看出,速度和高度跟踪效果良好,经过30 s的时间完成动态过程,达到期望的终端速度和高度。误差存在的原因主要为两方面:一方面为期望平坦输出的高阶导数误差不可避免,若期望轨迹为解析可微分形式,则代入控制器后可有效减小误差。另一方面为系统参数不确定性和控制器自身性能影响。在Chebyshev 伪谱法优化平坦输出下,整个过程中控制输入和过程状态全程在约束范围内,变化较为平缓,控制输入较小。

为了验证所提出方法的鲁棒性与优势,对其所有气动和环境参数做±20%的随机平均概率摄动处理,以验证其在不确定条件下的控制性能。以文献[29-30]中的全微分平坦跟踪控制作为参考对比方法1,以文献[16]中的串级ADRC设计方法作为参考对比方法2。对比仿真结果如图5所示。

图5 蒙特卡罗仿真结果Fig.5 Results of Monte-Carlo simulation

仿真结果表明,所提出基于微分平坦的ADRC跟踪控制方法性能良好,且实现了模型具有不确定性时的轨迹跟踪,高度通道跟踪精度和控制平稳度都具有一定的优势,在参数摄动条件下控制器具有较好的鲁棒性。

5 结 论

本文研究了考虑约束条件的高超声速飞行器的纵向轨迹跟踪问题,提出一种结合微分平坦的ADRC跟踪控制方法,实现了带有状态及控制输入约束下高超声速飞行器的稳定轨迹跟踪。该方法的优势主要在于两方面:一是微分平坦在线性化模型的同时实现了过程状态和控制输入向平坦输出的映射,将高阶模型微分动态的多约束问题转化为了平坦输出的轨迹优化问题,降低了计算维数、提高了计算效率;另一方面是基于ADRC的姿态控制系统极大地增强了系统的鲁棒性,其与微分平坦的结合应用在阶数较高的轨迹跟踪问题中既无需使用高阶或串级ESO而损失性能,又能减小方法的模型依赖问题,使得整个系统跟踪控制性能更好,鲁棒性更强。仿真结果显示,基于微分平坦的优化轨迹满足了要求的过程约束,轨迹跟踪效果良好,鲁棒性较强。