基于SINS/OD失准角观测的垂线偏差测量方法

李新宇, 周召发,*, 张志利, 郝诗文, 梁 哲

(1. 火箭军工程大学导弹工程学院, 陕西 西安 710025;2. 火箭军工程大学兵器发射理论和技术国家重点学科实验室, 陕西 西安 710025)

0 引 言

垂线偏差是由于地球形状不规则、质量分布不均匀引起的正常重力与真实重力在方向上的角度偏差,是机动武器系统建立射前初始基准的重要信息[1-3]。传统的垂线偏差测量方法是基于数字天顶仪观测恒星的天文大地测量法,可以在固定点获取高精度的垂线偏差信息[4-5]。但由于操作复杂、时间较长、场地局限的缺点限制了其测量效率和范围,基于这种重力信息外部保障的作战模式严重限制了武器系统的生存能力和快速反应能力。

捷联惯性导航系统/里程计(strapdown inertial navigation system/odometer, SINS/OD)组合导航依赖于惯性器件和里程计,具有全天候、隐蔽性强、自主无源等优点,成为车辆必不可少的导航方式[6-8]。组合导航姿态失准角与垂线偏差之间存在复杂的耦合关系是影响垂线偏差测量精度的主要因素[9],突破该技术壁垒成为近年来的研究热点问题。文献[10]从理论上分析了单轴旋转惯性导航系统/全球定位系统(inertial navigation system/global positioning system,INS/GPS)组合导航模式下垂线偏差与系统姿态精度的相互影响,但没有给出具体的解决办法。文献[11]通过星敏感器和激光陀螺组合体(laser gyroscope unit,LGU)建立高精度姿态基准的方法获取姿态失准角误差,实现垂线偏差与姿态误差的解耦,但该方法无法完全消除LGU中的初始姿态误差。文献[12]对LGU姿态误差精确建模,通过Kalman滤波的方式实现与垂线偏差的分离,但该方案的成本和复杂度依旧较高,且无法保证单点的测量精度。文献[13]利用零速修正改善INS姿态误差的角度提升了垂线偏差测量精度,但该方法必须定时停车,限制了测量载体的机动性能。文献[14]根据垂线偏差的波长信息区分建模方法,进一步提高了测量精度,但使用全球导航卫星系统(global navigation satellite system,GNSS)信息后自主性又是一大挑战。文献[15]推导了对准失准角与垂线偏差的关系,在此基础上提出垂线偏差相对测量法,但该方法需要进行两次高精度对准,操作复杂且难度较大。

本文提出一种新的垂线偏差测量方法。由出发点精确的垂线偏差获取姿态失准角误差,沿机动路径获取组合导航的姿态失准角,通过迭代递推将垂线偏差与姿态失准角解耦,进而求解垂线偏差。通过仿真验证该测量方法的可行性,并分析了该方法测量精度与机动路径长度的关系。最后通过跑车实验对实际测量效果进行验证。

1 垂线偏差与失准角的耦合关系

本文选取东北天坐标系为导航坐标系n,为了便于分析,只考虑惯性器件的零偏误差,并假定载体处于稳定的匀速运动状态,即满足:

(1)

1.1 垂线偏差与姿态失准角的对应关系

在导航系下载体速度误差微分方程[16]为

(2)

重力计算误差Δgn由两部分组成,一是由位置误差引入的正常重力模型误差,二是计算重力与实际重力之间的差值[17]。SINS/OD组合导航定位误差在100 m/100 km左右,根据正常重力计算公式[16],第一部分的误差值不足0.03 mGal,故予以忽略。则重力计算误差Δgn可表示为

(3)

(4)

此时式(2)可化简为

(5)

(6)

(7)

式中:η、ξ分别表示垂线偏差卯酉分量和子午分量。由式(6)和式(7)得垂线偏差与姿态失准角的关系:

(8)

(9)

1.2 垂线偏差与姿态失准角误差的关系

由式(6)和式(7)可知,yE、yN为n系下东向和北向的可观测项,则失准角的观测值可表示为

(10)

(11)

(12)

(13)

式(12)和式(13)表示垂线偏差与失准角误差的关系。

1.3 姿态失准角与垂线偏差测量误差的关系

直接差分法动基座重力测量的原理表达式在n系下[18]可以表示为

(14)

式中:δgn表示重力扰动矢量,其他各项的物理含义同上文。对式(14)进行变分后即可得到动基座重力测量的误差模型[19]为

(15)

(16)

式(16)结合式(1)进行化简并在n系下展开东向、北向的分量形式为

(17)

(18)

结合垂线偏差的定义可得姿态失准角对垂线偏差测量误差的影响关系式为

(19)

(20)

由上述推导结果式(8)、式(9)、式(12)、式(13)、式(19)、式(20)可知,垂线偏差与姿态失准角之间存在对应关系,但两者之间又相互影响,存在复杂的耦合关系。此外,组合导航姿态失准角通过Kalman滤波逐渐会收敛,无法直接用于反馈变化的垂线偏差信息。

2 垂线偏差测量方法

针对上述存在的耦合关系及直接使用姿态失准角求解垂线偏差的弊端,本文提出一种从基准点出发,沿机动路径迭代递推的分步计算方法,将可以反映垂线偏差变化的姿态失准角误差引入导航系统失准角的观测,进而实现垂线偏差的动态测量及停车单点测量。

2.1 初始基准信息的获取

本文所提测量方法需要在初始垂线偏差信息已知的前提下进行,天文大地测量法可以静态获取基准点高精度的垂线偏差[21-23]。在地球表面P点安置数字天顶仪和经纬仪,分别测定P点的天文坐标为(φ,λ)和大地坐标(B,L),根据天文大地测量法可得P点的垂线偏差为

ξ=φ-B

(21)

η=(λ-L)cosφ

(22)

2.2 垂线偏差测量

姿态失准角和加速度计零偏可以通过SINS/OD组合导航系统的状态量中实时估计出。组合导航过程选取15维状态量的Kalman滤波,详见参考文献[24]。本文提出的基于姿态失准角误差观测的垂线偏差测量方法按以下步骤进行。

步骤 1基准信息获取。载体在初始基准点处静止5 min完成初始对准,其中包含1 min粗对准和4 min的双位置精对准。双位置对准提高了惯性器件的可观测性,通过精对准过程中的Kalman滤波可以有效估计出加速度计零偏误差,并通过天文大地测量法获取精确的η0、ξ0,而后代入式(12)和式(13)中计算该点的失准角估计误差值δφ0。

步骤 4计算垂线偏差。由于垂线偏差引起的失准角误差在步骤3中得到校正,将步骤3得到的失准角和对应时刻组合导航给出的可观测项y代入式(8)和式(9),即可计算该位置的垂线偏差。

步骤 5路径递推垂线偏差测量。将步骤4得到的垂线偏差代入步骤1作为下一时刻的基准信息,导航系统实时更新状态量和可观测项,沿路径迭代递推逐步将姿态失准角与垂线偏差的相互影响分离,实现垂线偏差的高精度测量。

垂线偏差测量流程图如图1所示。

图1 垂线偏差测量流程图Fig.1 Flow chart of the deviation of vertical measurement

3 仿真与实验

SINS/OD组合导航高度通道是独立的[25],本文不考虑高度变化对垂线偏差的影响。组合导航系统水平方向上的定位误差在100 m/100 km左右,由此引入的垂线偏差小于0.01″,故行驶路径在100 km以内时该项误差可以忽略[26]。

3.1 仿真条件

初始基准点设定为(N34°, E110°,500 m),初始垂线偏差真值由EGM2008模型计算得到。为尽量满足实验条件和实际跑车情况,载体存在若干次转弯但保持匀速的运动状态,行车轨迹与载体运动参数如图2和图3所示。上述为轨迹理论值,轨迹真值由SINS/OD组合导航给出,其仿真参数如表1所示。

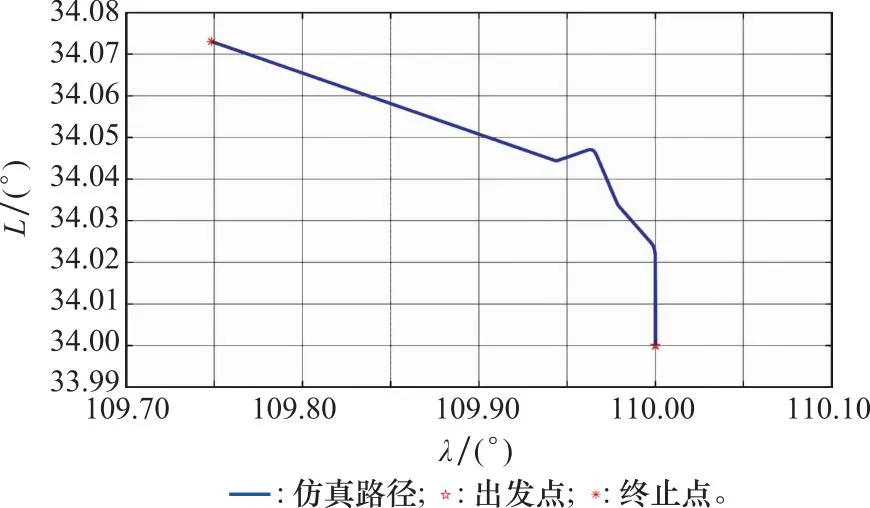
图2 仿真轨迹Fig.2 Simulation track

图3 仿真轨迹参数Fig.3 Trajectory parameters of simulation

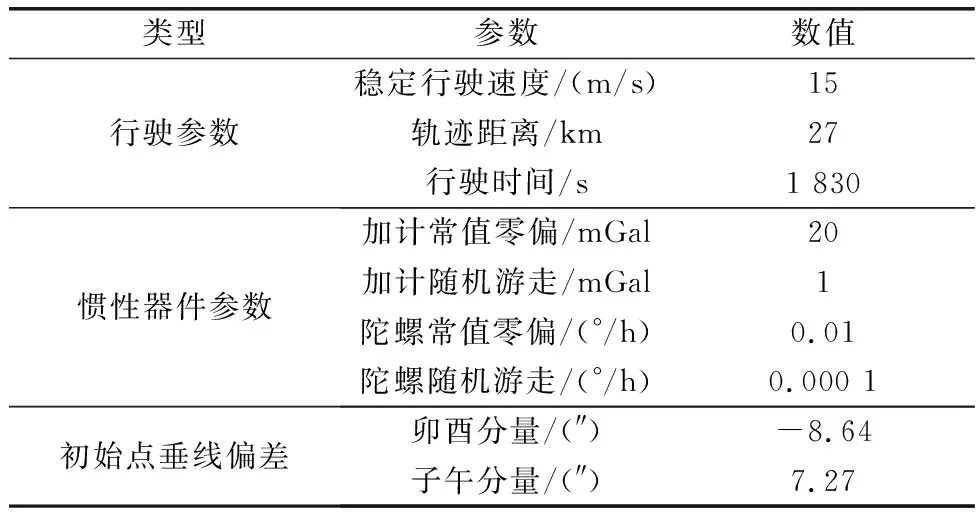
表1 仿真参数Table 1 Simulation parameters

3.2 仿真结果与分析

EGM2008沿组合导航设定的仿真轨迹计算所得的垂线偏差作为仿真实验的真值,按照图1测量流程得到垂线偏差的测量值。将直接使用对应关系求解而不进行迭代递推解耦的测量结果作为对比组,测量结果如图4所示。通过式(19)和式(20)计算垂线偏差的理论测量误差,仿真实验测量误差和理论计算结果如图5所示,统计测量结果精度如表2所示。

图4 里程27 km时测量结果及真值Fig.4 Measurement result and true value at a mileage of 27 km

图5 行驶里程27 km时垂线偏差测量误差Fig.5 Error of the deviation of vertical measurement at a mileage of 27 km

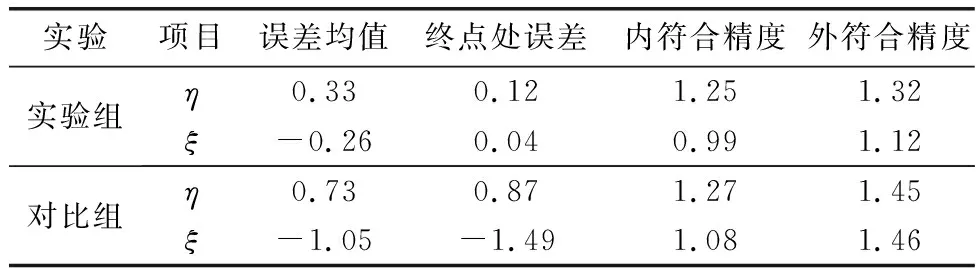
表2 里程为27 km时的仿真测量精度Table 2 Measurement accuracy of simulation at a mileage of 27 km (″)

由图5可知,对比组测量误差与理论计算值变化趋势一致,验证了失准角与垂线偏差的耦合关系。从表2可知,在仿真行驶27 km时,实验组的各项精度均优于对比组,且实验组的误差均值在0.35″以内,得到了较高精度的垂线偏差,验证了该方法的有效性和可行性。为充分验证测量方法的环境适应性和可靠性,将仿真路径设置为177 km,沿途的垂线偏差有明显变化,再次进行仿真实验。测量结果及误差如图6和图7所示,测量结果精度统计如表3所示。

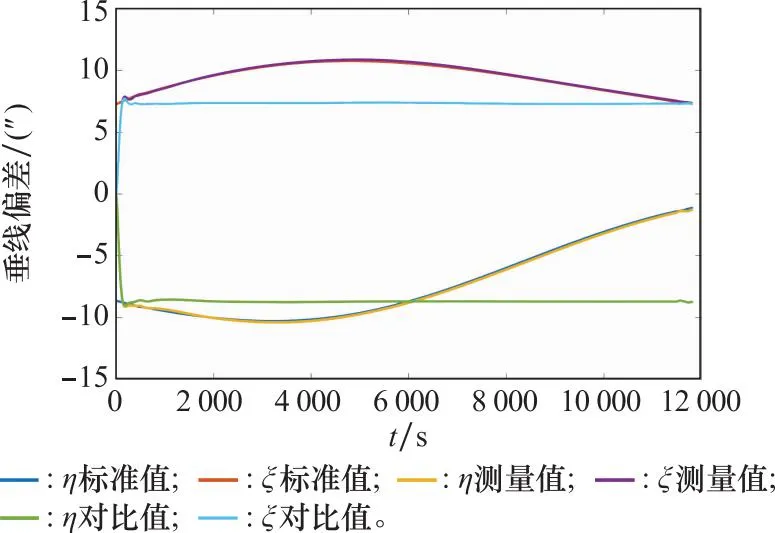
图6 行驶里程177 km时测量结果及真值Fig.6 Measurement result and true value at a mileage of 177 km

图7 行驶里程177 km时垂线偏差测量误差Fig.7 Error of the deviation of vertical measurement at a mileage of 177 km

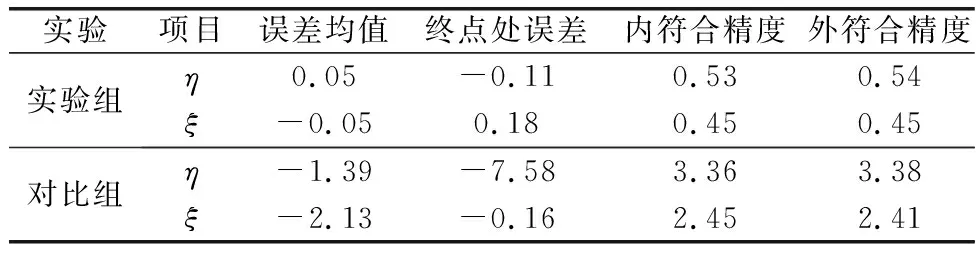
表3 里程为177 km时的仿真测量精度Table 3 Measurement accuracy of simulation at a mileage of 177 km (″)

由测量结果可以看出,实验组测量结果同真值一起波动,而对比组无法获得变化的垂线偏差信息,测量误差也明显大于实验组。

文献[26]给出了定位误差引入重力扰动测量误差的计算方法,指出300 m的定位误差造成的重力扰动误差不会超过0.2 mGal,对应垂线偏差大约为0.04″,故当路径足够长时,该误差不可忽略。为了研究测量精度与路径长度的关系,改变仿真路径长度进行多次仿真实验。得到误差均值与仿真路径长度关系如图8所示。由图8可以看出,在短距离内测量精度随路径长度的增加逐渐提升,这是由于随着组合导航过程的进行,姿态失准角逐渐收敛,加速度计零偏估计趋于真值,引起当前时刻的垂线偏差精度提高,故下一时刻失准角误差的精度也随之提升,从而迭代递推形成一个正反馈的过程,测量精度逐步提升。但并非路径越长测量精度越高,因为长距离的SINS/OD组合导航定位误差较大时,引入的垂线偏差误差不再是小量[27],将会直接影响测量效果,故测量精度随着路径长度过大地提升而下降。

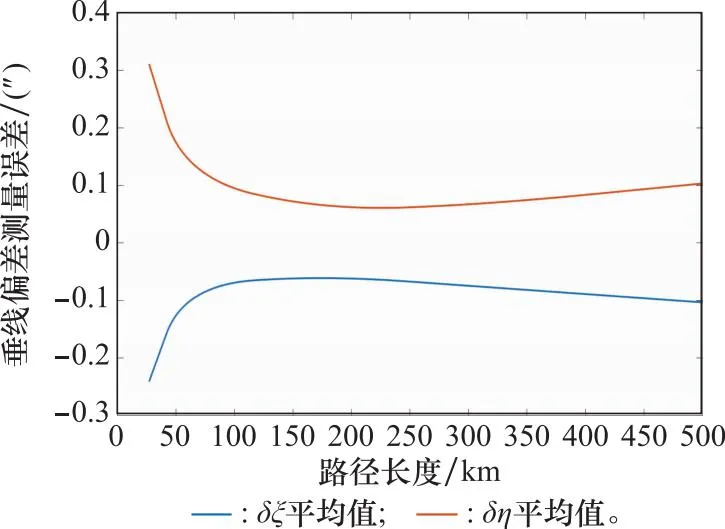
图8 误差均值随路径长度变化关系Fig.8 Correlation of error mean with path length

仿真结果表明最佳的测线路径长度大约为200 km,此时可以很好地避免定位误差的影响。若必须进行长距离跑车实验,可以辅助GPS用于位置修正,也可以选择在有基准地标的道路上进行实验,在地标处停车对位置信息重新装订。本文所提的测量方法可以满足每200 km停车校正一次,并不会对测量效率造成太大影响。

3.3 实验结果与分析

本文通过跑车实验来检验实际测量效果,行车时间总计55 min,总里程35.89 km。如图9所示,该实验车配备有高精度捷联惯导、轮式里程计、气压高度计和GPS接收机。GPS的定位精度为1 m,故以此作为定位基准,气压高度计用于控制高度通道的发散[28-29]。基于上述条件选用15维状态量的Kalman滤波信息融合进行SINS/OD组合导航解算,定位结果及误差如图10和图11所示。

图9 实验用车Fig.9 Test vehicle

图10 组合导航定位结果Fig.10 Positioning result of integrated navigation

图11 组合导航定位误差Fig.11 Positioning errors of integrated navigation

姿态失准角观测值及加速度计零偏通过组合导航解算中的Kalman滤波获得最优估计,并用于第2节中所述迭代递推分步计算实现垂线偏差的测量,两者的估计结果如图12和图13所示。

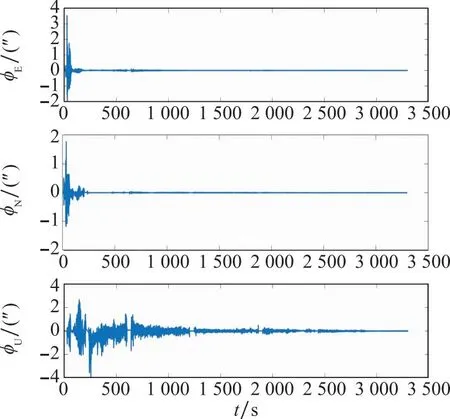
图12 姿态失准角估计值Fig.12 Estimation value of attitude misalignment angle

图13 加速度计零偏估计结果Fig.13 Zero offset estimation results of accelerometer

初始基准点的垂线偏差值通过数字天顶测量仪事先获取,而后驶往下一个基准点,在终点处进行精度的比对。沿测线的EGM2008模型计算值及初始点和终点实测值经过平差后作为测线垂线偏差真值[30]。理论真值及测量结果如图14所示,测量结果在真值附近波动,作差后得到垂线偏差测量误差图如图15所示,在终点处可以得到相对稳定的测量结果,统计跑车实验测量精度如表4所示。

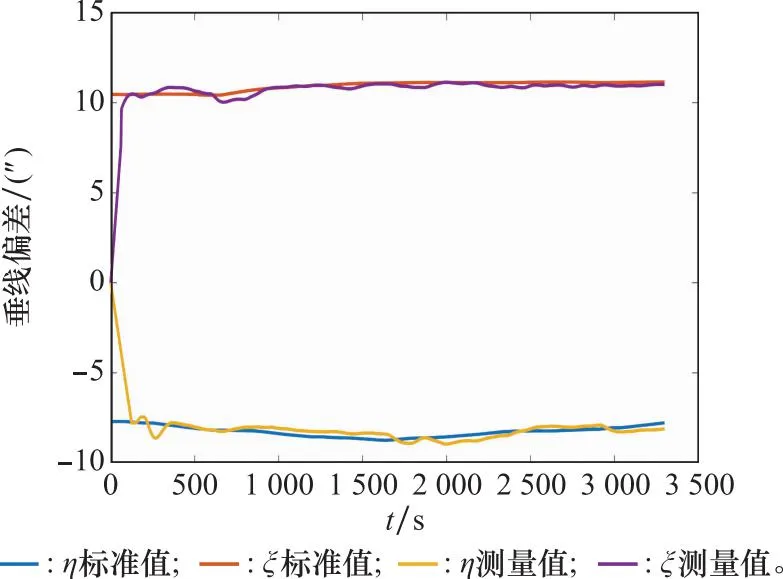
图14 测量结果及理论真值Fig.14 Measurement result and theoretical true value

图15 垂线偏差测量误差Fig.15 Deviation of vertical measurement error

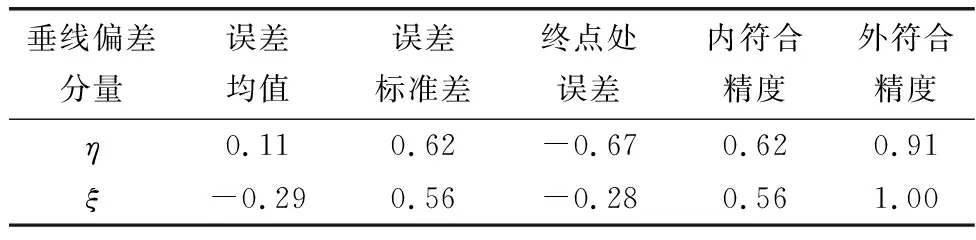
表4 实验测量精度统计Table 4 Statistics of measurement accuracy of experiment (″)

图16所示为沿测线垂线偏差测量结果内外符合精度统计直方图,横坐标为精度范围,纵坐标为不同精度所占测量结果的个数。结合表4和图16可知,跑车路径上垂线偏差误差均值在0.3″以内,终点处误差在0.7″以内,且绝大部分测量结果的符合精度分布在-1″～1″,可见该方法在整个跑车过程中测量精度均保持在较高水准,可以实现垂线偏差的动态测量。

图16 内外符合精度统计直方图Fig.16 Histogram of inner and outer coincidence accuracy

4 结 论

本文在SINS/OD组合导航姿态失准角观测的基础上提出一种迭代递推分步计算的垂线偏差测量方法。仿真结果表明,沿测线的动态测量以及终点处的单点测量均可达到较高的测量水平,且测量精度与递推路径长度有关。跑车实验验证该方法的实用性,结果表明该方法的误差均值可达0.3″。垂线偏差动态测量可提高重力信息的测量效率,对丰富地球重力场具有重要价值;单点垂线偏差的高精度快速获取,为机动武器系统建立射前基准信息提供条件,推动导弹武器系统无依托机动发射和全域作战快速发展。