基于鲁棒观测器的深度强化学习垂直起降运载器姿态稳定研究
2024-03-05李彦铃罗飞舟葛致磊
李彦铃, 罗飞舟, 葛致磊,*
(1. 西北工业大学航天学院, 陕西 西安 710072; 2. 中国运载火箭技术研究院, 北京 100076)
0 引 言
随着人类对太空的不断探索,对运载火箭技术的要求也逐步提高,迄今为止国内运载火箭型号几乎只能单次使用,而垂直起降技术的发展为运载火箭重复使用开辟了一条新道路[1-2]。垂直起降运载器从提出伊始就受到各国航天机构及科研人员的高度重视,随之多种垂直起降运载器应运而生,如ROOST/ROBOS[3]、Apollo Lunar Module[4]、DC-X/DC-XA[5]、RVT[6]、Falcon系列[7]等。
垂直起降运载器控制系统的设计是其飞行控制技术的核心,而姿态稳定是运载器平稳飞行的前提。根据当前的研究和工程实践,稳定飞行器姿态控制是一个复杂而关键的问题,需要选择合适的控制策略以实现期望的控制效果[8-9]。滑模控制、模型预测控制和鲁棒控制等算法被广泛应用于该领域,但存在对模型准确性和全面性的依赖问题[10-12]。一方面,如果模型表达不够准确或参数无法精确表达,则这些控制方法可能无法获得理想的效果;另一方面,过于复杂的模型也会增加控制器设计难度。因此,应在模型准确性和复杂度之间进行权衡并寻找最优解。虽然比例-积分-微分(proportional-integral-derivative, PID)控制仍是目前工程上主流控制算法之一,但其抗干扰能力和处理模型不确定性的能力相对较弱[13]。近年来,许多改进PID控制方法被提出,其中自适应模糊PID控制结合模糊控制和PID控制的优点,被广泛应用于垂直起降无人机姿态控制[14-16]。
同时,长细比的增加降低了运载火箭弯曲模态的固有频率,低阶弹性振动容易与火箭本身的振动耦合,使控制更加困难,对于高阶弹性振动可以设计陷波滤波器进行抑制,但是对于低模态的弹性振动,特别是振动频率接近箭体的固有频率时,弹性振动的抑制比较困难,因此目前低阶弹性振动干扰下的箭体姿态稳定问题仍然是航空航天领域的难题[17]。
随着信息技术的进一步发展,人工智能技术的飞速发展也切实影响到了传统控制领域。基于机器学习的智能飞行控制策略成为研究焦点[18]。即使对于不确定的非线性模型,智能控制算法也能实现良好的控制效果,这主要得益于深度神经网络强大的非线性拟合能力[19]。但是通过神经网络的实现行为克隆的方法有时效果会很差,这是由于网络收集的数据和正确数据不匹配[20]。因此,为了克服监督学习方法的不足,研究人员提出了深度强化学习方法。在2005年,Waslander等人首次将强化学习算法应用在四旋翼模型飞行控制问题[21]。近些年来,深度强化学习已经被应用于无人机控制[22]、机器人控制[23]、自动驾驶[24]以及制导一体化[25]等领域,都取得了出色的效果。然而,上述研究都仅仅停留在仿真环境中,在真实环境和仿真环境之间存在着许多差异,将从仿真环境中学习到的飞机模型直接应用到实际的环境中会导致许多问题,如精度和稳定性下降,这才是研究的难点[26]。
本文主要研究运载器验证机在垂直起降阶段的俯仰通道的姿态稳定问题,该验证机俯仰通道开环系统的截止频率ωc=1.8 Hz,根据带宽与截止频率的关系可得系统带宽ωb=1.6ωc=2.88 Hz,若是一阶振动频率和系统带宽相差10倍以上,则完全没有必要考虑一阶振动的影响,使用频率隔离法就能设计出满意的控制器。然而,当振动频率模态频率略大于系统带宽时,弹性振动很难与工作频率分隔开,此时频率隔离法不适用,需要研究其他策略[27-28]。经过辨识,本文的研究对象一阶振动模态频率为20.25 rad/s,二阶振动模态频率为180.88 rad/s,因此对一阶振动模态抑制难以使用频率隔离法。本文中,首先为了避免欧拉角奇异,以垂向地理坐标系作为惯性坐标系,建立动力学和运动学模型。其次,考虑垂直起降过程中的弹性振动、模型不确定性等干扰因素,设计基于鲁棒观测器的深度强化学习控制策略。设计鲁棒观测器对姿态变量与复杂的弹性振动进行重构,使得弹性振动变量转换为易于控制的具有箭体姿态特征的附加姿态,并将带有附加姿态的重构箭体姿态作为深度强化学习神经网络的输入,输出最优控制力矩指令,以稳定垂直起降运载器验证机在垂直起降过程中俯仰姿态角和弹性振动。本文从仿真和实物上验证了面对包含弹性振动模型不确定性的复杂受控系统,相较于工程中应用广泛的自适应模糊PID控制,本文设计的控制算法能够更好地稳定火箭姿态。
1 模型建立
本文以实验室一台自制的运载火箭验证机作为研究对象,该验证机是大型运载火箭的合理微型化,如图1(a)所示,同时为了模拟真实运载火箭在飞行过程中出现的弹性振动干扰,在验证机上搭载了弹性舱段,细节如图1(b)所示。

图1 垂直起降运载器验证机Fig.1 Vertical takeoff and landing vehicle validation machine
由于运载器在垂直起降飞行时姿态角的定义不同于常规飞行器,为了避免运载器在垂直起降过程中出现的欧拉角奇异问题,本文采用垂向地理坐标系(“天东北”,即UEN)作为火箭的惯性参考坐标系,如图2所示。

图2 垂向地理坐标系Fig.2 Vertical geographic coordinate system

(1)

为便于建立运载器垂直起降动力学模型,本文做出以下假设。
假设 1重力加速度不会随着运载器飞行高度的变化而变化,忽略地球曲率。
假设 2运载器的构型和质量分布关于箭体纵轴对称,所以惯性积Jxy=Jyz=Jxz=0[29]。
在上述假设成立的前提下,机体坐标系下绕运载器质心转动的动力学方程如下所示:
(2)
式中:M=[Mx,My,MZ]T为运载器受到的合力矩,且M=Mc+Md,Mc=[Mcx,Mcy,Mcz]T是控制力矩,Md=[Mdx,Mdy,Mdz]T是总的干扰力矩,包括重力力矩、气动力矩等干扰力矩。
本文研究俯仰通道的控制器的设计,弹性振动方程如下所示:
(3)
联立式(1)~式(3),同时考虑到垂直起降飞行模式下的滚转角非常小,俯仰角速度是影响θv的主要因素,故可得到运载器俯仰通道的动力学模型如下:
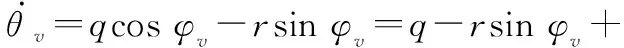
(4)
式中:qi为第i阶弹性振动位移;ξi为第i阶弹性振动的阻尼比;ωi为第i阶弹性振动的振动频率;D1i为第i阶弹性振动和俯仰角的耦合系数;D2i为第i阶弹性振动与控制力矩的耦合系数;Qiy是第i阶弹性振动受到的广义干扰力矩。dθv1可以看作俯仰通道的干扰量。
对式(4)两边求导可得
(5)
将式(2)中的第2式代入式(5)为
(6)
式中:m表示箭体弹性振动的阶数。
式(6)进一步写为
(7)
式中:
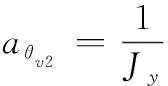
2 垂直起降姿态控制器设计
垂直起降运载器俯仰通道姿态控制器的设计分为两个部分:第一部分是鲁棒观测器的设计,设计鲁棒观测器使得垂直起降过程中的低阶弹性振动成为刚体姿态的附加姿态角,实现弹性振动的被动抑制;第二部分设计深度强化学习控制器,将鲁棒观测器输出的带有附加姿态的姿态角和姿态角速度作为输入从而决策出控制指令,作用给环境。环境反馈给近端策略优化(proximal policy optimization, PPO)智能体下一时刻的状态、奖励信息以及结束信号,PPO智能体以最大化累计奖励为目标,不断优化深度神经网络参数,实现运载器姿态稳定[30]。这里需要说明的是,此处的附加姿态角和附加姿态角速度是中间量,是鲁棒观测器重构受弹性振动干扰的姿态角和姿态角速度过程中得到的;而带有附加姿态的俯仰角和俯仰角速度是鲁棒观测器的输出量,即为重构后的姿态角和姿态角速度。
2.1 鲁棒观测器设计
首先设计鲁棒观测器,将运载器垂直起降过程中的干扰通过鲁棒观测器转换为箭体姿态的附加姿态角和附加姿态角速度,此时鲁棒观测器的输出是带有附加姿态的俯仰角和俯仰角速度,即重构后的姿态角和姿态角速度,这样可以使干扰对火箭姿态控制的影响大大减小。
考虑箭体控制中纵向通道姿态控制系统具有如下形式:
(8)
引入一个非奇异的变换T,使得
使用SPSS17.0软件处理数据资料,计数数据对比采用x2检验,计量数据对比采用t检验,P<0.05有统计学意义。
(9)
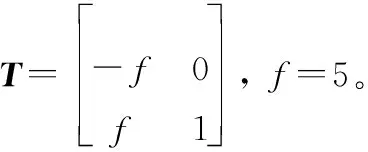
则方程可转化成
(10)
式中:z是变换后的状态向量,由z1和输出信号y构成,z1=-fθv。
根据参考文献[17],针对变换后的动态方程设计观测器如下:
(11)
(12)
(13)

可以得到误差方程:
(14)
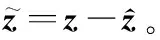
定理 1[32]当k1,k2,…,kn被正确选择时,误差运动是有限时间稳定收敛的。
当系统存在不确定性,即存在参数摄动和外干扰时,特别是当外干扰较大或变化较剧烈时,上述设计的变结构观测控制量v存在较大的抖振,引入边界层进行连续化,即:
式中:p1∈Rp×p是李亚普诺夫方程ATp1+p1A=-Q1的解,Q1是一个对称正定的矩阵;η的取值要满足误差方程李亚普诺夫稳定性条件,Δ是边界层。
2.2 深度强化学习控制器设计

(15)
式中:R(τ)表示每一个回合的累计奖励;pθ(τ)为每一个回合发生的概率,θ是策略π的网络参数,pθ(τ)为一个行动状态序列τ的概率,可以进一步表示为
pθ(τ)=p(s1)pθ(a1|s1)p(s2|s1,a1)pθ(a2|s2)…
(16)
强化学习的目标函数就是最大化累计奖励,即式(15)。
目标函数对网络参数θ求偏导可得
(17)
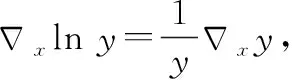
(18)
深度强化学习是将深度学习和强化学习相结合,使算法同时具有深度学习强大的表述能力和强化学习卓越的自适应能力。PPO算法基本已经成为一种最流行的深度强化学习算法,在Open AI开源算法中,也将PPO作为基线算法。其采用Actor-Critic网络结构,其中Actor网络输出动作,Critic网络输出状态价值函数V(st)。
为了得到状态的精确价值估计,PPO算法采用广义优势估计优化价值函数,如下所示:
(19)
式中:δt为时序差分,具体表达式为式(19)第2式;γ和λ是两个重要的参数,γ决定了价值函数的最大值,λ用来平衡偏差和方差。同时,PPO为了提高训练效果,避免策略梯度算法中采样数据利用率低的缺点,引入了重要性采样,智能体采用旧策略πθold与环境交互获得训练数据存入样本池中更新策略πθ,则PPO算法的奖励微分可以表示为
(20)
则似然函数可以表示为
(21)
但是要求两个策略的分布不能差别太大,因此需要进行一定程度的剪切,最终得到的PPO算法:
(22)
式中:θ是策略π的网络参数;ε是剪切比,与文献[30]保持一致,本文中ε取0.2。
2.3 ROB-PPO控制器设计
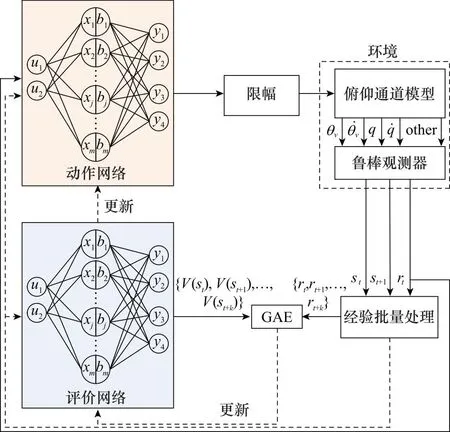
图3 基于鲁棒观测器的深度强化学习运载器垂直起降 姿态控制框图Fig.3 Attitude control block diagram of deep reinforcement learning vehicle vertical takeoff and landing based on robust observer

算法 1 ROB-PPO算法流程伪代码初始化动作网络和评价网络的偏差和权重初始目标网络的偏差和权重For episode=1,2,…,M, do 初始化环境 鲁棒观测器重构姿态,智能体收到初始观测状态s1 For t=1,2,…,T, do 动作网络根据s1选择动作a1,返回给环境 环境对动作a1作出响应,鲁棒观测器重构姿态,智能体受到观测状态s2以及奖励值r1 存储(st,at,rt,st+1)至经验池R 采样Batchsize大小的数据量计算目标函数 更新θold←θ End forEnd for
奖励函数作为指导智能体训练的关键,其好坏决定了智能体能否达到理想的控制效果以及训练速度,对于本文中对垂直起降运载器俯仰通道的控制,在不同的姿态角误差条件下,奖励函数设置为

3 仿真结果及分析
在本节,垂直起降运载器的仿真环境中,应用ROB-PPO的方法训练一个深度强化学习智能体,一旦运载器在仿真环境中成功飞行,将训练好的控制器实现到实物平台上,以测试其在垂直起降运载器姿态控制中的稳定性。
3.1 仿真验证
Actor网络和Critic网络均采用全连接结构,隐藏层激活函数采用 Relu 函数,Actor网络均值激活函数采用tanh函数,方差激活函数为softmax函数。ROB-PPO算法的网络结构和超参数如表1所示。

表1 ROB-PPO算法的网络结构和超参数Table 1 Network structure and hyperparameters of ROB-PPO algorithm

训练强化学习智能体1.2×106回合,得到的训练过程中的平均奖励变化曲线如图4所示。可以看出,经过前2×104回合的探索之后,智能体学会了控制策略,之后的平均奖励值一直收敛,说明智能体已经训练完成。将训练好的网络模型保存,用于控制效果的测试。

图4 ROB-PPO训练平均奖励Fig.4 Average reward for ROB-PPO training
图5和图6中初始姿态角在0 rad到1 rad之间任意取值的条件下,在上述训练好的智能体控制下姿态角和姿态角速度的曲线。根据李雅普诺夫理论,神经网络拟合的动力学系统是渐进收敛的[34]。图5和图6表明即使在初始状态变化情况下,本文训练的控制器均能保证姿态角和姿态角速度收敛到期望姿态,具有稳定性。
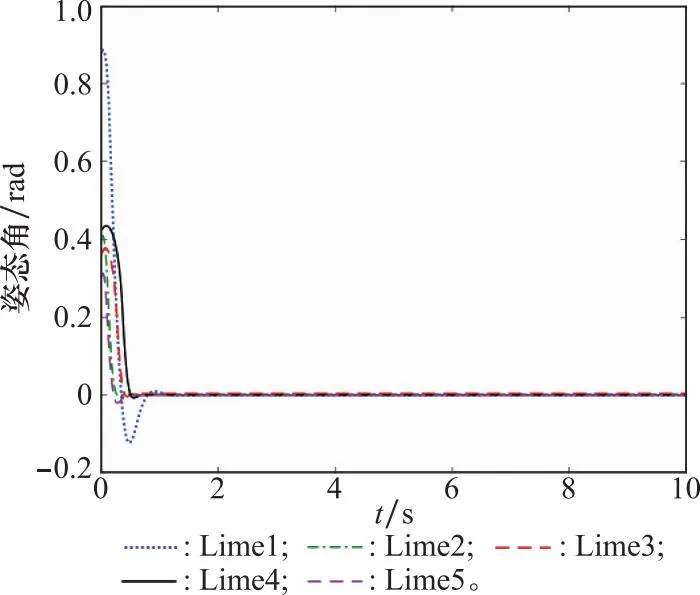
图5 姿态角响应曲线Fig.5 Response curve of attitude angle
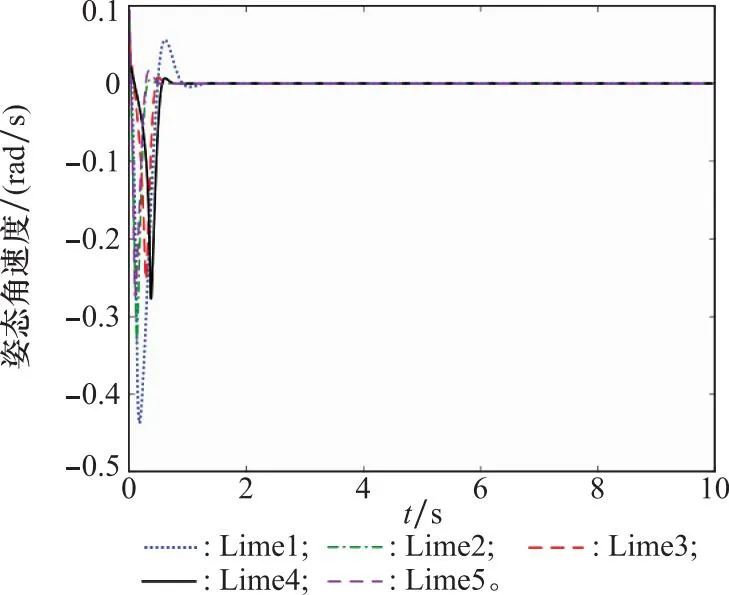
图6 姿态角速度响应曲线Fig.6 Response curve of attitude angle regular
图7~图11给出了本文设计的基于鲁棒观测器的深度强化学习算法和文献[16]提出的自适应模糊PID控制算法的对比图。其中,图7展示了ROB-PPO和自适应模糊PID控制作用下的舵偏角比较曲线,可以看出,与传统自适应模糊PID控制相比,虽然在0.2 s时ROB-PPO的幅值超过了自适应模糊PID,但是在0.8 s就趋于收敛,而传统自适应模糊PID在3 s才稳定,ROB-PPO相较于传统自适应模糊PID控制算法收敛时间加快了2.2 s,可以看出本文设计的控制器在快速性方面表现出色。
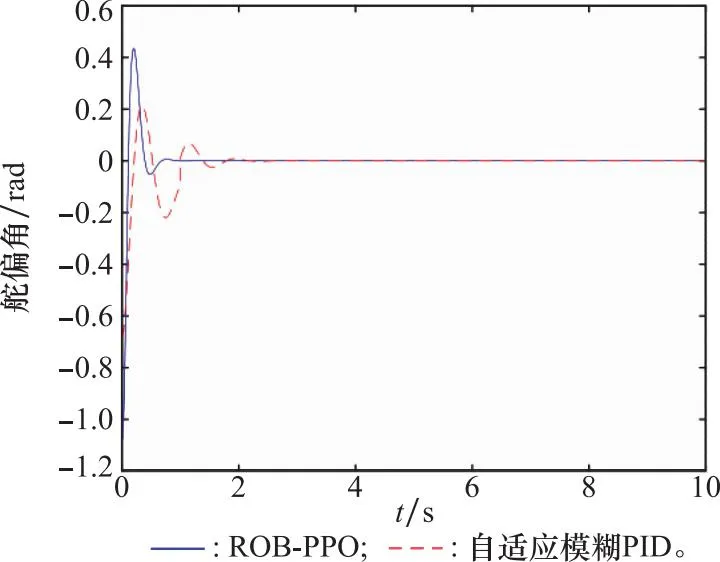
图7 舵偏角比较曲线Fig.7 Comparison curve of rudder deflection angle

图8 俯仰姿态角对比曲线Fig.8 Contrast curve of pitching attitude angle

图9 俯仰角速度比较曲线Fig.9 Pitch angle regular comparison curve
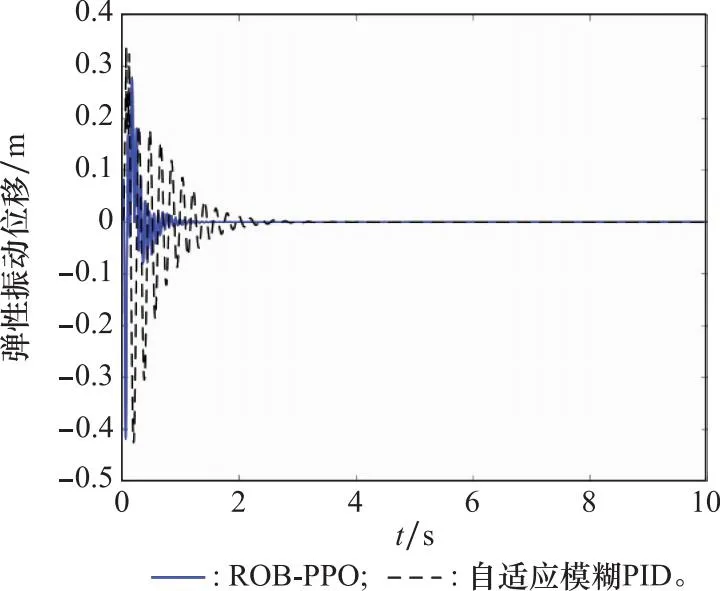
图10 弹性振动位移对比图Fig.10 Comparison of elastic vibration
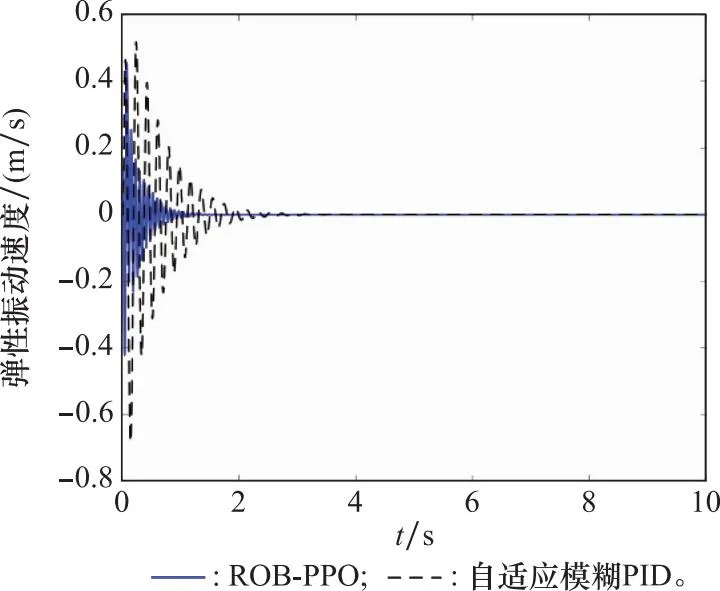
图11 弹性振动速率对比图Fig.11 Comparison of rates of elastic vibration
图8和图9分别展示了ROB-PPO和自适应模糊PID控制作用下俯仰姿态角和角速度的对比曲线。
从图8中可以看出,相较于自适应模糊PID,ROB-PPO算法的控制性能明显提升,俯仰角幅值为0.1 rad,而传统自适应模糊PID控制作用下的幅值达到了0.3 rad;同时,在本文设计的控制器作用下,俯仰角在0.8 s就收敛到平衡位置了。图10和图11分别展示了ROB-PPO和自适应模糊PID控制作用下一阶弹性振动位移和一阶弹性振动速度的对比曲线。
与之前的结论一致,ROB-PPO对弹性振动的抑制效果优于自适应模糊控制,相较于自适应模糊PID控制,弹性振动幅值相差无几,但收敛时间缩短了1.3 s。ROB-PPO控制下的一阶弹性振动位移和速度基本在1 s左右就趋于稳定,而自适应模糊PID控制下在2.3 s才逐渐稳定,体现出ROB-PPO算法具有更好的弹性振动抑制效果。
3.2 实验验证
为了验证所训练的模型在实物运载器姿态控制上的有效性,将训练稳定的智能体搭载在实物平台上,自制运载器从上而下主要分为油料舱、弹性舱、飞控舱以及发动机舱,油料舱主要为运载器提供燃料,弹性舱模拟弹性振动,飞控舱为运载器传感器及飞控板提供安装位置。其中,由激光雷达得到高度信息,由GPS得到位置信息,由三轴陀螺仪测量运载器的姿态信息。将ROB-PPO(PID)控制器输出的控制力矩通过力矩分配算法得到舵偏角,再映射到与4台涡喷发动机和4个舵机相连的飞控物理输出口,并且将与发动机相连输出口的PWM信号频率调制为400 Hz,与舵机相连输出口的PWM信号频率调制为50 Hz。飞行过程如图12所示。


图12 垂直起降运载器飞行过程Fig.12 Flight process of vertical takeoff and landing vehicle
在飞行过程中,对运载器施加绳子的扰动作用以模拟飞行过程中受到的横风乱流的干扰,并通过Pixhawk的日志记录下运载器的角度信息和角速度信息如图13和图14所示。

图14 飞行过程中俯仰角速度对比Fig.14 Comparison curve of pitch angle regular during flight
图12展示了垂直起降运载器在现实环境下的飞行结果。图13和图14分别是飞控日志记录的俯仰通道的姿态角和姿态角速度的对比曲线,根据飞行过程中垂直起降运载器的飞行状态。对图13和图14中的曲线进行分析,在1~10 s,运载器接收到起飞指令准备起飞,刚开始飞行高度较低,运载器低速上升。在此过程中,主要是弹性振动的干扰作用,可以看出训练的ROB-PPO智能体的控制效果良好。在11~16 s,随着运载器高度的增加,外部阵风对运载器姿态的稳定起到主要干扰作用,同时外部阵风的干扰激起了弹性振动,在此期间扰动增大,因此图13中的曲线呈现波动现象。但是,姿态控制作用下,运载器并没有失稳,之后运载器逐渐下降,姿态角和姿态角速度重新恢复到稳定状态直至着陆。同时可以看出,相较于自适应模糊PID控制,本文研究的ROB-PPO控制方法的效果更好,超调量较小,动态特性和稳态特性较好,说明本设计中的ROB-PPO控制器具有较强的鲁棒性,运载器在垂直起降过程中可以克服一般阵风或者乱流的干扰。
4 结束语
本文中采用ROB-PPO算法设计垂直起降运载器俯仰通道的姿态控制器。仿真结果表明,在考虑弹性振动的条件下,本文设计的深度强化学习控制器的收敛速度和控制性能都优于目前常用的自适应模糊PID控制。设置随机的初始条件训练深度强化学习智能体以及鲁棒观测器对受到干扰的姿态角和姿态角速度的重构作用都是将仿真环境中训练完成的智能体迁移到真实环境的关键。
尽管仿真以及实验结果较好,但是还有很多方面可以优化。比如,观测量和奖励函数,增加飞行信息可以更加准确地描述环境,智能体对于不同的奖励函数有不同的表现。目前已经完成了俯仰通道姿态控制器设计的仿真以及实验验证工作,下一步将考虑运载器在垂直起降过程中的位置控制,其中会涉及故障检测、容错控制。
此外,本文提出的ROB-PPO方法是基于定常模型的,但是可以通过一些方法拓展到时变模型:① 使用递归神经网络(recurrent neural network, RNN):RNN具有记忆功能,能够处理序列数据,并且可以将之前的信息传递到下一个时间步骤中。因此,使用RNN可以在一定程度上适应时变参数模型。② 训练多个模型:在时变参数模型中,可以使用多个模型来表示不同的状态。例如,可以训练一个模型来表示正常工作状态,另一个模型来表示故障状态。然后,在实际控制过程中,根据当前状态的特征选择合适的模型进行控制。
