无人机编队模糊约束分布式模型预测节能控制
2024-03-05郝文康陈琪锋
郝文康, 陈琪锋
(中南大学自动化学院, 湖南 长沙 410083)
0 引 言
固定翼无人机集群协同执行任务已经成为无人机系统应用的重要发展趋势,小型多无人机具有高协同性、多任务、低成本等优势而备受关注[1-2]。无人机编队控制技术作为多无人机协同的子问题得到了广泛研究,无人机编队飞行的目标是通过控制各个无人机的行为以达到理想的队形[3]。
常见的编队飞行策略有主从法、虚拟结构法、基于行为法、共识理论等[4]。无人机编队按照通信方式可划分为集中式和分布式两种[5],集中式方法中通过建立控制中心来实现对整个编队的控制,而分布式方法则是通过相邻个体之间的信息交换来完成整体的编队。因分布式控制不存在控制中心,相比集中式具有更好的灵活性和扩展性。对于编队控制方法,常见的有一致性控制[6]、自适应反馈[7]、滑模控制[8]、模糊控制[9]等,但这些方法不便于处理约束,而使用优化的方法,如分布式模型预测控制(distributed model predictive control, DMPC)可根据具体的需求设计成本函数和约束条件[10-11]。
DMPC是一种在每个采样瞬间求解最优轨迹的反馈控制方法。对该理论的研究,从早期Dunbar[12]和Camponogara[13]等开始至今,已取得丰硕成果,并在无人机领域得到大量应用。Zhou等[10]在非线性模型预测控制框架下,设计了一种无人机无碰撞编队飞行控制器。Zhang等[14]研究了基于自适应差分进化的多无人机编队分布式模型预测控制,实现了多架无人机实时编队保持和避碰。Wei等[15]提出一种改进的DMPC方案,通过在每个智能体的成本函数中加入状态偏差的惩罚项,提高其一致性。Zhou等[16]针对无人机编队问题,提出一种集中和分布式并存的信息交互策略,并基于模型预测控制算法设计了控制律。Hu等[17]基于模型预测控制构建了多无人机协同搜索路径规划模型,并使用粒子群算法对模型进行求解,以提高协同搜索效率。Grafe等[18]针对无人机集群的路径规划问题,设计了一种事件触发的DMPC算法,可降低无人机的计算量和功耗。孙田野等[19]基于分布式模型预测控制,提出基于改进拟仿射类进化方法,以提高无人机编队的集结速度。赵超轮等[11]针对四旋翼编队问题,设计一种分布式模型预测控制器,使得无人机能够在跟踪期望轨迹的过程中快速形成队形。
对于模糊控制问题,Chen等[20]设计一种完全分布式的自适应模糊控制,来解决多智能体系统的全局一致性问题。Rojo-Rodriguez等[21]针对多架四旋翼无人机编队飞行问题,提出一种基于一致性的模糊逻辑增益调度协议。Rezaee等[22]针对无人机主从编队控制问题,设计了模糊逻辑控制对僚机的速度和姿态进行控制。Xu等[23]设计了模糊比例-积分-微分(proportional-integral-derivative, PID)规则的控制器对传统PID的参数进行优化,以提高其控制性能。Tran等[24]通过模糊推理系统自动调整一致性编队控制器的参数,在有限的信息带宽和动态环境条件中实现无人机编队。魏英杰等[25]针对自主水下航行器的控制问题,设计了一个模糊变结构控制器,以提高其鲁棒性。吴正平等[26]针对干扰弹作战问题,提出一种模糊线性/非线性自抗扰切换控制器。
关于无人机编队控制问题,一般研究的是编队的稳定性和可行性,很少有关编队过程中节省能量的研究。对于DMPC算法中的参数设定,增大控制量的权重可减少控制量的作用,但会减缓状态收敛的速率[27-28]。本文考虑在控制量权重不变的情况下,对控制量施加模糊约束来减少控制量的作用,从而达到节省能量的效果。本文使用模糊理论设计对控制量(控制指令)的模糊约束,一方面模糊控制不依赖于无人机的动力学模型,具有鲁棒性[22];另一方面模糊理论根据语言变量值把状态误差分成不同的状态集分别设计控制约束,使得约束更具有针对性和渐变性。如此,当无人机状态误差大时采用较大的指令约束上界,当状态误差小时则采用较小的指令约束上界,使得无人机在不同状态集下都有合适的状态收敛速率。为了验证提出的模糊约束DMPC编队飞行控制器的有效性,使用拉丁超立方抽样(Latin hypercube sampling, LHS)方法与无模糊约束的DMPC算法进行了对比。
1 问题描述
本文采用分布式的编队控制架构,首先选取一架无人机作为无人机编队的长机,负责规划并跟踪路径,然后以长机为起点构造分布式队形,确定各个无人机在编队中的目标点(期望相对位置),最后根据各个无人机与邻居的相对位置误差设计控制器,其中相对误差定义为与邻居之间的相对位置减去期望相对位置。下面是编队控制问题涉及的基本模型。
1.1 单机模型
对于固定翼无人机,其在三维空间中的飞行控制一般采取平面控制和高度控制解耦的形式,为了简化其飞行过程中的动力学参数,本文假设无人机定高飞行,采用了无人机的二维平面运动学模型,其运动学模型[10]为
(1)

对于无人机的控制,采用自动驾驶仪系统对无人机的位置和姿态进行控制,这里只考虑速度和航向角两个回路的自动驾驶仪模型[23,29]:
(2)

同时考虑无人机实际飞行过程中的状态约束,包括速度、加速度、角速度和角加速度:
(3)
式中:Vmin为最小飞行速度;Vmax为最大飞行速度;amax为最大加速度;ωmax为最大角速度;αmax为最大角加速度。

X(k+1)=f(X(k),U(k))
(4)
式中:X(k)和U(k)表示第k时刻的状态量和控制量;X(k+1)表示第k+1时刻的状态量;f(·)是非线性连续函数;X(k)∈X,U(k)∈UX,X为状态空间,UX为指令约束空间,无人机在状态空间的状态变化要满足式(3)的状态约束。
1.2 无人机编队拓扑结构模型
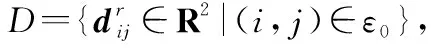
1.3 无人机状态误差模型

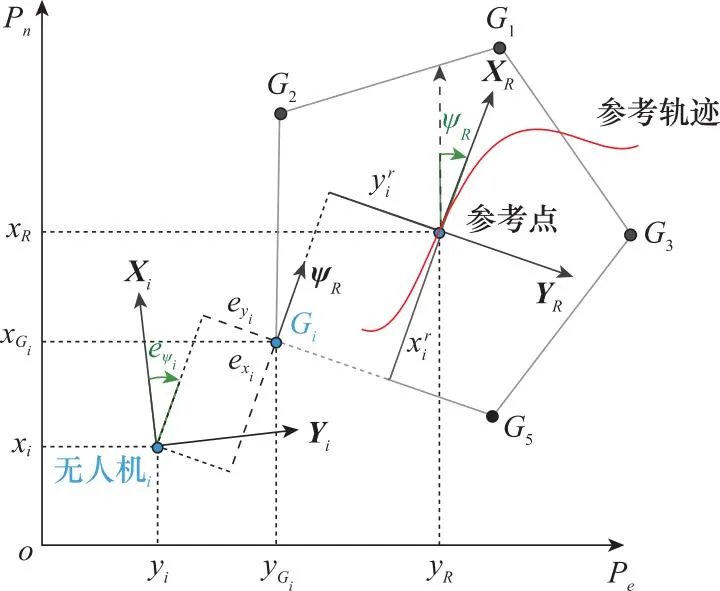
图1 编队飞行示意图Fig.1 Schematic diagram of formation flight
在上述条件下,目标点在PnOPe坐标系中的坐标为
(5)


(6)
(7)
式中:I3×3为3阶单位矩阵,
(8)
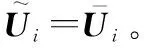
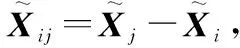
2 编队飞行控制器设计
2.1 模糊约束设计
模糊控制基于启发性的语言决策规则,利用模糊规则来描述系统变量间的关系,适用于对非线性、时变和模型不完全系统的控制,具有较强的鲁棒性、适应性和一定的智能水平。本文通过分析模糊控制的过程获得控制指令的约束,首先对不同的误差状态和控制指令进行语言变量集划分,然后根据模糊规则和模糊推理确定指令输出模糊集的范围,即速度和角度指令的约束范围。设计模糊约束为了减弱参数变化对控制效果的影响,兼顾降低超调和减小收敛时间,减少速度和角度的变化幅度以节省能量。求解模糊约束的过程如下。

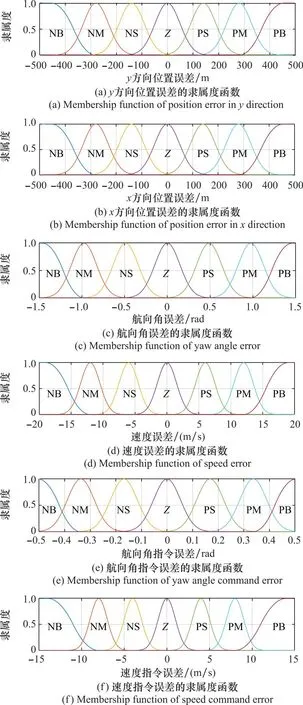
图2 变量的隶属度函数Fig.2 Membership function of variables


表1 航向角指令误差的模糊规则Table 1 Fuzzy rule of yaw angle command error

表2 速度指令误差的模糊规则Table 2 Fuzzy rule of speed command error
最后,确定模糊约束。基于输入和输出变量的隶属度函数及模糊控制规则,输入公式对应的状态量误差,可求出与规则相对应的49个输出模糊集(不同输出模糊集的最大隶属度不同),对不同的输出模糊集进行聚合可以得到聚合模糊集,如图3和图4所示。定义最大输出模糊集为聚合集中最大隶属度对应的元素集合,最优语言值为最大输出模糊集对应的语言变量。对于聚合模糊集的清晰化常用到5种方法,即最大输出模糊集的最小值法Som、中值法Mom、最大值法Lom和聚合模糊集的重心法Centroid、面积等分法Bisector,分别对航向角的输出解模糊,可得到相对应的输出值CSom、CMom、CLom、CCtrd和CBsctr。
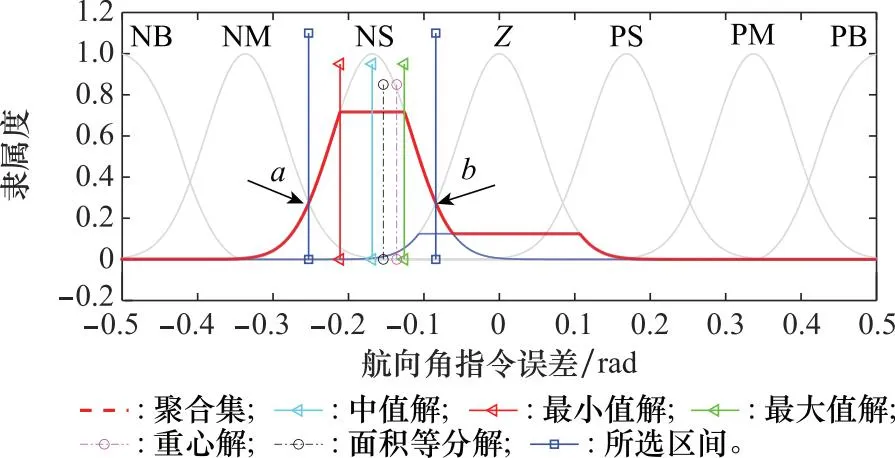
图3 航向角指令的模糊约束Fig.3 Fuzzy constraints of yaw angle command
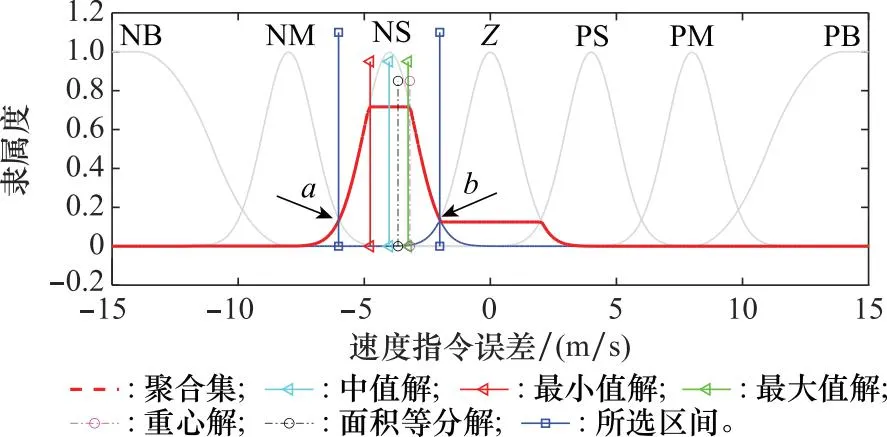
图4 速度指令的模糊约束Fig.4 Fuzzy constraints of speed command

2.2 模糊约束DMPC控制器设计
本节首先介绍DMPC相关内容,DMPC不仅要考虑各无人机与长机之间的状态误差以及控制误差,还需要与其他邻居之间的状态误差;其次,确定模糊约束,虽然每个无人机都和其邻居之间存在误差状态,会产生不同模糊约束,但控制量误差仅和长机相关,所以这里仅考虑通过各无人机与长机之间的状态误差建立模糊约束;最后,把模糊约束添加到DMPC方法中,得到本文提出的模糊约束DMPC控制器。
在用DMPC方法解决分布式最优控制问题中,给定更新周期(或采样周期)δ和预测时域T=δNp,Np为预测的步数。假设分布式最优控制问题可以在tk=t0+δk时刻被瞬时同步解决,其中t0表示初始时刻,tk表示经过k次更新后的实际状态量对应的时刻,其中k∈N。对于分布式模型预测最优控制问题,需要考虑邻居的状态影响,要在每个预测域内对每个无人机的邻居的状态量X-i进行估计。假设对邻居的状态估计满足以下条件:若已知无人机邻居的当前状态量和估计控制轨迹,则可对邻居未来的状态进行估计;在每次更新之前,无人机i可以接受其邻居上一时刻的估计控制轨迹,同时无人机i也会向邻居传输自身的估计控制轨迹。为了方便区分不同情况下的状态和控制,引入下面的符号。相应无人机i在tk时刻的实际状态量Xi(tk)和控制量Ui(tk),定义[11]:

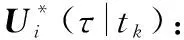
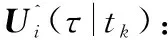
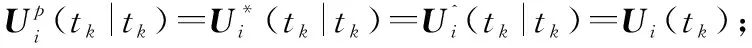
(9)
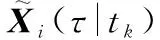
(10)
则可以给出目标函数:
(11)
式中:S(X)和S(U)为归一化矩阵,使状态量误差和控制量误差归一化到[-1,1]区间;M1,M2,N分别为正定对称矩阵,用以保证DMPC算法的稳定性并确定不同的变量所对应的权重[10]。
(12)
式中:κ为任意给定常数;X为状态空间;UX为指令约束空间;UC为模糊约束区间。
虽然传统DMPC算法可以通过增大控制量的权重以降低控制量的作用,但是这样会导致收敛时间变长。而采用具有模糊约束的DMPC算法,在控制量的权重不变的情况下可以降低控制量的幅度变化并使得控制量在一段时间内处于常值状态,以达到降低控制量作用的目的,从而减小能量消耗。模糊约束DMPC算法的描述如算法1所示。

算法 1 模糊约束DMPC算法输入 Xi(t0),X-i(t0),Np,δ输出 最优控制指令U*i(τ|tk)初始化 令tk=t0,对于所有时刻τ∈[tk,tk+T),设U^i(τ|t0)=0和U^-i(τ|t0)=0,t0时刻的控制模糊约束为UC0。步骤 1 根据式(10)求解最优控制指令U*i(τ|tk)。步骤 2 输出U*i(tk|tk)作为τ∈[tk,tk+1)时间段的控制指令。步骤 3 计算所有无人机tk+1时刻的状态量Xi(tk+1)和估计控制量U^i(·|tk+1),为计算tk+1时刻U*i(τ|tk+1)做准备。首先把控制指令U*i(tk|tk)带入无人机单机模型求解tk+1时刻的状态量,其次根据下式求解无人机的估计控制量:U^i(tk+1+δs|tk+1)=U*i(tk+1+δs|tk), s=0,1,…,Np-2U*i(tk+δs|tk), s=Np-1 步骤 4 无人机i把Xi(tk+1)和U^i(·|tk+1)传送给每个邻居,并从邻居处接受X-i(tk+1)和U^-i(·|tk+1)。步骤 5 更新控制指令的模糊约束。步骤 6 令k=k+1,重复步骤1~步骤5。
固定翼无人机的控制可采取水平控制和高度控制解耦的形式,对于高度的控制器设计不会对水平方向的控制产生影响。已知无人机在高度方向的自动驾驶仪为
(13)
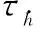
3 仿真验证
为了验证提出的模糊约束DMPC编队飞行控制器的有效性,进行了以下的仿真试验。仿真中考虑6个无人机UAV0~UAV5,其中长机UAV0为编队拓扑结构的参考点,他们的位置坐标、航向角、速度以及相对参考点的参考位置坐标的初始值如表3所示。
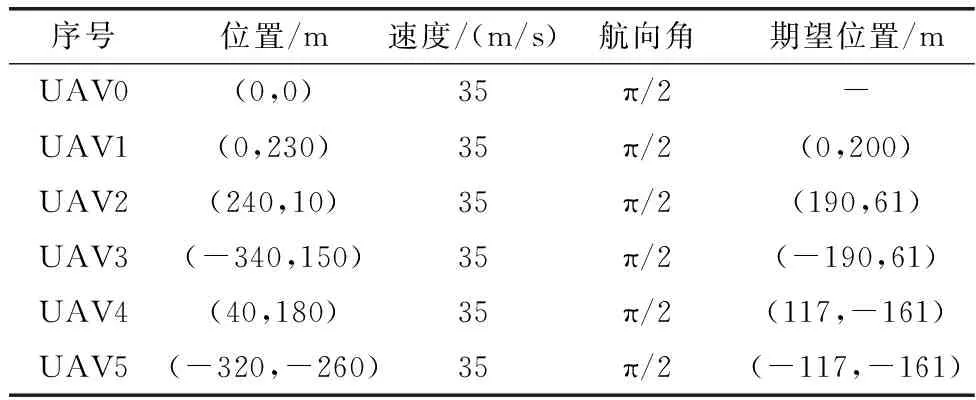
表3 无人机的初始条件Table 3 Initial conditions of unmanned aerial vehicles

仿真试验包含以下两个试验,假设参考轨迹为惯性坐标系下的Pe方向,并且此过程中不考虑外界的干扰。
3.1 DMPC和模糊约束DMPC方法的对比
长机跟踪轨迹,其他无人机根据编队控制算法飞行,比较DMPC算法和具有模糊约束DMPC算法在能量消耗方面的差异。
两种方法产生的飞行轨迹如图5和图6所示,可以观察到每个编队成员不断调整自身位置,以形成期望队形。通过对比可以发现,DMPC算法生成的轨迹会产生较大的波动,而具有模糊约束的DMPC算法在编队形成过程中更为平稳,飞行轨迹较为平滑。
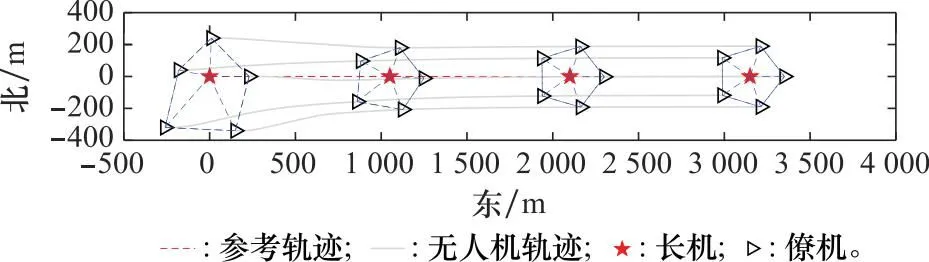
图6 具有模糊约束的DMPC算法生成的飞行轨迹Fig.6 Flight trace generated by DMPC algorithm with fuzzy constraints
对两种方法产生的状态变化轨迹进行对比,如图7所示,图中模糊约束DMPC方法的图例为DMPC&Fuzzy。为了更好地展示仿真效果,选取了位置误差较大的UAV5的状态变化,其中图7(a)和图7(b)展示了无人机在飞行过程中单坐标轴的位置变化,图7(c)和图7(d)展示了无人机飞行过程中速度和航向角的变化。从图7中可以发现以下几点:① 两种方法在相同系数下都可以实现相对位置保持,并且收敛时间差别不大;② 从航向角和速度的变化可以发现,由于DMPC没有考虑模糊约束,会使得航向角和速度在快速达到极值以后迅速远离极值;③ 对于图7(a)中的DMPC算法,无人机在X方向达到合适位置以后,由于速度还未保持一致,导致位置出现超调的情况;④ 而具有模糊约束的DMPC算法,可以使得无人机在飞行的过程中较为平缓的变化,以减少不必要的能量损失。通过对比发现,模糊约束DMPC算法可以减小速度和航向角的变化幅度并起到平稳飞行的作用。
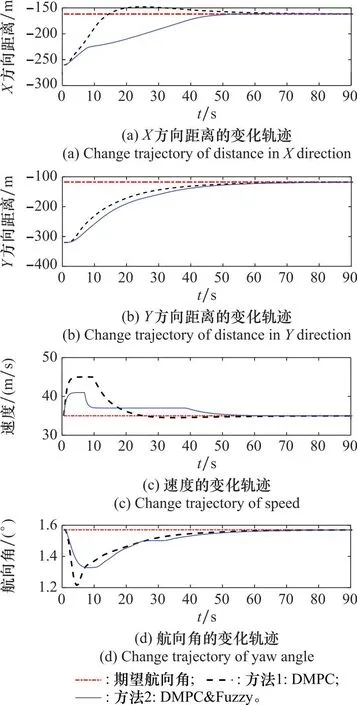
图7 无人机状态量的变化轨迹Fig.7 Trajectory of unmanned aerial vehicles states
为了更好地对两种方法进行对比,定义以下4个对比指标:飞行路程,即无人机从编队开始到结束所飞行的总路程可表示为

(14)
速度变化累计值,即速度改变量绝对值的累加可表示为
(15)
角度变化累计值,即角度改变量绝对值的累加可表示为

(16)
能量损耗,即克服阻力所做的功,由于两种方法的初末状态相同,故采用飞行过程中克服阻力做功来衡量能量的消耗。于是可以得到能量损耗的计算公式[30]为

(17)
式中:阻力和速度的平方成正比Fdrag=KdragV2,假设阻力系数在飞行过程中为常数保持不变,为方便计算,令Kdrag=1。
从具体的数值上进行对比,DMPC方法的飞行路程、速度变化累计值和角度变化累计值分别为3 266.75 m,20.92 m/s,0.71 rad,而具有模糊约束的DMPC算法,其变化分别为3 263.76 m,12.03 m/s,0.48 rad,模糊约束DMPC算法的变化为DMPC算法的99.9%,57.5%,67.6%。对于两种方法的能量损耗变化如图8所示。
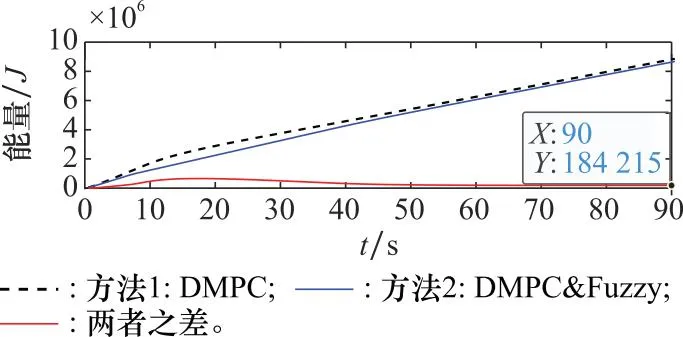
图8 能量损耗的变化过程Fig.8 Change trajectory of energy consumption
从图8中可出,DMPC方法与模糊约束DMPC算法相比,后者克服阻力做功的过程平缓。对于两种方法的能量差值曲线呈现先增大后减小的趋势,对于该结果产生的原因可以结合图7(c)进行解释,刚开始DMPC方法的速度增加较快,克服阻力做功较多,呈现上升趋势;由于DMPC方法的速度增加和下降的幅度大,会在18 s左右的时刻速度达到相同,在之后的时刻,前者速度小于后者,导致DMPC方法克服阻力做功较小,差值曲线呈现降低的趋势,最终趋于稳定;能量消耗差值稳定时,其值大于零,说明模糊约束DMPC方法具有节省能量的优势。
3.2 LHS对比
为了进一步对比模糊约束DMPC算法和DMPC算法,采用LHS方法获取无人机的初始位置,从不同的初始位置出发跟踪编队拓扑结构中的目标点,仿真对比DMPC算法和具有模糊约束的DMPC算法在飞行路程、速度与角度变化累计值和能量消耗的差异。
样本点选取。长机从原点出发沿Pe方向飞行,编队僚机的目标点G在以长机为中心构造出的正五边形顶点上,抽样规则为每架无人机分别以各自的目标点G为中心左右各500 m的范围内抽样1 000次,完成1 000次的编队飞行试验,选取结果如图9所示。
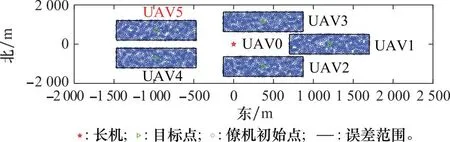
图9 LHS的样本位置Fig.9 Samples location for LHS
图10展示了模糊约束DMPC算法与DMPC算法的对比仿真结果,从单个无人机(以UAV5为例)和无人机编队两个方面对比以下4个指标,即飞行路程之差、速度变化累计值之差、航向角变化累计值之差和能量损耗之差,其差值为DMPC算法减去模糊约束DMPC算法的仿真结果。
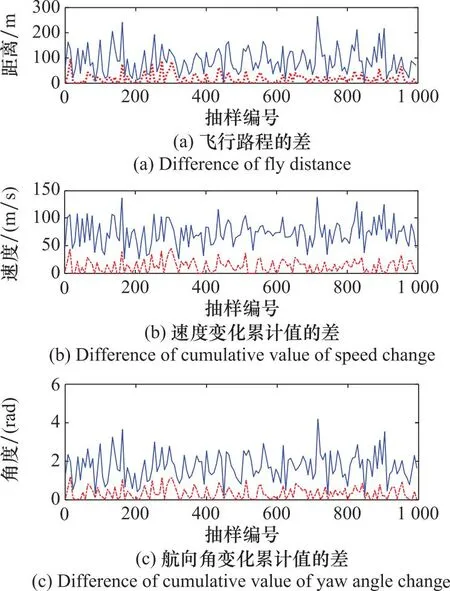
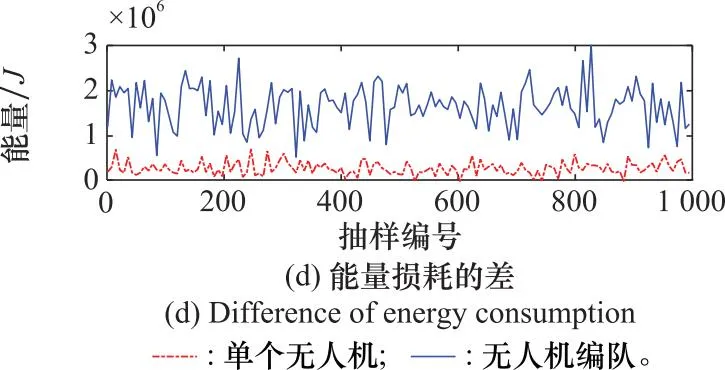
图10 两种控制方法计算结果的差值图Fig.10 Diagrams of difference between the results of two control methods
从图10中可以看出,本文提出的模糊约束DMPC算法的指标(飞行路程、航向角变化累计值和速度变化累计值以及能量消耗)值总体优于DMPC算法;同时若从编队的角度对比两种方法,优势更为明显。
依据4个评价指标,分别从编队飞行试验1 000次和单机飞行1 000×5次的仿真结果进行统计,表4为抽样的统计结果。从表4中的统计结果可以看出:① 由于样本点的初始位置不同但具有相同的初始速度和角度,所以只考虑角度和速度改变的标准差;② 在对编队飞行的统计中可以看出,在每次的仿真实验中本文提出的模糊约束DMPC算法的各个指标都优于DMPC算法;③ 在对单机飞行的统计中,差值小于0的样本点中不仅绝对值小而且占的比例也很小,其中飞行距离和角度改变不足7%,飞行速度不足21%,对于能量损耗差小于0的仅占0.2%,最小值为-42.23,远小于平均值;④ 模糊约束DPMC角度改变和速度改变量的标准差约为DMPC算法的一半。统计结果表明,具有模糊约束的DMPC算法在减少飞行路程、航向角变化累计值和速度变化累计值方面效果明显,同时从标准差可以看出,对于整个样本空间使用模糊约束DMPC算法的速度变化累计值和角度变化累计值的波动较为平缓。
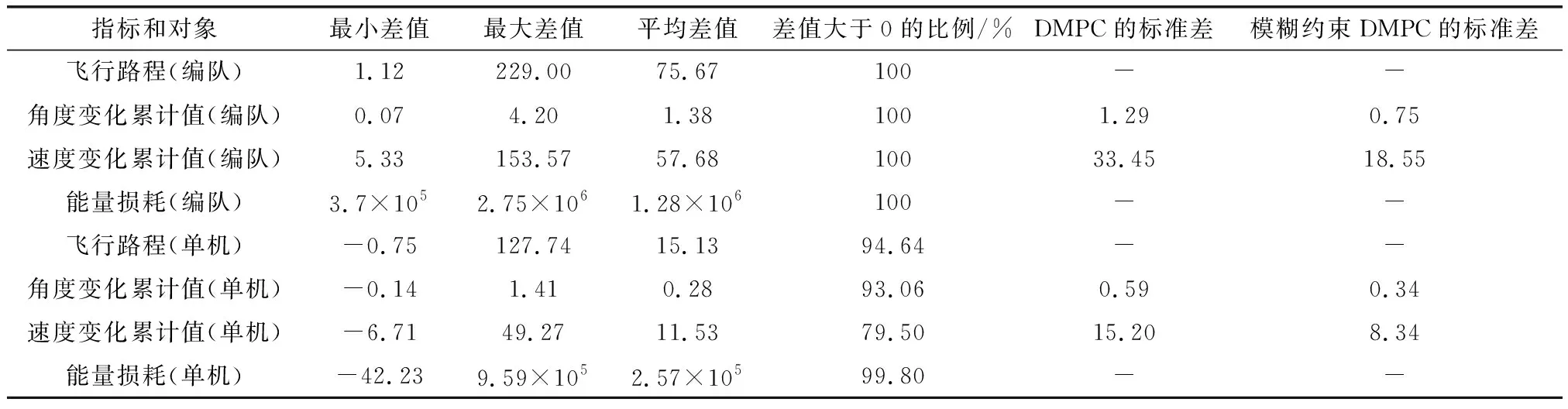
表4 仿真结果统计Table 4 Statistical of simulation results
4 结 论
(1) 把无人机编队中僚机相对长机的状态误差空间进行模糊集划分,并根据定义的模糊规则设计与僚机误差状态相适应的控制指令模糊约束,作为对DMPC控制器的控制量约束,降低了速度和航向角的变化幅度,减少了无人机在编队过程中的能量消耗。
(2) LHS对比仿真的统计结果表明,提出的算法在单机和编队(6架)飞行中节省能量的比例分别为99.8%和100%,从统计意义层面说明该方法在整个样本空间都具有较好的性能优势。
