面向复杂多任务的异构无人机集群分组调配

高 程, 都延丽,*, 步雨浓, 刘燕斌, 王宇飞

(1. 南京航空航天大学航天学院, 江苏 南京 211106; 2. 北京机电工程研究所, 北京 100854)

0 引 言

近年来,无人机作战样式正从单机作战向集群协同作战方向转变[1]。无人机集群分为同构集群和异构集群两种类型,异构集群中各无人机之间功能互补,能力协同,能够适应复杂多样的作战任务需求,逐渐成为集群作战的主力[2-3]。

合理的任务分配是提高异构集群作战系统效能的关键[4]。集群任务分配问题可以看作是复杂多约束条件下的组合优化问题[5-6],随着集群任务规模的增大,作战任务分配问题的求解难度剧增[7]。因此,将大规模集群的任务分配问题进行分解,转化为中小规模问题后再进行求解,能够显著提高任务分配问题的求解效率[8-9]。

大规模任务分配问题的分解[10]包括任务分组和无人机集群分组两个环节,任务分组是无人机集群分组的前提。为了减小分组对全局任务分配的影响,通常按照任务的地理位置进行分组,将地理位置相近的任务聚类为一组,因此任务的分组问题可以采用聚类方法进行求解[11-12]。典型的聚类算法包括基于划分的聚类[13]、基于层次的聚类[14]、基于网格的聚类[15]、基于密度的聚类[16]等。其中,K-means算法是一种应用十分广泛的基于划分的聚类方法,原理简单,计算高效,但是对初始值和噪声十分敏感,容易陷入局部最优[17-18]。文献[19]提出一种基于相异性度量选取初始聚类中心改进的K-means聚类算法,并利用各簇中数据点的中位数代替均值,消除离群点对聚类准确率的影响。文献[20]提出了一种基于K-medoids算法和粒子群优化算法的任务调度技术,用于最小化云计算中的任务完成时间。文献[21]设计了一种加权密度的改进K-means聚类算法,将超密集网络中的毫微微基站划分为不同的簇。

异构无人机集群的分组不同于任务分组,其本质上是一类多对一的双边稳定匹配问题[22-23]。Gale等[24]提出了稳定匹配的概念和延迟接受(deferred-acceptance, DA)算法,用于解决“婚姻市场”中一对一的双边匹配问题,并证明了DA算法所得匹配结果的稳定性。文献[25]针对终端用户和基站的匹配问题,采用基于DA算法的多对一匹配博弈实现网络能效的最大化。文献[26]提出了基于改进DA算法的电动汽车-快充桩匹配策略,通过多轮次算法解决充电服务市场中的多对一匹配问题。文献[27]以异构网络中网络吞吐量和用户性能作为优化指标,提出了一种基于两阶段稳定匹配的动态频谱分配算法。文献[28]提出了一种基于双层稳定匹配的异构无人机集群“分布式”协同算法,将三边匹配问题转化为双层-双边稳定匹配问题进行求解。双边稳定匹配方法应用广泛,并且具有良好的稳定性和最优性,因此可以将稳定匹配的相关方法应用于无人机集群的分组问题中。

本文中设计了一种异构无人机集群按任务进行分组的方法。整个分组的过程分为两个环节,在任务聚类分组环节,首先利用局部密度对目标点样本集合进行离群点检测预处理,通过虚拟目标点替换异常点的方法提高K-means聚类精度。然后,对目标进行固定初始聚类中心的聚类分组,并进行分组均衡性的调整,任务分组完成后计算分组需求的各类无人机的数量。在无人机集群分组环节,运用稳定匹配的思想,对DA算法进行改进,首先基于最优性的考虑,通过任务倾向的偏好列表快速地将无人机映射到匹配度高的分区,然后设计两阶段的冲突消除保证匹配的稳定性和收敛性,得到无冲突的分配方案,完成无人机集群的分组调配。最后,通过仿真实验验证了该方法的有效性。

1 问题描述

本文主要研究复杂多任务下异构无人机集群的分组调配问题,系统模型如图1所示。首先对任务进行聚类分组,然后将无人机集群匹配到任务分组,将目标点任务-无人机集群之间的直接任务分配转化为组内小规模任务分配。假设二维空间的任务区域中存在NT个目标区域T={T1,T2,…,TNT},目标区域是无人机集群执行任务的区域,在分组过程中将其简化为目标点进行处理。每个目标点有多个类型的任务,在分组过程中默认将同一目标点的多个任务分为一组,因此任务聚类分组问题可以等效为目标点聚类分组问题。异构无人机集群U={U1,U2,…,UNV}有多个类型的无人机共NV架,不同类别的无人机携带的载荷资源不同,因此用于执行不同的任务。按照执行任务后是否发生变化将无人机的载荷资源分为消耗型载荷和非消耗型载荷,任务需求一个或多个载荷资源。同一无人机在某时刻只能满足任务的一个载荷资源需求。由此可知,目标点需求某类无人机的数量即为任务需求对应类型载荷资源的数量。为了避免无人机冗余,规定某类任务的载荷需求数量不小于可分配的无人机数量。将目标点聚类后的分组称为分区。

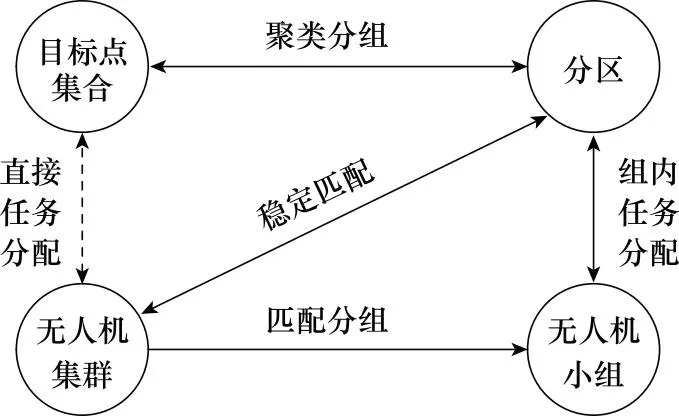
图1 分组调配问题系统模型Fig.1 System model of grouping deployment problem

合理的分组调配能够有效降低任务分配问题的求解难度。以某类需求单个非消耗型载荷的任务为例,假设任务数量为m,可分配的无人机数量为n,分组数量为k,则直接任务分配的解的数量级为nm,分组调配后组内任务分配的解的数量级为(n/k)m/k,分组数量k越大,则二者的数量级相差越大。因此,分组调配可以降低任务分配问题解的数量级,从而提高其求解效率。

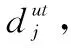
(1)

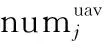
2 目标聚类分组

聚类算法是一种无监督学习,考虑到训练的对象只有目标的坐标值,本文采用改进的K-means聚类方法对目标点进行分组。

2.1 基于局部密度的离群点检测

K-means聚类对异常点比较敏感,为了使最终的聚类效果更加理想,本文首先采用离群点检测算法对目标点样本集进行预处理,将离群点转化为同类型的密集点,然后再对数据集进行聚类分组。根据文献[29-30],离群点具有较大的相对距离和较小的局部密度,因此本文中通过求取局部密度进行离群点检测,算法的相关定义如下。

(1) 第m距离dm(j):目标Tj的第m距离,定义为距离Tj第m远的目标点到Tj的距离,不包括Tj本身。

(2) 第m距离邻域Nm(j):目标点Tj的第m距离邻域,定义为以Tj为圆心,以第m距离为半径的区域内所有目标点的集合,包括第m距离上的目标点。

(3) 第m可达距离reach_dism(i,j):目标点Ti到Tj的第m可达距离表示为

reach_dism(i,j)=max{dm(i),d(i,j)}

(2)

式中:d(i,j)为目标点Ti到Tj的欧式距离。

(4) 第m局部可达密度lrdm(j):目标点Tj的第m局部可达密度lrdm(j)表示为

(3)

即Tj的第m距离邻域内的所有目标点的平均第m可达距离的倒数。

(5) 第m局部离群因子lofm(j):Tj的第m局部离群因子表示为

(4)

即Tj的|Nm(j)|邻域内所有目标点的平均局部可达密度与Tj的局部可达密度的比值。这个比值越接近 1,表明Tj与其邻域点密度相近,Tj可能和邻域同属一簇;这个比值越大于1,表明Tj越小于其邻域点的密度,Tj越可能是离群点。

离群点检测算法的基本流程如下:首先计算每个目标点的第m可达距离和第m局部可达密度。然后,通过局部可达密度得到每个目标点的第m局部离群因子,该离群因子表示目标点的离群程度,因子值越大,离群程度越高,因子值越小,离群程度越低。最后,通过设定离群因子阈值的方式输出密集点集合Ω1和离群点集合Ω2。

2.2 目标点初始聚类分组

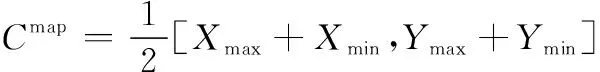
(5)

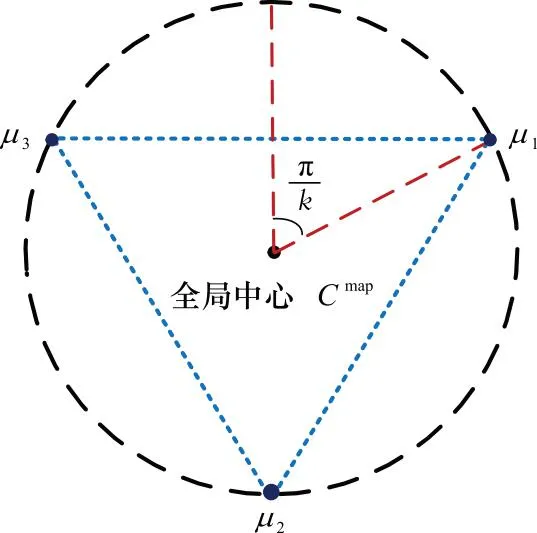
图2 k=3时的初始聚类中心Fig.2 Initial cluster center when k=3

以全局中心Cmap为圆心,设定各分区的聚类中心围绕Cmap均匀分布,编号为i的分区聚类中心的坐标值为

(6)

K-means聚类的优化目标为最小化目标点到所在分组聚类中心距离的误差平方和(sum of squared error, SSE):

(7)

式中:p∈Si为分组Si中的目标;μi=∑p∈Sip/|Si|为分组Si的质心,称为分组的聚类中心。初始聚类算法如算法1所示,在计算得到初始的聚类中心后,分别计算每个目标距离聚类中心的距离,将目标加入到距离最近聚类中心所在的分组。每一轮分组完成后,重新计算新的聚类中心,若更新后的聚类中心发生变化,则重新计算各分区到新质心的距离,循坏迭代访问直到聚类中心不再更新,即完成一次K-means聚类分组。

算法 1 目标点初始K-means聚类分组算法输入 目标点样本集T,初始聚类分组数量k输出 分组聚类中心集合μ,聚类分组划分S1:按照式(5)和式(6)计算初始的k个聚类中心μ2:while flag=1 do3: flag=0;4: for ∀Tj∈T5: 计算目标Tj与各聚类中心的距离列表;6: 选择距离目标最近的聚类中心μi,将目标Tj加入μi的分组Si;7: end for8: for ∀i≤k9: 计算新的聚类中心μ'i=1|Si|∑p∈Sip;10: if μ'i≠μi then11: μi=μ'i;12: flag=1;13: else14: 保持当前分组聚类中心不变;15: end if16:end for17: end while

2.3 分区均衡性调整

初始聚类得到的分区结果可能存在目标数量不均衡的问题,并且在聚类过程中使用了虚拟的密集点集合,因此需要将虚拟的目标点还原为实际的目标点,并进行分区均衡性调整。采用余量表示各分区的目标数量情况,首先根据总的目标数量和分区数量,计算余量基准值nd:

(8)

(9)

在所有分区都为近邻的理想情况下,余量为正表明分区余量充足,可作为转移分区加入新的目标;余量为0表明分区无法加入新的目标,但也无需向其他分区转移目标;余量为负表明目标数量过多,须将多余的目标调整到余量充足的转移分区。而在实际情况下,分区之间可能不存在近邻关系,为了保证分组精度,转移的策略也需要进行调整。分区均衡性调整的相关概念如下:

(2) 转移代价矩阵C:C与M相对应,用于存储目标到分区的转移代价。可转移目标的转移代价为转移前后与分区聚类中心距离的差值,不可转移目标的转移代价为+∞。

算法 2 分区均衡性调整算法输入 未进行均衡性调整的聚类分区S输出 更新后的分区S'1: 计算转移可行性矩阵M和分区余量;2: for ∀i≤k3: ifi<0 then4: 查找分区中能够转移到其他分区的nMi个目标;5: if nMi≠06: for ∀j≤min{nMi,|i|}7: ξ=arg minξCξm,ξ∈Si;8: m=arg minmCξm,ξ∈Si;9: Sm=Sm⊕{Tξ},Si=Si{Tξ};10: end for11: end if12: end if13: end for

K-means聚类和均衡性调整仅依靠目标点的距离关系进行分组,没有考虑到可分配给各分区的无人机数量是否能够满足分区任务的最低需求,因此需要对分组结果进行可行性判断。各分区需求的无人机数量满足一定的区间要求,将此区间表示为[nmin,nmax],区间的上限nmax由分区中所有目标的载荷需求之和决定,区间的下限nmin是分区的最低需求。对于需求非消耗型载荷资源的任务,必须要保证载荷需求最多的任务能够完成,因此区间的下限由分区中单个目标的载荷需求的最大值决定;而对于需求消耗型载荷资源的任务,要考虑单个无人机的最大载荷数量约束,区间的下限要保证所有任务的载荷需求都能得到满足。因此,区间需求的最小无人机数量nmin的计算方法为

(10)

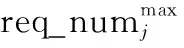
目标聚类分组将分区内的目标点信息传递到聚类中心,改进K-means聚类基于虚拟的密集点集合求解聚类中心,因此聚类中心更加靠近组内的大多数实际目标点,有效避免了离群点的影响。分组均衡性调整可以避免各分区的目标数量相差过大,提高分组的均衡性。通过计算比较无人机数量需求下限与实际可分配的无人机数量,保证当前分组方案的可行性。

3 无人机集群匹配分组

3.1 分区待分配无人机数量计算

在使用聚类分组算法得到目标点的分区后,需要根据分区数量,计算每个分区待分配的某类无人机的数量,各分区待分配的某类无人机的数量Mj的计算方式如下:

(11)

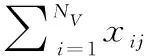
由于式(11)中存在取整运算符,可能导致无人机存在冗余的情况,因此需要调整个别分区的无人机需求数量,保证无人机分组后无冗余。为了提高任务执行的效率,通过计算各分区中无人机的平均负载来判断分区对无人机的需求情况,平均负载较大的分区对无人机的需求更高,因此冗余的名额优先分配给平均负载较大的分区。若存在负载相同的情况,则计算分区的组内平均误差,优先分配给平均误差值较大的分区。

3.2 基于两阶段延迟接受算法的匹配分组

在得到各分区中各类无人机的待分配数量后,需要将无人机集群进行分组,映射到目标分区。每个无人机只能映射到一个分区,同一个分区需要多个无人机,因此将分组问题建模为多对一类型的稳定匹配问题。传统的延迟接受算法在进行多对一稳定匹配时存在一定的局限性,分组的过程由“多”方依据其偏好发起,而后由“一”方根据其偏好选择是否接受,从而得到稳定的匹配结果。在匹配过程中,“一”方只能被动地选择部分“多”方对象,并因此错过自身的最优解,得到的匹配结果容易陷入局部最优。本文中对延迟接受算法进行改进,提出了一种基于两阶段DA(two-phase DA, TPDA)算法的匹配分组方法。

本文中多对一稳定匹配问题的匹配度由无人机的载荷资源种类以及到各分区聚类中心的距离决定。计算各无人机到所有分区的航程代价矩阵E,并对所有分区所需的载荷资源进行匹配,目标Ti与分区Sj的匹配值的计算方法为

即若满足载荷资源要求则将航程代价的倒数作为对应分区的匹配值,不满足载荷要求则将匹配值设为0。在计算得到所有无人机的匹配值后,根据各分区需求无人机的数量对无人机进行匹配。按照每个分区的无人机匹配值大小生成任务倾向的偏好列表,偏好列表中只包含与其匹配值不为0的无人机,且匹配值越大的无人机匹配度越高,在偏好列表中的位置越靠前。结合各分区的载荷需求数量和任务倾向偏好列表,生成预中选方案。任务倾向偏好列表中位于各分区载荷需求范围内的无人机称为“预中选者”,位于各分区载荷需求范围外的匹配值最大的无人机称为“候补中选者”,将各分区的预中选者作为预中选方案的解。

3.3 两阶段冲突消除

预中选方案是每个分区的最优解,但不同分区的任务倾向偏好列表中可能存在相同的预中选者,导致其分配方案之间存在冲突。由于单个无人机只能分配到一个分区,因此定义一个列表match,用来存储无人机的分配情况。冲突消除的流程图如图3所示。

图3 两阶段冲突消除流程图Fig.3 Two-phase conflict resolution flow chart

这个过程分为两个阶段进行,第一阶段将冲突的预中选者替换为候补中选者,以消除当前方案中存在相同预中选者的冲突。具体策略为,若当前分区的预中选者已被分配到其他分区,则比较该无人机在当前分区以及已分配的分区中替换为候补中选者的匹配值之差,选择使用候补中选者代价较小的方案,将对应的预中选者替换为候补中选者,并修正列表match中对应预中选者的已分配分区。由于当前分区的候补中选者可能是其他分区的预中选者,若此类候补中选者成为预中选者,则会再次出现冲突,因此需要多轮冲突消除。冲突消除的过程是将部分分区的最优解替换为次优解的过程,多轮冲突消除可能会使得部分分区资源冗余,导致其他分区的候补中选者不足,无法完成分区任务。通过设置阈值β控制冲突消除第一阶段的迭代次数,若第一阶段结束后不存在冲突,则接受预中选方案作为最终方案,否则仍对预中选方案延迟接受,并进行第二阶段的局部调整。

冲突消除第二阶段局部调整的目的是为了获得可接受的全局可行解,首先对各分区的分配方案进行检测,将存在冲突的分区和未分配的无人机进行回收。对于竞争同一无人机的分区,只有一个分区能够保留原始解,其他分区需要从回收池中选择次优解进行替换。通过计算优先级权值来判断当前分区进行次优解替换的优先级,优先级较高的分区先进行次优解的选择,优先级最小的分区不进行替换,保留原始解。优先级的计算方法为假设当前分区的优先级最高,计算替换前后的匹配值差值,作为计算优先级的权值。权值越小说明替换为次优解后对全局的影响越小,因此权值最小的分区优先级最高,优先进行可行解的选择,已分配的分区和无人机从回收池中移除,不参与下一次的调整。不断重复这个过程,直到竞争同一无人机的分区数量为1,表明冲突的分区都已替换为回收池中的可行解,各分区方案中的冲突已消除,此时接受预中选方案。

TPDA算法的初始预中选方案为各分区的最优偏好,冲突消除第一阶段通过计算预中选者替换为候补中选者的代价,将部分分区的最优解替换为次优解,以消除部分冲突。第二阶段为局部的调整,按照分区的优先级从回收池中选择可行解,直到所有无人机均匹配到唯一的分区。两个阶段均按照最优性原则消除冲突,因此得到的可行解仍是全局最优性较好的匹配方案。

4 仿真验证与分析

本文在典型的异构无人机集群协同执行多任务场景下,通过仿真实验来验证所提出的集群任务分组调配算法的有效性,并与其他算法进行算法性能的对比。仿真平台为具有Intel Core i5-6300HQ 2.30 GHz处理器和8G内存的PC机。

4.1 典型场景下集群分组仿真结果

任务场景设定如下:在50 km×50 km的范围内有20个目标区域,待执行的任务类型共3种,目标区域的参数如表1所示。首先对目标样本进行聚类分组仿真实验,离群点检测的离群因子阈值设为5,分组数量k设为4,余量裕度α设为10%,截断系数dc设为1.35。目标聚类分组前后的对比如图4和图5所示,分组结果如表2所示。从图4中可以看出,聚类算法在离群因子阈值设为5时检测出2个离群点,将离群点替换为虚拟的密集点后,得到的聚类中心更加靠近分组中的大多数目标点,使得后续匹配分组的结果准确性更高。图5中各分区的目标点均位于其聚类中心附近,聚类中心能够有效地代表分区中的目标点,与无人机集群进行匹配。表2中各分区的目标点数量均位于平均值附近,因此在设置的余量裕度范围内,各分组的目标数量基本保持均衡,避免了某些分组的任务分配问题规模仍旧过大,将复杂的大规模问题分解为中小规模问题,有效地提高了任务分配问题的求解效率。在50 km×20 km的区域中随机生成无人机集群,集群中有3种类型的无人机共60架,各类无人机的参数如表3所示。表3中,INF表示非消耗型资源。利用目标聚类分组的结果进行无人机匹配分组仿真实验,TPDA算法的阈值β设为4,得到的TPDA匹配分组的最终结果如表4所示。以匹配结果中出现冲突的无人机数量与无人机总数的比值作为冲突率,为了方便表示,在实际冲突率的基础上加10%作为相对冲突率,得到的预中选结果、经过第一阶段冲突消除的匹配结果、匹配分组的最终结果的冲突率对比如图6所示。

表1 目标区域参数Table 1 Target area parameters

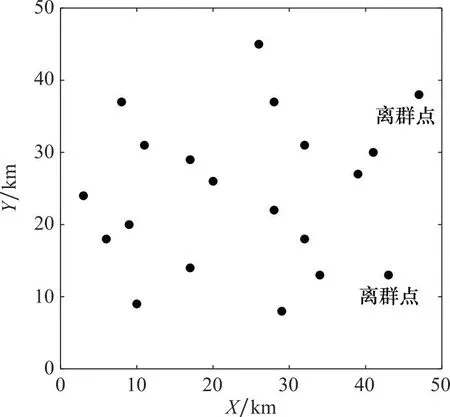
图4 目标聚类分组前示意图Fig.4 Schematic diagram of target clustering before grouping

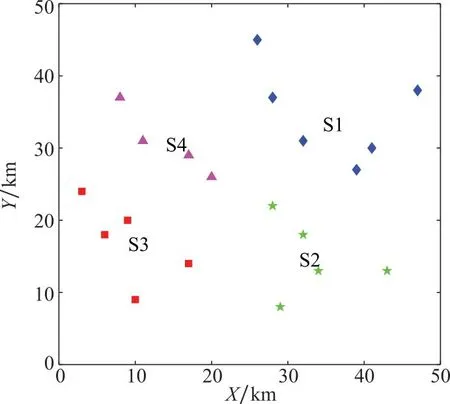
图5 目标聚类分组后示意图Fig.5 Schematic diagram of target clustering after grouping

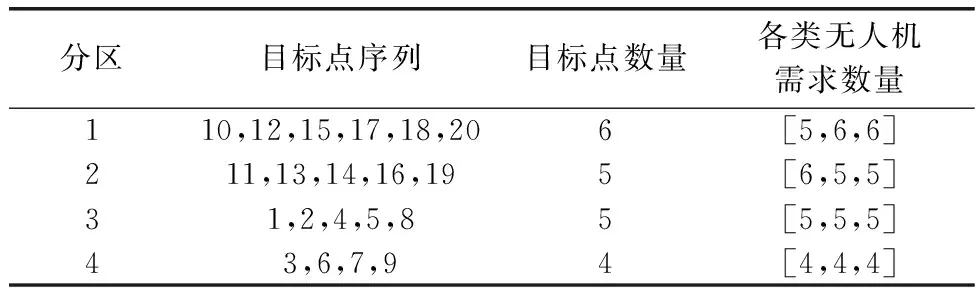
表2 目标聚类分组结果Table 2 Target cluster grouping results

表3 无人机集群参数Table 3 Unmanned aerival vehicle cluster parameters

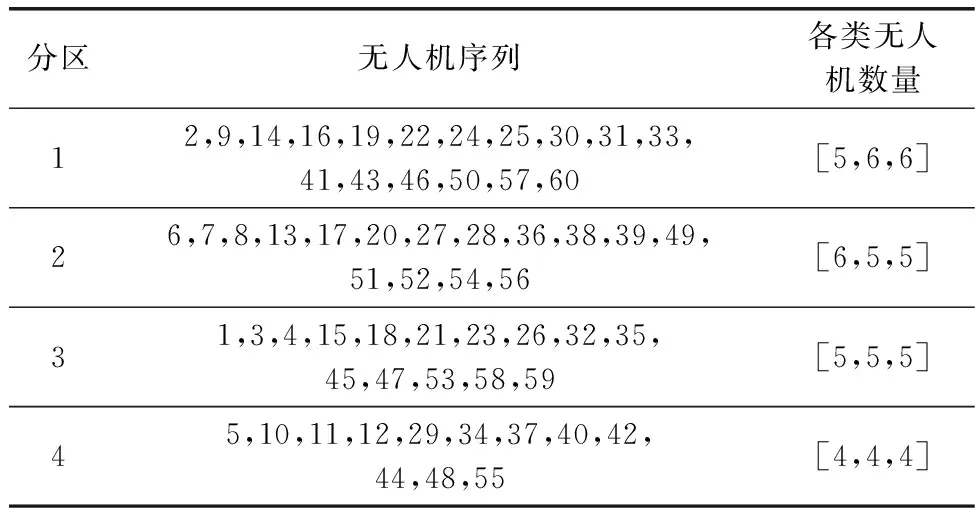
表4 无人机匹配分组结果Table 4 Unmanned aerival vehicle matching grouping results

图6 匹配分组3个阶段冲突率对比Fig.6 Comparison of conflict rates of matching groups in three stages

从仿真结果中可以看出,表4中的匹配分组结果与各分区的需求一致,编号1～60的无人机均对应唯一的分区,因此所提出的TPDA算法能够实现满足分区要求的无人机集群匹配分组,集群中所有无人机均得到了匹配分组,分组结果无冲突。并且,受益于目标分组阶段的负载均衡性调整算法,匹配到各分区的无人机数量比较均衡,各分区待求解的任务分配问题规模基本一致。图6中的预中选结果由于没有经过冲突检测,3种类型任务的冲突率都较高;第一阶段冲突消除按照最优性原则替换部分分区的最优解,因此经过第一阶段冲突消除的匹配结果能够有效地消除部分冲突,在某些情况下甚至能够完全消除冲突,其冲突率明显低于预中选结果;最终结果的冲突率为0%,这说明第二阶段的冲突消除能够完全消除匹配结果中的冲突情况。这是因为第二阶段局部调整的策略是按照优先级依次为仍存在冲突的少量分区从回收池中选择可行解,已选择的无人机从回收池中移除,从而保证匹配的唯一性,消除所有冲突。

4.2 算法性能对比分析

算例 1为了验证所提出的目标聚类分组算法的性能,在50 km×50 km的范围内随机生成30个目标样本点,首先在分组数量k固定为5的情况下进行50次分组的蒙特卡罗仿真实验,与K-means、K-means++算法进行对比,得到的3种算法的SSE性能指标对比图如图7所示,分组结果的目标数量均衡性对比如图8所示,算法的求解耗时对比如图9所示。

图7 SSE性能指标对比图Fig.7 Comparison chart of SSE performance indexes

图8 目标数量均衡性对比图Fig.8 Comparison chart of target quantity balance

图9 聚类算法的求解耗时对比图Fig.9 Comparison chart of time consumption of clustering algorithms

从仿真结果中可以看出,本文中采用的聚类分组算法与另外两种方法的求解耗时基本一致,但分组结果具有更优的SSE值和目标数量均衡性,并且算法的稳定性更高。这是因为K-means算法和K-means++算法没有排除离群点的影响,并且初始聚类中心的选择都具有随机性,导致聚类结果容易陷入局部最优。而本文中的改进K-means算法在分组之前通过离群点检测将目标点样本中的离群点替换为密集点,同时保留了离群点的载荷信息,有效降低了离群点对聚类中心的影响。固定的初始聚类中心提高了算法的求解效率和稳定性,同时分区均衡性调整算法能够对转移代价较小的目标进行调整,在保证最优性的前提下使得分组的结果负载更加均衡。

算例 2为了验证所提出的TPDA匹配分组算法的性能,利用表2中典型场景下的聚类分组结果,按照第4.1节中的参数随机生成无人机集群,设定冲突消除第一阶段的阈值β设为3,进行20次无人机集群匹配分组的仿真实验,将TPDA的匹配分组结果与多对一的DA算法进行对比,得到的平均匹配值对比如图10所示,算法求解耗时对比如图11所示。从仿真结果中可以看出,TPDA算法的平均匹配值比DA算法更高,这是因为TPDA算法以所有分区的最优解为出发点,然后对替换代价较小的分区进行次优解替换,逐步消除冲突寻找可行解。而DA算法按照无人机的偏好发起匹配,分区只能被动地在发起匹配的无人机中选择最优解,容易陷入局部最优,无法保证解的全局最优性。在阈值β设为3时,TPDA算法的求解耗时与DA算法基本一致,因此TPDA算法能够在保证时效性的同时,提高匹配结果的全局最优性。

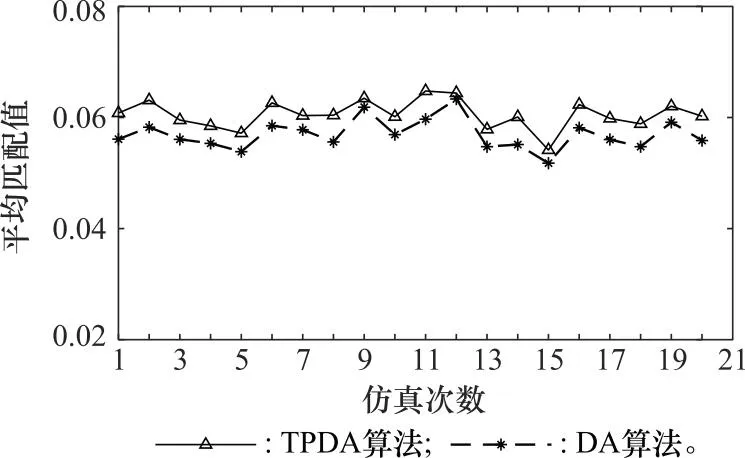
图10 平均匹配值对比图Fig.10 Comparison chart of average matching values

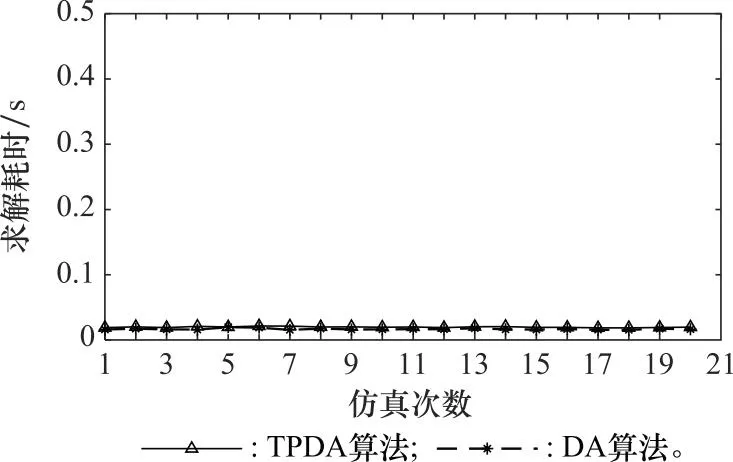
图11 匹配算法求解耗时对比图Fig.11 Comparison chart of matching algorithm solving time consumption

算例 3算例2的仿真验证了无人机集群与聚类中心匹配的最优性,为了进一步地验证所提出的集群分组调配方法的有效性,按照第4.1节中的参数在任务区域中随机生成目标点和无人机集群,进行20次分组调配仿真实验。利用式(1)中的性能指标函数对分组调配结果进行评价,调节系数λ设为0.000 5,将本文中的分组调配方法与采用K-means++聚类和DA算法匹配的方法进行对比,得到的目标函数值对比如图12所示。图12显示,本文所提出的分组调配方法在20次仿真实验中的目标函数值均高于对比方法,分组后的集群完成分组任务的代价更小。因此,改进的K-means算法和TPDA算法能够有效地进行目标聚类分组和集群匹配分组,通过分组调配将大规模的直接任务分配转化为组内小规模的任务分配,提高任务分配问题的求解效率。

图12 分组调配算法目标函数值对比图Fig.12 Comparison chart of objective function values of grouping deployment algorithm

5 结 论

本文中针对异构无人机集群按任务分组调配问题,设计了一种考虑分组均衡性的任务聚类分组方法和提高全局最优性的无人机匹配分组方法。在任务聚类分组环节,首先利用局部密度对目标点样本集合进行离群点检测预处理,通过虚拟目标点替换异常点的方法提高聚类精度。然后,对目标进行固定初始聚类中心的聚类分组,并进行分组均衡性的调整。在无人机集群分组环节,运用稳定匹配的思想,对延迟接受算法进行改进,首先基于最优性的考虑,通过任务倾向的偏好列表快速地将无人机映射到匹配度高的分区,然后设计了两阶段的冲突消除过程,选择对全局最优性影响较小的可行解,保证匹配的最优性、稳定性和收敛性,得到无冲突的匹配分组方案。最后,通过仿真实验分析并与其他方法进行对比,验证了本文所提方法的有效性。