外倾式蝴蝶拱桥拱肋参数影响研究

晏乐群 彭世超

中国市政工程华北设计研究总院有限公司 天津 300074

引言

随着生产力的飞速发展以及科学技术不断进步，人们对桥梁建筑结构的美观要求在逐渐提高。在桥梁美学界，拱桥以其强劲的力度感加之优美的曲线造型，具有较强的艺术表现力，一直受到人们的关注和推崇，同时促进各种造型奇特的异型拱桥的产生。对于外倾式蝴蝶拱桥，目前世界上已经建成的且比较著名的有英国的蝴蝶桥、挪威的罗瑟海斯隧道桥、日本的羽田机场桥等。国内的有广西南宁大桥、广东省中山市蝴蝶拱桥等。虽然国内外建成的异型拱桥有不少实例，但对外倾式蝴蝶拱桥从结构体系上开展的研究相对较少。本文拟通过对某外倾拱桥主要设计参数进行分析，以期更深入地了解该类异型拱桥的结构性能，进行更经济合理的设计。对日益发展的景观异型拱桥的设计有所参考，推动景观桥梁的建设与发展。

1 工程概况及有限元建模

1.1 工程概况

某上跨高速公路主线中承式钢-混结构蝶形拱桥，主体结构由焊接钢管、钢箱组成，拱肋由大直径焊接钢管形成，计算跨度58m。拱肋轴线在同一平面内，其平面与铅垂面呈45°夹角外张。拱肋轴线在其平面内为二次抛物线，高跨比为1／2.8284。

桥面系为纵梁、横梁、小纵梁与现浇混凝土桥面板共同形成的钢-混组合梁，并通过11 对吊杆均匀地作用在两拱肋上。纵梁由16mm厚度的Q345D钢板焊接成箱形截面，并于外侧形成风嘴。顺桥向每隔4m 间距设置一道横梁，横桥向设置3 道通长小纵梁，以保证桥面系整体稳定和局部稳定。横梁、小纵梁均为由Q345D 钢板焊接形成的工字型梁。

桥面板为200mm ～300mm 厚的钢筋混凝土现浇板，并通过横梁及纵梁顶部的焊钉与之连接形成钢-混组合结构。

1.2 有限元模型

采过Midas Civil软件建立有限元模型进行仿真分析，计算模型中拱肋、主梁和桥面板都采用一般梁单元建立，吊杆采用桁架单元建立，结构模型如图1 所示。荷载方面只考虑结构的自重和吊杆初张力荷载。其中钢拱肋和钢主梁的自重考虑结构附属的横隔板、加劲环、铆钉和焊缝的重量而采用1.1 倍自重系数，混凝土桥面板、拱肋内灌注的混凝土和桥面二期的防撞护栏、防落物格栅的重量都按实际重量以梁单元荷载的方式加载。不考虑施工过程，直接计算以上荷载作用下结构的响应。分别改变拱肋倾角及拱肋刚度等参数分析对拱肋受力性能的影响。

图1 Midas 计算模型Fig.1 Midas calculation model

2 拱肋倾角对拱肋受力性能的影响

2.1 模型参数的确定

从外形美观性上考虑，若倾角过小，不能明显体现出外倾式拱肋的特点，若倾角过大，一方面受力情况会更加不利，另外一方面在视觉感受上也会有不安全感。考虑以上因素，共设置7 组对照组，外倾角度分别是25°、30°、35°、40°、45°、50°和55°，所有对照组的拱肋在竖直平面内的投影高度都按1∶4 的矢跨比取为14.5m，各组拱肋在拱肋平面内的矢高按角度关系换算，具体见表1。

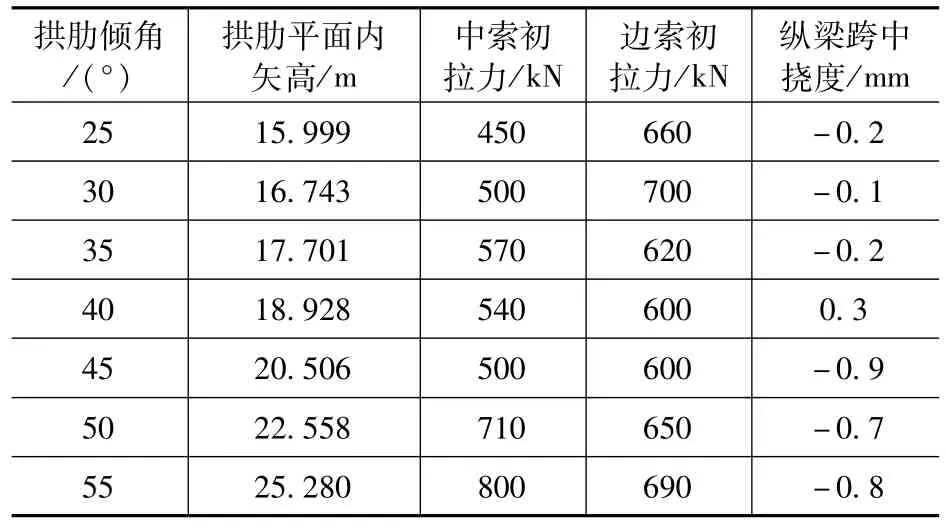
表1 不同拱肋倾角下的拱肋矢高及吊杆张拉力Tab.1 Sagittal height of arch ribs and tensioning force of suspender under different inclination angles

不同拱肋倾角都以调整合理的吊杆张拉力使得主桥跨中成桥变形控制在0 ～-2mm 之间为控制依据，保证主梁的受力及成桥线形尽可能合理。以此为条件，最终确定的各组张拉索力和变形控制情况见表1。

2.2 拱肋倾角对拱肋内力的影响

分析不同拱肋倾角对拱肋结构的最大轴力、拱顶、拱脚竖向弯矩、横向弯矩及最大弯矩的影响，计算结果见图2。

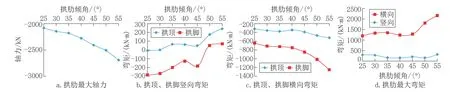
图2 拱肋内力随拱肋倾角变化情况Fig.2 Stress of arch rib varies with inclination angle of arch ribs

从图2a 可以看出，随着拱肋倾角的增大，拱肋的轴力逐渐增大，造成这种变化的原因主要包括以下两个方面：（1）外倾角度增大使得拱肋在自身平面内的矢高增大，由自身重力引起的轴力随之增大；（2）主梁重量一定时，吊杆竖向分力基本不变，随吊杆倾角增大，吊杆最终拉力不断增加，由此引起拱肋轴力的增大。

从图2b 可以看出，随着拱肋倾角的加大，拱顶和拱脚的竖向弯矩都逐渐由负值增大为正值。理想状态下，合理的拱轴线拱肋应是纯受压结构，本桥带吊杆的拱肋弯矩主要是吊杆传递的集中力产生的。随着拱肋倾角的增大，中索拉力增加，拱顶受向下的拉力，正弯矩不断增加；拱脚则是由于边索拉力相对减小而由负弯矩转为正弯矩。

从图2c 可以看出，随着拱肋倾角的增大，拱顶、拱脚的横向弯矩都为负值（内侧受拉）且绝对值不断增大。对于拱脚，拱肋自重产生的横向弯矩占主导地位，随着拱肋倾角增大，拱肋自重的力臂增加，拱脚的内侧受拉程度不断加大。对于拱顶，拱肋自重使其横向受弯产生的弯矩很小，而吊杆对拱肋的拉力使其内侧受拉，拱肋倾角增大，拱顶附近吊杆拉力不断加大，拱顶内侧受拉程度不断加大。基于以上分析可以得出，拱顶和拱脚的横向受弯程度随着拱肋外倾程度的增大而迅速增大，当倾角较大（大于40°）时对拱肋的整体受力有重要的不利影响。

从图2d 可以看出，随着拱肋倾角的增大，拱肋中出现的竖向弯矩最大绝对值变化规律不明显，拱肋主要受压，竖向弯矩主要受吊杆力影响，通过合理的调索，弯矩可以控制在较低的水平，对拱肋应力影响较小。对于拱肋横向最大弯矩，拱肋倾角在45°以下时，弯矩值在1200kN·m到1400kN·m 之间波动，而当拱肋倾角达到50°或更大时弯矩值迅速增加。根据各组的横向弯矩图得出最大弯矩均发生在拱肋四分点下方灌注混凝土的区域，且均为外侧受拉。主要因为混凝土的重量相比钢管拱肋大很多，在其自重作用下这一区段向外侧斜下方变形而外侧受拉，其程度随拱肋倾角而增大。而吊杆拉力使拱肋向内侧变形，该区段内侧受拉，其程度随吊杆力增大而增大，即随拱肋倾角而增大。两种相反方向的作用相互抵消，但前一种占主导地位。倾角增大到50°或更大时，吊杆使拱肋向内侧受拉已不足以抵消拱肋混凝土自重下产生的外侧受拉，使得横向弯矩迅速增大。

2.3 拱肋倾角对拱肋应力的影响

从图3 可以看出，随着拱肋倾角的增大，拱肋最大应力总体呈上升趋势，在拱肋倾角30°到45°之间基本上稳定在70MPa左右，倾角超过50°以后应力水平激增，一方面是因为轴力在稳定增加，另一方面是因为拱肋最大横向弯矩已经激增至一个比较高的水平。从图3 反映的结果来看，拱肋倾角45°及以下时拱肋的应力水平都是比较合适的。

图3 拱肋最大应力随拱肋倾角变化情况Fig.3 The maximum stress of arch rib varies with inclination angle of arch rib

2.4 拱肋倾角对拱肋变形的影响

比较不同拱肋倾角对拱肋变形的影响，由于各对照组的拱肋在自身平面内的矢高不相同，单纯绝对值的比较并不能准确地反映出拱肋的变形水平。因此把变形的绝对值除以各组拱肋平面内矢高，得到拱肋相对变形值作为考察指标。计算结果见图4。

图4 拱肋变形随拱肋倾角变化情况Fig.4 Deformation of arch rib varies with inclination angle of arch rib

从图4 中可以看出，随拱肋倾角的增大，拱肋竖向变形的变化趋势比较明显，相对变形一直在增大，倾角超过45°后，相对变形增大速率加快。拱肋横向的相对变形则规律性并不明显，各组总体差别不大，倾角为45°时相对变形百分比最小。综合拱肋横向和竖向变形分析的结果可以得出，拱肋的变形总体上随拱肋倾角的增大而增大，在倾角超过45°以后，相对变形达到了较高水平。

2.5 拱肋倾角对拱肋稳定性的影响

从图5 可以看出，不论是恒载单独作用下还是恒载与活载共同作用下，结构的一阶失稳特征值都随着拱肋倾角的增大而减小，说明拱肋倾角越大，拱肋自重作用对整体稳定性的不利影响越大，结构失稳的可能越大。在最不利的拱肋倾角55°的情况下，恒载加活载的特征值为10，仍然满足规范要求，说明本桥的整体稳定性良好。

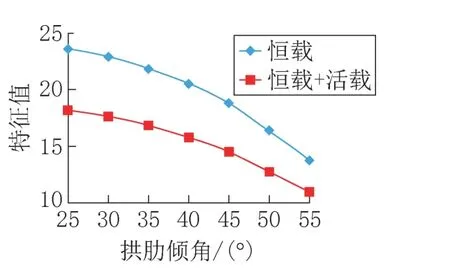
图5 结构一阶失稳特征值随拱肋倾角变化情况Fig.5 The first order instability eigenvalue of the structure varies with inclination angle of arch rib

3 拱肋刚度对拱肋受力性能的影响

3.1 模型参数的确定

设置6 个对照组，拱肋直径分别为0.8m、0.9m、1.0m、1.1m、1.2m、1.4m。规定直径0.8m的拱肋的刚度为EI，计算得到其余对照组的拱肋刚度见表2。除了拱肋直径不同以外，六组方案其他参数全部保持一致，拱肋倾角取为45°。

表2 拱肋直径与相对刚度对照Tab.2 Comparison of arch rib diameter and relative stiffness

将主梁跨中成桥变形控制在0 ～-2mm 之间，以此为条件，最终确定的各组张拉索力和变形控制情况见表3。

表3 不同拱肋直径的对照组吊杆张拉力情况Tab.3 Tensioning force of suspension rods in control groups with different arch rib diameters

3.2 拱肋刚度对拱肋内力的影响

分析不同拱肋刚度对拱肋结构的最大轴力、拱顶、拱脚竖向弯矩、横向弯矩及最大弯矩的影响。计算结果见图6。

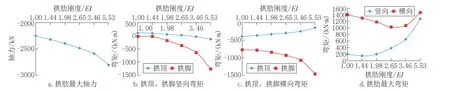
图6 拱肋内力随拱肋刚度变化情况Fig.6 Stress of arch rib varies with stiffness of arch rib

从图6a 可以看出，随着拱肋刚度的增加，拱肋承受的压力逐步增加。拱肋刚度增加使得梁-拱组合体系中拱肋分担的荷载比例增加，造成拱肋轴力加大。拱肋轴力增大的速度远小于拱肋刚度增加的速度，拱肋刚度增大5.5 倍时，最大轴力只增大了25%。主要原因是拱肋轴力主要由主梁的荷载产生，虽然拱肋分担的荷载比例增加了，但荷载总量增加的程度并不大。

从图6b 可以看出，随着拱肋刚度的增大，拱脚处的竖向弯矩迅速增大，且刚度越大，增大速度越快。因为本桥采用的部分灌注混凝土的无铰拱在自重作用下拱脚产生负弯矩，随着拱肋刚度的加大，拱肋自身的重力在拱肋所承担的荷载中的比例不断加大，负弯矩逐渐增大。拱顶弯矩在刚度较小时是正值，随着刚度增加而逐渐减小变为负值，总体来看，拱顶弯矩都不大，对拱肋受力的影响较小。主要因为拱肋刚度较小时，吊杆传递的主梁自重荷载占主导地位，拱顶受到吊杆向下的拉力而产生正弯矩。而拱肋刚度较大时，拱肋自重产生的弯矩占主导而产生负弯矩。

从图6c 可以看出，随着拱肋刚度的增加，拱脚的横向弯矩为负值（内侧受拉）且绝对值逐渐增加，拱顶的横向弯矩为负值（内侧受拉）且绝对值逐渐减小，最终变为正值。通过受力分析得出，在拱肋自身重力作用下，拱肋向外侧弯曲，拱脚内侧受拉而拱顶外侧受拉。在由吊杆传递的主梁重力作用下，拱肋向内侧弯曲，拱脚外侧受拉而拱顶内侧受拉。拱肋刚度较小时，拱肋自重也较小，近拱顶部分吊杆力的作用占主导而内侧受拉，随着拱肋刚度增大，拱肋自重增加，其产生的弯矩逐渐平衡拱顶处的负弯矩，使拱顶逐渐变为外侧受拉。对于拱脚，在本次分析取到的拱肋尺寸范围内，拱肋自重产生的横向弯矩占主导地位，拱脚一直内侧受拉，并随着拱肋尺寸加大，弯矩值逐渐增加。

从图6d中可以看出，当拱肋直径在1m以下时，拱肋中出现的最大竖向弯矩都较小，并且通过实际计算的拱肋弯矩图得知，此时拱肋竖向弯矩分布比较均匀。随着拱肋直径继续增大，拱肋中出现的最大弯矩迅速增加，因为此时拱肋自重在拱脚处产生的负弯矩已成为整个拱肋的控制弯矩，说明仅从控制拱肋竖向弯矩的角度来看，此时拱肋截面选取已经过大。拱肋尺寸较小时，拱肋出现的最大横向弯矩较大，这一弯矩主要是由主梁荷载产生的。随着拱肋尺寸的增大，拱肋自重的作用逐渐平衡主梁荷载的作用，拱肋最大横向弯矩逐渐减小，当拱肋直径超过1.1m 后弯矩又转为增大，此时拱肋自重起控制作用。

3.3 拱肋刚度对拱肋应力的影响

从图7 可以看出，拱肋应力随刚度的增加逐渐减小。本桥拱肋轴力作用对应力的贡献比例比弯矩作用大，随着拱肋刚度的增大，轴力增长较缓慢。同时，拱肋不论是截面面积还是抗弯刚度都迅速增加，导致拱肋应力逐渐减小。

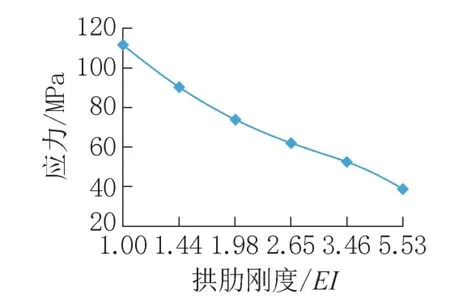
图7 拱肋最大应力随拱肋刚度变化情况Fig.7 The maximum stress of arch rib varies with stiffness of arch rib

3.4 拱肋刚度对拱肋变形的影响

从图8 可以看出，随着拱肋刚度的增大，拱肋的最大变形（在拱顶处）不论是在竖向还是在横向都迅速减小。除了拱肋直径0.8m 时拱肋变形稍大以外，另外几组的变形都在比较合理的范围内。

3.5 拱肋刚度对拱肋稳定性的影响

从图9 中可以看出，拱肋刚度与特征值基本呈线性关系，不论是恒载单独作用下还是恒载与活载的共同作用下，结构的一阶失稳特征值都随着拱肋刚度的增大而增大。拱肋刚度由EI变化到5.53EI时，恒载作用下结构稳定特征值增大2倍，恒载与活载共同作用下结构稳定特征值增大1.85倍。因此增加拱肋的刚度，对于增强结构的稳定性效果非常明显。

图9 结构一阶失稳特征值随拱肋刚度变化情况Fig.9 The first order instability eigenvalue varies with stiffness of arch rib

4 结论

1.拱肋的总体受力随拱肋倾角的加大而变得更为不利，当倾角大于50°时拱肋受力及变形急剧增加。但拱肋倾角的变化，并不影响拱肋屈曲形态，均为拱肋面外屈曲失稳；结构的一阶失稳特征值随着拱肋倾角的增大而减小，且减小的速率随着倾角增大而增大。结合外观上的考虑，倾角在35°到45°之间时，拱肋外倾的特征不仅能够明显的表现出来，并且受力较为合理。

2.改变拱肋刚度参数，研究对称外倾蝴蝶拱拱肋的内力、应力、变形及稳定性情况，拱肋直径0.9m到1.1m 时拱肋的受力较为合理，应力和变形水平都比较适中，弯矩分布也相对均匀。随着拱肋刚度的增大，拱肋变形迅速减小，当拱肋刚度小于2 倍的设计值时，拱肋变形降低效率较高。结构的一阶失稳为拱肋的面外失稳，并且结构一阶失稳特征值都随着拱肋刚度的增大而增大。