埋地压力管道在敷设方向改变时考虑曲管段侧向约束的受力分析

郭巍 蒋杰 周晨

南京市市政设计研究院有限责任公司 210018

引言

埋地压力管道在敷设方向改变处、截面变化处和管道端部位置会产生推力。在水平面敷设方向改变时，节点处产生的推力由管道内的静水压力以及动水压力两部分组成。因为大多数管道内的液体在相对较低的速度下运行，所以动水压力在计算推力时通常被忽略不计。为满足节点处稳定性要求，目前国内外采用的措施主要有：在节点处设混凝土侧向支墩、沿管长方向设置混凝土拖拉墩、桩基础以及依靠管道周围土的约束力等。在实际工程中，对于在大中型城市主城区建设的大口径、高内水压力的压力管道，依靠设置支墩来抵抗管道转角处的水平推力存在着较大困难，无法在管道转角处设置支墩的工程，通常采用将管道整体连接的方式，依靠管-土的摩擦力和管侧被动土压力来抵抗转角处的水平推力，即所谓的无支墩设计［1］来抵抗管道水压推力；也可采用结合曲管段约束与管道刚性连接的方式共同作用来抵抗水平推力，该曲管段约束包括有：在曲管段处使用压实度更高的回填土、设置支墩或者灌注桩基础。

刘雨生［2］总结了国内外无支墩埋地压力管道敷设方向改变时的两种设计模式，一类是只计入纵向摩擦力，另一类是除纵向摩擦力外尚计入了土体对管道的侧向抗力，该分析模式未考虑曲管转角段的约束。《给水排水工程埋地钢管管道结构设计规程》（CECS 141：2002）［3］给出的约束长度计算公式中，未体现出直管段土的侧向抗力对约束长度的影响，式中也没考虑曲管段的侧向抗力的影响。日本“土地改良事业计画设计基准”给出钢管的计算模式［4］是考虑管道纵向摩擦力与管道侧向土壤抗力的共同作用抵抗管道的水平推力，对于曲管段土的有利作用，运用了朗肯被动土压力公式计算得到，且是在总推力中直接扣除该被动土压力，未考虑曲管段约束与直管段约束共同作用对管道内力分布的影响。美国水业协会标准（AWWA-M9—2008）［5］给出了刚性连接的混凝土压力管道无支墩设计的有效约束长度计算，同样是考虑了管侧横向土抗力和轴向摩擦力的共同作用来抵抗管道水平推力，对于曲管段土的抗力计算采用了温克尔地基模型，但考虑曲管段和直管段的横向土侧向刚度一致。ASCE 埋地管道的推力约束设计任务委员会［6］针对连续型管道理论提出了在AWWA-M9—2008 公式的基础上增加了管道弯曲应力和轴向应力的求解来对模型进行修正。文献［7］考虑了横向土壤抗力和纵向管道的与土壤间摩擦力共同作用，给出了刚性接口、柔性接口和自锚式接口下的管道约束长度的解析计算公式，同样也未考虑曲管侧向约束对计算约束长度的影响。

本文主要基于欧拉-伯努利梁理论和温克尔地基梁模型［8］，推导了直管段轴向摩擦力和横向土抗力、曲管段侧向约束共同作用下的管道有效约束长度的解析解，对比研究了是否考虑曲管段范围土的侧向刚度对管道的内力、位移的影响，分析了管-土摩擦系数、敷设方向改变角度、直管段土侧向刚度、曲管段侧向约束等因素对管道约束长度、弯矩、轴向力和剪力的影响。该分析有助于可靠且充分利用管道周边土壤的约束力，通过合理设计曲管段侧向约束（曲管段支墩、灌注桩基础、高密实度回填土）以减小管道约束长度。

1 埋地压力管道的受力分析

1.1 简化分析模型

在埋地水平面上敷设方向改变的压力管道，管道外径D，管道内径D0，管道水平转角为Δ，水平推力为T，曲管段侧向支撑刚度为K，直管段土的侧向刚度为k，k应综合考虑管道两侧土压力，且符合温克尔弹性地基梁模型，直管段有效约束长度为Lb，假设曲管段为刚体，直管段采用不考虑剪切变形的欧拉梁理论。埋地压力管道的简化分析模型如图1 所示。

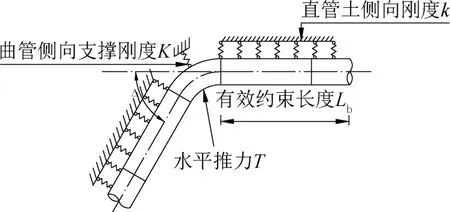
图1 埋地压力管道分析模型Fig.1 Analysis model of pipe of buried pressure pipeline

1.2 直管段受力分析

如图2 所示，曲管段与直管连接处的节点轴力、剪力和弯矩分别为F0、V0和M0，直管段管道任意一点轴力、剪力和弯矩分别为F、V和M，管段单位长度摩阻力为fμ，δx为直管段约束长度范围在管起始端的累计轴向变形，δy为直管段约束长度范围在管起始端的横向变形。

图2 埋地压力管道直管段的受力分析Fig.2 Stress analysis of buried pressure pipeline straight pipe section

对其在X方向受力平衡，∑X ＝0 得到：

在Y方向受力平衡，∑Y ＝0 得到：

化简式（1）和式（2）得到：

对管道微元体顶部中心（o点）的力矩平衡，∑Mo＝0 得：

忽略高阶无穷小项，并对式（5）进行一阶微分得：

根据欧拉-伯努利梁理论公式：

将式（3）、式（4）、式（7）代入式（6）得：

式（8）四阶微分方程的特征方程为：

式（9）的特征方程有两对共轭的复数根，其实数部分和虚数部分的绝对值相等：

因此，式（9）的一般解为：

式中：系数C通过边界条件求解得到。

对于刚接接口的管道，曲管和直管之间的转角为零；当x→∞时，管道的横向位移为零，即：

将式（12）代入式（11）得：

将式（13）代入式（11）得到直管段的侧向位移方程为：

令v＝0，可以得到如下解：

令x＝0 时，曲管与直管连接处的剪力V0、弯矩M0如下：

1.3 曲管段受力分析

不考虑管道液体流速的影响，管道在水平转角处的推力为：

式中：P为管道内水压；A＝πD20／4。

根据力的平衡分析得出：

式中：K＝k′lb，曲管段的侧向约束可使用压实度更高的回填土、支墩或者灌注桩基础来提供曲管段支撑刚度K。管侧若采用回填土，lb为曲管在垂直合力T方向上的投影长度，lb＝2Rsin（Δ／2），R为曲管段的曲率半径，k′为曲管段范围内土的侧向刚度；若管侧采用支墩或者灌注桩基础，lb为支墩或灌注桩承台在垂直合力T方向上的投影长度，k′为曲管段范围内土的等效侧向刚度，如图3 所示。

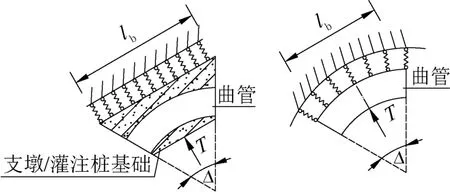
图3 埋地压力管道曲管段的侧向约束示意Fig.3 Analysis diagram of lateral constraint for curved pipe sections of buried pressure pipelines

取曲管段作为隔离体，如图4 所示，曲管段位移为δ。

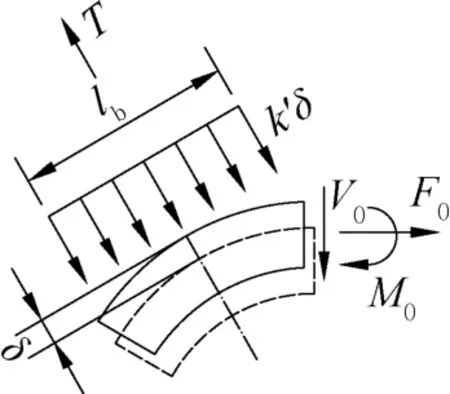
图4 埋地压力管道曲管段的受力分析Fig.4 Stress analysis of curved sections of buried pressure pipelines

1.4 变形协调条件

由于方程（14）并不能直接求出，须通过直管与曲管连接处位移满足变形协调条件求解，如图5 所示，即：

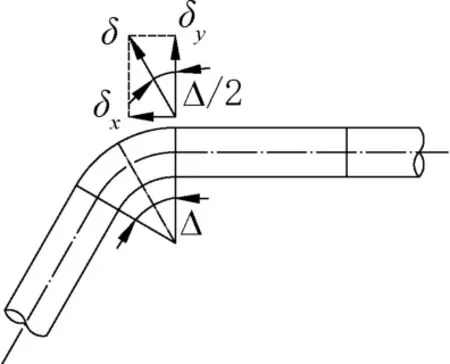
图5 直管与曲管连接处位移的变形协调Fig.5 Deformation coordination of displacement at the connection between straight pipes and bent pipes

1.5 联立求解

假设单位长度承受的摩擦力fμ是常数，且管道能够承担剪力和弯矩，则有效约束长度（该有效约束长度是仅为了抵抗直管段的轴力）为：

单位长度摩阻力［7］如下：

式中：μ 为管道与土的摩擦系数；γs为土的容重；Hs为管顶覆土；γw为管道内液体容重。

文献［7］给出了直管段约束长度范围在管起端位置的累计变形δx如下：

式中：Ap为管道截面面积。

令式（14）中的x＝0，可得到δy如下：

将式（23）、式（24）代入式（20）得：

将式（25）代入式（19），化简得：

式（26）为一元二次方程，令：

根据求根公式求得方程的解：

求出F0后，代入式（25）、式（17）和式（21）即可求出直管起端位置的剪力、弯矩和有效约束长度。

2 算例分析

管道计算基本参数如下：管道外径D取2.288m，壁厚取0.024m，管道水平转角为45°，曲管段在合力T方向上的投影长度为lb取为1.470m，弹性模量为E取2.0 ×108kN／m2，管道内液体重度γw取为10kN／m3，水压P为0.68MPa，土的重度γs取为18kN／m3，管道与土的摩擦系数μ取为0.25，地下水位位于管道底以下，管顶覆土Hs为4m，直管段土的侧向刚度k取为20000kN／m2，曲管段土的侧向刚度k′取为20000kN／m2。

由图6a 可知，考虑曲管段土侧向刚度将会减小直管段的最大位移；直管段的侧向位移零点始终保持不变，距离直管段起始点为3π／4λ1，且仅受直管抗弯刚度和直管段土侧向刚度的影响。

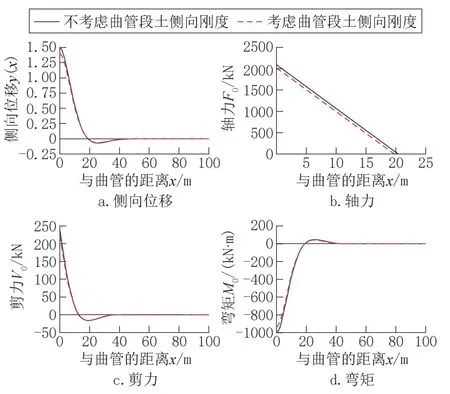
图6 是否考虑曲管土侧向刚度对直管段的影响Fig.6 Comparison of straight pipe sections whether considering the lateral stiffness of curved pipe soil

由图6b可知，考虑曲管段土侧向刚度将会减小直管段最大轴力；沿着管长方向，轴力逐渐减少，减少速率保持不变，且轴力减少速率仅和单位长度的摩阻力相关；当轴力为0 时的直管段长度即为管道的有效约束长度。

图6c、d可得出考虑曲管土侧向刚度将会减少直管段的剪力和弯矩，且从直管起端开始，沿管长方向曲管土侧向刚度的影响逐渐减少。

以上分析可以看出，考虑曲管段土侧向刚度将会减小直管段的侧向位移、内力，但是影响有限。若要增大影响，可采用灌注桩或支墩。

3 参数分析

为了研究直管段土侧向刚度、曲管段侧向约束、管-土摩擦系数、敷设方向角度改变对直管段有效约束长度、弯矩、轴向力和剪力的影响，取管道计算基本参数如下：管道外径D取2.288m，壁厚取0.024m，弹性模量E取2.0×108kN／m2，管道内液体重度γw取为10kN／m3，水压P为0.68MPa，土的重度γs取为18kN／m3，地下水位位于管道底以下，管顶覆土Hs为4m。

3.1 直管段土侧向刚度、曲管段侧向约束的影响

如图7 所示，曲管内力、位移δ和约束长度Lb都随着曲管段范围内土的等效侧向刚度k′的增加而减小，这表明了通过使用更压实的回填土或支墩来增加曲管段土侧向刚度将有益于减小约束长度和内力。

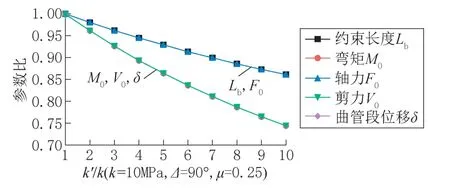
图7 等效侧向刚度k′对内力、 位移和约束长度的影响Fig.7 The influence of equivalent lateral stiffness k′ on internal forces，displacement and constraint length

正如图4 和式（19）所示，弯曲处的推力由三个分量抵抗，即剪切力V0、轴向力F0和曲管段侧向支撑反力k′δlb，图8 所示给出了不同的等效侧向刚度k′对三个分量占总推力比值的影响。当k＝k′时，曲管段的侧向支撑承载总推力的2%，直管段承担其余推力，这些推力随后被管道沿线的土壤消散。将弯曲处的有效土壤刚度增加到其原始值的10 倍后，即k′＝10k，弯曲处的侧向支撑承担了总推力的16%以上。土壤刚度的变化将影响每个约束系统所承受推力的百分比。因此，通过考虑总推力的固定百分比来设计每个约束系统是不安全的。为了实现两个系统的均匀可靠性水平，建议通过适当选择土壤刚度比，在两个约束系统之间分配推力。

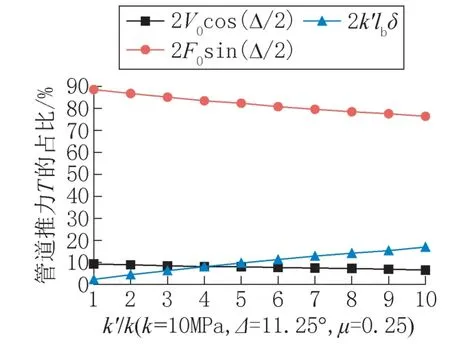
图8 不同等效侧向刚度k′下的各分力的占比Fig.8 The proportion of each component force under different equivalent lateral stiffness k′

3.2 管-土摩擦系数的影响

管-土摩擦系数取决于许多因素，如管道材料、表面粗糙度、回填类型及其压实水平和地下水位等。如图9 所示，增加摩擦系数是有利的，因为弯矩M0、剪切力V0、曲管段位移δ 和约束长度Lb随着摩擦系数的增加而减小，然而，轴向力F0随着摩擦系数μ 的增加而增加，这可能需要更厚的壁或弯曲附近的更多纵向加强件。

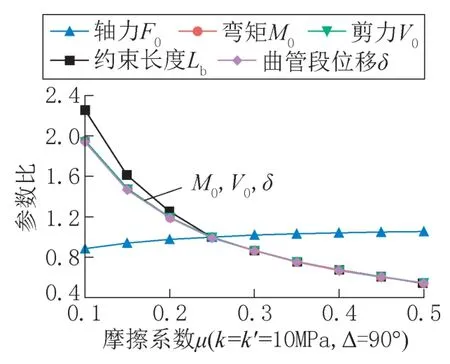
图9 摩擦系数对曲管段内力、位移和约束长度的影响Fig.9 The influence of the friction coefficient on internal force，displacement of curved pipe section and constraint length

3.3 敷设方向角度改变的影响

如图10 所示，随着敷设方向改变角度的增加，轴向力F0、约束长度Lb逐渐增加，弯矩M0、剪力V0和曲管段位移δ先增大后减小。这表明对于较大的角度改变，曲管段位移δ 的增加主要归因于较大的轴向力引起的轴向位移的增加，且直管侧背后土体侧向刚度影响越来越小。

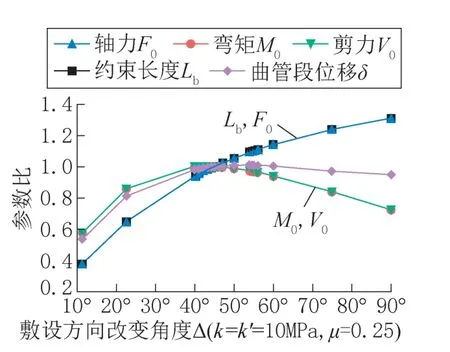
图10 敷设方向改变角度对曲管段内力、 位移和约束长度的影响Fig.10 The influence of change in angle of the laying direction on the internal force，displacement of curved pipe sections and constraint length

如图11 所示，曲管位移δ 在Δ ＝54.3°处达到峰值，然后减小；横向位移δx在Δ ＝43°处达到峰值，然后减小，而轴向位移δy随着弯曲角度的增加而单调增加。根据变形协调条件，Δ ＝90°弯曲的横向位移和轴向位移始终相等。

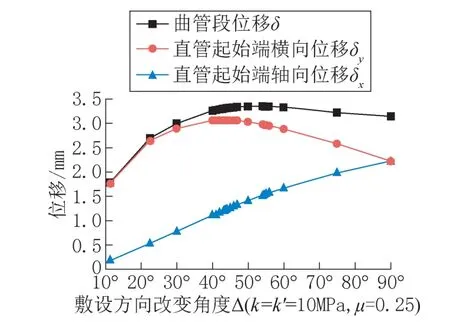
图11 敷设方向改变角度对曲管段位移的影响Fig.11 The influence of change in angle of the laying direction on the displacement of curved pipe sections

4 结论

本文基于欧拉-伯努利梁理论和温克尔地基梁模型，推导了直管段轴向摩擦力和侧向土抗力、曲管段侧向支撑共同作用下的直管段有效约束长度的解析解，分析了直管段土侧向刚度、曲管段侧向约束、管-土摩擦系数、敷设方向改变角度等因素对管道约束长度、弯矩、轴向力和剪力的影响。主要结论如下：

1.使用更压实的回填土或支墩来增加曲管段侧向支撑刚度将有益于减小约束长度和内力。通过在管道敷设方向处设置支墩或增强曲管段土的性质，对于这种双约束系统来计算有效约束长度时，约束刚度的变化将影响每个约束系统所承受推力的百分比，通过考虑总推力的固定百分比来设计每个约束系统是不安全的。

2.随着摩擦系数的增加，曲管段弯矩、剪切力、曲管段位移和有效约束长度逐渐减小，然而，轴向力随着摩擦系数的增加而增加，这需要更厚的管壁或弯曲附近的更多纵向加强件。

3.随着敷设方向改变角度的增加，曲管段节点处轴向力、有效约束长度逐渐增加，曲管段弯矩、剪力和曲管段位移先增大后减小；直管起始端横向位移先增加后减小，而直管起始端轴向位移随着弯曲角度的增加而一直增加。这表明对于较大的角度改变，曲管段位移的增加主要归因于较大的轴向力引起的轴向位移的增加，且直管侧背后土体侧向刚度影响越来越小。