煤矿巷道七自由度喷浆机器人轨迹规划与跟踪控制

程欢， 邓立营

（沈阳工业大学 化工装备学院，辽宁 沈阳 110000）

0 引言

煤矿巷道的常见支护方式为喷锚支护，喷浆工作是喷锚支护的重要施工环节。在巷道施工中喷浆工作通常采用人工或人与机械相结合的方式。巷道施工环境恶劣，工作强度大，施工效率低，回弹率高，质量可控性差，因此应用自动化喷浆机器人是实现煤矿巷道高效、安全喷浆施工的重要途径[1]。

国内外对机器人工作臂轨迹规划与运动控制开展了大量研究。在轨迹规划方面，通常采用插值法、时间最优等轨迹规划算法实现工作臂的直线运动或圆弧运动。在运动控制方面，一般根据控制需求设计工作臂的控制系统，将算法与系统相结合，得到满足需求的工作臂最优运动控制。邓稼敏等[2]对六自由度锚护机器人进行分段式轨迹规划，求得在最短时间运动到达终点的工作臂轨迹。刘送永等[3]采用环境网络法对喷浆机器人工作臂轨迹进行规划，得到较优的运动轨迹和运动参数。肖振楠等[4]采用4-3-4 多项式关节插值算法，对六自由度机械手进行轨迹规划。Liu Gangfeng 等[5]提出了八自由度喷浆机器人工作臂轨迹规划方法，并在实际巷道中进行实验。Chen Gang 等[6]应用时间最优轨迹跟踪控制算法对冗余工作臂末端执行器进行研究，获得时间最优的轨迹。Liu Yibo 等[7]针对满足Pieper 准则的六自由度工作臂提出了一种工作子空间划分方法，有效避免了由于大量的逆解选择问题导致的工作臂关节突变和轨迹错位，使规划的轨迹平滑。刘俊辉等[8]为解决液压工作臂关节存在的响应迟滞问题，提出了一种基于三次B 样条函数的轨迹纠偏算法。谢斌等[9]对八自由度喷浆机器人工作臂进行轨迹规划及控制系统设计，实现工作臂自主工作。许万等[10]针对移动机器人轨迹跟踪问题，设计了带有干扰观测器的混合控制器，并用Lyapunov 函数直接法证明了系统的收敛性和稳定性。Yang Libo 等[11]采用模型预测控制（Model Predictlve Control，MPC）算法对轮式移动机器人进行跟踪控制，实现了移动机器人多输入多输出系统的精确控制。H. Cheon 等[12]提出了未知复杂动态环境中移动机器人的高效实时局部运动规划算法，实现在状态-时间-空间中逐步进行轨迹规划。

煤矿巷道环境复杂，喷浆机器人工作过程中存在动作不连续、位置误差大、稳定性差等问题。因此，本文提出了煤矿巷道七自由度喷浆机器人轨迹规划与跟踪控制方法。根据煤矿巷道喷浆施工要求，对巷道进行截面划分；设计喷浆机器人在巷道截面间的移动轨迹和各截面上工作臂运动轨迹，提升喷浆机器人动作的连续性；采用多项式插值法生成喷浆机器人移动轨迹和工作臂运动轨迹，通过MPC 算法对喷浆机器人移动轨迹进行跟踪控制，提高喷浆机器人移动的准确性和平稳性。

1 喷浆机器人轨迹规划与跟踪控制

1.1 喷浆机器人结构

喷浆机器人由移动底盘、工作臂和喷枪组成，如图1 所示，其中移动底盘采用轮式结构，包括平台和基座，工作臂包括大臂、小臂和腕部。

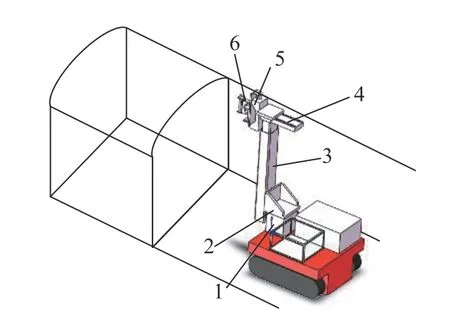
图1 喷浆机器人组成Fig. 1 Composition of shotcrete robot

喷浆机器人工作臂由7 个关节组成，关节间采用串联的结构形式，如图2 所示。工作臂采用液压驱动，可以实现平台旋转、基座旋转、大臂伸缩、小臂伸缩、腕部旋转、腕部伸缩、末端喷枪自转。

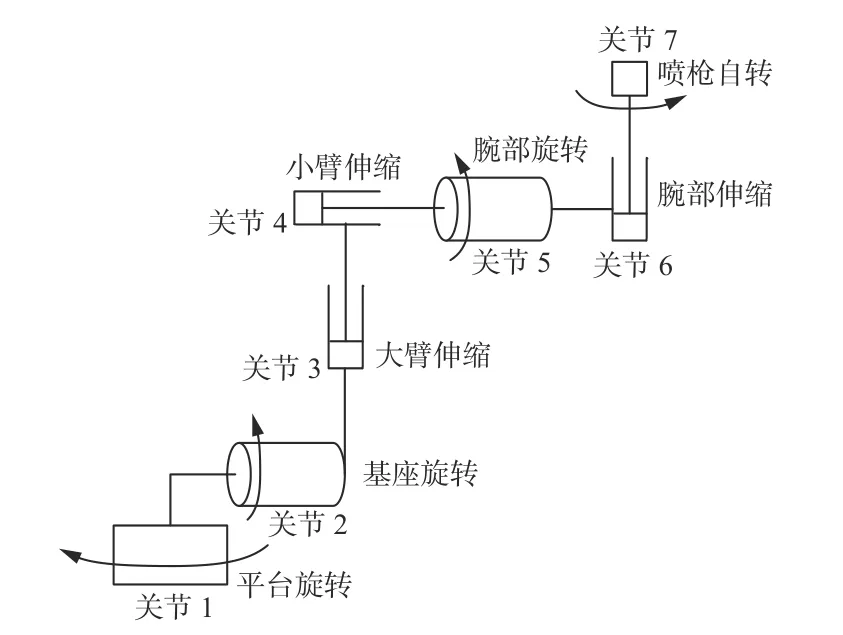
图2 工作臂关节设置Fig. 2 Working arm joint setup

工作臂自由度为

式中：m为关节数；Pl为低副数量；Ph为高副数量。

本文中Pl=7,Ph=0，根据式（1），该喷浆机器人的工作臂具有7 个自由度。

1.2 喷浆机器人轨迹规划

参考GB 50086—2015《岩土锚杆与喷射混凝土支护工程技术规范》，喷射作业应分段分片进行[13]。根据喷浆机器人静止时工作臂的运动范围和喷枪沿巷道走向的喷浆长度，将煤矿巷道沿走向划分为n个截面。喷浆机器人在巷道中的轨迹如图3 所示。喷浆工作开始时，喷浆机器人由起点沿巷道走向移动到巷道待喷截面n-1 后，工作臂沿轨迹A→D运动，喷枪实施喷浆工作；工作臂移动到D后保持静止状态，由移动底盘控制机器人移动到截面n，该过程中机器人移动轨迹为D→E，同时喷枪处于喷浆状态；机器人运动到截面n后，工作臂沿轨迹E→H运动，喷枪实施喷浆工作。

图3 喷浆机器人在巷道中的轨迹Fig. 3 Trajectory of shotcrete robot in roadway

将喷浆机器人完成巷道内任一截面喷浆工作的过程定义为1 个工作周期（如机器人沿D→E→H移动完成截面n喷浆为1 个工作周期）。在1 个工作周期内喷浆机器人工作流程如图4 所示。先对喷浆机器人移动轨迹进行规划，机器人沿轨迹移动时，对机器人移动轨迹进行跟踪控制；机器人到达喷浆位置后，对工作臂轨迹进行规划，由工作臂驱动喷枪完成喷浆工作。机器人的移动轨迹规划和工作臂轨迹规划在每一个工作周期内交替进行，以保证喷浆机器人喷浆动作的连续性。

图4 喷浆机器人工作流程Fig. 4 Work flow of shotcrete robot

1.3 喷枪机器人运动学模型

建立喷浆机器人运动学模型，如图5 所示。{w}为巷道坐标系，其中x轴为机器人前进方向，y轴垂直于x轴指向巷道壁面；{q}为机器人移动坐标系，其中xq，yq轴与x，y轴方向相同。当机器人处于转向状态时，令左侧轮的坐标系为{l}，其中xl轴与xq轴方向相同，yl轴垂直于xl轴指向左侧巷道壁面；令右侧轮的坐标系为{r}，其中xr轴与xq轴方向相同，yr轴垂直于xr轴指向右侧巷道壁面。 θ为机器人方向角；φ为xq轴与y轴间的夹角；2L为底盘宽度。

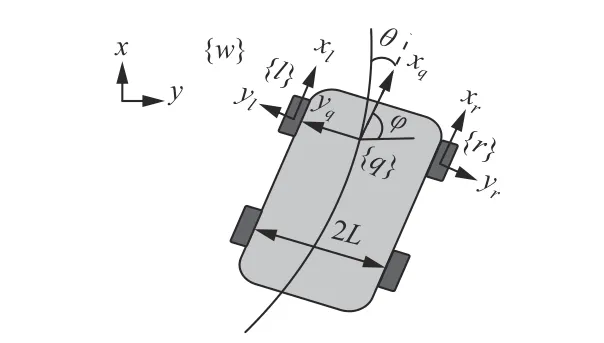
图5 喷浆机器人运动学模型Fig. 5 Kinematics model of shotcrete robot

机器人左右侧轮在机器人移动坐标系{q}下的位置分别为

在机器人移动坐标系{q}中，机器人的运动方程可表示为

式中：v(t)为机器人在移动坐标系{q}下的速度，t为时间；ω(t)为角速度；vl(t)，vr(t)分别为机器人左右侧轮在移动坐标系{q}下的速度。

移动底盘控制机器人移动时，在车轮轴线的投影方向上，车轮速度分量为0，即

机器人在式（2）和式（3）约束下的无侧向移动非完整数学模型为[8]

式中：z(t)为机器人移动状态，z(t)=[x(t)y(t) θ(t)]T；u(t)为机器人控制量，u(t)=[v(t) ω(t)]T。

为描述机器人控制效果，定义机器人移动过程中的位置误差为

式中：Xc(t)为机器人理想位置；X(t)为实际输出位置。

1.4 基于MPC 算法的轨迹跟踪控制

喷浆机器人移动轨迹跟踪控制步骤：先采用三次多项式插值进行轨迹规划，再通过MPC 算法对三次多项式插值生成的参考轨迹进行跟踪控制。通过设计合适的控制量u（t），使得机器人在预测时域内[14-16]实现参考轨迹的跟踪。给定参考轨迹为

式中 β0— β3为多项式系数。

机器人的控制输出Yc(t)和约束输出Yb(t)分别为

式中：gc（·）为控制输入；gb（·）为约束输入。

机器人控制量和输出的约束为

式中：umin(t)，umax(t)分别为控制量的最小值和最大值；Ybmin(t)，Ybmax(t)分别为约束输出的最小值和最大值。

为得出机器人轨迹预测跟踪的最佳控制输入，即预测输出与期望输出越接近越好，定义预测输出与期望输出之间的累计误差为目标函数J，引入惩罚后的目标函数为

式中：Np，Nc分别为预测时域和控制时域，且满足Nc≤Np；i=0，1，···，Nc-1 ；γ(·)为期望控制输出；Q，R为加权矩阵，可以是时变的；u¯(·)为预测的控制量；uk(·)为输入的参考控制量；u¯i为当前输出控制量。

寻找最佳输入可描述为如下的优化问题：

求解式（16）可归结为求解非线性规划问题，通过序列二次规划（Sequential Quandratic Programming，SQP）求解器进行求解[17]。

2 喷浆机器人工作臂轨迹规划

2.1 喷浆机器人工作臂运动学模型

喷浆机器人采用七自由度工作臂对煤矿巷道进行喷浆作业。以工作臂相邻关节轴线的公垂线和关节轴线交点为原点，关节轴方向为z'轴，公垂线的指向为x'轴，y'轴由右手法则确定，建立工作臂各关节坐标系。利用标准的D-H 参数法[18-19]，由各关节坐标系间的变换获得工作臂的连杆参数，见表1。 Ωj为连杆长度， αj为连杆扭转角，dj为连杆偏距， ϑj为关节角。对于转动关节j， ϑj为关节变量，其他3 个连杆参数固定不变；对于移动关节，dj为关节变量（可用来表示关节位移），其他3 个连杆参数固定不变。

表1 工作臂D-H 参数Table 1 D-H parameters of working arm

其中：

通过工作臂关节的变换矩阵，由已知关节的角度、位移能够得到工作臂相对于煤矿巷道的位姿[20-21]。

2.2 3-5-3 分段多项式插值轨迹规划

对于任意巷道截面工作臂运动轨迹，给定轨迹上的4 个轨迹点并将运动轨迹分为3 段，如图6 所示（以截面n-1 为例，A，B，C，D为4 个轨迹点）。对轨迹A→B和C→D采用三次多项式插值，对轨迹B→C采用五次多项式插值，通过3-5-3 分段多项式插值轨迹规划使工作臂在喷浆过程中具有连续的加速度。

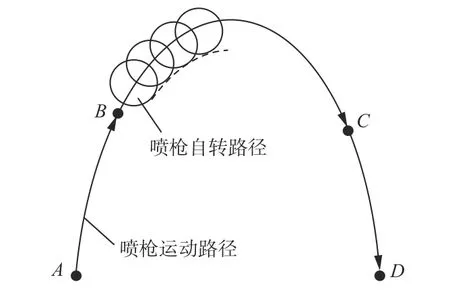
图6 喷枪参考轨迹Fig. 6 Airbrush reference trajectory

A→B段关节j的运动轨迹Sj1与喷浆时间t1的关系：

B→C段关节j的运动轨迹Sj2与喷浆时间t2的关系：

C→D段关节j的运动轨迹Sj3与喷浆时间t3的关系：

式中fj10，fj11，···，fj14，fj20，fj21，···，fj25，fj30，fj31，···，fj34为多项式系数。

3 仿真验证

根据喷浆机器人移动及工作臂运动的要求，利用Matlab/Simulink 搭建喷浆机器人轨迹规划与跟踪控制仿真系统。当机器人处于初始状态时，输入机器人初始位置，系统预测下一段时域的位置输出，然后控制机器人到达输出位置。机器人完成移动后，输入工作臂液压系统的驱动信号，驱动工作臂沿巷道截面轨迹完成喷浆工作。为模拟煤矿巷道复杂环境，在系统中引入2 个随机干扰，选用Simulink 中的阶跃信号随机作用于机器人移动过程。

机器人位置跟踪曲线如图7 所示。可看出机器人在巷道内的实际跟踪轨迹与参考轨迹重合，机器人移动过程中的最大位置误差为0.07 m，误差较小，满足巷道内机器人移动精度要求。机器人方向角跟踪曲线如8 所示。可看出机器人移动过程中的实际方向角和参考方向角曲线大致重合，二者差值较小，最大差值仅为0.99 rad，表明机器人移动时具有较好的稳定性。

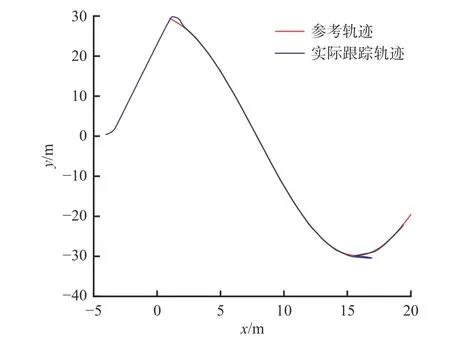
图7 机器人位置跟踪曲线Fig. 7 Robot position tracking curve

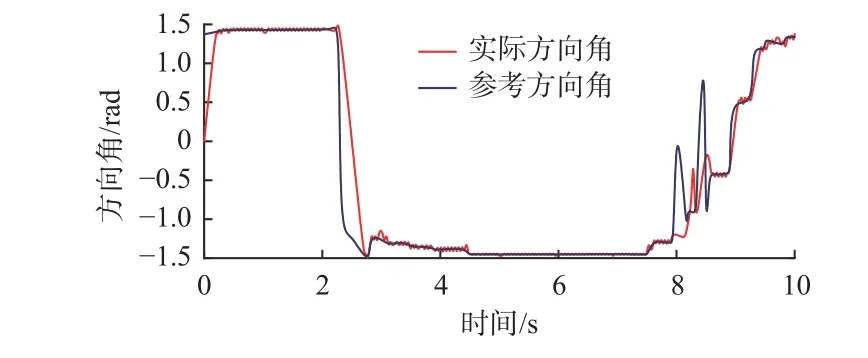
图8 机器人方向角跟踪曲线Fig. 8 Robot direction angle tracking curve

机器人移动速度控制曲线如图9 所示。可看出机器人移动速度总体稳定在10 m/s，速度发生波动后能在较短时间内回到稳定运动状态，表明MPC 算法满足巷道内机器人平稳移动控制要求。工作臂运动轨迹如图10 所示。可看出轨迹点间由圆滑的曲线连接，表明喷浆轨迹稳定、平滑，能够满足巷道喷浆施工要求。

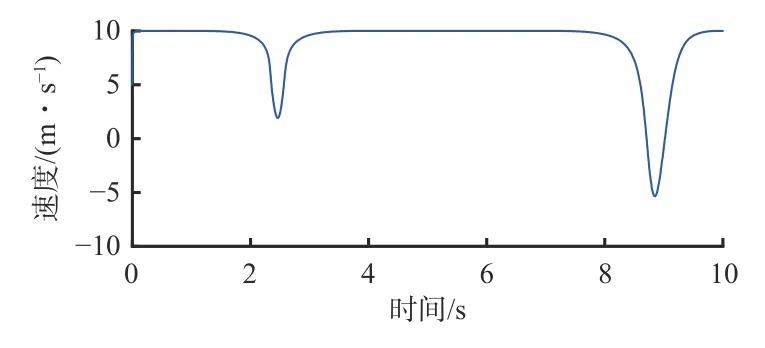
图9 机器人移动速度控制曲线Fig. 9 Robot moving speed control curve

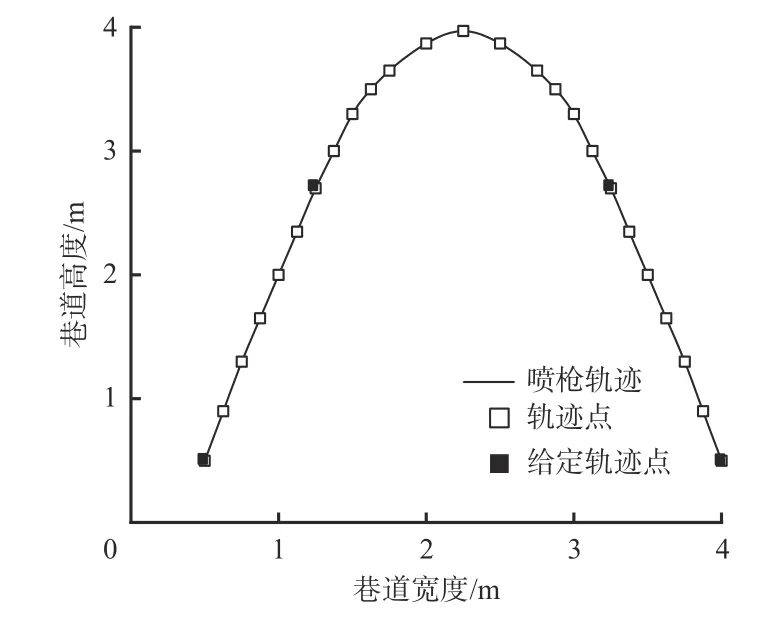
图10 工作臂运动轨迹Fig. 10 Working arm motion trajectory

将轨迹点（喷枪位置）数据代入式（18）对矩阵求逆解，得到各关节的关节位移和角度变化曲线，如图11所示。可看出工作臂的最大关节位移为-4.83 m，最大关节角为2.83 rad，未超过关节运动范围；各关节位移和角度曲线平滑，表明在喷浆过程中各关节运动连续、无突变。

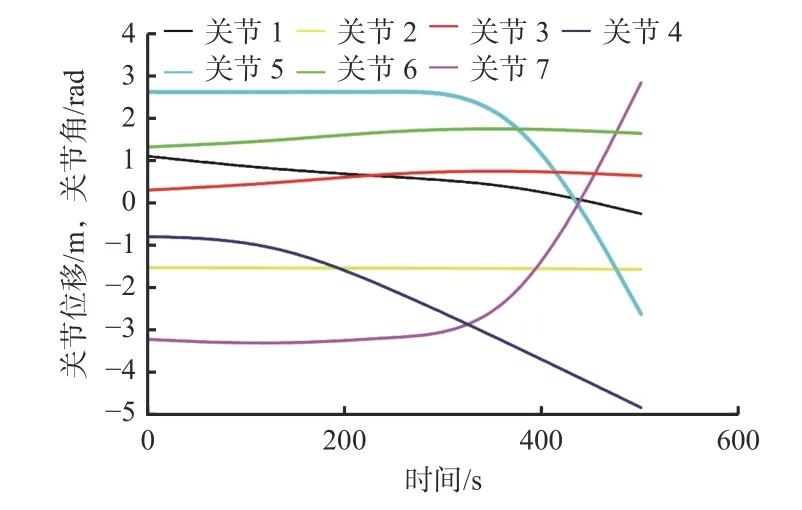
图11 工作臂关节变量变化曲线Fig. 11 The change curves of working arm joint variable

关节3 的速度和加速度曲线分别如图12 和图13所示。可看出关节3 的速度和加速度曲线均为连续、平滑的曲线，表明工作臂关节在喷浆过程中处于稳定运动状态。

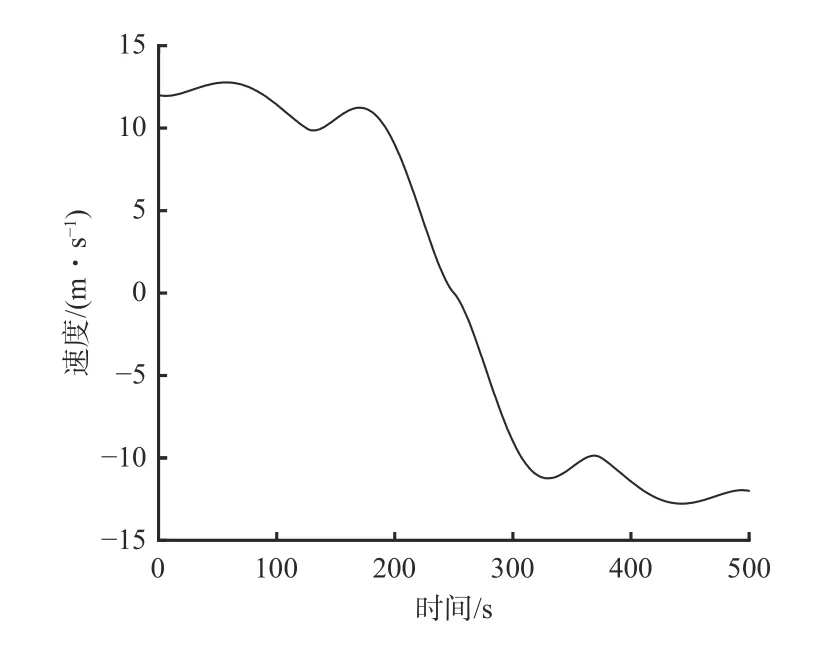
图12 关节3 速度曲线Fig. 12 Velocity curve of joint 3

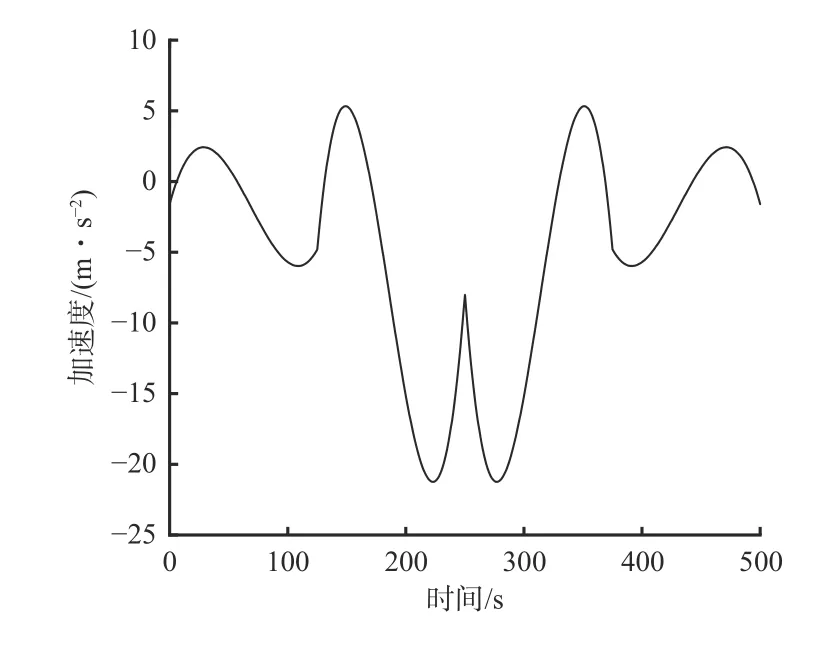
图13 关节3 加速度曲线Fig. 13 Acceleration curve of joint 3

4 结论

1） 对煤矿巷道进行截面划分，设计七自由度喷浆机器人在各截面间的移动轨迹和各截面上的工作臂运动轨迹，机器人移动轨迹规划和工作臂运动轨迹规划在每一个工作周期内交替进行，以保证喷浆机器人喷浆动作的连续性。

2） 根据机器人运动学模型，采用三次多项式插值法生成机器人移动轨迹，并利用MPC 算法对机器人移动轨迹进行跟踪控制，以实现机器人在巷道内准确、稳定移动。

3） 利用标准的D-H 参数法建立了机器人工作臂运动学模型，采用3-5-3 分段多项式插值法对机器人在各巷道截面的运动轨迹进行规划，得到了工作臂各关节的运动轨迹。

4） 仿真结果表明，MPC 算法可对机器人位置、方向角进行精确跟踪，且机器人移动速度稳定，实现了机器人在巷道内移动的准确性和稳定性；工作臂在喷浆过程中动作连续、喷浆轨迹稳定，满足巷道喷浆施工需求。