基于轴箱垂向振动加速度的地铁车轮失圆状态诊断方法

梁红琴，姜进南，陶功权，刘奇锋，卢纯，温泽峰，张楷，肖乾

(1.西南交通大学 机械工程学院，四川 成都，610031；2.华东交通大学 载运工具与装备教育部重点实验室，江西 南昌，330013；3.西南交通大学 牵引动力国家重点实验室，四川 成都，610031)

在地铁车辆长期的运营过程中，车轮容易出现非圆化磨耗[1]。多边形磨耗作为非圆化磨耗的一种特殊形式，会使得轮轨动态相互作用更加剧烈[2-3]，车辆轨道部件的振动也随之加剧，长时间的轮轨冲击也会加剧车辆轨道部件之间的磨损，严重时会导致轴箱裂纹，扣件断裂、轴承损坏等不良影响[4]。因此，及时识别多边形磨耗和判断其严重程度对车轮的运用维护具有重要的工程意义。

针对多边形磨耗的识别研究，学者们做了大量的相关研究。李忠继等[5]采用Hillbert-Huang变换(HHT)时频分析方法对比了扁疤冲击和车轮多边形磨耗引起的轴箱振动HHT谱特征的差异，发现正常车轮轴箱加速度HHT谱呈均匀分布，扁疤故障车轮呈纵向条带分布，车轮多边形化车轮呈横向条带状分布。李奕璠等[6]针对HHT模态混叠现象，基于形态学-能量原则算法提出了一种改进的HHT处理方法，可有效对正常车轮、多边形化车轮和擦伤车轮进行诊断。陈博等[7]提出一种基于改进的集合经验模态分解(MEEMD)和(采用遗传算法参数寻优的支持向量机分类器结合的车轮多边形磨耗识别方法)，其准确率能达95%。SONG等[8]提出了基于集合经验模态分解—魏格纳—威尔分布(EEMD-WVD)的多边形磨耗识别方法，对轴箱振动加速度进行时频分析，可以准确识别车轮多边形磨耗阶次。FANG等[9]提出了利用粒子群算法对变分模态分解(VMD)方法进行参数寻优，并对钢轨振动信号进行VMD分解，选取包络熵最小的前三阶IMF分量并求其峭度、能量、能量矩、Shannon熵、均方根值特征，以这些特征作为多核最小二乘支持向量机的输入，实现了对正常、二阶、三阶和四阶多边形磨耗的分类。

除利用时频特征进行多边形磨耗分类外，徐晓迪等[10]针对车辆动态响应，利用广义共振解调方法实现了车轮多边形磨耗的诊断。孙琦等[11]根据波长固定产生机理定位多边形磨耗阶数，结合轴箱垂向和横向加速度Welch谱估计其时域、频域特征，从而实现了多边形磨耗的检测。SUN等[12]提出了将多边形磨耗引起的时域振动信号转换为空间域振动信号和角度域的信号，通过查看空间域信号和角度域信号极值点的个数来判断多边形磨耗阶数。CHI等[13]等利用中国高铁定期检查和维护收集的大量数据，采用名义连续的合成少数过采样技术来增强不平衡和混合特征的维护数据集，自编码器用于提取特征，并结合支持向量机实现4个磨耗程度范围的多边形磨耗识别。ZENG等[14]基于车辆运行过程中相关因素设计了贝叶斯网络拓扑结构，并提出了基于贝叶斯网络的风险评估模型，将历史测量数据(包括部分缺失数据)即季节、车轮半径、列车类型等输入模型进行训练，可实现多边形磨耗轻度、中度、重度的分类。

上述文献提出的针对车轮多边形磨耗的识别都有一定效果，然而复杂的特征筛选和信号处理过程使得这类方法较为烦琐，并且限于个人信号处理经验，识别结果不稳定，在车轮多边形磨耗程度的识别上主要做了定性分析。卷积神经网络因其自适应提取特征能力强大而在机器视觉、故障诊断等领域得到广泛的应用。支持向量机具有良好的分类性能，同时在小样本、非线性问题上也有较好的表现。李大柱等[15]提出一种基于多尺度时频图与卷积神经网络(CNN)相结合的车轮故障智能诊断方法，该方法利用车轮所在轴箱垂向振动加速度来间接识别车轮服役状态。谢清林等[16]利用轴箱振动加速度构建一种基于一维卷积神经网络的地铁钢轨波磨智能识别方法，能有效、快速且稳定地对钢轨波磨进行智能识别与定位，在车辆复杂的运营条件及速度时变工况下仍然能保持较高的识别精度。卷积神经网络和支持向量机相结合的模型在轴承故障识别、民机升降舵故障诊断和利用无人机对车辆检测等领域得到了广泛应用[17-19]。因此，本文对比卷积神经网络、卷积神经网络结合支持向量机的模型及传统机器学习的深度置信网络和支持向量机在车轮多边形磨耗分类上的效果，并进一步对多边形车轮的磨耗程度进行了定量识别探索，提出基于代理模型和智能优化算法的车轮多边形磨耗波深识别方法。

1 车轮多边形磨耗识别流程

本文提出的车轮多边形磨耗识别流程框架如图1所示。图1(a)所示为车轮不圆顺输入，包括以数学模型模拟的不圆顺和现场测得的不圆顺；图1(b)所示为车轮多边形磨耗识别数据集的构建，将车轮不圆顺输入到考虑轮轨柔性的地铁车辆-轨道刚柔耦合动力学模型中，进而获取不同车轮状态下轴箱垂向加速度，并将其处理为分类识别数据集；图1(c)所示为车轮多边形磨耗分类识别，分别对比了一维卷积神经网络(1DCNN)、深度置信网络(DBN)、支持向量机(SVM)、以一维卷积神经网络全连接层特征为输入的支持向量机模型(1DCNN-SVM)模型在正常、低阶多边形化、高阶多边形化和随机非圆车轮等4种类别上的分类效果，从中遴选出适合车轮多边形磨耗分类的模型；图1(d)所示为车轮多边形磨耗波深识别预测，当分类识别结果为多边形磨耗时，通过频谱分析、包络谱分析等可以确定峰值频率，进而得到占主导阶次的多边形，再利用代理模型建立轴箱垂向加速度与车速和波深之间的映射关系，在进行波深识别时，以车速、轴箱垂向加速度为输入，通过智能优化算法在代理模型构建的响应面上求得波深。经过对比挑选出适合于车轮多边形磨耗波深定量识别的代理模型和智能优化算法。下文将进行详细的分析说明。

图1 车轮失圆状态识别流程Fig.1 Flow chart of wheel out-of-roundness state recognition

2 车轮多边形磨耗分类识别

2.1 车轮非圆化数学表达

车轮非圆化磨耗常采用含有1～N阶谐波的傅里叶级数形式的位移函数来表示[20]，即

式中：Ai为第i阶车轮不圆的幅值；φi为第i阶车轮不圆的相位；v为车辆运行速度；R为车轮平均半径；t为时间；N通常取40。

2.2 数据集构建

轴箱通过轴承直接与轮对连接，从轮对传递而来的振动并没有直接经过减振系统的作用，轴箱振动加速度能较为直接地反映轮轨冲击振动的特征。因此，本文采用轴箱垂向加速度信号来构建数据集。

实际情况下，车轮多边形化状态时的轴箱加速度信号样本有限且故障类型不够丰富，地铁车轮多边形磨耗容易激发轮轨系统P2共振，且在对车轮多边形磨耗的中高频激励进行动力学分析时，将轮轨柔性化处理能够切实反映轮轨系统固有模态共振等现象[21-22]。因此，本文基于某B型地铁车辆和轨道参数建立地铁车辆-轨道刚柔耦合动力学模型，该模型由1个车体、2个构架、4个轮对、8个轴箱构成，其中轮对考虑柔性，其他部件为刚体。车体、构架均考虑伸缩、横摆、浮沉、侧滚、点头和摇头6个自由度；轴箱只考虑点头自由度。一系垂向减振器、二系垂向减振器、二系横向减振器及横向止挡等均使用非线性函数来表征。车轮踏面采用S1002型面，钢轨型面采用CN60，并将钢轨考虑为离散连续支撑的Timoshenko梁。钢轨和轮对的有限元模型及子结构分析均在有限元软件ANSYS中进行。通过动力学软件SIMPACK的FE-MBS和Nonlinear Flextrack模块可实现轮对和轨道的柔性化。车辆和轨道模型的参数和刚柔耦合建模流程可参见文献[2]和[22]，同时，该模型在之前的研究中已利用实测数据进行过验证，不再赘述。

数据集由不同车轮磨耗情况下的轴箱垂向加速度响应构成，包含正常车轮、低阶多边形化车轮、高阶多边形化(通常大于9阶称为高阶多边形)车轮、随机非圆化车轮4个类别。正常车轮是半径为0.42 m的理想车轮，因为地铁车辆常出现低阶多边形磨耗如5～8阶[23]，高阶多边形磨耗如12～14阶[24]、11～16阶[25]，为考虑故障样本的均衡性，故本文低阶多边形化车轮考虑5～8阶，径跳为0.1～0.5 mm；高阶多边形化车轮考虑12～15阶，径跳为0.1～0.5 mm；随机非圆化车轮径跳为0.1～0.5 mm。考虑到实测车轮不圆顺的类别及丰富性，车轮不圆顺的输入采用实测的车轮不圆顺和利用式(1)生成的车轮不圆顺，仿真考虑美国五级轨道谱，采样频率为5 000 Hz，仿真时间为1.4 s，车辆运行速度为75 km/h，共仿真获取960条轴箱垂向加速度数据，各类别车轮典型非圆化形式及其轴箱垂向加速度如图2所示。为了扩充数据集，对仿真获取的每条轴箱垂向加速度数据取其中5 120个数据点进行滑窗处理，考虑到样本长度设置为2的幂函数可以使数据集大小更加灵活，同时考虑到车轮滚动3圈的采样点数为1 900个，因此，将每条样本的数据长度设置为2 048，滑窗步长设置为1 024。最终通过滑窗处理，得到了3 840条样本数据，数据集构成如表1所示。

表1 数据集构成Table 1 Composition of dataset

图2 车轮非圆化形式及轴箱垂向加速度Fig.2 Form of wheel out-of-roundness and vertical acceleration of axle box

2.3 车轮失圆状态分类模型构建

为了从常用的分类算法中挑选出适合于车轮失圆状态分类识别的算法，构建1DCNN、DBN、SVM及CNN-SVM模型。除了SVM外，其他算法都无需人为对信号进行特征提取。下面简单介绍DBN算法，同时以1DCNN-SVM为例详细说明分类模型构建过程。

深度置信网络(DBN)是一个概率生成模型，由多层受限波尔兹曼机(RBM)堆叠而成，其网络结构被限制为2层：可视层和隐层。其中，可视层包含输入数据的特征，而隐层则由多个节点组成，用于捕捉可视层中的高阶特征。在训练过程中，每个RBM都通过最大似然估计方法进行训练。具体地，上一个RBM的隐层即为下一个RBM的显层，上一个RBM的输出即为下一个RBM的输入。这种逐层训练的方法可以有效地解决深度神经网络中梯度消失和梯度爆炸等问题，同时也使DBN可以从数据中自动学习特征，最后，DBN通常通过在最后一层添加一个分类器来进行分类任务。

用于分类识别的数据集由轴箱垂向振动加速度构成。针对一维时域序列信号，为更好地获取分类信息，采用1DCNN来提取输入样本的特征，SVM作为分类器。图3所示为构建的1DCNNSVM模型，其中卷积神经网络部分包含输入层，3层卷积池化层。第一层卷积层卷积核个数较多是为了获取信号不同角度的特征，3层卷积层卷积核的长×宽都为1像素×3像素，激活函数采用ReLU激活函数，能有效避免梯度消失现象，池化函数选择最大池化，分类层采用SVM作为分类器，完整的1DCNN网络结构参数如表2所示。

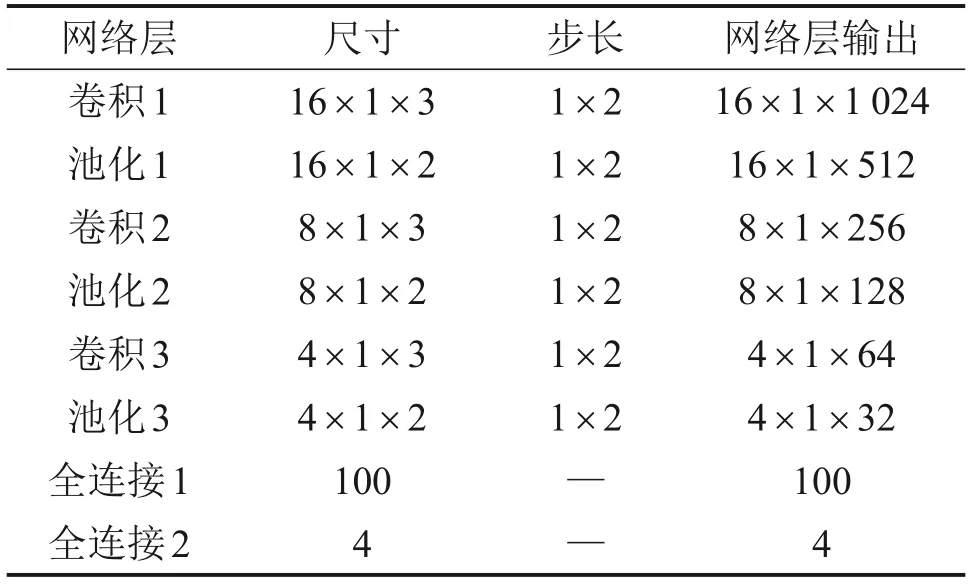
表2 1DCNN模型参数Table 2 Parameters of 1DCNN model像素

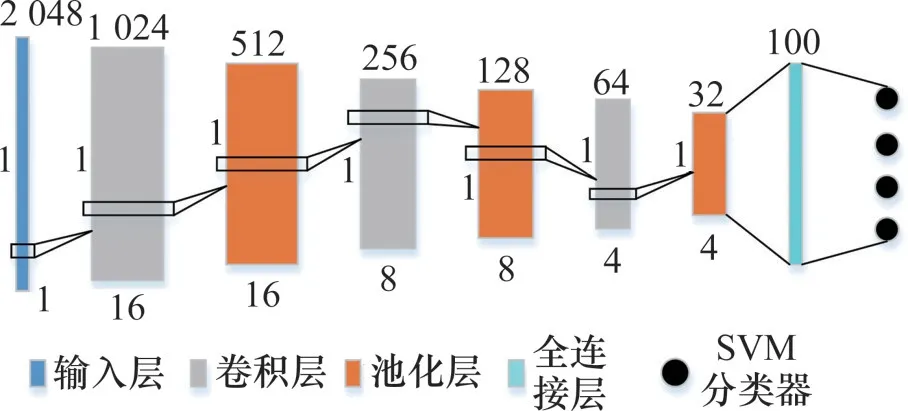
图3 1DCNN-SVM模型示意图Fig.3 Schematic diagram of 1DCNN-SVM model

为了加快模型收敛，在全连接层引入Dropout层，并设置Dropout=0.5，优化器选取Adam优化器，学习率为0.001，损失函数为交叉熵函数，批处理样本数量为128个。1DCNN网络模型训练好后，提取第一层全连接层的输出特征作为SVM的输入特征向量，再训练SVM模型，最后得出分类结果。在用SVM进行多分类任务时，采用“一对一法”，即对于m类样本，每2类样本构造1个分类器，共构造m(m-1)/2个子分类器。在预测样本所属类别时，每个子分类器都对其进行判断并为对应的类别投票，最后决策时以票数多的类别作为预测样本的类别。

为使对比结果不失一般性，1DCNN分类模型与1DCNN-SVM模型中卷积神经网络部分结构和参数一致；DBN分类模型则使用3个RBM(受限玻尔兹曼机)层，每一层的神经元个数与前述1DCNN每一层输出数据量相同，3层神经元个数分别为8 192、1 024和128；支持向量机分类模型则以信号的均值、方差、标准差、均方根、偏度、峭度、脉冲因子、峰值因子、波形因子、平均频率、重心频率、均方频率、频率方差等13个时域和频域特征作为输入，并使用遗传算法(GA)对支持向量机参数进行优化。

2.4 识别结果对比分析

为提高模型的泛化学习能力，同时避免模型欠拟合等问题，针对3 840个数据集样本，通过多次实验最终确定将数据集以7:3比例划分为训练集和测试集，输入到CNN-SVM模型中训练。迭代次数为150次；支持向量机的惩罚因子通过K折交叉验证确定为0.75。图4所示为1DCNN网络第一层全连接层的特征可视化结果，因未对第一层全连接层降维后的结果进行归一化处理，它的每一行代表一个样本在二维空间中的坐标。图中横纵坐标无物理含义，坐标距离只反映样本之间的相似性，因此，可以看出1DCNN训练后第一层全连接层的聚类效果较好，数据很明显被分为4类，只有少部分样本误分。

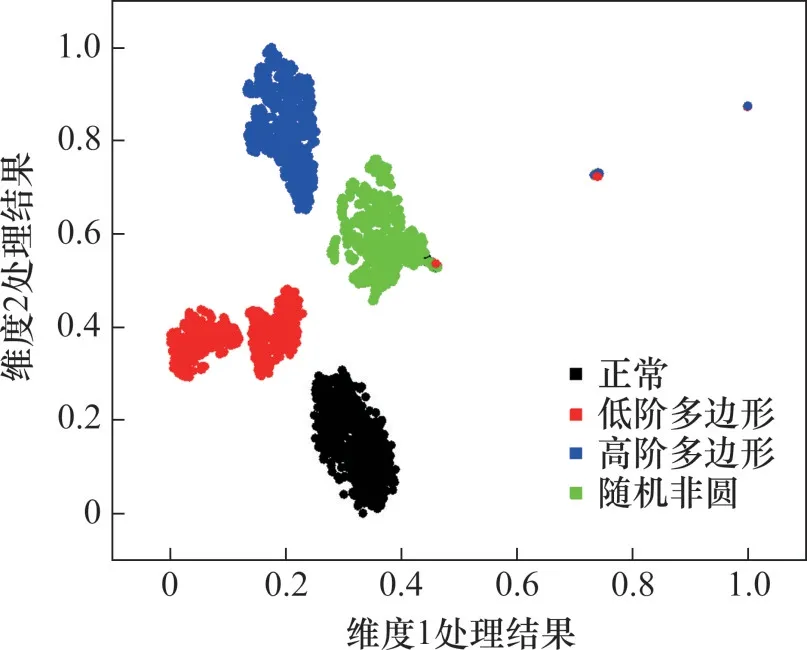
图4 1DCNN全连接层特征可视化Fig.4 Visualization of 1DCNN fully connected layer feature

图5所示为1DCNN-SVM分类的混淆矩阵，从图5可以看出：有少量低阶多边形被误分，1DCNN-SVM的分类准确率为99.82%。通过网络全连接层的特征可视化和混淆矩阵可以看出被误分的样本中主要是低阶多边形类别误分为随机非圆类别。通过分析低阶多边形不圆顺和随机非圆不圆顺的阶次图发现，低阶多边形不圆顺中部分低阶和高阶成分与随机不圆中阶次成分较接近，因此，导致少量低阶多边形磨耗样本聚类至随机非圆一类。

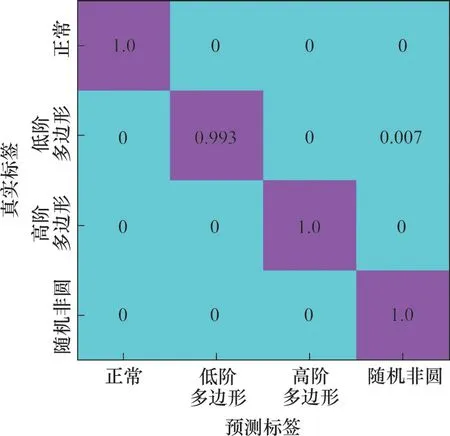
图5 1DCNN-SVM混淆矩阵Fig.5 Confusion matrix of 1DCNN-SVM

1DCNN-SVM与1DCNN、DBN、支持向量机的识别结果如图6所示。为了验证算法的泛化性能，对测试集加入了信噪比为3 dB的高斯白噪声。从图6可以看出：在测试集不加噪和加3 dB信噪比噪声的情况下，1DCNN-SVM算法精度分别为99.82%和81.94%，识别率在几种算法中最高，其次1DCNN虽然在测试集不加噪的情况下取得了很高的识别精度，但在加噪情况下，算法的泛化性比1DCNN-SVM的差。DBN则在2种情况下都未能取得较高的识别精度，相比1DCNN其学习数据特征能力明显不足。SVM方法在不加噪情况下获得了较好的识别效果，但高斯白噪声的加入对数据的极值点分布、时域和频域特征特性等影响较大，从而影响信号的时频特征，导致在测试集加噪情况下，识别效果不尽人意。因此，1DCNNSVM模型更适合车轮多边形磨耗分类并且具有较好的泛化能力。

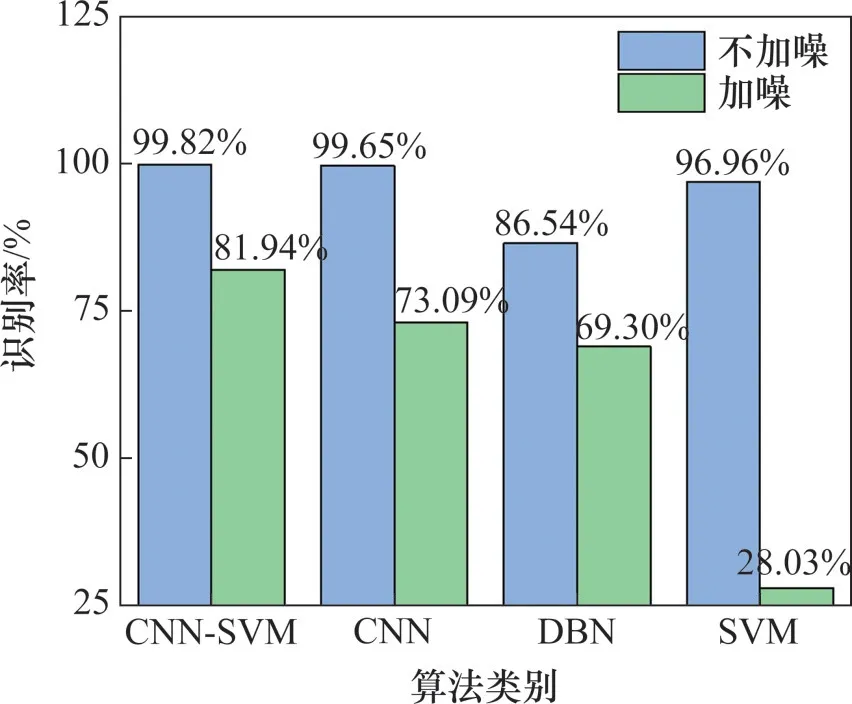
图6 不同算法的故障识别率对比Fig.6 Comparisons of fault recognition rates among different algorithms

为了进一步验证1DCNN-SVM模型的泛化和强化学习能力，在训练集中随机选取少量样本加入不同信噪比的高斯白噪声，训练集具体添加噪声情况如表3所示。

表3 含噪声的训练集Table 3 Noise-containing training set

按表3往训练集添加不同信噪比后，经过一定次数的迭代训练，其测试结果如图7所示。由图7可知：训练集少量样本加入噪声后，1DCNN-SVM模型对加噪测试集的识别率得到了较大的提高，在信噪比为3 dB的加噪测试集最高有97.48%的准确率，在低信噪比情况下识别准确率也在90%以上，说明该模型可以从少量加噪的训练集中学习到含噪声的数据特征，在复杂的数据情况下，可不断学习和优化。

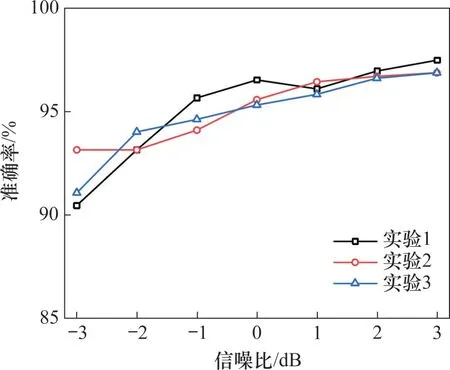
图7 不同情况下加噪测试集的识别结果Fig.7 Recognition results of noisy test set at different conditions

为了体现1DCNN-SVM模型在实际条件下的识别情况，选取一段如图8所示的现场试验测得的轴箱垂向加速度，通过现场测试，该多边形化车轮的主要阶次为6～8阶。为保持一致，按照仿真数据集单个样本长度对实测数据进行划分，共得到28条样本，输入到上述通过仿真数据训练得到的1DCNN-SVM模型，所有测试样本均被识别为低阶多边形磨耗，即5～8阶多边形，识别结果与实际测试结果一致，再对信号进行频谱分析、包络谱分析等即可根据峰值频率确定占主导的多边形磨耗阶数。因此本文所构建的1DCNN-SVM模型识别精度高且可用于实际工程中的多边形磨耗分类识别。

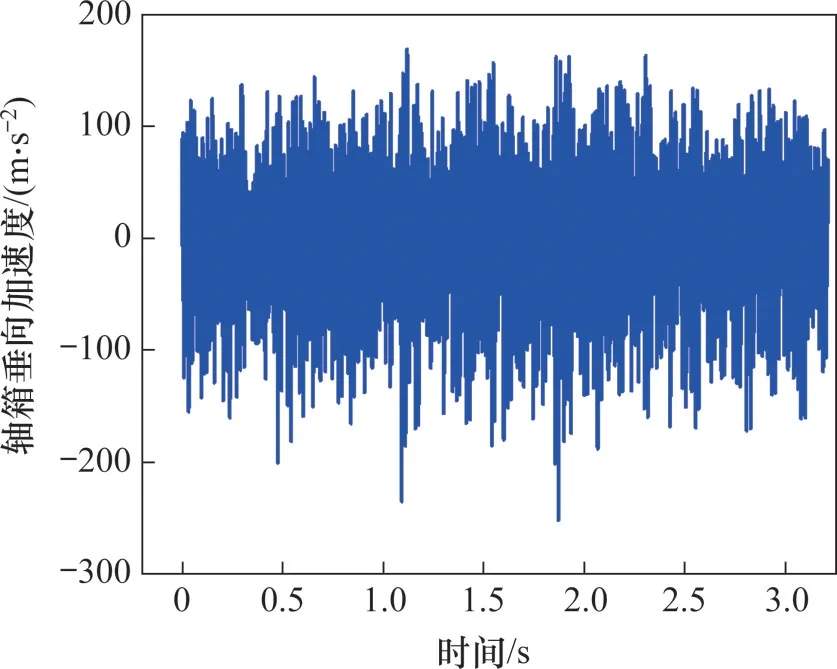
图8 实测多边形化车轮条件下的轴箱垂向加速度Fig.8 Measured vertical acceleration of axle box with condition of polygonal wheel

3 车轮多边形磨耗波深识别

在多边形磨耗波深较大时，车辆性能指标可能超过安全限值，因此，在识别出多边形磨耗阶数后，应对车轮多边形磨耗波深进行估计。本文利用代理模型建立多边形磨耗波深、车速和轴箱垂向加速度均方根(RMS)之间的映射关系，以此代替计算复杂耗时的仿真模型；基于已知的车速和轴箱垂向加速度均方根(RMS)，利用智能优化算法在代理模型响应面上逆向求解多边形磨耗波深。代理模型选择常用的克里金模型(KSM)、多项式响应面(RSM)、径向基函数(RBF)，智能寻优算法选择常用的粒子群算法(PSO)、模拟退火算法(SA)、遗传算法(GA)，并从中遴选出适合多边形磨耗波深识别的代理模型和优化算法。下面以克里金模型为例说明代理模型的构建过程。

3.1 代理模型构建

构建代理模型需要先确定映射的输入与输出。在已知车轮多边形磨耗阶数后，将多边形磨耗简化为谐波磨耗，以车速和波深作为输入，以轴箱垂向加速度为输出构建代理模型，考虑到地铁车辆复杂的实际运营环境以及车辆轨道系统共同作用等非线性因素，轴箱垂向加速度信号易受噪声影响，产生随机干扰[26]，因此，轴箱垂向加速度采用其均方根来表示(符号为eRMS)，以保证鲁棒性。为了保证样本点均匀的充满设计空间，采用均匀实验设计方法，以7阶车轮多边形磨耗为例，利用建立的地铁车辆-轨道耦合动力学模型对11种车速(30、35、…、80 km/h)、10种波深(0.05、0.10、…、0.50 mm)进行仿真计算，仿真时轨道激励为美国五级谱，仿真计算得到的样本情况如表4所示。KSM的主要思想是基于无偏估计和均方误差最小假设，把未知函数看作某个随机过程，利用预测点附近的已知样本点信息加权来获得预测点的响应值。用克里金模型来构建代理模型，相关函数选择常用的高斯模型，因为该模型能够得到一个相对平滑且无限可微的表面，KSM模型回归部分设为常数1。同样地，对于RSM和RBF方法，按照表4的样本建立代理模型，通过试算，RSM使用二元二次多项式，RBF方法采用多元二次函数。

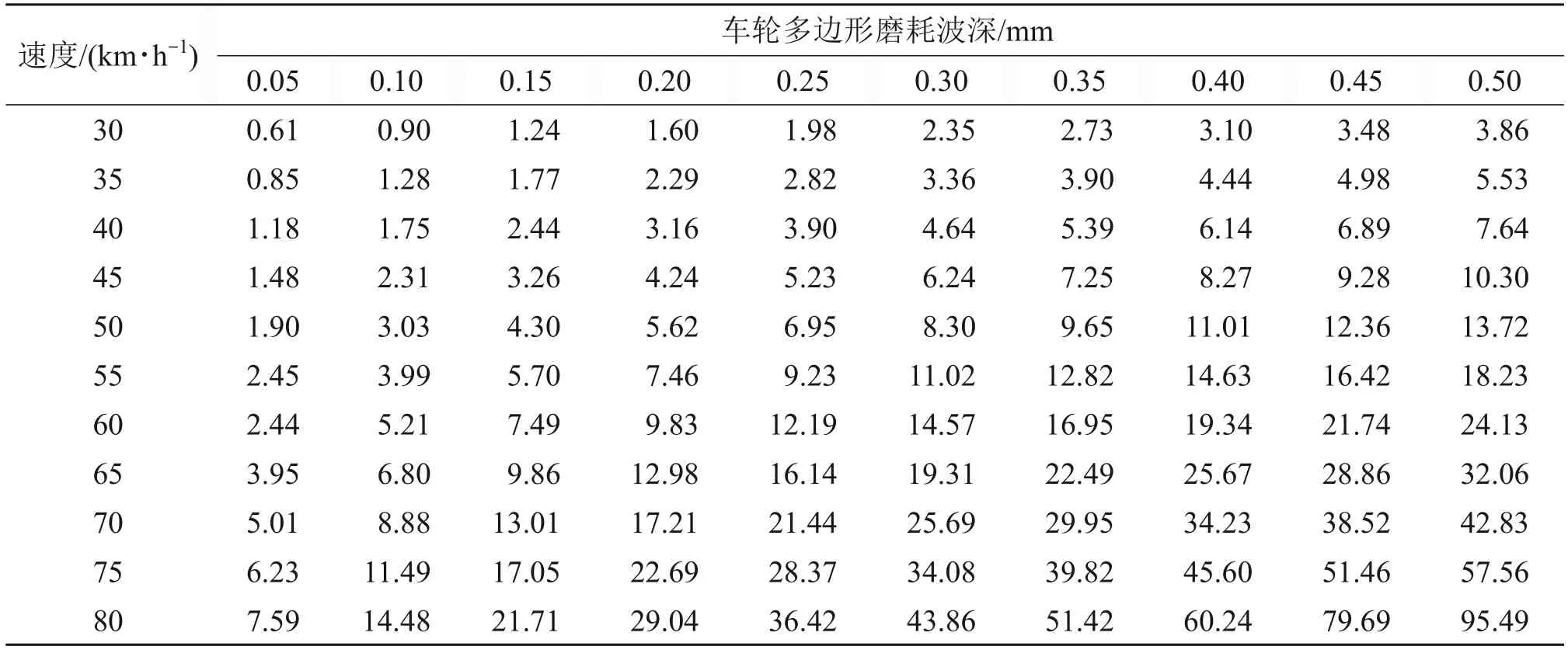
表4 7阶多边形磨耗条件下轴箱垂向加速度均方根Table 4 Root mean square of vertical acceleration of axle box with condition of 7th-order polygonal wearm/s2

3.2 代理模型对比

3种代理模型构建的响应面如图9所示。从图9可以看出：KSM构建的响应面较为光滑，样本点均在响应面上，拟合程度较好；虽然RSM响应面较为光滑，但有很大一部分样本点并不在曲面上，且有些点偏离响应面较远，故其预测精度较低，同时也从侧面说明了车速、波深和轴箱加速度之间的非线性关系较强，RSM模型无法很好地构建三者之间的映射关系；RBF其响应面局部是光滑的，从整体看，响应面表现出波浪状的变化，而设计样本点则在2个波的交界处上，未知响应点则在波峰与波谷曲面上。

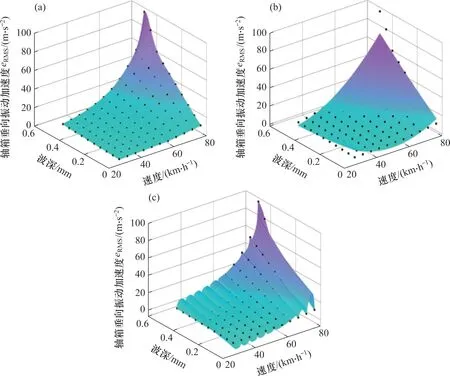
图9 3种代理模型构建的响应面Fig.9 Response surfaces constructed by three surrogate models

代理模型的精度对波深识别具有重要影响。为验证代理模型精度，在样本空间内随机挑选3种车速38、53和72 km/h，每种车速下随机选取3种波深，得到用于验证代理模型精度的9种工况，如表5所示。

表5 KSM模型精度验证Table 5 Accuracy verification of KSM model

按照表5的验证工况，代入动力学仿真模型中计算，得到相应的轴箱加速度eRMS及相对误差绝对值，与代理模型预测结果进行比较，同时表5给出了KSM的预测精度，最大相对误差为1.23%，最小相对误差为0.03%，平均相对误差为0.49%。3种代理模型精度对比结果如图10所示，从图10可以看出：RSM模型的相对误差为4.11%～44.31%，平均相对误差为17.84%，预测精度较差，且预测精度较为不稳定；RBF模型预测的最小相对误差为2.70%～141.84%，平均相对误差也达到了32.30%，虽然最小相对误差较RSM模型小，但其最大和平均相对误差仍然较高，预测稳定性最差，从RBF的响应曲面来看，波浪状的曲面有些部分严重脱离样本点所在的整体位置。因此，KSM模型具有较好的预测精度和预测稳定性，可以用于替换原有动力学模型做相关计算。

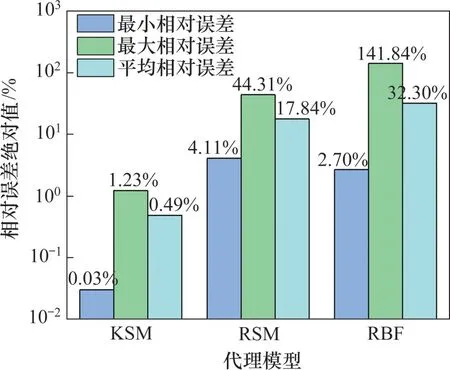
图10 3种代理模型精度对比Fig.10 Accuracy comparisons of three surrogate models

3.3 波深逆向寻优

代理模型的构建能一定程度上代替复杂耗时的仿真模型，在响应曲面构建好后，需结合智能优化算法进行波深的求解预测。利用智能优化算法逆向寻优的目标函数如下[27]：

式中：Hj为加权参数(x)为样本点在KSM中对应预测值的第i个分量；yi为实际的响应分量。

代理模型选择效果较好的KSM模型，将车辆实际运行速度与测得的轴箱垂向振动加速度eRMS作为一组输入代入KSM响应面，采用智能优化算法按式(2)进行寻优，找出当前车速和轴箱加速度eRMS所对应的波深。

3.4 智能优化算法对比

在PSO算法求解问题的过程中，粒子的优劣用适应度表示，而粒子的位置和速度也在求解问题的过程中不断发生变化，粒子之间的信息交流使得粒子向着最优的方向靠近。随机选择9种验证工况如表6所示，其中PSO预测的最大相对误差为1.33%，最小相对误差仅为0.06%，平均相对误差0.50%。PSO、SA和GA在表6工况下进行预测的结果对比如图11所示，从整体看三者寻优结果相对误差相差不大，其中SA最小相对误差为0.05%，为三者中最小，而GA最大相对误差为1.39%，为三者中最大，PSO、SA和GA三者的平均相对误差分别为0.50%、0.54%和0.56%，PSO算法平均相对误差最小。3种算法的精度都满足本文的寻优要求，考虑到工程实际应用，优化算法还要考虑到可操作性、可实现性及算法耗时情况。因此，下面针对算法的时效性进行对比。

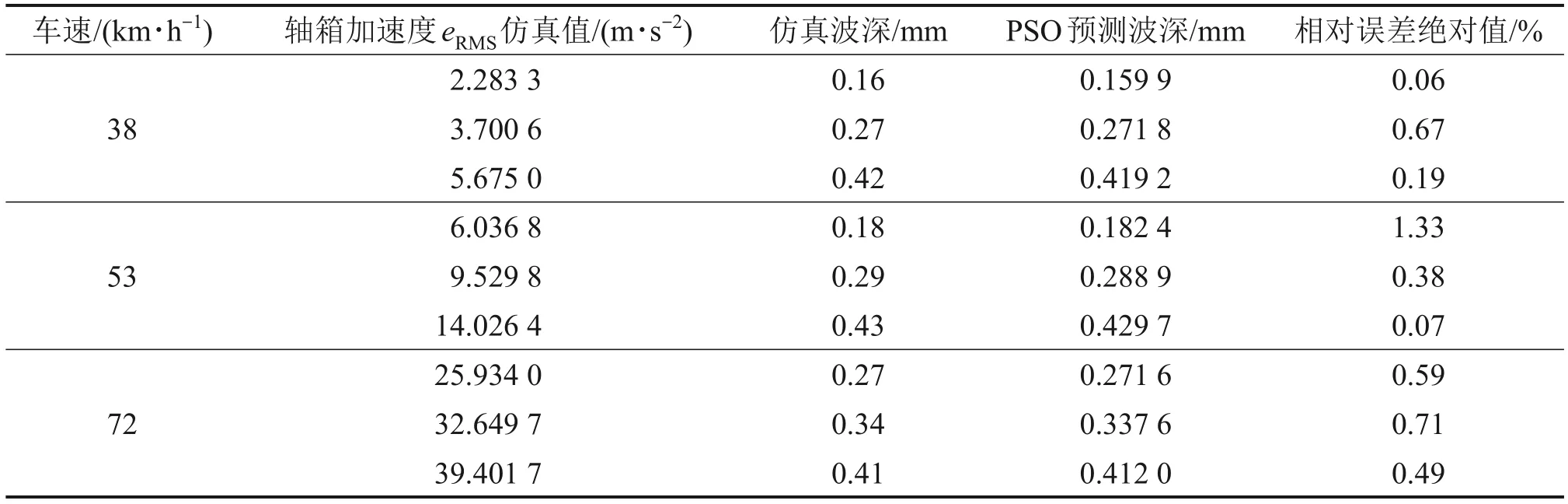
表6 PSO预测精度Table 6 Prediction accuracy of PSO

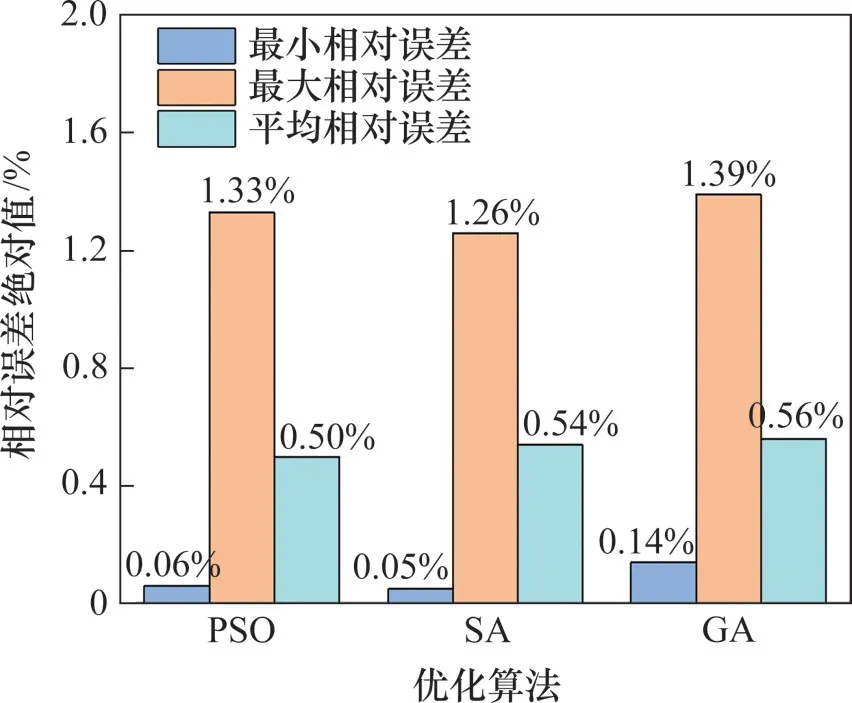
图11 3种优化算法相对误差对比Fig.11 Relative error comparisons of three optimization algorithms

在表6所示的9种验证工况下，分别统计3种算法求解耗时，其统计结果如图12所示。由图12可知：SA算法耗时最多，平均耗时9.83 s，PSO算法和GA算法耗时相对较少，分别为0.11 s和0.26 s。SA平均耗时是PSO的89.36倍，GA平均耗时为PSO的2.36倍，因此，在面对大量的实际数据时，PSO算法的处理效率能为波深预测节省大量时间。在预测精度方面，PSO的平均相对误差略低于SA和GA，算法耗时方面PSO也体现出了明显的优势，并且操作简单、参数设定少[28]。综合来看，PSO是用于车轮多边形磨耗在线监测的合理选择。

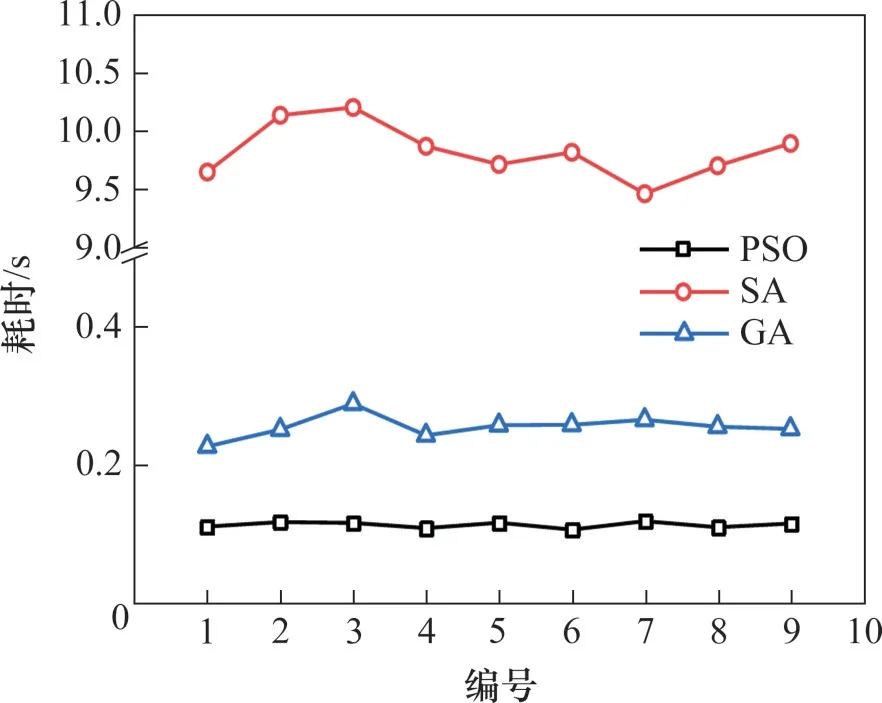
图12 3种优化算法耗时对比Fig.12 Time-consuming comparisons of three optimization algorithms

因此，通过构建KSM-PSO模型能够实现替代复杂的仿真模型，并且能以较高的精度实现波深的预测，可根据实际现场的车速与轴箱加速度eRMS实现对波深的估计。

4 结论

1) 将SVM分类器代替CNN的Softmax分类器，构建1DCNN-SVM多边形磨耗分类模型，识别率达到99.82%，在实测数据的识别中也达到了较好的分类效果。与常用的1DCNN、DBN、SVM算法相比，1DCNN-SVM的泛化性能和强化学习能力更好。

2) 针对多边形磨耗波深，结合代理模型和智能优化算法对波深预测做了探索。在3种代理模型中，KSM的预测效果和稳定性最好，其平均相对误差不超过0.50%。在多边形磨耗波深逆向寻优过程中，3种寻优算法的精度相近，但SA和GA平均耗时分别为PSO的89.36倍和2.36倍。

3) 针对车轮多边形磨耗的分类识别问题，基于卷积神经网络的分类识别方法在特征提取、泛化性能、强学习能力上更好。在多边形磨耗波深的识别方面，KSM和PSO算法在预测稳定性和耗时方面更具优势。建议在车轮多边形磨耗分类识别时采用1DCNN-SVM模型，而在车轮多边形磨耗波深定量识别时建议采用KSM-PSO模型。