小口径CFRP-方截面钢管混凝土受弯性能研究

2024-03-01戴雨辰陈铁林王风

中南大学学报（自然科学版） 2024年1期

戴雨辰，陈铁林，王风

(1.北京交通大学隧道与地下工程教育部工程研究中心，北京，100044；2.北京交通大学土木建筑工程学院，北京，100044；3.国能朔黄铁路发展有限责任公司原平分公司，山西忻州，034100)

随着中国经济发展水平不断提高，城市化进程加快，城市规模不断扩大，人口不断增加，城市交通也变得越来越重要。作为相对比较低碳而又高效的出行方式，地铁出行一直是人们的首选。但对于软土地层区域的地铁隧道，地质条件不良、人口密度增大以及频繁的建筑活动等导致隧道结构发生变形、开裂甚至破坏，这严重影响了地铁设施正常运营[1-3]。

近年来，钢管混凝土与碳纤维复合材料(CFRP)构件相结合的结构应用越来越广泛[4-6]。为了减小隧道内部的不均匀沉降带来的危害，本文采用CFRP-钢管混凝土结构对地铁隧道内部进行加固。钢管混凝土是指在钢管中填充混凝土且钢管及其核心混凝土能够共同承受外荷载作用的结构构件，具有承载力高、延性好、施工方便等特点[7-11]。近年来，有关研究以CFRP外缠钢管凝土柱的轴压性能、抗震性能、侧向抗冲击性能为主[12-16]，研究对象则多为短柱和柱梁节点。研究表明，在钢管混凝土CFRP结构中，增加CFRP的厚度既可以提高构件整体的刚度和强度，减少用钢量，还可以避免钢管腐蚀；王庆利等[17-19]发现提高钢管的含钢率可以增强构件的承载能力，使用CFRP可以延缓构件的屈曲；王宇航等[20]研究了CFRP环向约束钢管混凝土柱在多种荷载作用下的力学性能，发现在压弯扭荷载作用下，环向CFRP布能够有效提高试件的延性以及耗能能力，但对试件承载力的提升不明显，增加环向CFRP层数可以有效抑制钢管的弯曲。FERDOUS等[21]提出采用四点弯曲试验来验证构件的抗弯刚度。实验表明，相比于增加混凝土量(仅提高2.6%)，增加FRP厚度(3～10 mm)可以使抗弯刚度增加1倍。当需要提高构件的抗弯刚度时，增加管壁厚度比填充混凝土更有效；KEYKHA等[22]采用三维建模和非线性静力分析方法，研究了碳纤维布加固对竖向曲线钢梁性能的影响。

传统的钢管混凝土结构多用作短柱、长柱等受压结构，且横截面边长一般为500～1 200 mm。由于地铁隧道净宽限制，不允许占用过多空间，故采用小尺寸构件更合理。目前，人们对小口径CFRP-方截面钢管混凝土的研究较少。针对软土地区地铁隧道内部的不均匀沉降带来的危害，本文提出采用新型的小口径CFRP-方截面钢管混凝土结构作为支护结构对隧道内部进行环形加固，从而减少裂缝的数量和隧道结构的变形。标准地铁隧道断面宽度为6 000 mm左右，本文采用的小口径试件实际横截面边长不超过45 mm，在隧道内沿隧道内壁环形布置。在综合考虑隧道尺寸和试件尺寸的关系后，将试件受力模型简化为梁受弯模型进行试验和数值模拟计算。对CFRP-钢管混凝土抗弯性能进行试验研究。分别对钢管、水泥和CFRP布3种材料不同组合方式所得结果进行对比，探讨其破坏形态、荷载-位移曲线特点以及CFRP布对抗弯承载力和抗弯刚度的影响，并将试验结果与ABAQUS软件所得荷载-位移曲线和破坏模式进行对比。

1 试验概况

1.1 试验设计

本次试验设计12组试件。试件的长度L为500 mm，试件净跨l为490 mm，方钢管外径分别为30、32和35 mm(分别对应试件A、B和C)，钢管的壁厚为2 mm。灌注的水泥净浆立方体试块抗压强度为40 MPa。单层CFRP布厚度为0.167 mm，试验厚度为1 mm。分别对12组试件进行4组试验，其中包括钢管组、钢管+水泥组、钢管+CFRP布组以及钢管+水泥+CFRP布组。具体试件参数见表1。

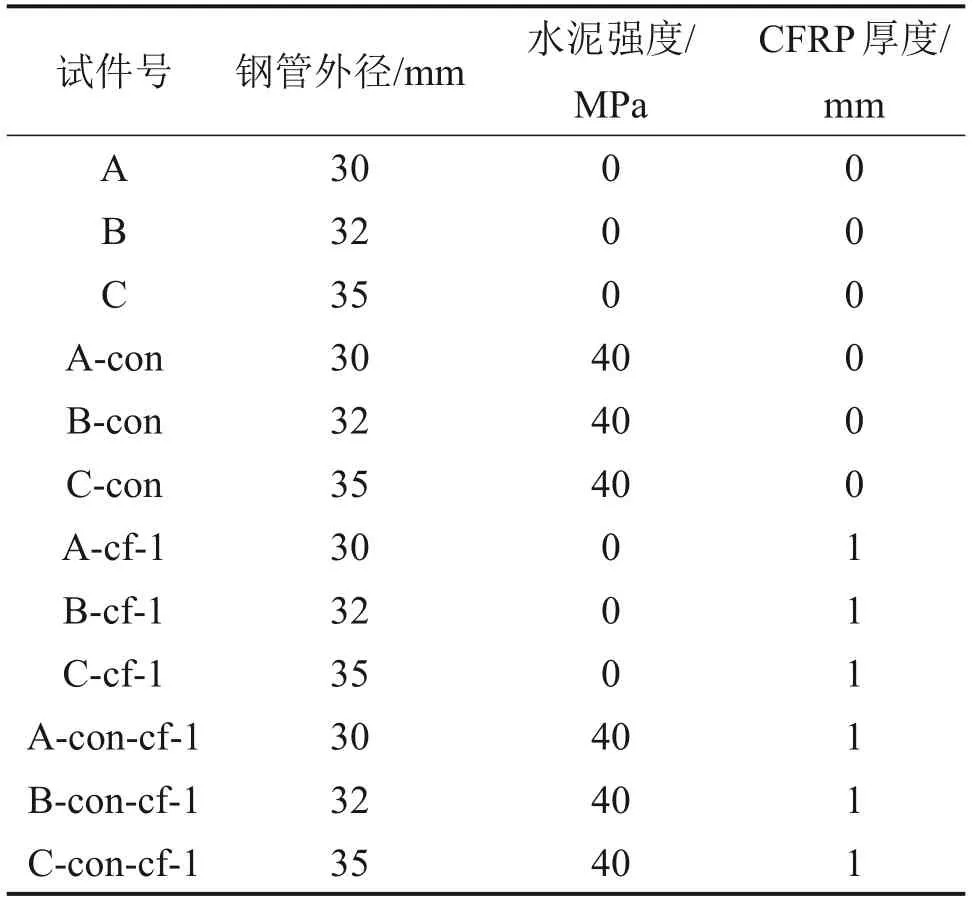
表1 试件参数Table 1 Parameters of specimens

所有试件的填充物均采用养护7 d的P.O 42.5的水泥净浆，按标准实验程序测得试块抗压强度均值为40 MPa。

钢管为经过圆化处理后的方钢管。在拉伸试验前，将钢管沿纵向剖开，取3个厚度为2 mm的标准试件进行拉伸试验。由标准拉伸试验测得的屈服强度和极限强度如表2所示。

表2 钢管材性Table 2 Properties of the steel tube

CFRP为300 g一级的单项碳纤维布，纤维沿纵向分布。由于碳纤维布厚度为0.167 mm，在粘贴时，需要粘贴6层单项碳纤维布以满足试验厚度要求。CFRP材性见表3。

表3 CFRP材性Table 3 Properties of CFRP

试件的截面和应变片分布示意图如图1所示。

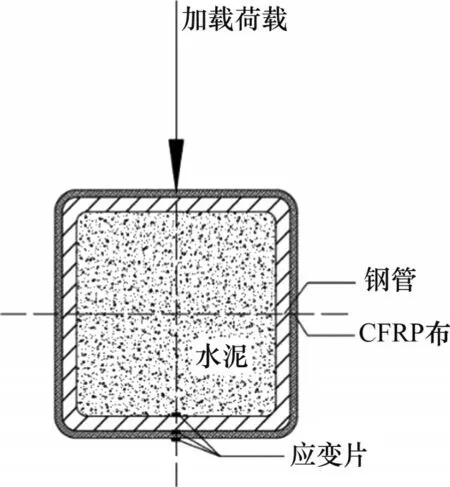
图1 截面与应变片分布示意图Fig.1 Diagram of the cross-section and distribution of the strain gauges

1.2 加载装置

使用WAW-100万能试验机进行三点弯曲试验的加载。加载装置如图2所示。试验加载装置由试验加载底座、侧向支架、压头和负荷传感器以及所连接的计算机组成。通过压头以及侧向支架固定试件，由负荷传感器将试验所得的荷载与位移传送到计算机中。试件两端简支，跨中加载。以1 kN/s的加载速度进行加载。当试件加载到荷载大幅度下降或试件出现脆性破坏或试件跨中位移达到50 mm时，停止加载。

图2 加载装置Fig.2 Loading equipment

1.3 试件制备

1) 钢管内部空间狭小，故首先在应变片一侧粘贴双面胶，用直尺将其送到对应位置后轻轻拍打，使应变片固定在钢管内部。

2) 将钢管一侧用布缠住，将水泥与水混合，每1 kg水泥加400 mL水。充分搅拌后，使用小铁铲将水泥灌注到钢管内部；在灌注过程中，分4次振捣，每次振捣至不再有小气泡出现时，再继续振捣30下。灌注水泥后，将试件静置养护7 d。

3) 将钢管外部擦拭干净，并用锉刀对其进行打磨，然后将应变片粘贴至钢管跨中底部(与钢管内部应变片处于同侧)。

4) 粘贴完应变片与钢管后，在钢管外部缠绕对应厚度的CFRP布。使用碳纤维浸渍AB胶，将其按比例混合后充分搅拌均匀，待浸渍胶混合均匀后在CFRP布上涂抹浸渍胶。在粘贴CFRP布时，需要边缠布边刷胶，不断用刮板沿纤维方向挤压以排除中间气泡的影响，目的是使碳纤维布粘贴得更为均匀。

5) 待浸渍胶凝固后，在试件跨中底部粘贴应变片。

2 试验现象及结果分析

2.1 试验破坏现象

试验分为单钢管试验组(I组)、钢管+水泥试验组(II组)、钢管+CFRP布试验组(III组)、钢管+水泥+CFRP布试验组(IV组)；在三点弯曲试验中，第I组和III组以试件跨中上方压溃以及侧面鼓曲为破坏标志，试件破坏现象见图3(a)和图3(c)。第II组试验破坏现象为试件跨中上方轻微压溃并伴随跨中侧向微鼓曲，破坏现象见图3(b)。第IV组试件跨中上方CFRP布被压断，并产生沿横向的断裂；跨中下侧CFRP布被拉断，具体破坏现象见图3(d)。

图3 试件破坏现象Fig.3 Destruction phenomena of specimens

2.2 荷载-位移曲线分析

图4所示为实测的三点弯曲试验中的荷载-位移曲线。从图4可以观察到，随着钢管的外径增加，同组构件承载力增大，二者呈正相关；试件的荷载-位移曲线变化趋势与截面类型和构件的材料组成有关，可以分为以下几类。

1) 第1类，荷载-位移曲线分为弹性阶段、弹塑性上升阶段以及下降段。试件在弹性阶段的荷载-位移曲线可用正比例函数表示。荷载先迅速上升，在进入弹塑性阶段后荷载上升速率大幅度减小，无明显峰值点，经过峰值点后，曲线呈下降阶段。试件直径越大，下降段速率变化越快。

2) 第2类，荷载-位移曲线分为弹性阶段、弹塑性上升阶段以及强化平稳阶段。其弹性阶段曲线与第1类的相同；进入弹塑性阶段后，荷载上升速率缓慢，且位移增加速率变大，表现出很好的延性；在经过峰值点后，波动范围较小且荷载仍可以保持相对稳定。

3) 第3类，荷载-位移曲线分为弹性阶段、弹塑性上升段、峰值后下降段和平稳后的突变段。其弹性段曲线变化与第1类和第2类的相同，在进入弹塑性阶段后，荷载上升速率大幅度降低，上升速率与钢管的直径呈正相关；对比其他2类，此类曲线的峰值较为明显，经过峰值点后曲线缓慢下降，在经过一定位移后荷载陡降。

由图4可以观察到，无论是钢管内填充水泥还是外缠碳纤维布，均可以提升试件的抗弯承载力最大值和抗弯刚度，其中钢管+水泥+CFRP布试验组中刚度提升最为明显，刚度提升效果从大到小依次为IV组、III组、II组、I组；在I、II、III组中，刚度越大，其达到峰值荷载所用的跨中位移越小，而在第III组中，刚度越大，达到峰值荷载所需的跨中位移越大，这可能是因为CFRP可以在一定程度上使试件的刚度与延性呈正相关；钢管组与钢管+CFRP布试验组中试件破坏形式几乎一致，曲线形式也近似一致，可见二者并不能很好地发挥CFRP布与钢管的抗拉性能。钢管+水泥组试件表现出较好的延性，侧面鼓曲现象不明显。钢管+水泥+CFRP布组试件表现为高刚度，但由于外缠CFRP布拉断后，会出现承载力陡降现象。

2.3 荷载-位移-应变曲线分析

图5所示为将32 mm口径钢管与不同材料相互组合所测得的荷载-位移-应变曲线。图5中，N为荷载，εs、εc、εcf分别为钢管、水泥和CFRP的纵向应变。从图5可得到以下结论：

1) 对于钢管试验组试件，其纵向拉伸应变在加载的弹性阶段缓慢上升，在试件进入弹塑性阶段后迅速增大，应变曲线与荷载-位移曲线较吻合。

2) 在钢管+水泥试验组中，在弹性阶段，水泥的纵向应变变化速率由快到慢，其曲线呈上凸状，钢材的纵向应变变化速率由慢到快，其曲线呈下凸状；两者的应变曲线在试件从弹性阶段进入弹塑性阶段时速率发生变化，水泥应变曲线变化速率先变缓再增加，钢材的应变曲线变化速率与其弹性阶段相比略微缓慢；两者的应变曲线在试件荷载平稳段时的变化趋势较一致，表明两者可以较好地协同工作。

3) 在钢管+CFRP布试验组中，与钢管组类似，钢管与CFRP布可以很好地协同工作。

4) 在钢管+水泥+CFRP布试验组中，弹性阶段水泥应变曲线呈上凸状，钢管与CFRP布的应变曲线呈下凸状；在进入弹塑性阶段后，水泥应变速率先下降再上升，钢管与CFRP布应变速率上升速度变缓，最后，三者应变曲线变化相对平稳，说明这三者可以较好地协同工作。

由图5还可知：在钢管+水泥试验组中，从弹性阶段到弹塑性阶段前期，水泥应变曲线呈现为上凸型，即变化速率先快后慢。考虑到水泥自身的性质，在灌注过程中，不可避免地会产生微小气泡，随着荷载增大，钢管内的水泥不断被压实，在钢管的限制作用下，形成了三向受压状态，使得水泥纵向应变速率由大变小，而钢管在与水泥逐渐贴合的过程中，两者应变变化速率较为一致，即二者可较好地协同工作。在钢管+水泥+CFRP布组中，当试件处于弹塑性平稳段时，可以观察到三者能较好地协同工作。

2.4 抗弯承载力最大值

不同材料对于钢管的抗弯承载力最大值的提升和提升比例分别见表4和表5。

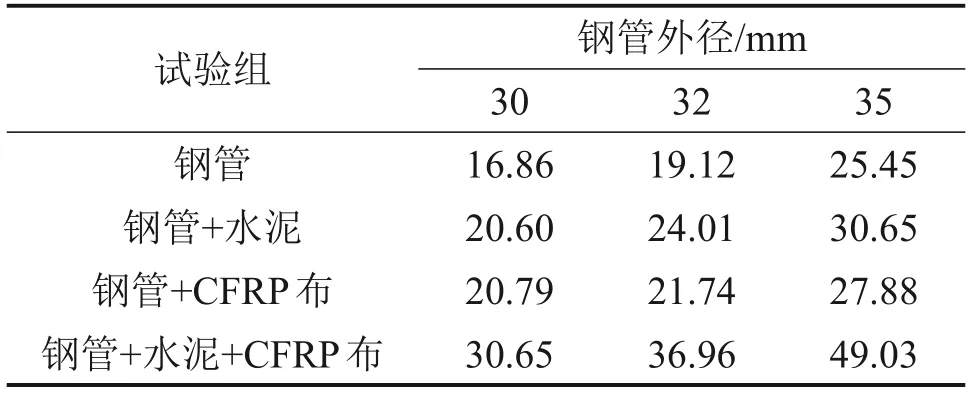
表4 抗弯承载力最大值对比Table 4 Comparison of the maximum bearing capacity kN

表5 抗弯承载力最大值提高比例Table 5 Increasing ratio of the maximum bearing capacity%

综合分析表4和表5可知，只有水泥作用时对钢管的抗弯承载力最大值的提升幅度整体比只有CFRP布作用于钢管时的高，这是因为钢管与CFRP布组合时并不能很好地承受荷载带来的压力而被压溃，不能充分发挥CFRP布的拉伸性能。当钢管、水泥、CFRP这3种材料组合时，极限承载能力大幅提高，相比于钢管组提高约90%，组合结构既可以较好地发挥CFRP布的抗拉伸性能，也可以较好地发挥水泥的抗压性能。

3 有限元模型的建立及模型验证

3.1 材料本构模型的选取

本文的数值模拟采用ABAQUS软件，对试件进行三点弯曲试验模拟。

3.1.1 钢材

钢材的应力-应变关系模型选自ABAQUS中提供的弹塑性模型，满足Von Mises屈服准则。选用方钢管的弯角处存在圆化现象，这种情况会大幅度提高钢材的抗拉强度以及屈服强度，需进一步处理才可以应用到数值模拟软件中。

3.1.2 水泥

基于《混凝土结构设计规范》[23]中建议的单轴本构关系建立水泥的本构模型，在ABAQUS软件中使用的计算模型为软件提供的混凝土塑性损伤模型。塑性损伤模型是通过引入损伤引子来对混凝土的弹性刚度进行折减，将塑性模型和线性损伤模型相结合，将混凝土的受压破碎和受拉开裂作为主要破坏机理。无论是单轴受拉状态还是单轴受压状态，在开始阶段混凝土都处于弹性阶段，超出弹性范围后开始出现塑性损伤即刚度减小。

3.1.3 CFRP

碳纤维布是各向异性材料，仅在纤维方向上承受拉力。本试验选取的碳纤维布为300 g一级的单项碳纤维布，纤维方向沿纵向分布，可认为其只承受纤维方向的拉应力。在达到极限拉应力时，纤维发生脆性断裂(断裂前纤维形变满足胡克定律)，断裂后纤维失去承载力。本文使用壳单元来模拟CFRP材料，并利用复合材料中的传统壳(conventional shell)建模来实现铺层的功能。在传统壳单元中，可以定义材料的铺层方向、纤维方向以及每层材料的厚度。使用Hashin Damage来模拟CFRP材料的损伤发展和失效破坏过程。

3.2 单元选取、网格划分以及接触和边界条件

有限元分析共12组模型，本文仅以外径为32 mm的方钢管以及其对照组为例进行分析。用于三点弯曲试验的CFRP-钢管混凝土构件由钢管、水泥、CFRP布和用来加载的压头4个部分组成。水泥和钢管采用8节点缩减积分三维实体单元(C3D8R)；CFRP布采用4节点缩减积分壳单元(S4R)，厚度方向采用3个积分点的Simpson积分；用来加载的装置采用解析刚体模拟。

钢管与水泥之间采用法向硬接触，切向采用罚函数接触，摩擦因数取0.6；CFRP布与钢管之间的接触采用“tie”绑定接触，压头与CFRP布或者钢管之间采用法向硬接触和切向的罚函数接触，摩擦因数取0.2。将构件下方的2个解析刚体设置参考点Rp并使其完全固定，上方解析刚体设置参考点Rp1，向y斜轴负向移动，以此来完成三点弯曲试验。

具体网格划分以及边界条件见图6。

图6 网格划分和边界条件Fig.6 Mesh dividing and boundary conditions

3.3 计算结果

3.3.1 荷载-位移曲线对比

图7所示为有限元计算所得抗弯承载力最大值与试验结果的比较。

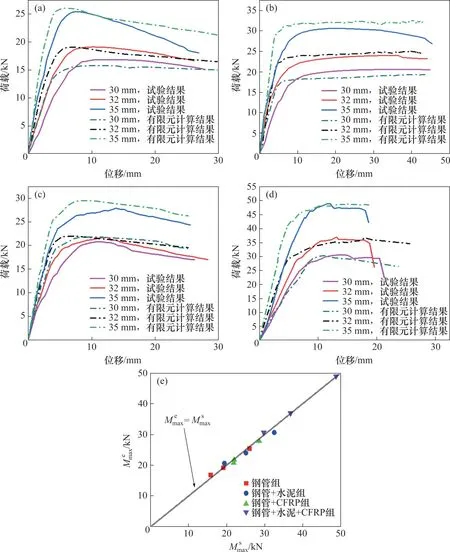
图7 Mmax有限元计算结果与试验结果对比Fig.7 Comparisons between predicted results and tested results of Mmax

从图7可以看出，Mmax有限元计算结果与试验结果吻合较好。对于有水泥填充组，在灌注水泥时，由于钢管的尺寸较小，人工灌注振捣过程中没有完全将小型气泡排除。对于无水泥填充组，由于现实材料存在初始缺陷，故有限元计算所得初始抗弯刚度偏大。

3.3.2 试验破坏模式有限元计算结果与实验结果对比

试验破坏模式有限元计算结果与实验结果对比见图8。由图8可以观察到：1) 钢管组的破坏形式大致相同，都为上方压溃以及侧面严重鼓曲；2) 钢管+水泥组体现出上方轻微压溃以及侧面轻微鼓曲；3) 在外缠CFRP布的2组实验中，无水泥填充时，CFRP布底部拉伸不明显，且底部CFRP布中部有向内聚拢现象，没有很好地发挥自身的抗拉伸性能，而在填充水泥之后，侧面CFRP布拉伸破坏区域范围减小，底部CFRP布拉伸性能发挥得更充分。

图8 破坏模式有限元计算结果与试验结果对比Fig.8 Comparison of finite element calculated results and tested results of deformed modes

4 参数分析

本文在12组正式试验的基础上，添加4组正交试验，以验证模型的准确性。以此为基础，利用现有模型进行3组参数分析。选取CFRP厚度为1 mm、钢管外径为32 mm的CFRP-方截面钢管混凝土试件。

钢管与水泥之间的黏结性能是其保持良好的工作状态的基础。白亚东等[24]将钢管混凝土的黏结原理总结为以下3点：一是混凝土与钢管之间的化学胶着力，受混凝土的水灰比和材料品种的影响；二是两者之间的机械咬合力，通过改变两者之间的粗糙程度来改变机械咬合力；三是两者之间的摩擦力，当钢管与混凝土的界面之间产生较大的滑动时，摩擦力开始占主导地位。因此，在第1组参数分析实验中，通过改变钢管与水泥之间的摩擦因数来反映黏结能力对抗弯承载力最大值的影响。取切向罚函数的摩擦因数分别为0.3、0.6和0.9。

在第2组参数分析实验中，考虑在不改变钢材和CFRP布的性质和厚度的前提下，水泥强度对试件的抗弯承载力最大值的影响。取水泥立方体试块抗压强度分别为30、40和50 MPa。

在第3组参数分析实验中，考虑在不改变钢材性质及水泥强度的前提下，CFRP布的厚度对试件抗弯承载力最大值的影响。取CFRP布的厚度分别为1、2和3 mm。

黏结性能、水泥强度以及CFRP布厚度对抗弯承载力最大值的影响见图9。

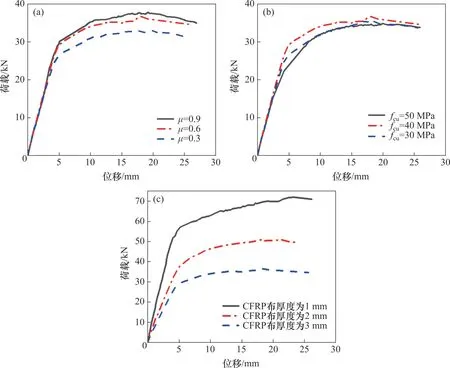
图9 参数分析Fig.9 Parameter analysis

从图9可以得到以下结论：1) 改变摩擦因数和水泥强度对构件的初始抗弯刚度并没有太大影响，而改变CFRP布的厚度对结构的初始抗弯刚度影响较大。2) 改变摩擦因数可以改变试件的抗弯承载力最大值，但对其影响程度并不明显。相对于摩擦因数为0.3的试件，摩擦因数分别为0.6和0.9的试件的抗弯承载力最大值分别提升了11.6%和14.7%。3) 当水泥强度增大至50 MPa时，试件强度反而降低，而当水泥强度分别为30 MPa和40 MPa时，抗弯承载力最大值差别不大，说明水泥强度对抗弯承载力最大值的影响并不明显。4) 改变CFRP布的厚度可以极大地提升试件的抗弯承载力最大值，相较于CFRP厚度为1 mm的试件，CFRP布厚度为3 mm和2 mm的试件抗弯承载力最大值分别提升了38.7%和95.7%。