集中配筋连接预制剪力墙抗震性能试验研究

肖扬，卢谦，罗小勇,2，陈林松，程俊峰,2，张璧玮

(1.中南大学 土木工程学院，湖南 长沙，410075；2.湖南省装配式建筑工程技术研究中心，湖南 长沙，410075；3.中交第二航务工程局有限公司技术中心，湖北 武汉，430014)

装配式混凝土(PC)结构因具有施工周期短、节能环保和节省人力等优点而得到广泛应用。PC剪力墙结构作为PC结构体系中的主要组成部分之一，契合“住宅产业化”的政策导向，在我国得到了广泛发展与应用[1-3]。PC剪力墙结构体系中存在大量的水平和竖向接缝，接缝的连接形式是影响其整体性和抗震性能的关键因素之一。目前，PC剪力墙接缝的连接形式主要有后浇带连接、套筒灌浆连接、预留孔浆锚搭接、螺栓连接、后张预应力连接、键槽连接等[4]。钱稼茹等[5]对竖向钢筋采用不同的连接方式的预制剪力墙进行了拟静力试验，发现利用普通混凝土现浇带连接的预制剪力墙试件的抗震性能和延性相对较差，而利用套筒灌浆连接能有效传递墙体竖向应力。陈云钢等[6-7]通过预留孔浆锚搭接剪力墙试验发现预留孔浆锚搭接连接剪力墙的抗震性能与现浇墙的抗震性能相近。BRIAN等[8-9]对采用普通钢筋和后张法预应力钢绞线连接的预制剪力墙混合接缝进行试验，发现普通钢筋屈服耗能，而预应力钢绞线能使结构具有足够承载力和侧向位移的延性。众多研究表明，目前采用的装配式剪力墙连接方法基本上能获得较好的连接效果，装配试件与现浇试件的抗震性能相当，但这些连接方法大多存在施工精度要求高、容错率低以及施工难度大等困难。一些学者提出采用竖向连接方式施工。张微敬等[10]对4片设置现浇边缘构件的单片预制圆孔板剪力墙进行了拟静力试验，发现预留圆孔钢筋浆锚搭接可以实现应力的有效传递，预制剪力墙和现浇剪力墙的抗剪承载力和延性相近。周剑等[11]开展了预制混凝土空心模剪力墙抗震性能试验，发现采用插筋连接可以有效传递钢筋应力，且双排插筋空心模剪力墙的整体抗震性能略好于采用单排插筋的墙的整体抗震性能。上述插筋连接解决了套筒灌浆连接和预留孔浆锚搭接施工困难等问题，但其预制剪力墙边缘构件现浇且连接钢筋布置较多(孔洞率高)，仍然存在湿作业量大以及锚固长度过长等不足。因此，将剪力墙的边缘构件预制、连接钢筋在大间距的通长圆孔内集中布置，并在搭接处使用高强高韧材料——超高性能混凝土(UHPC)[12-15]，能减少湿作业和锚固长度，同时能够保证连接段强度。为此，本文作者在预制空心模剪力墙和预制圆孔板剪力墙插筋连接的基础上，提出一种施工便捷、湿作业较少以及钢筋锚固长度较短的竖向连接技术——集中配筋连接，并通过拟静力试验，研究试件的破坏和裂缝发展机理以及极限承载力、延性、耗能能力、刚度退化、钢筋应变以及竖缝等对试件抗震性能的影响，利用数值模拟验证试验结果，并对参数进行分析，评价采用集中配筋连接的装配式剪力墙的抗震性能。

1 预制剪力墙集中配筋连接试验

1.1 集中配筋连接工艺

预制剪力墙的集中配筋连接如图1所示。在大间距集中布置的通长圆孔内，通过间接搭接[16-18]大直径钢筋、搭接段后浇UHPC来实现有效连接，从而传递应力。相较于预留孔浆锚搭接，集中配筋连接的主要受力钢筋显著减少，而UHPC具有强度高、与钢筋黏结性好、自密实以及能减小钢筋锚固长度等特点，可以满足集中配筋连接技术在搭接段对于高性能材料的需求。

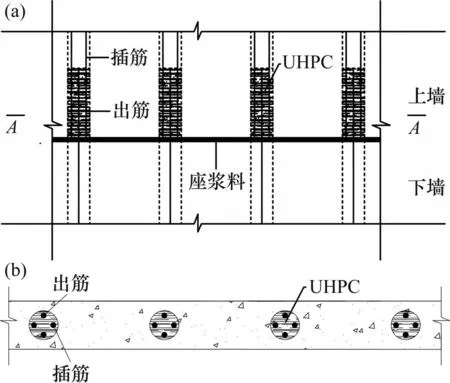
图1 集中配筋连接示意图Fig.1 Illustration of concentrated reinforcement

集中配筋连接技术是通过下部基础(墙体)的出筋插入上部预制剪力墙预留的通长圆孔内，从上部墙体顶端圆孔插入竖向连接钢筋，与下部基础(墙体)的出筋在圆孔内实现间接搭接，随后在搭接段和非搭接段分别灌注UHPC和普通混凝土，从而将上下墙连成一个整体。设计时。可以根据实际情况对连接钢筋的直径以及圆孔的位置、直径进行相应调整，以满足实际工程中对结构设防烈度和结构承载力的不同需求，从而为集中配筋连接的预制剪力墙在实际工程中的应用提供技术支撑。

1.2 试件设计

试验设计了4片足尺剪力墙试件，其中，SW1为现浇剪力墙试件，PW1-PW3为采用不同接缝形式的集中配筋连接预制剪力墙试件。预制剪力墙试件由预制剪力墙与预制基础梁组成，基础梁长×宽×高为2 500 mm×1 300 mm×500 mm。剪力墙高×宽×厚为3 000 mm×2 000 mm×200 mm，高宽比为1.5，轴压比为0.1。水平接缝设置在墙体底部，竖向接缝设置在墙体中部，水平接缝和竖向接缝宽度均为20 mm。各试件编号及主要变化参数如表1所示。

表1 试件编号及主要变化参数Table 1 Specimen number and main parameters

所有试件墙体的混凝土强度等级为C30，基础梁的混凝土强度等级为C40，所用钢筋的等级均为HRB400。试件SW1按二级抗震[19]剪力墙设计，其墙体分布钢筋双层布置，用梅花式点布的拉筋拉结成一个整体，墙体两端360 mm范围内设置暗柱，其墙身钢筋与基础梁钢筋绑扎为一体，整体浇筑，竖向受力钢筋总面积为2 788.8 mm2；试件PW1、PW2和PW3墙身竖向钢筋在水平接缝处断开，不与基础梁连接，每片墙内另外设置822(总面积为3 041 mm2)的连接钢筋与基础梁间接搭接，使预制墙和现浇墙主要受力钢筋的面积基本一致，以达到不降低预制墙受压承载力的目的[20]，此时，预制试件的集中配筋率(即预制墙集中布置的连接钢筋面积与现浇竖向受力钢筋面积之比)为109%(即3 041.0/2 788.8)。试件的几何尺寸及配筋见图2，接缝构造见图3。

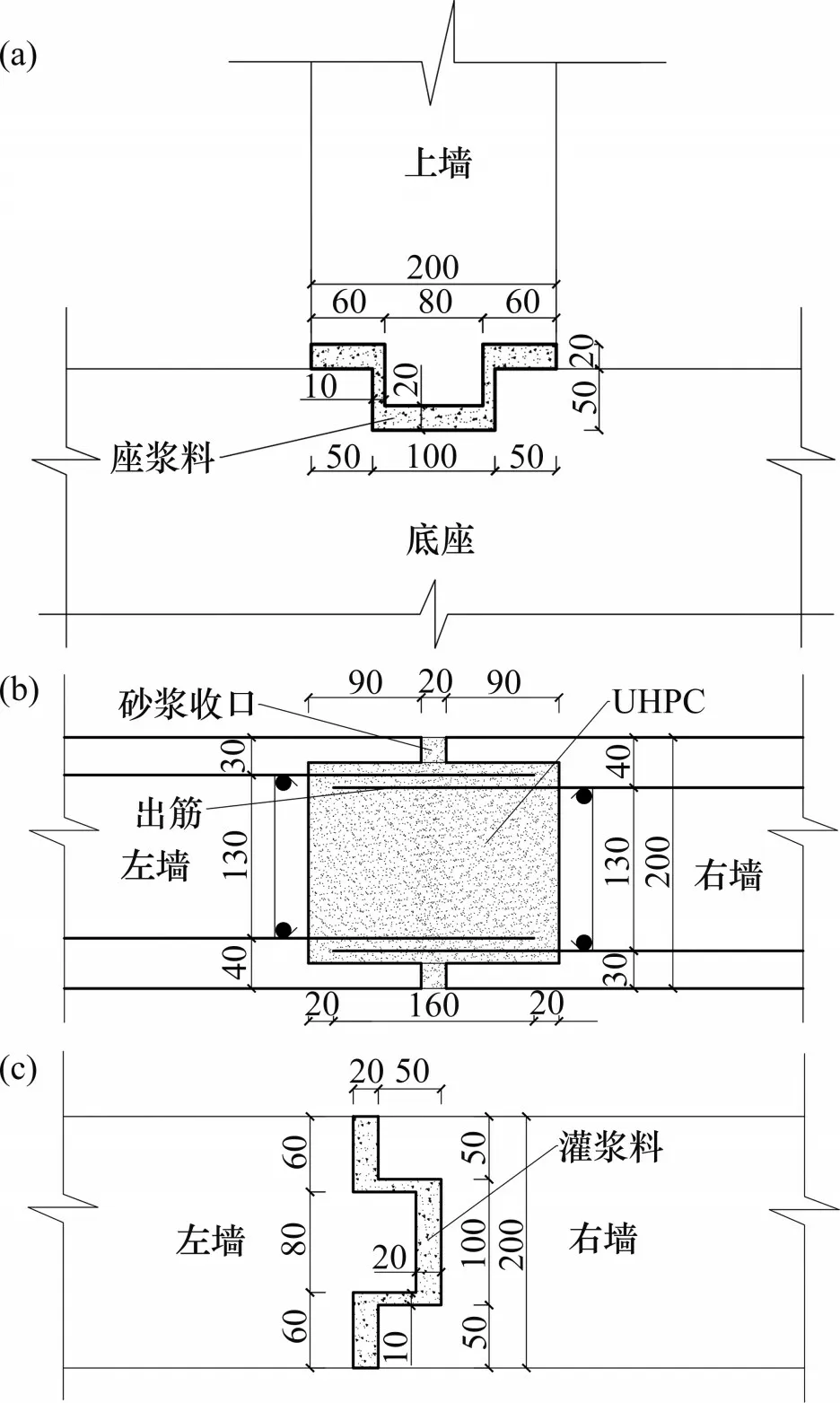
图3 接缝构造Fig.3 Seam construction

预制墙中预留的通长圆孔直径为120 mm，圆孔中心距均为500 mm，端部圆孔中心距离墙边250 mm。预制墙的每个圆孔中插入2根直径为22 mm的通长连接钢筋，预制基础梁内预埋4根直径为22 mm的U形钢筋，伸出基础梁顶面400 mm。预制墙安装到位后，从墙顶部圆孔处浇筑UHPC灌满搭接段，非搭接段随后浇筑混凝土，搭接长度为400 mm，大于12.6d[21](其中，d为搭接钢筋直径，12.6d即277.2 mm)。

1.3 材料性能

UHPC中钢纤维的直径为0.12 mm，平直镀铜纤维长为8 mm，钢纤维拌合比为2%，水灰比为0.092。试验测得边长为100 mm的UHPC立方体试块平均抗压强度，其中，预留孔平均抗压强度为135 MPa、竖缝平均抗压强度为150.1 MPa；边长为150 mm的混凝土立方体试块平均抗压强度为31.5 MPa；边长为70.7 mm的座浆料立方体试块平均抗压强度为48.5 MPa；长×宽×高为40 mm×40 mm×160 mm的灌浆料长方体试块平均抗压强度为101.0 MPa。HRB400钢筋的力学性能实测值见表2。

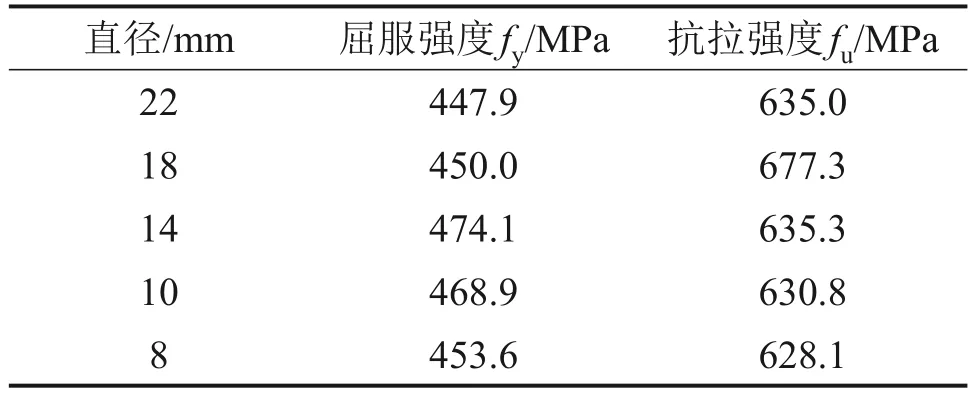
表2 钢筋HRB400的力学性能Table 2 Mechanical properties of HRB400 steel bar

1.4 加载和测试方案

本试验在中南大学高速铁路建造技术国家工程研究中心进行，使用20 MN级重载多功能结构实验系统。试验时，轴向压力由竖向作动头施加，轴压比为0.1，通过钢分配梁将荷载均匀分布到剪力墙顶部，保持试件轴压力在试验过程中恒定。剪力墙水平荷载使用FCS电液伺服加载系统施加，水平推力由量程为1 MN的水平作动器直接施加，水平拉力由4根直径为35 mm的精轧螺纹钢与厚钢板组成的加载体系间接施加；在螺纹钢下设置夹具，防止剪力墙发生扭转；底座两侧用量程为1 MN的千斤顶顶紧，防止试件产生滑移，试验加载装置[22-24]如图4所示。

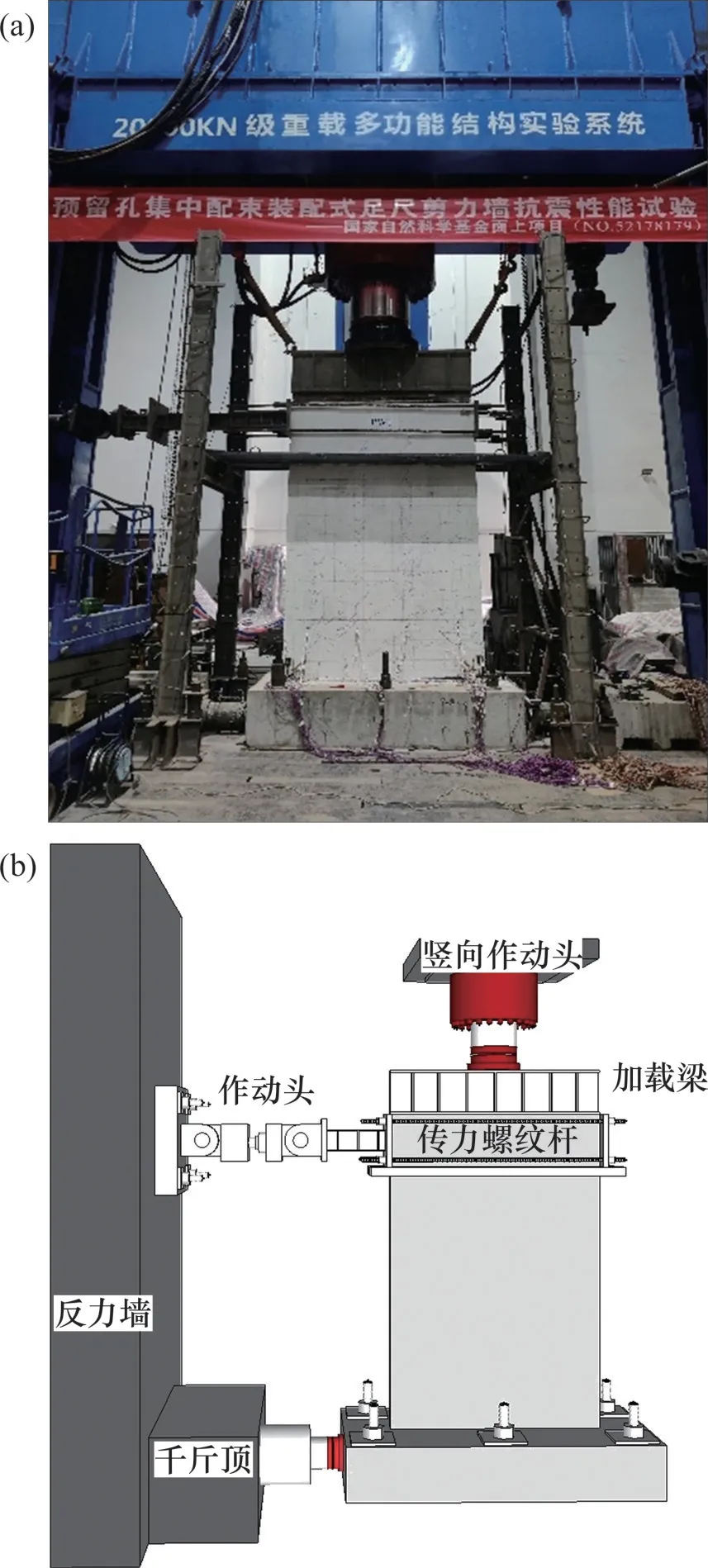
图4 试验加载装置Fig.4 Test loading device

试验正式加载前先预加载1次，在消除初始非弹性变形的同时保证整个试件的加载装置连接可靠，正式加载时的水平荷载由力控制加载，加载级差为100 kN。每级荷载往复加载1次。试件屈服后由位移控制加载，加载级差为1倍屈服位移，每级加载循环2次，当水平荷载降至峰值荷载的85%时停止试验。试验时，水平作动器先推后拉，规定推力为正，拉力为负。

1.5 观测内容和测点布置

试验中测量了墙体的水平荷载、位移和钢筋应变。水平荷载通过作动器上的荷载传感器直接读取。试件PW2的位移测点布置如图5所示。在D1处测量基础梁的水平滑移，在D2至D5处测量墙体不同高度处的水平位移，在D7和D8处测量墙角抬高，在D9和D11处测量竖缝的水平张裂，在D10和D12处测量竖缝的竖向错动。试件PW2的钢筋应变测点布置如图6所示。图6中，S1～S18为竖向构造钢筋应变片所在位置，S19～S34为连接钢筋应变片所在位置。其他试件的位移和钢筋应变测点布置与试件PW2的基本相同。试验时，所有试验数据通过数据采集系统采集并实时监控，加载时，记录试验数据并同时测绘裂缝分布。

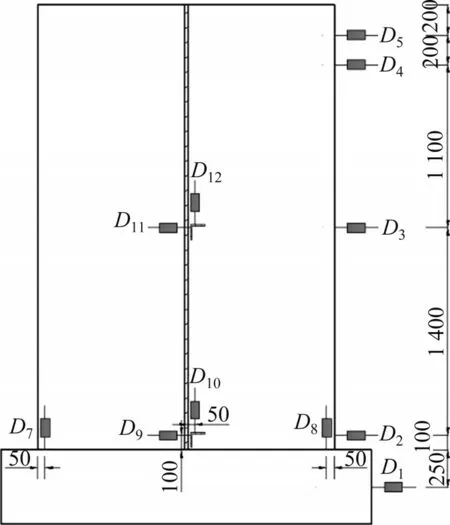
图5 位移测点布置Fig.5 Layout of displacement measurement points

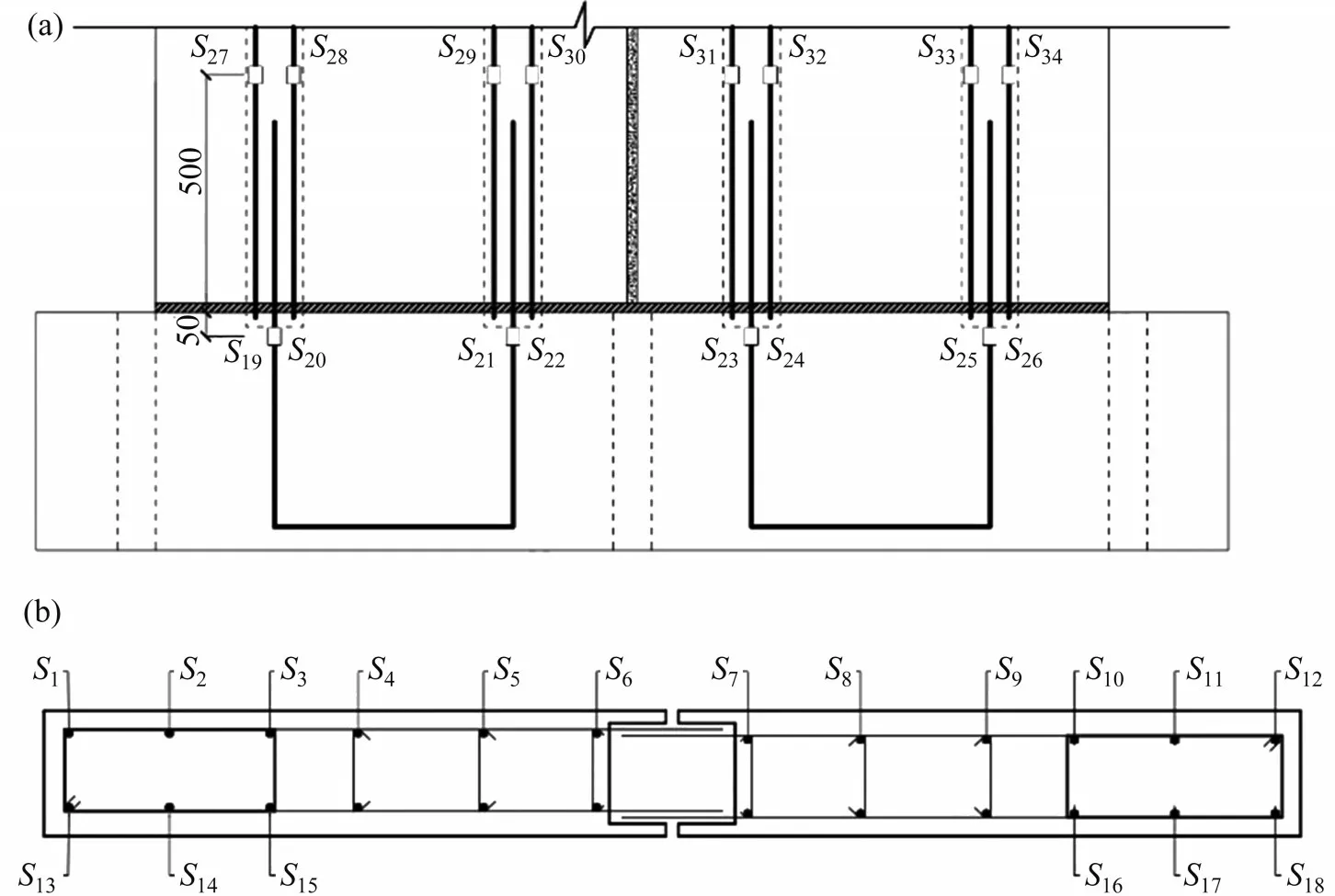
图6 钢筋应变片布置Fig.6 Layout of steel bar strain gauges

2 试验现象及破坏形态

各试件在加载过程中具有相近的破坏规律，均经历了墙身混凝土开裂、受拉钢筋屈服、墙脚混凝土压溃、承载力下降等几个主要阶段，试件最终的破坏模式均为弯剪破坏，最终破坏形态为墙脚混凝土压溃破坏。预制试件破坏后，竖缝界面的张裂和错动较小，预留孔底部UHPC出现少量裂缝，但连接钢筋在UHPC中仍锚固良好。

2.1 试件SW1

当试件SW1的水平荷载加载到280 kN时，在墙体根部出现第1条水平裂缝，长度为30 mm，试件开裂。当水平荷载达到480 kN时，墙体根部处水平裂缝贯通，缝宽为0.1 mm，此时，剪力墙加载点水平位移为5.9 mm，试件边缘暗柱的纵筋屈服，随后转为位移控制加载。当水平位移达到12.16 mm时，裂缝大量出现，墙体高度1.6 m内新增3条45°斜裂缝，裂缝延伸至墙体中间部分。当水平位移达到29.97 mm时，原有裂缝不断延伸拓宽，最长斜裂缝延伸至受压区墙角，此时，墙身斜裂缝最大宽度为1.6 mm，受压区混凝土出现受压裂缝。当水平位移达到66.25 mm时，两侧墙角混凝土大面积剥落，分布钢筋外露、纵筋鼓曲，墙角抬高12.87 mm，水平荷载降低至峰值的81.2%，试件被破坏，试件SW1的整体破坏形态和裂缝分布见图7(a)和图7(b)。

图7 试件整体破坏形态和裂缝分布Fig.7 Overall failure pattern and crack distribution of specimen

2.2 试件PW1

试件PW1整体破坏形态和裂缝分布如图7(c)和图7(d)所示。当试件PW1的水平荷载加载到240 kN时，墙体与键槽接触面开裂，裂缝长度为200 mm；当水平荷载达到320 kN时，基础梁与键槽接触面出现裂缝；当水平荷载达到400 kN时，键槽处水平裂缝贯通，剪力墙开始出现滑移现象；当水平荷载达到450 kN时，端部预留孔内连接钢筋受拉屈服，随后转为位移控制加载，此时，剪力墙加载点水平位移为4.97 mm，墙体受拉区0.9 m和1.1 m高度处出现2条新的水平裂缝，缝宽为0.1 mm；当水平位移达到10.21 mm时，裂缝大量出现，墙体高度1.8 m处出现超长斜裂缝延伸至受压区键槽座浆层，座浆层裂缝最大宽度达3.2 mm，受拉侧墙角开始出现抬升现象，原水平裂缝开始向斜向发展，中间预留孔孔壁位置出现交叉斜裂缝；当水平位移达到55.31 mm时，墙角抬高25.48 mm，受压区墙角混凝土大面积压溃，水平荷载降低至峰值的75%，试件被破坏，此时，预留孔下端UHPC出现少量裂缝，但连接钢筋在UHPC中仍锚固良好(连接钢筋的锚固状态见图8)。

图8 连接钢筋锚固状态Fig.8 Anchoring conditions of connecting steel bar

2.3 试件PW2

试件PW2在开裂和屈服阶段的裂缝发展规律与试件PW1的裂缝发展规律基本相似，只在峰值和破坏阶段略有不同。当水平位移达到9.54 mm时，墙端产生的5条水平裂缝，经边缘预留孔后45°斜向下发展，一直延伸到竖缝区域，此时，墙体竖缝区0.4 m高度处出现水平裂缝，中间预留孔孔壁位置出现交叉斜裂缝。当水平位移达到14.43 mm时，边缘预留孔的孔壁位置内出现交叉斜裂缝。随着水平位移不断增大，原有裂缝不断延伸拓宽，交叉斜裂缝沿孔壁不断向墙体顶部发展，但始终没有超长贯穿斜裂缝。当水平位移达到55.23 mm时，墙角抬高29.1 mm，受压区墙角混凝土压溃，水平荷载降低至峰值的79%，试件被破坏。连接钢筋锚固状态与试件PW1的锚固状态相似，在整个加载过程中，竖缝的竖向错动最大值接近0.3 mm，水平张裂最大值为1.0 mm。整体破坏形态和裂缝分布见图7(e)和图7(f)，竖向接缝两侧墙体的变形(δ)相对墙体水平位移(Δ)变化曲线见图9(a)。

图9 竖向接缝两侧墙体的相对位移变化曲线Fig.9 Relative displacement curves of walls on both sides of vertical joints

2.4 试件PW3

试件PW3在加载过程中的破坏规律与试件PW2的破坏规律基本相似。由于加载时试件PW3的负向刚度比正向刚度略小，即在相同荷载作用下，反向拉力加载对试件PW3产生的变形比正向加载更大，因此，在实际加载过程中，以负向拉力加载时连接钢筋受拉屈服的剪力墙加载点水平位移为屈服位移，即当水平荷载加载到-480 kN时，钢筋受拉受拉屈服，转为位移控制加载。当水平位移达到43.73 mm和-54.57 mm时，受压区墙角混凝土大面积剥落，暗柱箍筋外露，正、负向荷载分别下降至峰值荷载的81.8%和81.4%，墙角抬高19.89 mm，试件被破坏。预留孔内钢筋锚固状态与试件PW1的锚固状态相似，在整个加载过程中，竖缝的竖向错动最大值接近2 mm，水平张裂最大值为4.5 mm。整体破坏形态和裂缝分布见图7(g)和图7(h)，竖向接缝两侧墙体的变形(δ)相对墙体水平位移(Δ)的变化曲线见图9(b)。

对比图7中4片试件的裂缝分布可知：现浇试件相对预制试件的裂缝发展更充分，具体表现在贯穿斜裂缝更多、裂缝发展的高度更高、密度更大，但预制试件预留孔壁处存在交叉斜裂缝(推测是预留孔壁处混凝土较薄所致)，且预制墙体在键槽水平接缝贯穿后相对基础梁存在滑移现象，滑移和交叉斜裂缝的生成都会消耗一部分能量，故预制试件的裂缝发展整体上没有像现浇试件裂缝那样发展充分。对比图7中试件PW1与PW2、PW3的裂缝分布可知：竖缝的存在使预制试件贯穿斜裂缝减少，裂缝分布密度降低，键槽座浆层贯穿破坏程度降低，这是因为竖缝所用UHPC和灌浆料均为高强材料，能有效抑制裂缝的产生和发展。对比试件PW2和PW3的试验现象可知：试件PW3相对试件PW2的裂缝发展更充分，表明竖缝形式为U形键槽的剪力墙试件具有更强的耗能能力。由图9可知：试件PW2竖缝两侧墙体的变形比PW3的变形更小，表明竖缝形式为UHPC出筋搭接的剪力墙具有更好的整体性。

3 试验结果及分析

3.1 滞回曲线

各试件加载点水平荷载(F)-位移(Δ)曲线(滞回曲线)如图10所示。从图10可见：4个试件的滞回曲线变化趋势基本相同，形状较饱满，大体上为“弓形”，表明4个试件的耗能能力均较强；4个试件的滞回曲线均存在一定的捏缩现象，这主要是因为钢筋和混凝土界面存在黏结滑移，而预制试件的捏缩程度明显比试件SW1的高，这主要是键槽座浆层贯通后剪力墙的滑移所致。试验时，因试件PW3正负向刚度略有差异，导致其曲线不对称。由图10可知：试件SW1滞回曲线包络图面积最大，预制试件中PW1滞回曲线包络图面积最大，说明现浇墙的耗能能力最强，整墙的耗能能力比设有竖缝墙体的耗能能力更强。

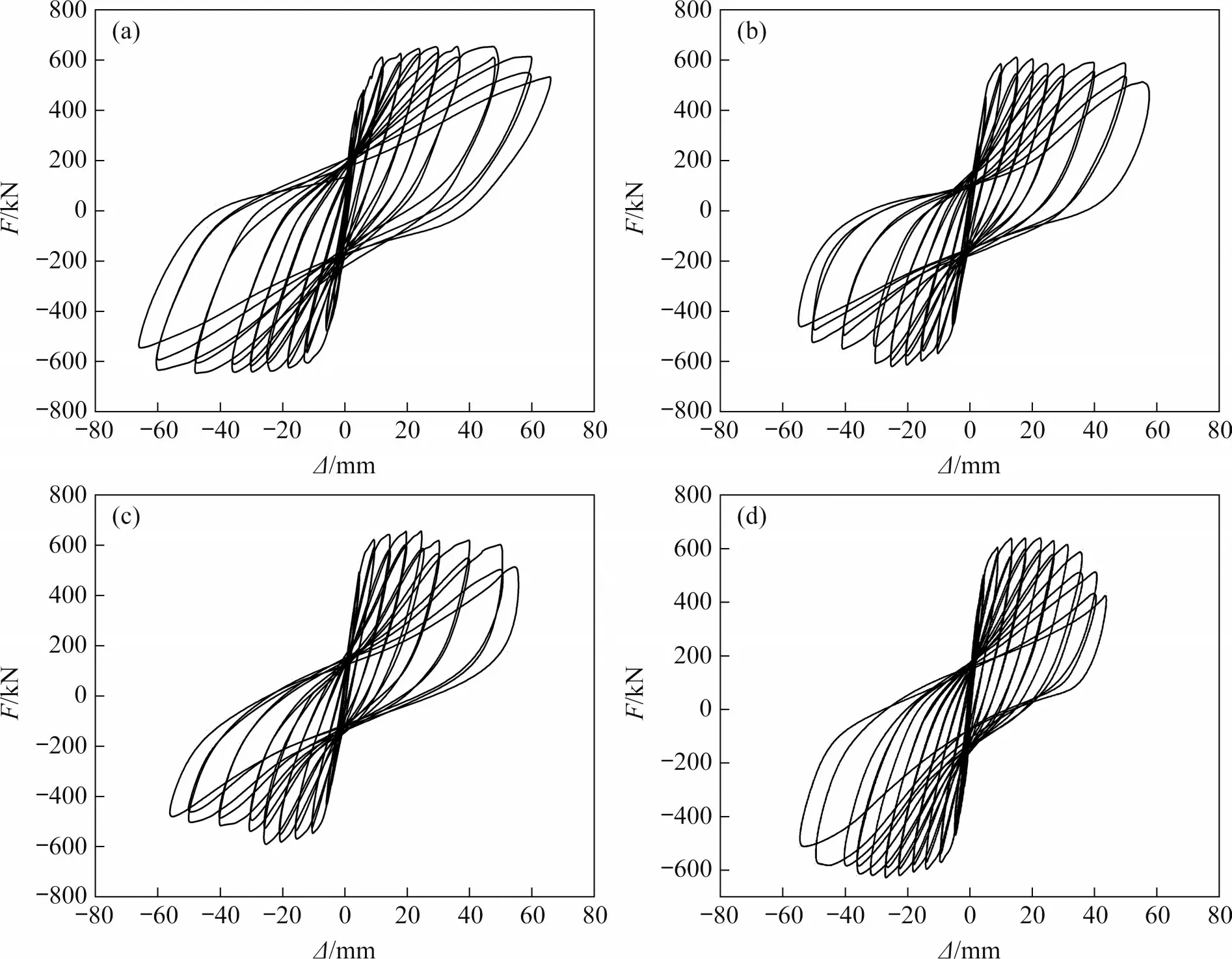
图10 各试件滞回曲线Fig.10 Hysteresis curves of each specimen

3.2 骨架曲线

各试件骨架曲线的对比见图11。由图11可知：4个试件骨架曲线的走势基本一致，均经历了弹性、屈服、强化、破坏4个阶段；弹性阶段直线斜率基本相同，说明4个试件初始刚度接近；4个试件均经历了较长的屈服台阶才进入破坏阶段，表明试件均具有良好的延性。对比4条骨架曲线可知：试件SW1强化阶段后的骨架曲线基本在试件PW1、PW2和PW3的上方，表明现浇剪力墙的承载力比预制剪力墙的高；各阶段试件PW2和PW3的骨架曲线基本上与试件PW1的骨架曲线重合，表明竖缝对剪力墙承载力的影响并不大，其中，试件PW3的正向刚度比负向刚度略大，导致其正向骨架曲线经过屈服平台后相对负向下降较快。

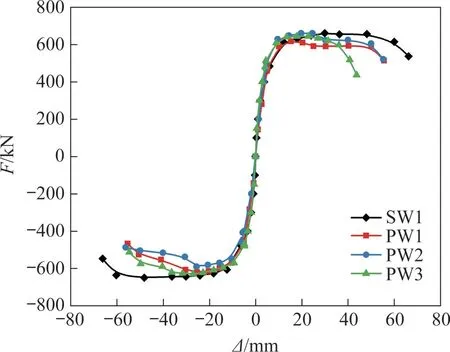
图11 各试件骨架曲线Fig.11 Skeleton curves of each specimen

3.3 承载力、变形能力和延性

试件各特征点的荷载和位移、试件的位移角以及延性系数见表3。从表3可知：预制试件的开裂荷载和屈服荷载比SW1的略小，表明在试验加载前期，不同接缝形式的集中配筋连接预制剪力墙抵抗外部荷载的能力与现浇墙相比偏弱；试件PW1的峰值荷载相比SW1仅小5.6%，表明在相同轴压下，不同接缝形式的集中配筋连接预制剪力墙的承载力与现浇墙的承载力相近。表3中预制试件的极限位移角均在1/50左右，大于1/120[25]，说明本类型的预制墙有较强的变形能力。预制试件的延性系数均大于8，屈服后变形能力大，这是因为键槽接缝贯通后墙身位移较大，连接钢筋得以充分变形。总体来说，各个试件的弹塑性变形能力均满足规范要求。

表3 试件不同阶段时的水平力和位移Table 3 Horizontal forces and displacements at different stages of specimen

3.4 刚度

4个试件的刚度(K)-位移(Δ)曲线(刚度退化曲线)见图12[26]。由图12可知4个试件的刚度退化趋势基本一致：试件开裂后刚度急剧下降，屈服阶段刚度下降速率变缓，峰值点过后刚度基本持平。试件在各特征点的割线刚度见表4。从表4可知：整体上，试件PW1、PW2和PW3的特征点刚度与试件SW1的特征点刚度十分接近，表明集中配筋剪力墙抵抗变形的能力与现浇墙抵抗变形的能力相近；试件PW3在4个特征点的割线刚度均比其他3个试件的大，说明竖缝形式为U形键槽的集中配筋剪力墙具有更大的抗侧刚度。

表4 试件各特征点割线刚度Table 4 Secant stiffness for each feature point of specimenkN·mm-1

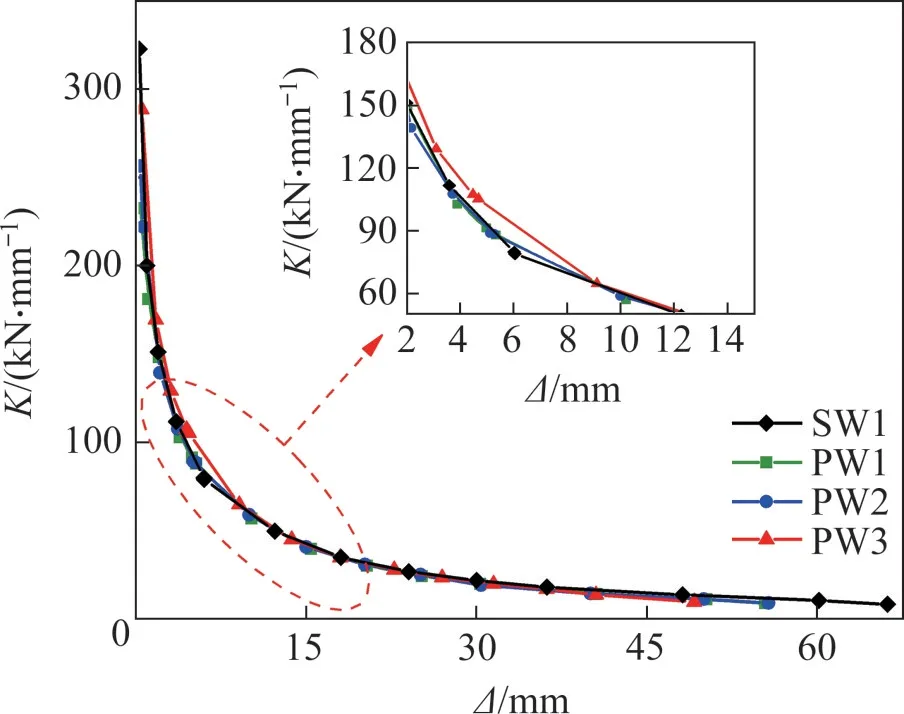
图12 刚度退化曲线Fig.12 Stiffness degradation curves

3.5 耗能能力

利用能量耗散系数E[25]来评定试件的耗能能力。根据试验数据绘制的能量耗散系数(E)-位移(Δ)曲线(耗能曲线)如图13所示。由图13可知：4个试件耗能能力的整体变化趋势一致，开裂后，试件的耗能能力迅速下降，在屈服阶段达到最低点，随后试件进入弹塑性状态；随着往复荷载不断施加，滞回曲线越来越饱满，耗能能力不断增强。对比4个试件各阶段能量耗散系数-位移曲线变化趋势可知：在试验加载初期，现浇墙的能量耗散系数与预制墙的能量耗散系数接近；但在弹塑性阶段，现浇墙的能量耗散系数明显比预制墙的高。对比预制墙的曲线变化趋势可知，试件PW1的曲线始终在PW2和PW3上方，说明试件PW1的耗能能力比PW2和PW3的耗能能力强，即竖缝对剪力墙的耗能能力有一定的削弱作用。

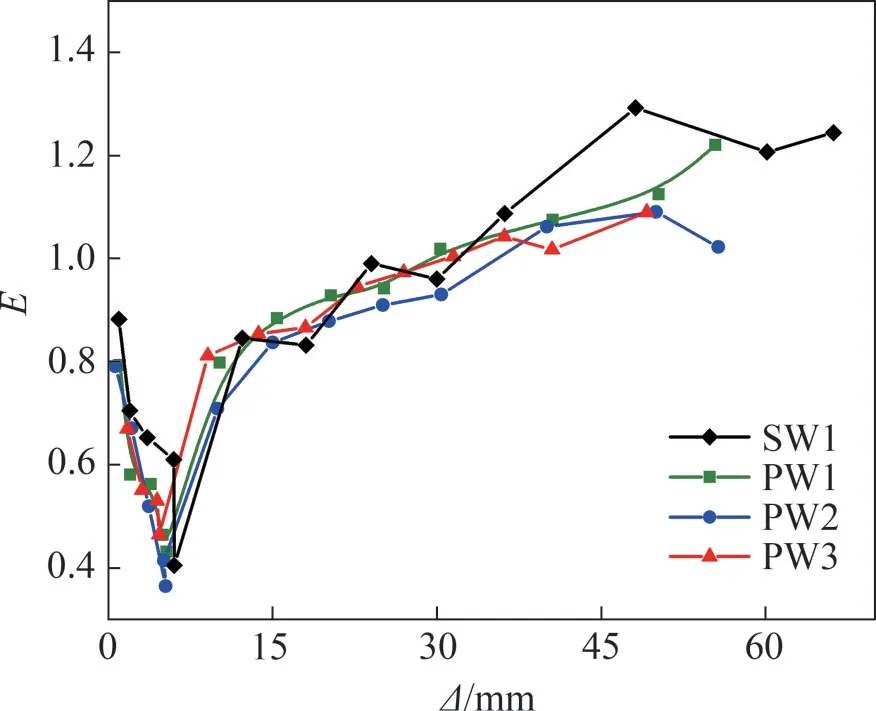
图13 耗能曲线Fig.13 Energy consumption curves

3.6 钢筋应变

试件竖向钢筋的应变(ε)-位置(X)变化曲线如图14所示，其中位置X=0处为墙体中心，位置X=±1 000 mm处分别为墙体的左右两端。由图14可知：4个试件竖向钢筋应变-位置曲线的变化规律基本相同；在试件屈服前，在同一荷载水平下，墙体竖向钢筋应变随位置的变化基本呈1条直线，端部钢筋应变大于中部钢筋应变，符合受弯构件应力分布特征，满足平截面假定；当荷载为400 kN时，试件SW1端部钢筋应变接近2 000με，而预制试件端部钢筋应变均低于500με，证明现浇试件端部纵筋为主要受力钢筋，而同一位置的钢筋在预制墙中仅起构造作用。

图14 竖向钢筋应变-位置曲线Fig.14 Strain-position curves of vertical reinforcement

预制试件预留孔内连接钢筋的应变(ε)-荷载(F)曲线如图15所示。从图15可见：整体上，3个试件应变-荷载曲线的变化规律基本一致；在同一荷载下，边孔内连接钢筋的应变大于中孔内连接钢筋的应变，符合受弯构件应力分布特征。结合图14和图15可知：当荷载为400 kN时，墙身竖向钢筋应变均在500με以下，而端部预留孔内搭接段下端连接钢筋的应变基本达到1 500με，且搭接段上端钢筋应变小于搭接段下端钢筋应变，证明预留孔内的连接钢筋为主要受力钢筋，且400 mm的UHPC搭接段可以实现钢筋应力的有效传递。试件接近峰值点时预留孔内钢筋应变迅速上升，部分钢筋应变超过6 000με。试件被破坏时，预留圆孔底部UHPC仅产生少量裂缝，表明连接钢筋搭接区域黏结性能良好，集中配筋这一连接方式具有良好的受力性能。

图15 连接钢筋荷载-应变曲线Fig.15 Load-strain curves of connecting reinforcement

4 有限元分析

4.1 模型建立

利用有限元软件ABAQUS对试件PW1进行建模分析。模型中的混凝土部分和搭接段的UHPC均采用实体单元C3D8R，钢筋采用T3D2桁架单元。混凝土和UHPC的本构模型采用混凝土损伤塑性模型，钢筋本构模型采用简化后的“双折线模型”。采用embedded的方式将钢筋嵌入混凝土中，由于试验中连接钢筋在UHPC中锚固良好，故连接钢筋也采用embedded的方式嵌入UHPC中。建模时，将U形键槽水平接缝简化为平直接缝，预留孔孔壁和后浇混凝土、UHPC采用tie接触。

4.2 分析结果对比

4.2.1 试验结果

通过有限元分析得到的试件PW1混凝土的拉伸损伤和压缩损伤分布云图分别如图16(a)和图16(b)所示。对比图16(a)和图7(b)可知：模型的受拉损伤分布与试件PW1的裂缝分布基本吻合(模型中预留孔孔壁和后浇混凝土采用tie接触，故拉伸损伤云图中并没有交叉斜裂缝对应的损伤分布)。由图16(b)可知：混凝土压缩损伤主要集中在剪力墙两侧墙角处，墙中连接钢筋底部区域有轻微损伤，墙体其他部位未出现明显的压缩损伤。试验时，试件PW1墙角混凝土压溃严重，剪力墙预留圆孔底部区域有少量裂缝，如图16(c)和图16(d)所示。对比图16(b)～16(d)可知混凝土压缩损伤分布与试件的破坏形态基本吻合。

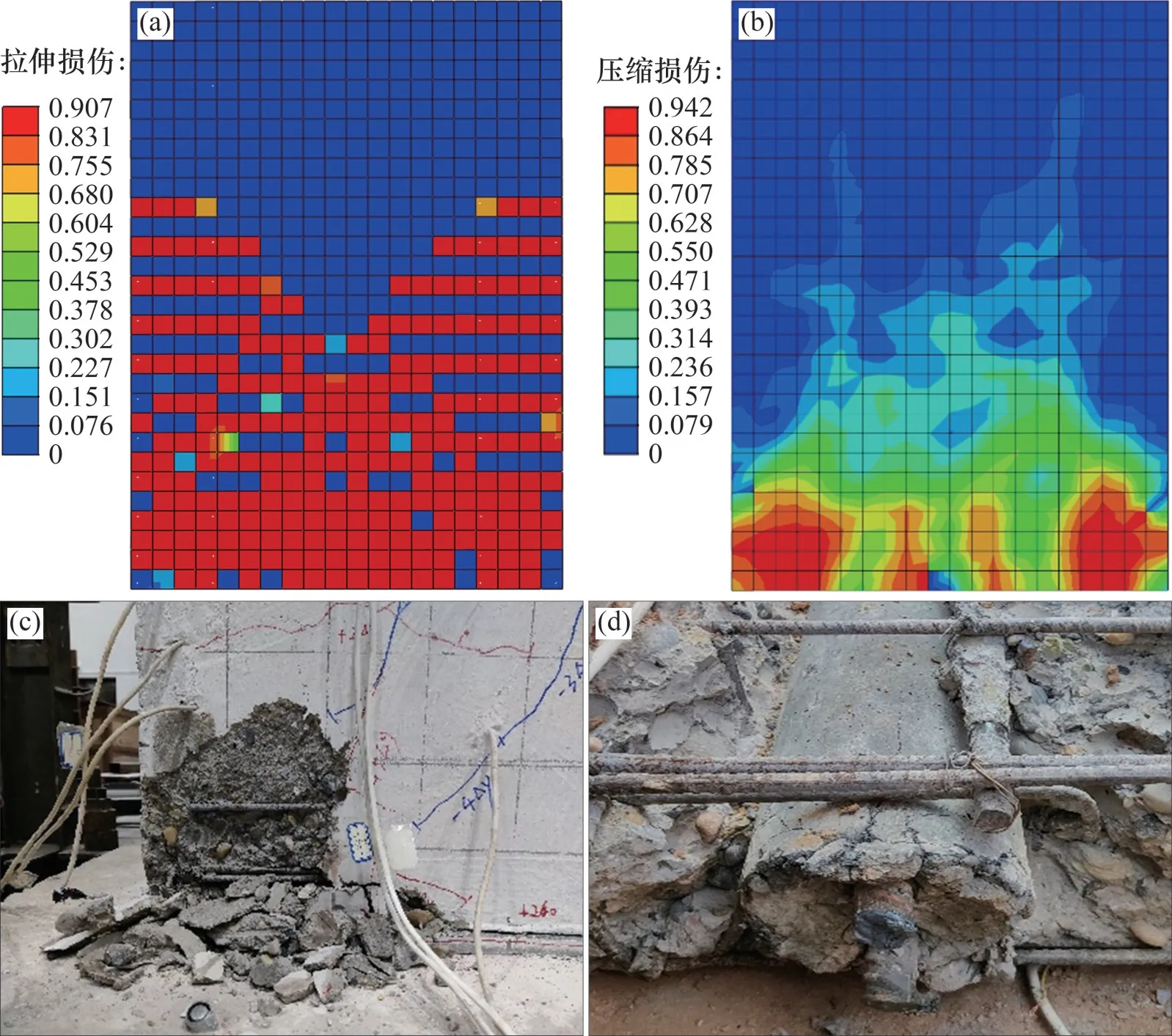
图16 试验现象对比Fig.16 Comparison of experimental phenomena

4.2.2 滞回曲线

将试验和有限元模拟得到的滞回曲线进行对比，结果如图17所示。由图17可知：有限元模拟结果与试验结果基本吻合；整体上，模拟所得滞回曲线和试验所得滞回曲线的走势基本一致，模拟得到的峰值荷载为595 kN，试验得到的峰值荷载为615 kN，两者仅相差3.4%；在加载初始阶段，模型墙体的刚度略低于试验墙体的刚度；而在位移较大时，模型墙体与试验墙体的刚度相近，这是因为模拟时将U形键槽水平接缝简化为平直接缝，且未考虑基础梁水平凹槽两端对剪力墙的约束作用。

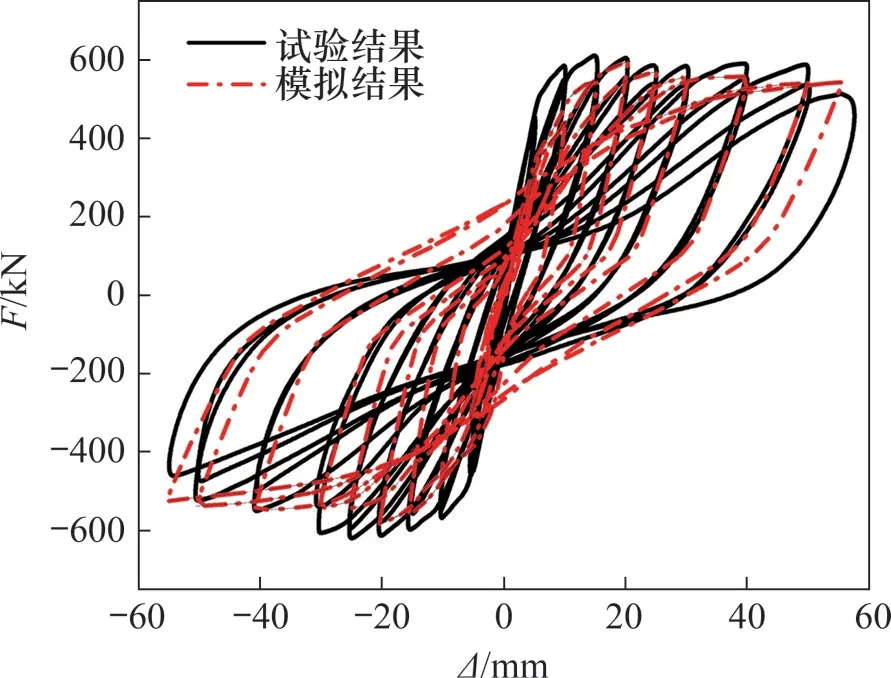
图17 试验滞回曲线和模拟滞回曲线对比Fig.17 Comparison of experimental and simulated hysteresis curves

4.3 参数分析

4.3.1 轴压比对结构刚度和承载力的影响

以试件PW1的有限元模型为基础，保持其他参数不变，分别建立轴压比为0.05～0.30的有限元模型并进行分析，得到不同轴压比下模型的滞回曲线和骨架曲线，如图18和图19(a)所示。轴压比与峰值荷载的关系曲线见图19(b)。由图18和图19可知：增大轴压比，滞回曲线所围成的面积逐渐增大，同时呈现出越来越强的捏缩特性，模型的承载力和刚度不断增加；当轴压比从0.05提升至0.10时，模型承载力和刚度的增加最显著；当轴压比从0.10提升至0.30时，承载力和刚度的增幅较小。对图19中数据进行计算可知，模型峰值荷载的增幅在轴压比为0.05～0.10时最大，为54.03 kN；当轴压比在0.10～0.30之间时，轴压比每提升0.05，承载力平均仅增加26.59 kN。

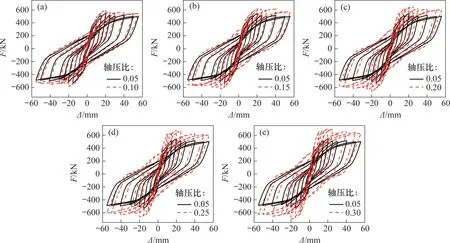
图18 不同轴压比下模型的滞回曲线Fig.18 Hysteresis curves of model for different axial pressure ratios

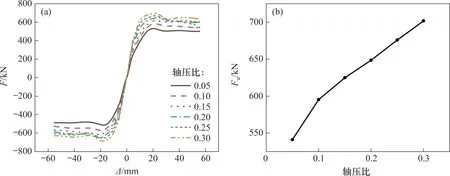
图19 不同轴压比下模型的骨架曲线和峰值荷载Fig.19 Skeleton curves and peak load of model with different coaxial-pressure ratios

4.3.2 集中配筋率对承载力、刚度、耗能和墙角抬角的影响

图20 不同集中配筋率下模型的滞回曲线Fig.20 Hysteretic curves of model with different central reinforcement ratio

图21 不同集中配筋率下模型的骨架曲线、峰值荷载和墙角抬高Fig.21 Skeleton curves, peak load and corner elevation of model with different central reinforcement ratio

5 结论

1) 集中配筋连接预制剪力墙的破坏规律与现浇剪力墙的破坏规律相同，均为弯剪破坏，且两者的抗弯承载力和抗震性能相近。在轴压比为0.10时，集中配筋连接预制剪力墙的延性系数和极限位移角均较大，远高于规范对于剪力墙弹塑性变形能力的要求。试件加载前期，试件PW3具有较好的受力性能，其开裂荷载和屈服荷载均与现浇试件SW1的相近；试件加载后期，试件PW1和PW2具有相近的峰值荷载和破坏荷载。

2) 当UHPC强度为135 MPa、钢筋搭接长度为400 mm时，UHPC能够确保预制混凝土剪力墙间接搭接段的强度；当竖缝形式为出筋搭接和U形键槽时，UHPC和高强灌浆料能够确保预制混凝土剪力墙的整体性，使用UHPC的集中配筋连接预制剪力墙具有良好的抗震性能。

3) 集中配筋连接预制剪力墙的裂缝发展没有现浇剪力墙的裂缝发展充分，但其存在独有的试验现象，即交叉斜裂缝(预留孔壁处)和水平接缝座浆层贯穿破坏，其中，水平接缝座浆层贯穿破坏后剪力墙的滑移导致预制试件滞回曲线具有更明显的捏缩特征。

4) 竖缝对预制剪力墙承载力的影响不大，但对墙体的延性和耗能能力有一定的削弱作用。2种竖缝形式的预制剪力墙均有较好的抗震性能，竖缝形式采用UHPC出筋搭接能有效抑制墙体裂缝的开展，墙体具有更好的整体性；竖向接缝采用U形键槽可提升墙体的刚度，且竖缝形式采用U形键槽的预制墙具有更好的耗能性能。

5) 试件PW1的有限元模拟结果和试验结果较吻合。当轴压比在0.05～0.30之内时，随着轴压比增加，模型的刚度和承载力不断增加，滞回曲线的捏缩程度逐渐增大；当轴压比从0.05增加到0.10时，峰值荷载的增幅达到最大；随着集中配筋率增加，模型的刚度基本不变，承载力和耗能不断增加，墙角抬高不断减小，当模型的集中配筋率保持在90%～110%时，其抗弯承载力和墙角抬高量处于最佳状态。