格栅节点加强对风积沙筋土界面力学性能的影响
2024-03-01杜炜聂如松谭永长张杰祁延录赵春彦
杜炜,聂如松,2,谭永长,张杰,祁延录,赵春彦
(1.中南大学 土木工程学院,湖南 长沙,410075;2.中南大学 重载铁路工程结构教育部重点实验室,湖南 长沙,410075;3.新疆铁道勘察设计院有限公司,新疆 乌鲁木齐,830011)
土工格栅加筋土结构因其具有良好的力学性能,广泛运用于工程实践中[1-2]。筋土界面的相互作用行为对加筋土结构稳定性有直接影响,格栅纵肋、横肋提供的摩擦阻力和被动抗阻力可有效地约束土体移动。TANG等[3-4]认为拉拔试验是研究土工格栅加筋土结构荷载传递机制和计算相关参数的较好方法。国内外研究者通过拉拔试验,对筋土相互作用特性进行了研究。LOPES等[5]研究了围压、填料密度、拉拔速度对单向土工格栅抗拔性能的影响,从拉拔试验结果发现随着围压、填料密度或拉拔速度增大,拉拔阻力增大。AHMADI等[6]制作了4种不同孔径的土工格栅,与5种不同级配曲线的道砟相互组合进行拉拔试验,发现不同级配的道砟均存在1个最优孔径,若孔径过小,则会减弱土工格栅与道砟的嵌锁作用,导致拉拔阻力降低;若孔径过大,则会减弱土工格栅与填料间的摩擦力,导致拉拔阻力下降。曹文昭等[7]开展拉拔试验,对比研究了双向土工格栅和三向土工格栅的加筋性能,发现双向土工格栅应变更加均匀,三向土工格栅的应变集中在拉拔端附近。苗晨曦等[8]对不同网孔类型土工格栅的剪切带、接触力链、细观组构、筋材轴力分布等细观特性进行了讨论,认为不同界面法向压力下应采用不同的网孔形状。王志杰等[9]研究了加载方式对筋土界面细观特性的影响,发现采用刚性顶部加载方式所得结果与柔性顶部加载方式所得结果存在明显区别。
随着研究不断深入,土工合成材料结构形式趋于三维化。张孟喜等[10]提出了立体加筋的概念,制定了多种立体加筋的方案,通过三轴压缩试验研究了加筋形式和加筋高度对砂土强度的影响。李磊等[11]将不同厚度的土工膜固定在土工格栅节点上,形成了具有立体加筋效果的加强节点土工格栅,通过开展一系列拉拔试验,研究了加强节点厚度与极限拉拔阻力增量的关系,认为在一定范围内两者呈线性关系,且横肋间距和法向应力对相关系数有影响。邱成春等[12]基于离散元法建立了二维的路堤数值模型,研究了加强节点土工格栅加筋路堤的细观特征,与无筋路堤和普通格栅加筋路堤相比,加强节点土工格栅加筋路堤的累积沉降更小,内部应力分布更均匀。张孟喜等[13]研究了节点布置方式对拉拔试验结果的影响,发现当厚度一定时,上下两侧各布置一半厚度节点的方式优于上侧布置节点的方式,但不能解释节点布置方式影响试验结果的作用机理。BEYRANVAND等[14]在土工格栅上黏附混凝土块,展开土工格栅加筋砂土的拉拔试验,通过黏附混凝土块提升了格栅的被动抗阻力。这些研究以普通土工格栅为研究对象,大多局限于宏观层面,对加强节点改善土工格栅加筋性能的细观机理尚不明确。为此,本文作者采用离散元软件PFC建立加强节点加筋风积沙拉拔试验的数值模型,研究节点布置方式影响试验结果的作用机理,证实节点群体效应的存在,得出最优的相邻节点间距;工程中常采用经验的方法铺设土工格栅,会造成一定程度的浪费,为此,对普通土工格栅与加强节点土工格栅的剪切带范围进行对比分析,评价不同加强节点厚度土工格栅的立体加筋效果,以便为加强节点土工格栅的铺设间距提供参考。
1 试验流程与参数标定
1.1 试验流程与模拟思路
开展风积沙的静三轴压缩试验,建立三轴试验数值模型,根据三轴试验结果进行参数反演,确定风积沙的细观参数。开展土工格栅的单肋条拉伸试验,建立单肋条拉伸试验的数值模型,确定土工格栅的细观参数。建立普通土工格栅加筋风积沙拉拔试验的数值模型,代入风积沙和土工格栅的参数,依据拉拔试验结果验证数值模型的合理性,在拉拔试验数值模型的基础上展开进一步研究。
1.2 风积沙细观参数标定
室内试验填料为风积沙,取自塔克拉玛干沙漠。风积沙数码照片和电镜扫描照片见图1,风积沙基本物理特性参数见表1。三轴试验在TSZ全自动三轴仪上进行,试样直径为39.1 mm,高度为80.0 mm。制样过程依据GB/T 50123—2019《土工试验方法标准》执行。研究表明[15],因风积沙强度低、黏聚力小,制样时建议不要在饱和器底部垫滤纸及四周涂抹凡士林,制样完成后立即开展试验,以避免取样时大量沙土黏在饱和器四周,造成试样不完整。试样在最优含水率状态下按压实系数K=0.93制备,在30 kPa围压下开展固结不排水静三轴压缩试验。

表1 风积沙物理特性参数Table 1 Physical parameters of aeolian sand

图1 塔克拉玛干沙漠风积沙照片Fig.1 Photos of aeolian sand in Taklamakan Desert
图2所示为三轴试验物理模型和数值模型。初始状态下数值模型中试样高度为80 mm,直径为39.1 mm。三轴数值模型尺寸与物理模型尺寸保持一致。柔性膜颗粒之间接触采用线性黏结接触模型,组成柔性膜的颗粒半径取0.64 mm,表2所示为柔性膜的细观参数,主要参考了橡胶膜的拉伸试验的参数[16],由于不考虑柔性膜破坏的情况,柔性膜采用较高的黏结强度。采用光滑球体模拟风积沙颗粒,虽然风积沙颗粒相对均匀,但仍有肉眼不可见的棱角。为了使模拟结果尽可能地与实际结果匹配,风积沙采用抗转动接触模型,考虑实际颗粒不规则形状。通过多次试算,反复改变颗粒变形模量、摩擦因数及相关颗粒参数,直到模拟结果与试验结果相近。最终选取具有42 159个颗粒的试样,该数量足以反映材料特性。风积沙之间的接触以及风积沙与土工格栅的接触均采用表3中参数。图3所示为三轴试验标定结果(围压为30 kPa),从图3可见:体应变-轴向应变在加载初期较接近,随着轴向应变增大,模拟结果与试验结果差别变大,偏应力-轴向应变曲线整体的发展趋势基本相同,误差较小。

表2 膜颗粒接触模型细观参数Table 2 Mesoscopic parameters of flexible films

表3 风积沙标定参数Table 3 Calibration parameters of aeolian sand

图2 三轴物理模型及其颗粒流模拟Fig.2 Physical model of triaxial test and particle flow simulation

图3 偏应力-轴向应变和体应变-轴向应变曲线Fig.3 Deviatoric stress-axial strain and volume strainaxial strain relationship curves
1.3 土工格栅参数标定
本试验所用格栅为双向土工格栅,如图4(a)所示。采用单肋法测试,试样在仪器上的标距为235 mm,拉伸速度为50 mm/min,在横肋、纵肋各取5个试样。试验严格按照国家标准规定的步骤进行。格栅尺寸和单肋条拉伸试验测得的宏观力学参数见表4。如图4(b)所示,编号1~7代表埋置在有效区域的7条横肋。格栅颗粒间采用平行黏结接触模型,平行黏结接触模型受拉不受压,能较好地模拟土工格栅拉伸强度高的特点。模拟土工格栅采用的细观参数见表5。普通土工格栅实测与计算的拉伸强度-应变关系曲线见图5,从图5可见应力计算结果与实测结果较吻合。

表4 土工格栅尺寸及力学参数Table 4 Geogrid dimensions and mechanical parameters
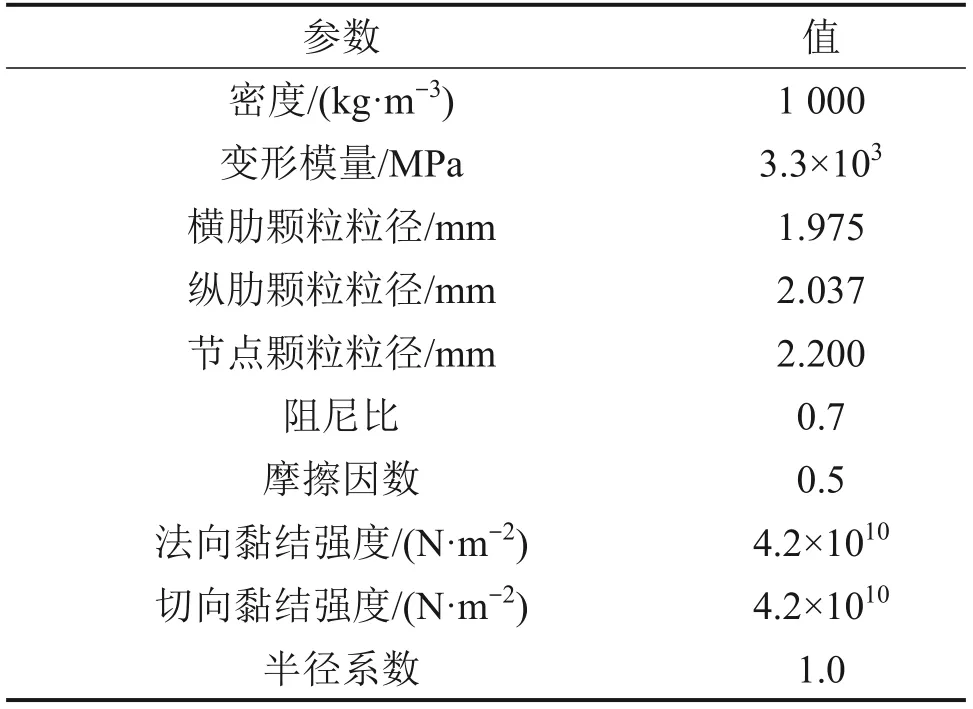
表5 土工格栅细观参数Table 5 Meso-parameters of geogrid

图4 土工格栅图Fig.4 Drawing of geogrid

图5 土工格栅的拉伸强度-应变关系对比Fig.5 Comparison of tensile strength-strain relationship of geogrid
2 拉拔试验及其数值模型
2.1 室内拉拔试验
图6所示为YT1200S型直剪拉拔摩擦仪,试验箱长×宽×高为250 mm×200 mm×200 mm。试验填土共分4次填入压平,每层填土高度为50 mm。土工格栅为不具有加强节点的普通格栅,土工格栅长度取280 mm,在土体中的长度为250 mm,剩余30 mm预留长度的格栅用于与夹具连接。土工格栅的宽度为150 mm,与试验箱两侧各保持25 mm距离。填入2层土样并找平,安装土工格栅。安装时,在拉拔出口涂抹润滑剂以免造成卡口影响试样结果。然后,继续分层填筑至试验箱顶面,此时,填土高度为200 mm。将刚性荷载板置于已填筑好的试样土体顶面,施加法向压力,持续维持法向压力15 min,使风积沙-土工格栅紧密接触,再进行拉拔试验。考虑到土工格栅埋置在路基不同深度位置,据文献[17],拉拔试验法向压力确定为15、30和60 kPa,拉拔速度为0.5 mm/min,当拉拔端位移达15 mm时终止试验。对同一类土样、同一法向压力下的试样进行5组平行试验,通过综合比较以降低试验结果的离散性。

图6 直剪拉拔摩擦仪Fig.6 Pull-out test apparatus
2.2 拉拔试验数值模型
拉拔试验数值模型与物理试验几何尺寸一致。受计算机算力的限制,模拟颗粒往往要放大数十倍,以提高计算效率。但这种方法明显降低了计算精度,且已有研究证明[18]:当放大倍数过高时,模拟颗粒体积较大,其沿筋材转动和滑动,在拉拔过程中不断形成密实的颗粒排列状态,导致出现峰后拉拔力大幅度波动的情况。为研究放大倍数的影响,参考文献[19],构建分层风积沙数值模型,越接近土工格栅,放大倍数越小,将算力集中于筋土核心区域并构建均质风积沙数值模型。采用颗粒排斥法生成土样,颗粒级配假定呈线性分布。图7(a)所示为生成分层风积沙数值模型,将风积沙分为5层,颗粒数量为64 425个。图7(b)所示为均质风积沙数值模型,颗粒粒径分布范围为4.5~7.5 mm,中值粒径d50为5.98 mm,颗粒数量为50 041个。模拟颗粒与现实风积沙的级配曲线如图8所示。从图8可见:在分层风积沙数值模型中,筋土界面附近的风积沙颗粒放大倍数最小,颗粒粒径分布范围为1.6~5.2 mm,中值粒径d50为3.4 mm,厚度为35 mm;第2层和第4层的颗粒粒径分布范围为5.7~7.5 mm,厚度为35 mm;第1层和第5层的颗粒粒径分布范围为6.75~11.25 mm,厚度约为80 mm。理论研究表明,只要选取尺度相关的微观本构,放大粒径试样与原粒径试样便具有相同的力学响应,但应保证三维模拟单元试验颗粒数目大于40 000个[20],且颗粒集合体外观直径与内部颗粒平均粒径的比值在计算能力允许的情况下应尽可能地大,但不应小于30[21]。利用Fish函数赋予拉拔端固定水平速度,MIAO等[22-23]取拉拔速度为0.375 m/s。经多次试算,当拉拔速度小于1 m/s时,拉拔位移-拉拔力曲线趋于稳定。本文取拉拔速度为0.2 m/s,将土工格栅拔出15 mm时终止计算。记录拉拔力、拉拔位移、孔隙率、格栅应变的变化,在拉拔过程中,每100 s步记录1次参量。

图7 风积沙数值模型Fig.7 Numerical models of aeolian sand

图8 模拟颗粒与现实风积沙的级配曲线Fig.8 Gradation curves of simulated particle and aeolian sand
2.3 数值模型的验证
图9所示为分层风积沙数值模型、均质风积沙数值模型和室内试验的拉拔阻力与位移的关系曲线。从图9可见:总体上看,试验初期曲线近似呈线性增大;随着拉拔端位移增大,拉拔力的增速逐渐降低;到达峰值后,数值模拟结果呈现出小幅度的波动下降趋势;随着法向压力增大,曲线整体升高,与峰值所对应的拉拔位移也越大;在同一法向压力下,模拟曲线与试验曲线较接近,发展规律相似,拟合度较高,证明分层风积沙数值模型和均质风积沙数值模型的合理性;当法向压力为15 kPa和30 kPa时,均质风积沙数值模型的拉拔力-拉拔位移曲线整体略高于分层风积沙数值模型曲线;当法向压力为60 kPa时,均质风积沙数值模型的拉拔力明显偏高,均质风积沙模型的拉拔端附近存在粒径较大的颗粒,导致格栅在拉拔过程中容易卡口,刚性前壁附近的应力集中现象更显著。整体上看,与均质风积沙数值模型相比,分层风积沙数值模型结果更接近于室内试验结果,证明了分层风积沙数值模型的优越性。
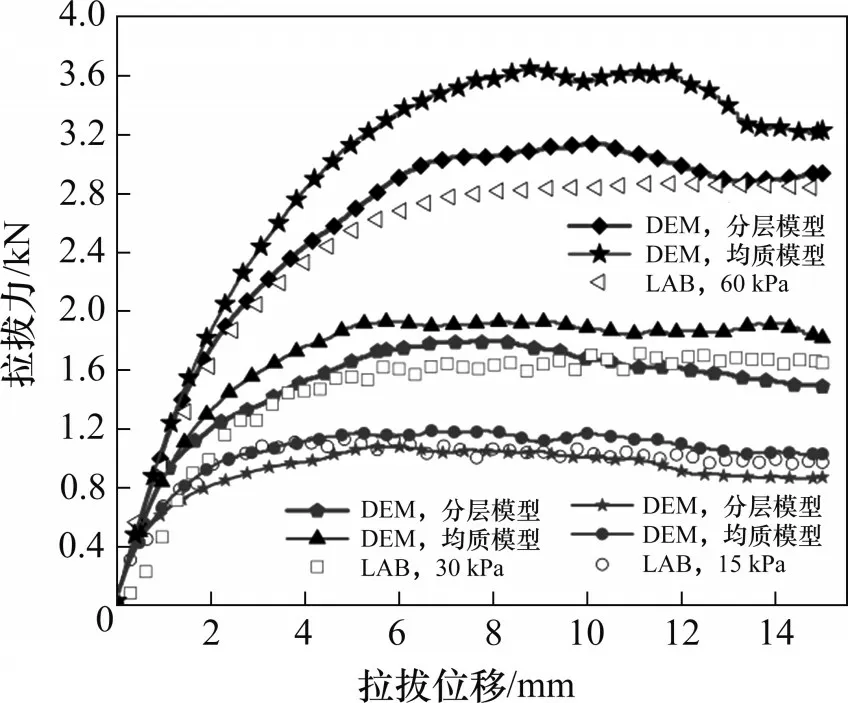
图9 拉拔力与拉拔位移的关系Fig.9 Relation between pull-out force and pull-out displacement
2.4 加强节点及计算工况
为研究节点排布方式对筋土界面的力学影响,共考虑3种型式:格栅节点上、下两侧分别加强和两侧同时加强。不同节点布置方式如图10所示。格栅节点加强工况见表6。

表6 试验工况Table 6 Test cases

图10 不同节点布置方式Fig.10 Different node arrangements
3 计算结果分析
3.1 节点加强方式对极限抗拔阻力的影响
不同法向压力和节点布置方式下的拉拔阻力与位移的关系见图11。从图11可知,加强节点显著提高了土工格栅的极限拉拔阻力;以30 kPa法向压力的工况为例,普通土工格栅的极限拉拔阻力为1 800 N,工况B的极限拉拔阻力为1 910 N,相比于普通格栅提高了6.11%。工况D的极限拉拔阻力为1 930 N,相比于普通格栅提高了7.22%;工况C的极限拉拔阻力为1 960 N,相比于普通格栅提高了8.89%;当材料用量一定时,与工况B和D相比,工况C中土工格栅的极限拉拔阻力增幅最大,不同的法向压力下均呈现出类似的规律。

图11 不同节点布置方式下拉拔阻力与位移的关系Fig.11 Relationship between pull-out force and pull-out displacement in different node layouts
JEWELL等[24]提出了经典的刺入剪切破坏模式,ALAGIYAWANNA等[25]发现拉拔阻力的刺入剪切理论值与试验值在低法向压力下较接近,法向压力较高时差异较大。设σb为横肋的承载应力,其计算式如下:
式中:σ'n为土工格栅受到的法向压力,包括加载板施加的恒定法向压力与上覆风积沙重力产生的法向压力;φ为风积沙的内摩擦角(rad)。计算得到σb的具体值后,加强节点提供的极限拉拔阻力增量T可依据下式[13]计算:
式中:H为加强节点的厚度;W为加强节点的宽度;N为节点的数量。基于刺入剪切破坏理论,极限拉拔阻力增量理论解与数值解的对比见图12。从图12可见:当法向压力为15 kPa和30 kPa时,理论解与数值解的差异较小;当法向压力为60 kPa时,工况B的极限拉拔阻力增量数值解较接近理论解,工况C的结果偏大,工况D的结果偏小。总体上看,不同工况下的极限拉拔阻力增量数值解与理论解较接近,证明图10中模拟节点方法是合理的。
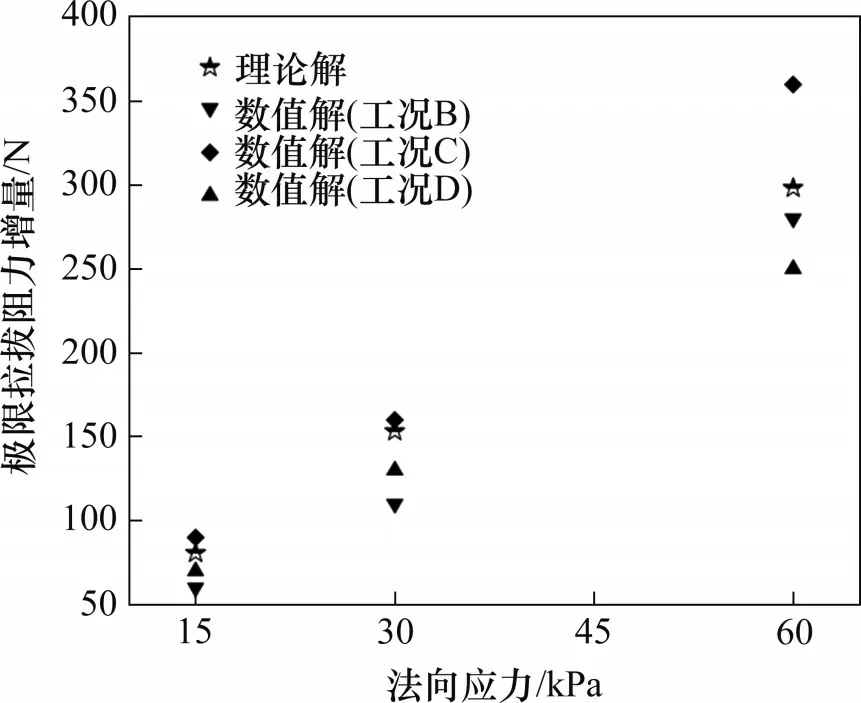
图12 极限拉拔阻力增量数值解与理论解对比Fig.12 Comparison of numerical and theoretical solutions for increment of ultimate pull-out resistance
3.2 节点加强方式对筋土界面强度参数的影响
剪切强度-法向压力拟合曲线见图13。基于静力平衡和筋土界面剪应力均匀分布假设,依据
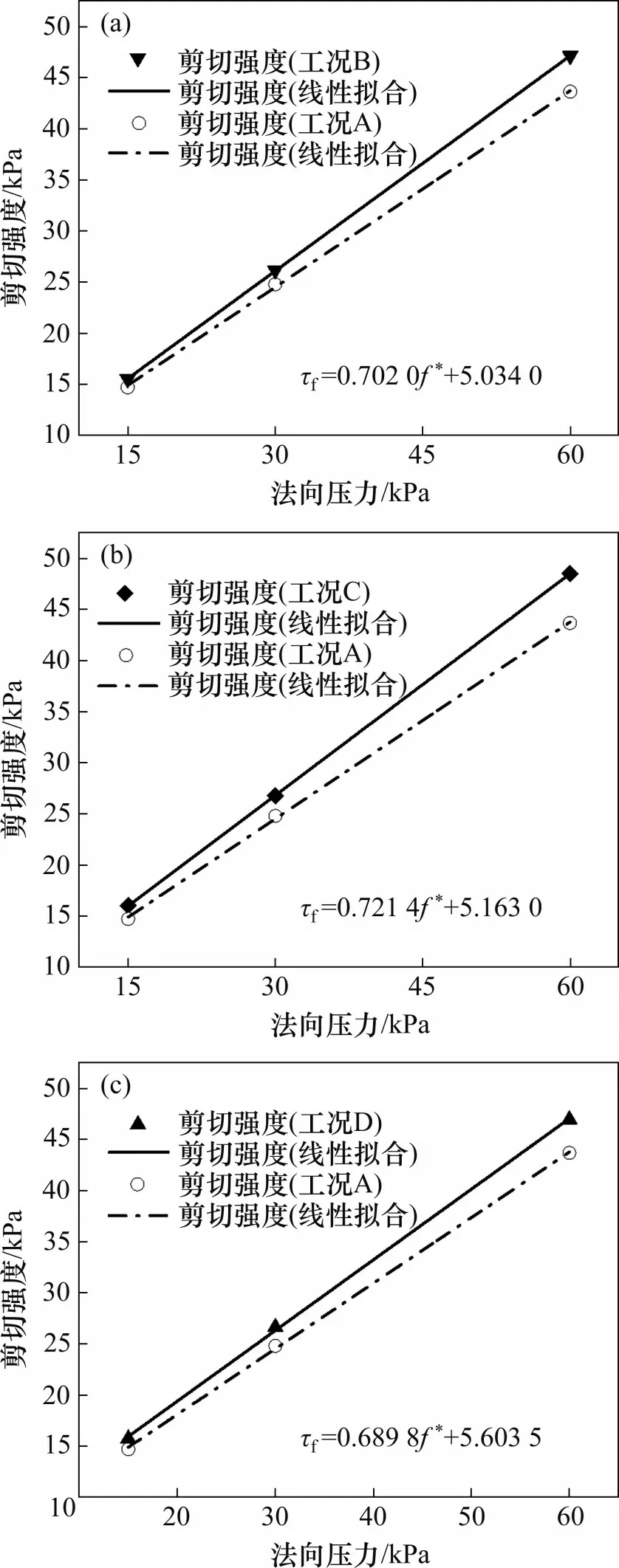
图13 剪切强度-法向压力拟合曲线Fig.13 Shear strength-normal pressure fitting curves
对界面剪切强度与法向压力关系进行线性拟合,反算界面强度指标。式(3)中,τf为界面剪切摩擦强度;σn为法向应力,f*为似摩擦因数,Csg为似黏聚力。不同节点布置方式下的界面摩擦强度参数如表7所示。从表7可以看出:普通格栅和加强节点格栅的似黏聚力变化很小,在5.1~5.6 kPa之间波动,因而,节点加强对似黏聚力的影响很小,可以忽略不计。节点加强后,界面摩擦角增大2°~3°;当节点上下两侧同时加厚时,界面摩擦角的增幅最大。
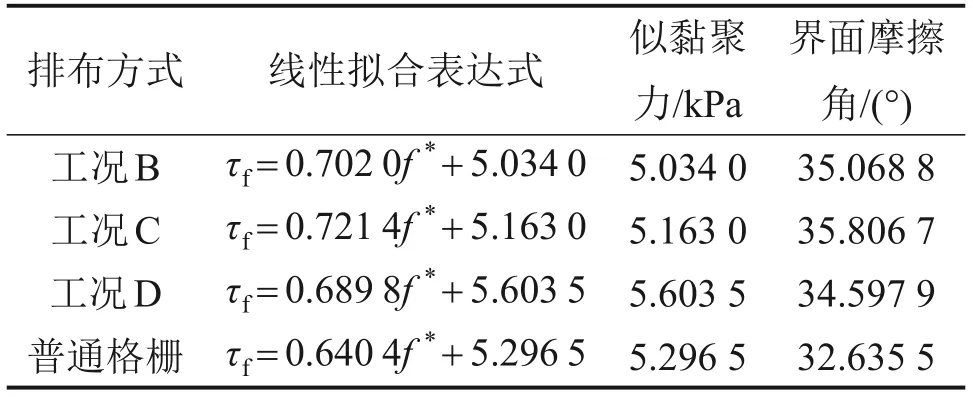
表7 不同节点布置方式下的界面摩擦强度参数Table 7 Interface strength parameters under under different node arrangements
3.3 加强节点厚度对极限抗拔阻力的影响
不同加强节点厚度下的拉拔力-拉拔位移曲线关系见图14(法向压力为30 kPa)。工况C中土工格栅的极限拉拔阻力为1 960 N,相比于普通格栅(工况A)峰值提高8.89%,单位厚度加强节点对峰值的提高率为2.02%。工况E中土工格栅的极限拉拔阻力为2 130 N,峰值提高18.33%,单位厚度节点对峰值的提高率为2.08%。工况F中土工格栅的极限拉拔阻力为2 260 N,峰值提高了25.56%,单位厚度节点对峰值的提高率为1.94%。工况G中土工格栅的极限拉拔阻力为2 430 N,峰值提高了35.00%,单位厚度节点对峰值的提高率为1.99%;当节点厚度变大时,节点提供的极限拉拔阻力增量增大,单位厚度节点对峰值的提高率变化不大。节点增厚厚度与极限拉拔阻力增量的关系曲线见图15,其中,T为极限拉拔阻力增量,H为节点增厚厚度,节点增厚厚度指上侧加厚厚度与下侧加厚厚度之和。从图15可以看出:节点增厚厚度H与极限拉拔阻力增量具有良好的线性关系。

图14 不同加强节点厚度下的拉拔力-拉拔位移曲线Fig.14 Pull-out force versus pull-out displacement curves of different thicknesses of strengthened nodes

图15 节点增厚厚度与极限拉拔阻力增量的关系Fig.15 Relationship between node thickness and ultimate pull-out resistance increment
3.4 加强节点厚度对格栅应变的影响
沿拉拔方向,土工格栅的应变情况差异很大,有必要将土工格栅分为前、中、后3段(见图4(b)),每段长度约为93.3 mm。不同节点厚度土工格栅的应变变化规律(法向压力为30 kPa)见图16。从图16可见:总体上看,不同工况下格栅前段的应变最大,格栅中段的应变其次,格栅后段的应变最小;格栅前段应变的曲线形状最接近拉拔力-拉拔位移曲线的形状,说明格栅前段承担了较多的拉拔阻力。不同加强节点厚度土工格栅的分段峰值应变如表8所示。从表8可见:与普通格栅(工况A)相比,工况C格栅前、中、后段的峰值应变分别增大了10.45%、9.15%、14.67%;工况E格栅前、中、后段的峰值应变分别增大了21.64%、22.00%、18.67%;工况F格栅前、中、后段的峰值应变分别增大了33.13%、23.53%、40.89%;工况G格栅前、中、后段的峰值应变分别增大了46.72%、37.25%、45.78%。加强节点显著提高了格栅每段的应变率,更充分地利用了格栅的加筋性能,且加强节点的厚度越大,格栅每段的应变峰值越大。分段峰值应变增量与节点增厚厚度关系曲线见图17,可见格栅分段峰值应变与节点增厚厚度有良好的线性关系。由线性拟合表达式斜率可知,格栅前段的峰值应变增长速度为格栅中段的1.81倍,是格栅后段增长速度的2.83倍。说明节点厚度增量对格栅前段的影响更强烈,越靠近拉拔端,节点厚度增量的影响越显著。

表8 不同工况土工格栅的分段峰值应变Table 8 Sectional peak strain of geogrid under different conditions

图16 不同节点厚度土工格栅的应变变化规律Fig.16 Strain variation laws of geogrids with different node thicknesses
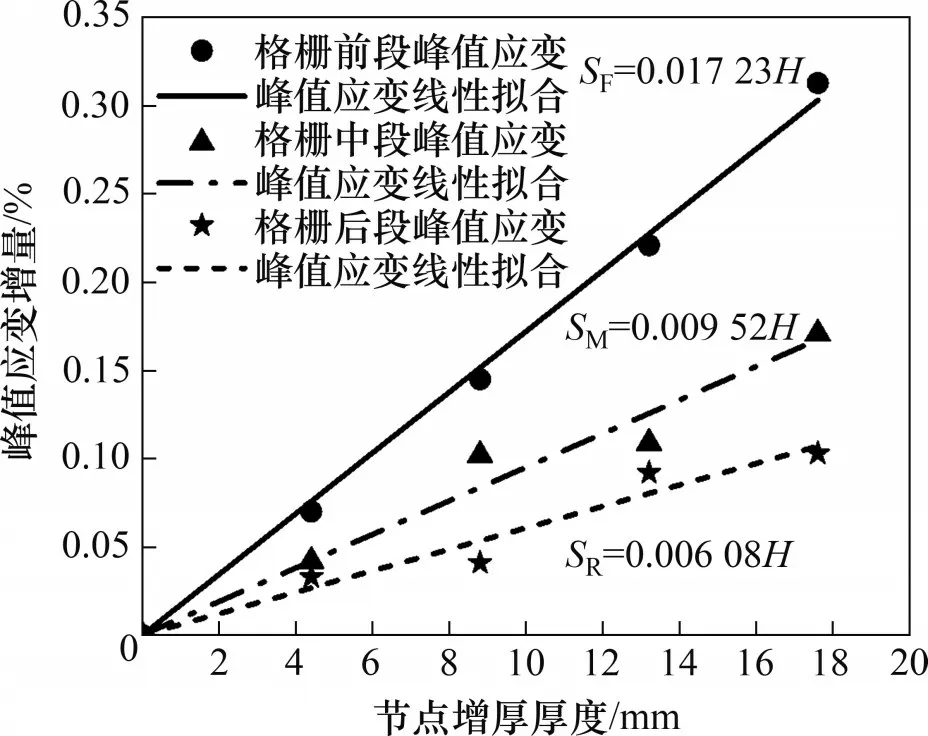
图17 峰值应变增量与节点厚度增量关系曲线Fig.17 Curves of relationship between peak strain increment and node thickness increment
3.5 加强节点厚度对筋土界面孔隙率的影响
在筋土界面布置55个直径为2.5 cm的测量球,通过测量球可测得筋土界面孔隙率的变化规律,如图18所示。拉拔前后筋土界面处局部孔隙率和试样体积的变化情况见表9。从图18和表9可见:拉拔结束后,对于普通土工格栅的工况,筋土界面的孔隙率上升7.82%,风积沙试样体积上升了0.28%;工况C中筋土界面的孔隙率上升了9.09%,试样体积上升了0.48%,体积变化率为普通格栅的1.74倍;工况E中筋土界面的孔隙率上升了10.04%,试样体积上升了0.58%,体积变化率为普通格栅的2.08倍;工况F中筋土界面的孔隙率上升了9.33%,试样体积上升了0.57%,体积变化率为普通格栅的2.06倍;工况G中筋土界面的孔隙率上升了9.30%,试样体积上升了0.70%,体积变化率为普通格栅的2.50倍。与普通土工格栅相比,加强节点土工格栅对界面处风积沙的扰动更强烈,试样整体的剪胀趋势更加显著。

表9 筋土界面处局部孔隙率和试样体积变化Table 9 Local porosity and sample volume change at interface between reinforcement and soil

图18 测量球布置位置Fig.18 Measuring ball arrangement position
3.6 加强节点厚度对接触力链的影响
将接触力链按比例显示,投影到XOZ平面上,得出2种工况拉拔结束后的力链分布情况,如图19所示。从图19可见:工况A和工况G表现的整体分布规律相似,刚性后壁附近存在明显的应力空洞,刚性前壁附近则存在应力集中现象,且越靠近前壁,应力集中现象越明显。力链在横肋附近表现为锯齿状分布。与工况A相比,工况G在拉拔端附近的应力集中现象更加显著,说明工况G的土工格栅对风积沙的影响程度更大。
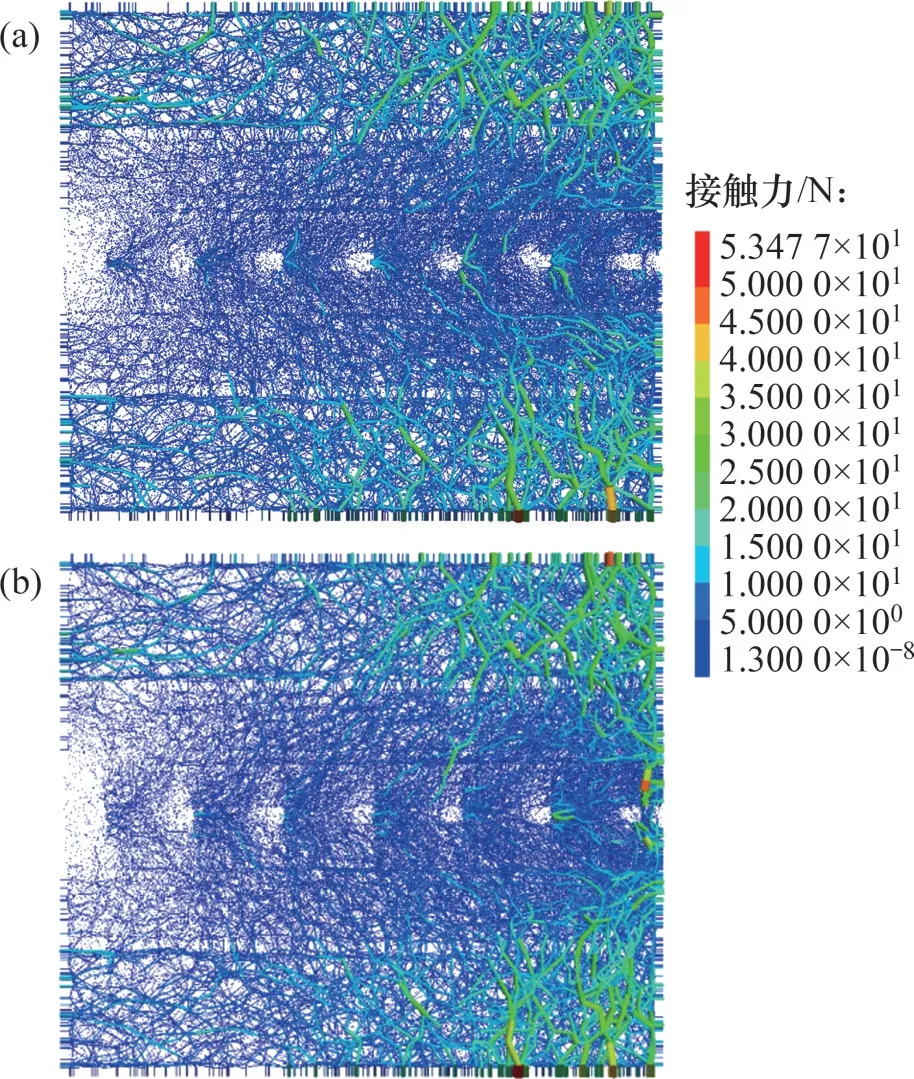
图19 2种工况下的力链分布Fig.19 Force chain distribution in two conditions
3.7 加强节点厚度对剪切带范围的影响
普通格栅和工况G的格栅拔出15 mm时(法向压力为30 kPa)的风积沙颗粒位移矢量图见图20。从图20可见:总体上看,格栅前段附近的剪切带厚度比双格栅后段附近的剪切带厚度略大;在剪切带范围外,风积沙颗粒在格栅前段的运动更加剧烈,格栅后段附近颗粒受到的影响较小。对比图20(a)和(b)可知:工况G的剪切带范围比普通格栅的剪切带范围略大,且在剪切带范围外的颗粒运动更加剧烈。

图20 风积沙颗粒位移矢量图Fig.20 Displacement vectors of aeolian sand particles
以上仅对2种工况风积沙颗粒的位移情况进行了简单的定性分析,不能评价多种工况下格栅的立体加筋效果。对不同高度层次风积沙的水平位移均值进行统计,以定量分析不同厚度加强节点对剪切带范围的影响见图21,其中,每层统计高度为10 mm。由图21可知:当离开筋土界面一定范围时,风积沙颗粒水平位移均值为负值,说明这些层次的大多数颗粒往后运动。不同工况下剪切带的范围和最大水平位移均值见表10。以1 mm的水平位移均值为界,土工格栅拔出15 mm后,工况A、C、E、F、G的剪切带整体厚度分别为36.36、39.37、41.35、44.59和47.67 mm。相比于普通格栅,工况C、E、F、G的4种加强节点格栅的剪切带范围分别拓宽为原来的1.08、1.14、1.23、1.31倍,最大水平位移均值增大为原来的1.16、1.27、1.35、1.44倍。这说明加强节点一方面拓宽了剪切带的影响范围,使格栅具有立体加筋的效果,另一方面加强了格栅限制土体移动的能力。随着节点厚度增大,剪切带的分布范围越大,最大水平位移均值增大。
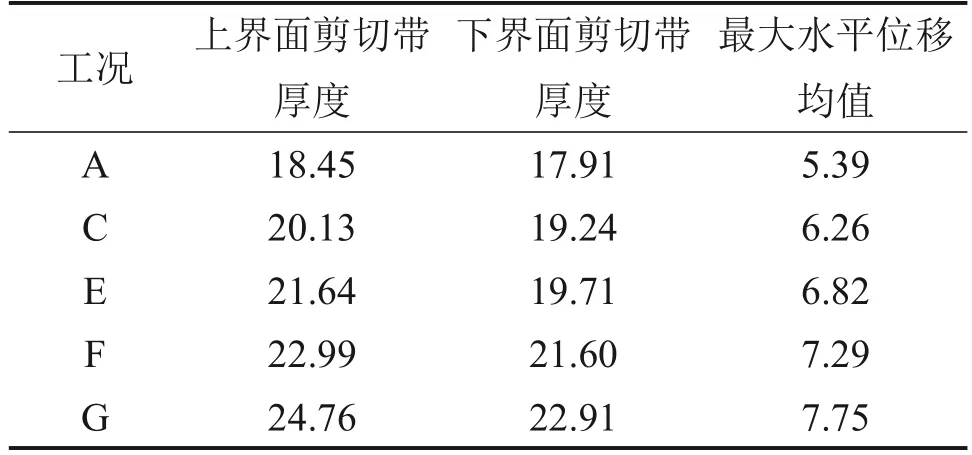
表10 不同工况下剪切带的厚度范围和最大水平位移均值Table 10 Thickness range and the maximum horizontal displacement of shear bands under different conditions mm

图21 不同高度位置颗粒的水平位移均值Fig.21 Average horizontal displacement of particles at different heights
3.8 节点群体效应
为探究节点数量与极限拉拔阻力增量的关系(法向压力为30 kPa),以工况C加强节点土工格栅为基准,随机删除加强节点,改变加强节点的数量,得到图22,图中红色圆代表加强节点。随机分布下不同加强节点数量的拉拔力-拉拔位移曲线见图23。从图23可以看出:当加强节点随机分布时,加强节点数量越多,前期拉拔力-拉拔位移曲线的斜率越大,节点提供的极限拉拔阻力增量越大。同样以工况C的加强节点土工格栅为基准,只保留某一排加强节点,节点数量固定为10个。假定横肋上的加强节点互相不影响,在这种规则分布下,每个节点可视为单独工作。在30 kPa法向压力下得到多组拉拔结果,如表11所示。表11中的7条横肋均埋在有效区域内,具体可见图4(b)。加强节点提供的极限拉拔阻力增量最小值为31.6 N,最大值为60.9 N。不同空间位置的加强节点所提供的极限拉拔阻力增量不同,说明筋土界面的剪应力分布不均匀。

表11 规则分布下节点的极限拉拔阻力增量Table 11 Ultimate pull-out resistance increment of nodes under regular distribution

图23 随机分布下不同加强节点数量的拉拔结果Fig.23 Pull-out results with different numbers of strengthened nodes under random distribution
不同分布情况下节点数量-极限拉拔阻力增量的关系见图24。从图24可见:在随机分布下,节点数量与极限拉拔阻力增量表现出良好的线性关系,得出线性拟合式T=1.961 0N(其中,T为极限拉拔阻力增量,N为加强节点数量),拟合优度为0.991 7。依据表11中数据,将每排加强节点提供的极限拉拔阻力增量相加,可得到图24中节点规则分布时的节点数量-极限拉拔阻力增量的关系。曲线采用线性拟合,T=4.464 9N,拟合优度为0.998 5。可以看出,在节点数量相同时,节点规则分布时的极限拉拔阻力增量之和大于随机分布时的极限拉拔阻力增量,证明多个节点同时工作时存在一种群体效应,导致单位数量节点对极限拉拔阻力的提高率降低。2个节点的滑裂面示意图如图25所示,纵肋上2个相邻节点的影响区域相互重叠,导致2个节点同时存在时的影响区域面积小于节点单独存在时影响区域面积之和,产生了显著的群体效应,单位数量节点对极限拉拔阻力的提高率降低。节点群体效应解释了图11所示的规律,当材料一定时,相比于单侧布置节点,上下两侧同时加强的方式,减小了重叠区域占影响区域的比例,在一定程度上减弱了节点的群体效应。

图24 节点数量-极限拉拔阻力增量的关系Fig.24 Relationship between number of nodes and ultimate pull-out resistance increment

图25 2个节点的滑裂面示意图Fig.25 Diagram of slip fracture surface of two nodes
当2个相邻节点的间距太小时,这2个节点的影响区域互相重叠,产生显著的群体效应。若增大相邻节点间距,则会存在一个临界点,使相邻节点互不影响。不同节点间距的4种设计工况见图26。节点群体效应折减系数η为评价群体效应强弱程度的量化指标,可通过下式计算:

图26 不同节点间距的设计工况Fig.26 Design conditions of different node spacings
式中:tr为节点任意分布时单位数量节点提供的极限拉拔阻力增量;ts为节点单独存在时提供的极限拉拔阻力增量。不同工况下的群体效应折减系数见表12,群体效应折减系数与相邻节点间距的关系见图27。由图27可知:随着节点间距增大,相邻节点重叠的影响区域变小,群体效应折减系数逐渐减小,节点的群体效应减弱。对群体效应折减系数进行多项式拟合,得出拟合式如下:
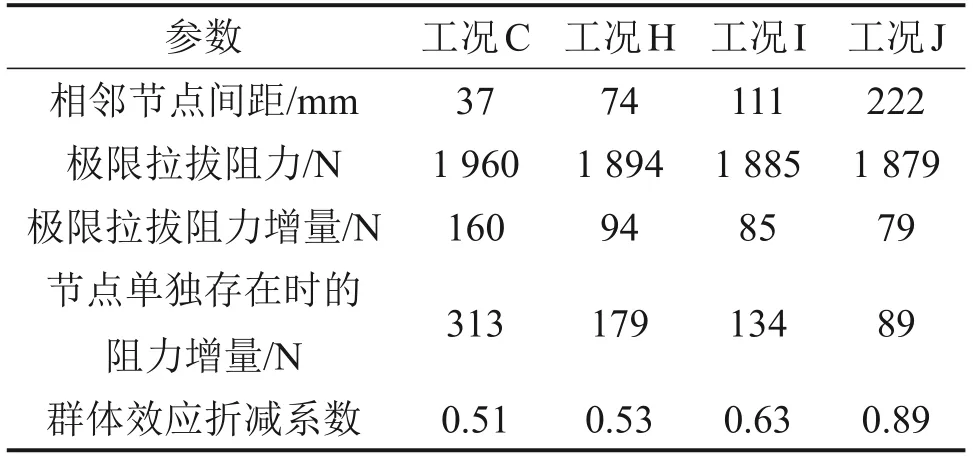
表12 不同工况下的群体效应折减系数Table 12 Reduction coefficient of group effect under different conditions
拟合优度为0.975 0,依据多项式拟合式可以预测最优的节点间距。当η为1时,得出相邻节点间距为255 mm,说明当相邻节点间距超过255 mm时,相邻节点的影响范围不再重叠,多节点同时存在时提供的极限拉拔阻力增量不会折减。
4 结论
1) 相比于均质风积沙数值模型,分层风积沙数值模型的模拟结果与室内试验结果更接近,证明了分层风积沙数值模型计算拉拔阻力的合理性及优越性。依据刺入剪切理论计算节点得到的极限拉拔阻力增量与数值解接近,证明了节点模拟方法的合理性。
2) 当多个节点同时工作时,若相邻节点间距太小,则节点的影响区相互重叠,产生节点群体效应,导致每个节点的效率降低。随着相邻节点间距增大,节点群体效应逐渐减弱。
3) 节点排布方式影响了格栅加筋性能。当节点厚度一定时,相比于单侧布置节点,双侧布置节点的方式减小了重叠区域占影响区域的比例,削弱了节点群体效应。
4) 当布置方式固定时,随节点厚度变大,节点提供的极限拉拔阻力增量变大。单位厚度节点提供的极限拉拔阻力基本不变,极限拉拔阻力增量与节点厚度增量呈良好的线性关系。
5) 格栅前段、中段、后段的峰值应变增量与节点厚度增量呈良好的线性关系,格栅前段峰值应变的增长速度为格栅中段的1.81倍,为格栅后段的2.83倍。
6) 与普通土工格栅相比,加强节点土工格栅对筋土界面的扰动更强烈,使试样整体的剪胀趋势更加显著。相比于普通土工格栅,工况G中剪切带的厚度拓宽为原来的1.31倍,发挥出明显的立体加筋效果,最大水平位移均值增大为原来的1.44倍,其具有更强的限制土体位移的能力。
