考虑黏土蠕变特性的大埋深盾构复推总推力增量解析解研究
2024-03-01王树英钟嘉政付循伟龚振宇
王树英,钟嘉政,付循伟,龚振宇
(1.中南大学 土木工程学院,湖南 长沙,410075;2.中南大学 隧地工程研究中心,湖南 长沙,410075;3.中南大学 轨道交通工程结构防灾减灾湖南省重点实验室,湖南 长沙,410075;4.中国土木工程集团有限公司,北京,100038;5.中铁五局集团电务工程有限责任公司,湖南 长沙,410205)
土压平衡盾构具有机械化程度高、对地层扰动小、占用地面空间少、掘进效率高等优点,被广泛应用于城市轨道交通、水工隧洞、综合管廊等地下工程建设项目中[1-2]。随着盾构隧道项目从小埋深、短距离掘进向大埋深、长距离掘进发展,盾构施工更容易发生刀盘“结泥饼”[3]、刀具严重磨损[4]、螺旋输送机喷涌[5]等风险。施工风险频发和盾构设备故障迫使盾构非正常停机,然后进行开仓检查、泥饼处理、刀具更换或突发喷涌处治等[6-7]。此外,长距离掘进还会面临排出渣土和物料运输效率低等问题,导致停机时间延长[8]。非正常停机时间短需数小时,长需数天甚至1月以上。研究者致力于掘进过程中的风险防控技术研究,以避免长时间停机问题[9]。长时间停机会诱发一系列次生风险,如地表沉降过大[10-11]、TBM(岩石掘进机)卡机[12]、盾构复推时推力增量较大[13]等。关于停机引起的地表沉降研究,张炜[14]根据分层总和法、Peck公式及太沙基一维固结沉降理论,通过条形均布荷载地基模型建立地表沉降与盾构停机时间的理论关系式;郭幪[15]对比了地表沉降的Mindlin理论解和数值模拟结果,发现超孔隙水压力消散、地层损失是停机期间出现地表沉降的主要原因。为了控制临时停机造成的地表沉降,章邦超等[16]提出了洞内超前注浆和克泥效工法并检验其应用效果,发现随着隧道埋深逐渐增大,长时间停机后盾构卡机或推力过大的概率增大[17]。BILGIN等[18]通过TBM工程案例分析,发现停机时间延长使掘进推力显著增加,并提出在盾壳外注射膨润土可有效缓解卡机问题。HOME[19]依托TBM卡机实例发现使用聚氨酯树脂对掘进机前方和上方的地层加固,可保证掘进机顺利重启。然而,由于软岩或黏土地层自身具有蠕变特性[20],在停机过程中,盾壳受变形软岩或土层挤压后的接触力随时间增大,进而盾构恢复推进需克服更大的盾壳-地层界面摩阻力,导致该地层出现更严重的盾构推力过大或卡机问题[21],因此,需对考虑地层蠕变效应的地层-盾壳相互作用力进行计算。近年来,一些研究者对盾壳-蠕变地层接触应力和盾构推力的计算问题进行了研究,如:BARLA等[22]将地层视为黏弹塑性体,地层模拟参数源自室内原岩蠕变试验结果,建立了TBM盾壳-地层相互作用轴对称二维数值模型,以评估盾构推力;金慧等[23]以超深埋隧道为背景,基于黏弹性理论和叠加原理,构建了考虑初始构造应力的二向等压边界下盾构-黏土地层相互作用平面应变理论模型,提出了盾壳-地层界面接触应力解析解计算方法,分析了土的黏性系数、掘进速度和停机时间对界面接触应力的影响规律。然而,针对盾构在大埋深黏土地层中的停机复推难题,目前尚未发现考虑上覆土自重应力影响的盾壳-地层接触应力和复推推力增量计算的理论研究。长时间停机会导致复推推力增量过大,将不利于盾构姿态和管片拼装质量控制。为此,本文提出盾构在大埋深黏土地层中停机后复推总推力增量的理论计算方法,假设黏土地层偏应力-应变行为服从Burgers蠕变模型,基于考虑自重的黏土地层圆截面隧洞简化力学模型,推导盾壳-地层径向接触应力黏弹性解析解,进一步采用该解析解计算盾构停机复推的总推力增量。然后,依托滇中引水工程昆明段盾构隧洞工程,通过与现场实际监测结果对比,验证总推力增量计算公式的合理性。最后,对总推力增量进行敏感性分析,提出大埋深黏土地层次生风险控制措施。
1 盾壳-地层径向接触应力黏弹性解
1.1 黏土地层圆截面盾构隧洞简化力学模型
1.1.1 基本假定
为了建立考虑地层应力的大埋深圆截面盾构隧洞开挖卸载力学模型并求得洞周围岩应力与位移的解析解,进行以下假设:
1) 隧洞开挖影响范围内地层是均匀、连续、各向同性的,初始应力场与地层土自身重力有关,不考虑构造应力;此外,在大埋深地层中,盾构自身重力远小于地层应力,可忽略。
2) 盾构以直线姿态向前开挖推进,圆截面隧洞纵向长度远大于其截面直径,隧洞截面与地层特性沿隧洞走向保持不变,因此,可将圆截面隧洞开挖的力学问题简化为连续体中的孔洞问题,建立轴对称平面应变模型进行分析。
3) 隧洞开挖后,圆截面洞室围岩主要沿径向收敛变形,因此,可认为起临时支护作用的盾构机盾壳通过对围岩施加径向作用力来约束围岩的径向位移。
4) 黏土地层是偏黏弹性材料,即偏应力与偏应变呈黏弹性关系。
简化后的平面应变计算模型如图1所示。图1中,a为圆截面隧洞开挖半径,h为隧洞中心埋深,γ为地层土重度,k为地层土的静止侧压力系数,q为盾壳对地层的径向作用力,x、z为直角坐标系的横坐标与纵坐标,r、θ为极坐标系的极径与极角。
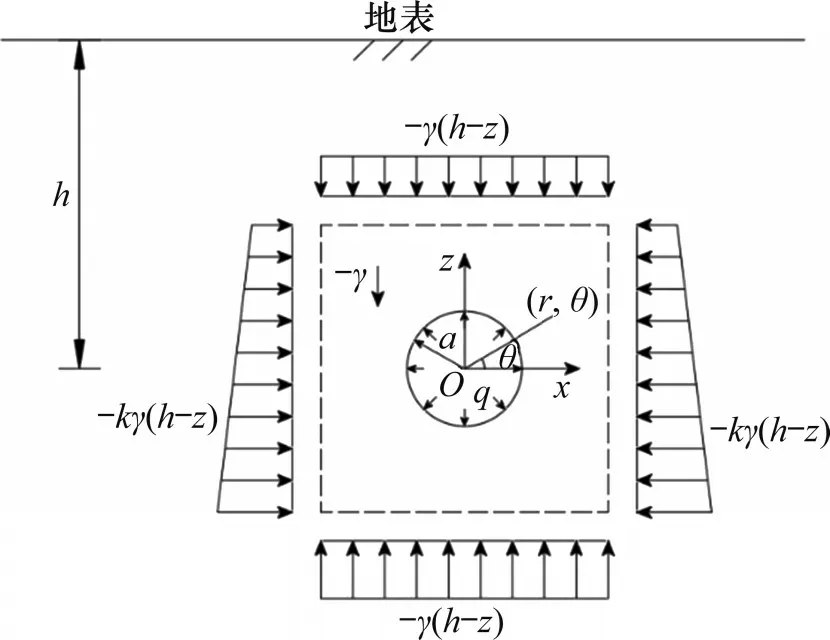
图1 大埋深盾构隧洞-地层力学计算模型Fig.1 Mechanical model of surrounding stratum of shield resuming tunnel
1.1.2 边界条件
由图1可知,该计算模型的边界条件由2部分组成。
1) 在隧洞开挖边界处(r=a),切应力σrθ为0 kPa,径向正应力σrr等于盾壳支护作用力。在rOθ极坐标系下,σrθ和σrr的表达式为
2) 盾构隧洞掘进对地层的影响范围是有限的,在距离隧道足够远处(r→∞),影响范围以外的地层应力等于地层的自重应力,隧洞开挖前后的地层相对位移Δu趋向于0 m,在极坐标系下,该边界的应力和相对位移为
式中:σθθ为环向正应力;ur和uθ分别为径向和环向的绝对位移;u′r和u′θ分别为隧洞未开挖情况(a=0)下的径向和环向绝对位移。
1.1.3 对称性条件
轴对称平面应变模型的几何特征和边界条件均关于z轴(θ=π/2,θ=3π/2)对称,因此,应力和位移关于z轴对称的条件可以表示为
1.1.4 黏土地层本构关系
假设黏土地层为黏弹性体,常用Burgers蠕变模型描述黏弹性体的蠕变行为,如图2所示。经典Burgers本构模型由Maxwell体(弹性与黏性元件串联体)与Kelvin体(弹性与黏性元件并联体)串联而成,是典型的四元体本构模型[24]。Burgers本构模型的蠕变方程为
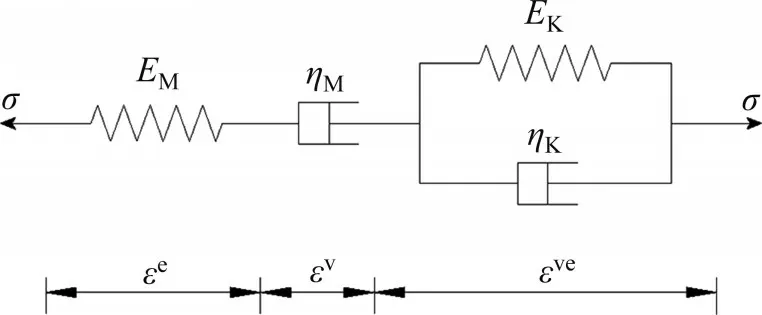
图2 Burgers蠕变本构模型Fig.2 Burgers creep constitutive model
式中:σ为应力;ε为应变;t为蠕变时间;εe和εv分别为Maxwell体弹性应变和黏性应变;εve为Kelvin体黏弹性应变;EM和ηM分别为Maxwell体弹性模量和黏性系数;EK和ηK分别为Kelvin体弹性模量和黏性系数。
材料蠕变过程中任意时刻的应变与应力之比值,称为蠕变柔量J(t),故有
需强调的是,该计算模型可准确描述隧洞附近的地层径向位移,适用于本次研究,然而,由于无法严格满足地表的零面力条件,该法对于计算远离隧道的地层位移存在一定的误差。
1.2 洞周围岩相对径向位移解析解
对于考虑地层应力的黏土地层圆截面盾构隧洞开挖过程的黏弹性问题,可以先求出对应弹性问题的解析解,再根据黏弹性解与弹性解的对应原理[25],通过拉普拉斯逆变换求出黏弹性问题的解析解。
1.2.1 弹性解析解
据图1所示的弹性平面应变模型可以在给定边界和对称条件下用应力函数法求解得到应力方程,进一步结合弹性本构方程、几何方程求解得到地层位移[25-26]。在rOθ极坐标系下,推导得到径向绝对位移的表达式为
式中:b0、c0、Ac1、bs1、cs1、d1s、ac2、cc2、d2c、as3、、d3s均为待定系数。
E′和υ′可分别由式(9)和(10)求得,S1可以利用距离隧洞足够远处的位移予以确定。
式中:E为弹性模量;υ为泊松比。各待定系数由边界、对称条件求解得到,见式(11)。
盾构隧洞开挖引起的径向相对位移可表示为径向绝对位移与地层应力引起的径向初始位移之差,其中,径向初始位移可认为是隧洞未开挖(a=0)时对应的径向绝对位移,因此,可由式(8)推导得到径向相对位移,见式(12)。
将式(11)代入式(12)可得到径向相对位移的弹性解:
1.2.2 基于拉普拉斯逆变换的黏弹性解析解
基于黏弹性解与弹性解的对应原理,由洞周围岩相对位移弹性解可推导得到黏弹性解的拉普拉斯变换,再对其进行逆变换后得到黏弹性解。由弹性力学可知,剪切模量G、弹性模量E与泊松比υ存在以下关系:
将式(9)、(10)、(14)代入式(13)可得
由径向相对位移式弹性解(式(15))进一步推导得到对应黏弹性解的拉普拉斯变换:
式中:s为拉普拉斯变换参数;为Δur的拉普拉斯变换;为G的拉普拉斯变换,
Qd(s)和Pd(s)均为拉普拉斯变换以后的黏弹性算子函数,具体形式由偏应力-偏应变黏弹性模型确定。
对于Burgers黏弹性模型,由式(6)整理可得偏应力-偏应变关系为
式中:ε为剪切应变(2倍偏应变);σ为剪切应力。
假设黏土层体积不可压缩,蠕变由偏应力引起,由广义Hooke定律可知eij=sij/(2G),代入(17)可得
式中:sij为偏应力张量;eij为偏应变张量。
对比式(18)和(19)可得:
黏弹性算子函数(式(20)和(21))经拉普拉斯变换后可得
蠕变柔量(式(7))经拉普拉斯变换后可得
式中:为拉普拉斯变换后的蠕变柔量。将式(22)和(23)代入式(17),经化简可得
将式(25)代入式(16)可得
对式(26)进行拉普拉斯逆变换,可得洞周围岩相对径向位移的黏弹性解为
1.3 盾壳-地层径向接触应力解析解
由于盾构实际开挖半径a略大于盾壳半径b,故存在一定的超挖间隙δ=a-b≪a,如图3所示。开挖完成初期,尚未接触的盾壳与地层之间不存在接触应力,此时,q=0 Pa;当地层土体向洞内收敛变形至与盾壳接触时,约束地层变形的盾壳支护力q等于盾壳-地层径向接触应力。由于黏土地层蠕变的影响,径向接触应力随时间逐渐增大。

图3 地层与盾壳相对位置示意图Fig.3 Diagram of relative position of surrounding stratum and shield shell
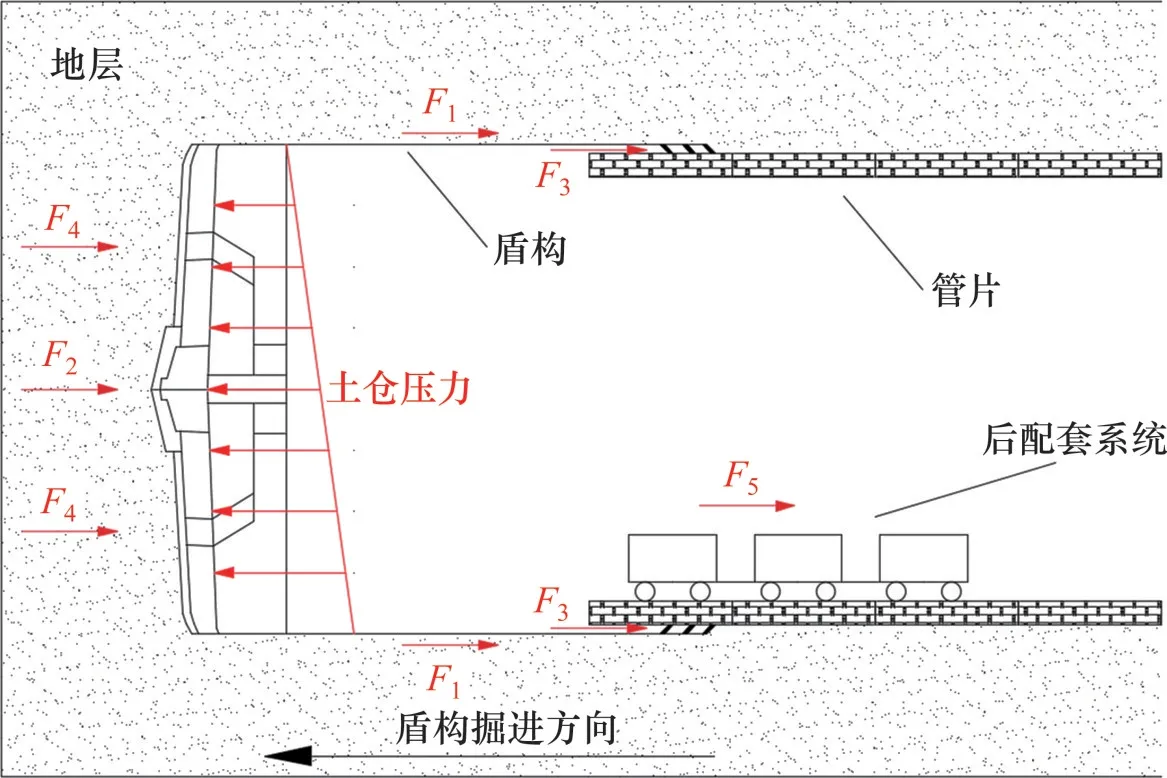
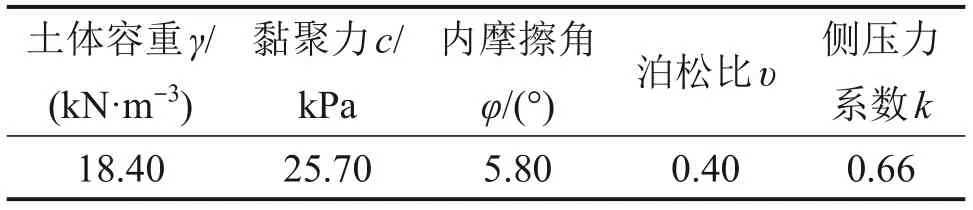
以隧洞开挖时为时间零点,假设地层与盾壳开始接触的时间为t0。当t 由此等式可求得盾壳-地层径向接触应力为 对式(29)进行环向积分可得在横截面内盾壳对地层的接触应力之和为 一般地,盾壳长度L约等于8环管片(单环管片长为1.2 m)的总长度。由于盾构单环掘进工序需要一定的时间Tt,沿盾壳纵向各横截面上地层蠕变的时间不同,故径向接触应力不同。因此,沿纵向将盾壳均分为8个分区,当盾构上一环掘进刚刚结束时,盾壳最前端分区对应的地层蠕变时间为Tt,而盾壳最末端分区对应的地层蠕变时间为8Tt,由此求和得到盾壳-地层总径向接触力G为 盾构推力由盾壳外壁与地层之间的摩阻力、正面推进阻力、盾尾与管片之间的摩阻力、切口环的贯入阻力、后配套系统台车的牵引阻力共5部分组成,如图4所示。金慧等[23]发现盾壳与地层间摩阻力F1占总推力的53.5%~73.0%,因此,对于非正常停机情况,长时间停机使地层充分蠕变,盾壳-地层接触应力增加,进而导致盾壳-地层界面摩阻力增大。假定其他阻力不变,盾构复推总推力增量主要来源于盾壳-地层界面摩阻力增量。 图4 盾构推力组成示意图Fig.4 Schematic diagram of shield thrust composition 当单环掘进工序完成后的额外停机时间为Th时,在式(31)基础上,可进一步求解停机前后的盾壳-地层径向接触力增量ΔG: 当土舱压力维持稳定时,盾构停机复推后的总推力增量ΔF约等于盾壳-地层界面摩阻力增量ΔFf。因此,引入盾壳-地层摩擦因数μ(一般取0.2),可得盾构总推力增量的解析解为 以滇中引水工程昆明段施工4标龙泉倒虹吸盾构隧洞工程为背景,工程应用的盾构机开挖半径a为3.235 m,盾壳总长度L为9.600 m,超挖间隙δ为0.020 m;盾构隧洞全长5.010 km,在大埋深段(中心埋深约70 m)长距离穿越黏土地层,地质参数如表1所示。 表1 地层参数Table 1 Geological parameters 由于地层变化或刀盘扭矩突增需开仓检查或换刀等,盾构在大埋深黏土地层段掘进过程中出现多次长时间停机,因此,采用盾构尺寸与地质参数、停机时长来计算盾构停机引起的盾壳-地层径向接触应力增量,进而计算盾构复推的总推力增量,然后,与现场的盾构复推总推力增量监测结果进行对比,以验证解析解的正确性。 为明确盾构停机段所处黏土地层的蠕变特性,在施工现场通过补勘地质探孔取得原状土样,进行相应的三轴固结不排水蠕变试验,为盾壳-地层接触应力黏弹性解析解提供黏弹性力学参数。 黏土蠕变试验采用GEOTAC应力控制式三轴试验仪,试验施加的围压为依据70 m中心埋深和表1中地质参数求解得到的隧洞地层静止侧向土压力,为850 kPa。试样安装与等向固结完成后,根据黏土试样在既定围压下测得的三轴固结不排水破坏偏应力(377 kPa),蠕变试验的加载方案设计为分三级加载,偏应力分别为100、200和300 kPa,以防止试验中由于加载过大导致试样被突然破坏或仪器被损坏。控制应力加载速率为4 kPa/min,当试样在10 000 s内变形量小于0.01 mm时,认为蠕变已稳定[27],继续进行下一级偏应力加载,直到逐级加载施加完毕。 图5所示为三轴固结不排水蠕变试验在分级加载下的轴向应变-时间曲线(其中,R2为拟合优度)。从图5可见:在850 kPa围压下,不同偏应力的黏土轴向应变-时间曲线呈快速增大、减速增大和稳定变形共3个阶段;随着偏应力加载水平提高,黏土蠕变达到稳定的时间不断增加。使用1stOpt软件中的LM(Levenberg-Marquardt)算法和通用全局优化算法进行拟合,拟合函数参照Burgers本构公式(式(6)),求解得到黏土试样的蠕变力学参数,见表2。将表2参数代入式(7)可得该黏土的蠕变柔量为 表2 黏土试样的Burgers蠕变模型参数拟合结果Table 2 Fitting results of Burgers creep model parameters 图5 850 kPa围压下黏土三轴蠕变试验的轴向应变-时间曲线Fig.5 Axial strain-time curves of triaxial creep test of clay at confining pressure of 850 kPa 针对大埋深段的盾构停机复推工况,收集实际掘进数据,并采用地质参数和试验确定的蠕变柔量,通过式(33)求解不同停机时长下的推力增量理论值。由于盾构单向掘进,盾构在位于隧洞末端的较大埋深段掘进时需要长距离运输物料及渣土,因此,正常掘进一环工序的时间Tt较长,计算时取2.5 h。推力增量理论值与实际值的对比如表3所示。 表3 大埋深段算例中盾构停机推力增量对比Table 3 Comparison of measured and theoretical values of total thrust increment required for shield resuming tunneling in deep buried tunnel 由表3可知:在不同停机时间工况下,盾构复推的总推力增量实际值与理论值相对误差在25.50%以内,平均误差为13.81%,表明复推总推力增量解析解的预测效果较好。此外,将表3中推力增量与付循伟[28]统计的在盾构埋深约20 m区间段的复推总推力增量进行对比。不同埋深段总推力增量实际值与理论值随停机时间的变化如图6所示。从图6可知:一方面,盾构复推的总推力增量随停机时间延长而增加;另一方面,盾构在较大埋深段复推所需的总推力增量明显大于较小埋深段的总推力增量,这是由于埋深越大的黏土地层所受围压越大,蠕变效应越显著[29],导致盾壳-地层接触应力越大。因此,在大埋深段中,应更加关注和预防长时间停机后过大时复推总推力增量诱发的次生风险。 图6 停机复推总推力增量实际值与理论值对比图Fig.6 Comparison of measured and theoretical value of total thrust increment 实际工程算例结果表明,盾构埋深越大或正常掘进工序之余的额外停机时间越长,盾构复推的总推力增量越大。由式(33)可知,总推力增量还与超挖间隙δ、盾壳-地层摩擦因数μ有关。因此,针对以上影响参数,对敏感性进行分析和并提出有效的风险控制措施。 为了对比不同超挖间隙对复推总推力增量的影响,参照一般盾构机实际情况[30-31],设置超挖间隙分别为1.5、2.0和2.5 cm,其余参数取值参考上述大埋深段数据。不同超挖间隙下盾壳-地层界面摩阻力和总推力增量随停机时间的变化如图7所示。由图7(a)可知:随着超挖间隙增大,界面摩阻力越小,这是因为开挖后地层预留变形量越大,地层应力释放越多,地层与盾壳接触时接触应力和界面摩阻力越小。然而,大超挖间隙工况在停机阶段地层的蠕变效应更显著,接触应力和界面摩阻力在停机阶段前12 h的增长率随超挖间隙增大而增大,计算得到的总推力增量随超挖间隙增大而增大,如图7(b)所示。因此,在盾构实际施工中,刀盘设计直径要略大于盾壳直径,以形成一定的超挖间隙,从而有效减少掘进过程中盾壳-地层界面摩阻力,但不宜设置过大的超挖间隙,以避免出现长时间停机后盾构复推总推力增量过大。 图7 不同超挖间隙下盾壳-地层界面摩阻力和复推总推力增量随停机时间的变化Fig.7 Variation of friction resistance and total thrust increment for resuming tunnelling with downtime under different over-excavation clearances 工程实践[18]表明,往盾壳外注射膨润土进行润滑,可降低盾壳-地层的界面摩擦因数,减少卡机问题。膨润土的稠度和填充情况影响界面摩擦因数。将盾壳-地层界面摩擦因数设置为0.10、0.15和0.20,对比不同摩擦因数下总推力增量随停机时间的变化,结果如图8所示。从图8可见:随着摩擦因数减小,总推力增量显著减小。这是由于当接触应力不变时,摩擦因数减小能使盾壳前进需克服的摩阻力减小,进而总推力增量显著减小。这表明有必要在盾壳上预留膨润土注入口,在长时间停机时预先注入膨润土等润滑材料,能有效减小复推总推力增量。 图8 不同摩擦因数下复推总推力增量随停机时间的变化Fig.8 Variation of total thrust increment required for shield resuming tunnelling against downtime under different friction coefficients 此外,复推总推力增量还与反映地层蠕变特性的蠕变柔量相关。因此,当盾构因长距离掘进或地层变换需主动停机进行开仓检查时,建议将停机位置选择在弱蠕变作用地层,如硬岩层、密实砂层等[15]。 1) 将黏土地层圆截面盾构隧洞开挖力学问题简化为Burgers黏弹性体开挖孔洞卸载的平面应变问题,并考虑自重的影响。从现有的洞周径向位移弹性解出发,通过拉普拉斯逆变换得到相应的黏弹性解,进而根据地层径向位移约束条件推导盾壳-地层径向接触应力的黏弹性解。最后,通过积分和分段计算对停机期间盾构复推总推力增量的理论公式求解。 2) 不同停机时长下复推总推力增量实际值与理论值的平均相对误差为13.81%,证明本文所提出的理论计算方法可靠性较高。大埋深段的盾构复推总推力增量更大,因此,在大埋深段长时间停机后应更关注复推推力控制。 3) 超挖间隙越大,盾壳-地层界面摩阻力越小,复推总推力增量越大;而摩擦因数越小,复推总推力增量越小。因此,为了有效预防大埋深段停机的次生风险,建议盾构刀盘开挖时保留合适的超挖间隙,且长时间停机时宜预先采取往盾壳外壁注入膨润土等润滑减阻措施。 4) 该解析解适用于求解黏弹性地层圆截面隧洞中的盾构复推总推力增量,对于实际土压平衡盾构在大埋深黏土地层中长时间停机引起的次生风险控制具有一定的意义。通过该解析解能可靠预测停机后盾构复推的总推力增量,并评估各次生风险控制措施的效果。2 盾构停机复推推力增量解析解
3 工程案例验证
3.1 黏土蠕变参数确定

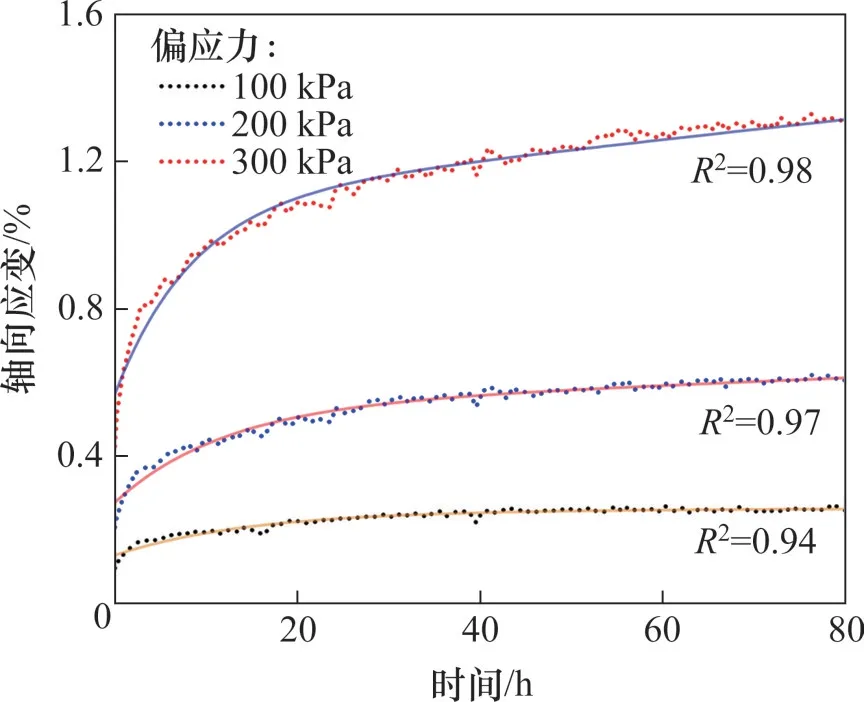
3.2 复推总推力增量计算与对比验证

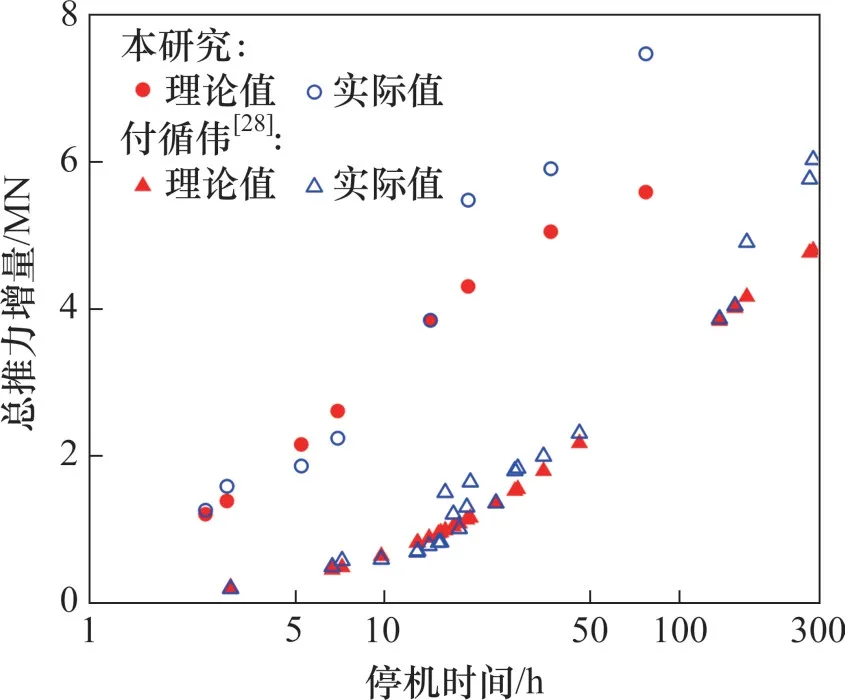
4 参数敏感性分析
4.1 超挖间隙δ的影响
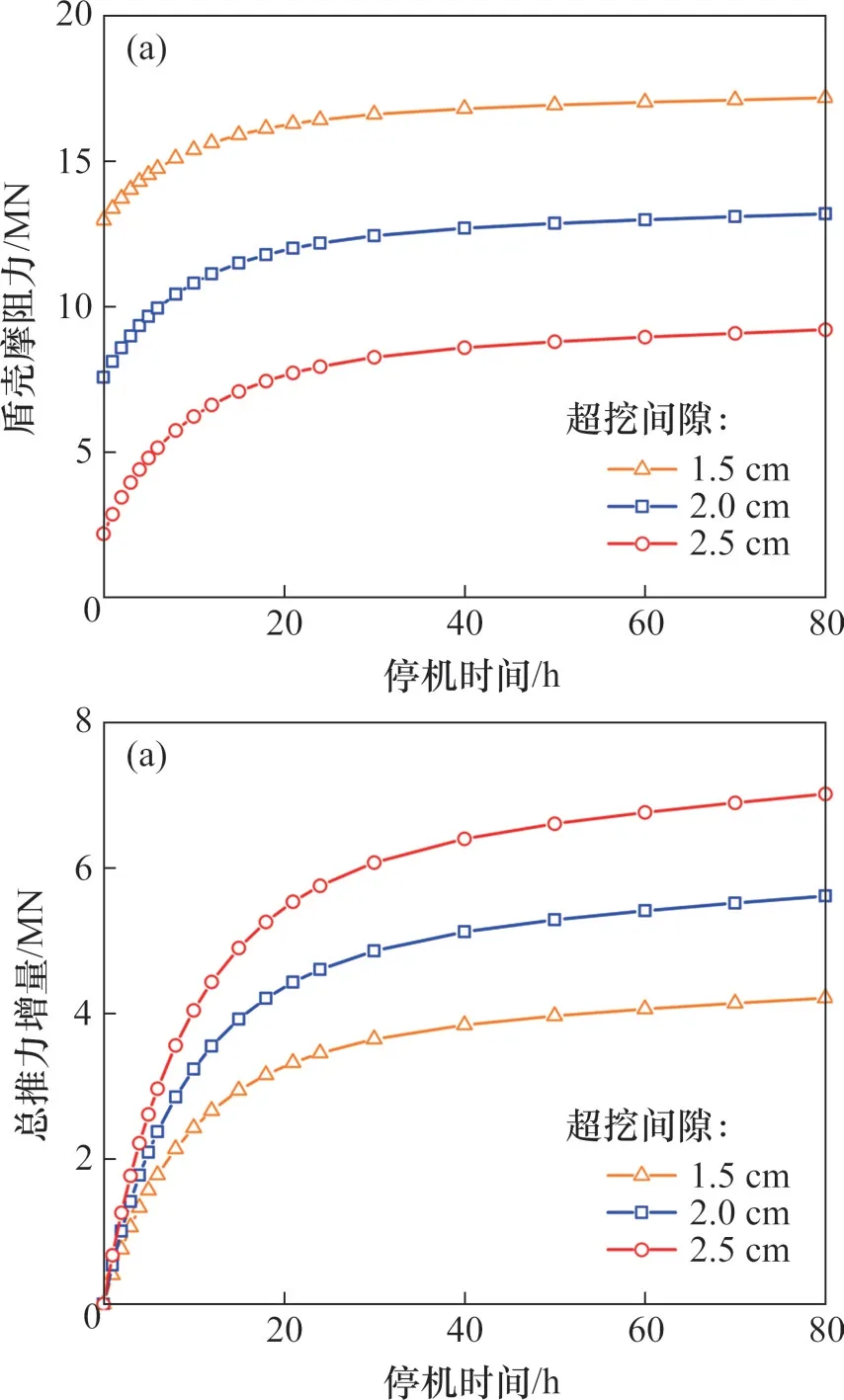
4.2 盾壳-地层界面摩擦因数μ的影响
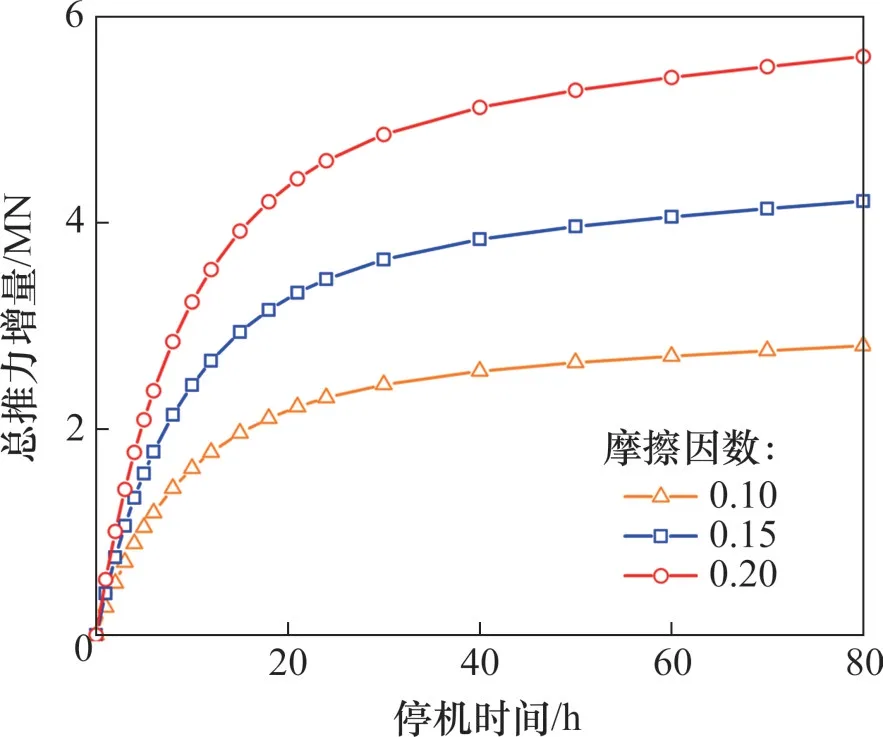
5 结论
