水下旋翼式平台近水底扰动定深控制方法研究

2024-03-01宋智斌黎时宇戴建生

中南大学学报（自然科学版） 2024年1期

宋智斌，黎时宇，戴建生

(1.天津大学机械工程学院，天津，300354；2.天津大学现代机构学与机器人学中心，天津，300354；3.机构理论与装备设计教育部重点实验室，天津，300354；4.南方科技大学机器人研究院，广东深圳，518055；5.伦敦国王学院机器人学中心，英国伦敦，WC2R 2LS)

随着水下航行器设计技术和控制理论的发展，水下航行器已能实现海洋观测以及近海底操作等任务，被广泛应用于海洋科学研究、海洋工程作业、国防军事等领域[1]。近年来，随着海洋工程的深入发展，人们对水下航行器的控制精度和抗干扰能力的要求逐步提升。

旋翼运动方式以其结构简单、机动性好、自主悬停等优点在无人机领域得到广泛应用[2]。由于水和空气之间存在相似性，一些研究人员将旋翼运动模式用于新型水下航行器。旋翼式水下机器人相较于传统水下航行器，可以实现定点悬停，适合执行小范围内的水下抓取、探索等复杂任务。PIERROT等[3]创造性地提出了6旋翼式布局，并在理论上证明了其可行性。RANGANATHAN等[4]提出了一种四旋翼水下机器人“AQUAD”，并对其控制器进行了仿真实验。边靖伟等[5-7]开发了一种新型类四旋翼无人水下航行器(QUUV)，采用滑模控制方法设计控制器，并在水池中进行仿真和实验验证，同时给出了QUUV的控制分配方法。宋保维等[8-9]基于流体力学方法，对水下四旋翼的外形进行优化减阻，为航行器的外形设计提供了参考。TAN等[10]提出了一种可变形的水上四旋翼飞行器，其旋翼可以在不旋转机身的情况下变化方向。JI等[11]以低成本水下观测为目标，提出了一种新型动态水下航行器(NDUV)；对动力学模型进行了分析，并提出了一种模糊PID控制器来控制航行器的下潜深度和姿态。LI等[12]提出了一种新型跨介质吸附仿生机器人，结合四旋翼无人机和仿生鲫鱼吸盘，利用自适应变形的折叠桨叶在水/空介质之间实现稳定、连续、快速跨越切换。

可以看出，旋翼式水下平台系统的合理性已经得到了初步的理论验证，其稳定的近水底悬停性能是水下机器人系统在执行水下抓取、探索、观测等任务所需要的关键性能。水下旋翼式平台在靠近水底工作时，推进器所产生的水流会对水底产生一定的冲击，从而产生未知时变的非线性反冲击力，给平台带来扰动。同时，系统内部的参数不确定性也会影响水下平台的稳定性与控制精度。有效消除水底反冲击力干扰与参数不确定共同产生的非匹配不确定性是水下旋翼式平台顺利完成相应任务的前提。然而，针对水下旋翼式平台在近水底反冲击力作用下运动控制的研究尚未有相关报道。

现有水下旋翼式机器人的控制方法包括传统控制方法即PID控制和先进控制方法。BIAN等[6,13]利用滑模控制实现了水下类四旋翼航行器的运动控制，对于模型中有确定界的匹配干扰有较好的控制效果，但对于具有不确定界的干扰则无法满足控制要求；自适应控制[14]适用于不确定干扰边界为常值的情况，在理想情况下随时间趋于无穷而渐近收敛，但在实际应用中难以保证其瞬态性能；模糊控制[11,15]虽然无需数学模型，但其规则和隶属函数设计缺乏系统性；神经网络控制[16-17]能得到一些理想的结果，但实时控制比较耗时，计算量大；任杰[18]利用模型预测控制实现了水下四旋翼的定深控制，其能够处理各类约束条件，但实时性差，计算复杂度高，参数选择较为困难。

针对以上研究，本文提出一种基于干扰观测器的鲁棒非线性控制器。该控制器采用动态面控制(dynamic surface control, DSC)处理系统的非线性特性，利用一阶低通滤波器对虚拟控制律进行滤波，将微分运算转换为简单且易于实现的代数运算，降低控制算法复杂性[19-20]，使系统离散化，以便将算法移植到单片机中；将水底反流冲击力产生的时变不确定界的非线性干扰和参数不确定性一同视作未知扰动的一部分，采用扰动补偿技术克服系统内外部总扰动，有效地处理近水底任务所带来的未知反冲击力，同时解决系统内部的参数不确定性问题，相比于DSC控制器和串级PID控制，有效地提高了在不确定界干扰下的定深稳定性。

本文建立水下旋翼式平台运动学及动力学模型，该模型考虑了作用于系统的流体惯性力及流体阻尼力，其精确度更高；将系统内部的参数不确定性视为外部干扰而不是变化的物理参数，使系统成为非线性时不变系统，这样，DSC方法就可以处理系统的非线性特性；同时，通过非线性干扰观测器(nonlinear disturbance observer, NDO)有效地处理系统内外部总扰动引起的时变不确定性；通过数值仿真及样机实验，验证所提出的控制器的有效性和鲁棒性。

1 水下旋翼式平台数学模型

水下旋翼式平台(underwater rotor-type platform, URP)的结构设计借鉴了四旋翼结构设计。下面根据ANTONELLI[21]提出的水下航行器建模理论并结合牛顿-欧拉方法建立URP的运动学模型和动力学模型。

水下旋翼式平台示意图如图1所示。M1、M2、M3和M4这4个推进器的布置采用X形结构，推进器M1和推进器M3呈顺时针旋转，而推进器M2和推进器M4呈逆时针旋转。平台的运动由4个可控的自由度(横摇、纵摇、艏摇和垂荡)组成。URP的姿态和运动可以通过调整每个推进器的旋转速度来控制。

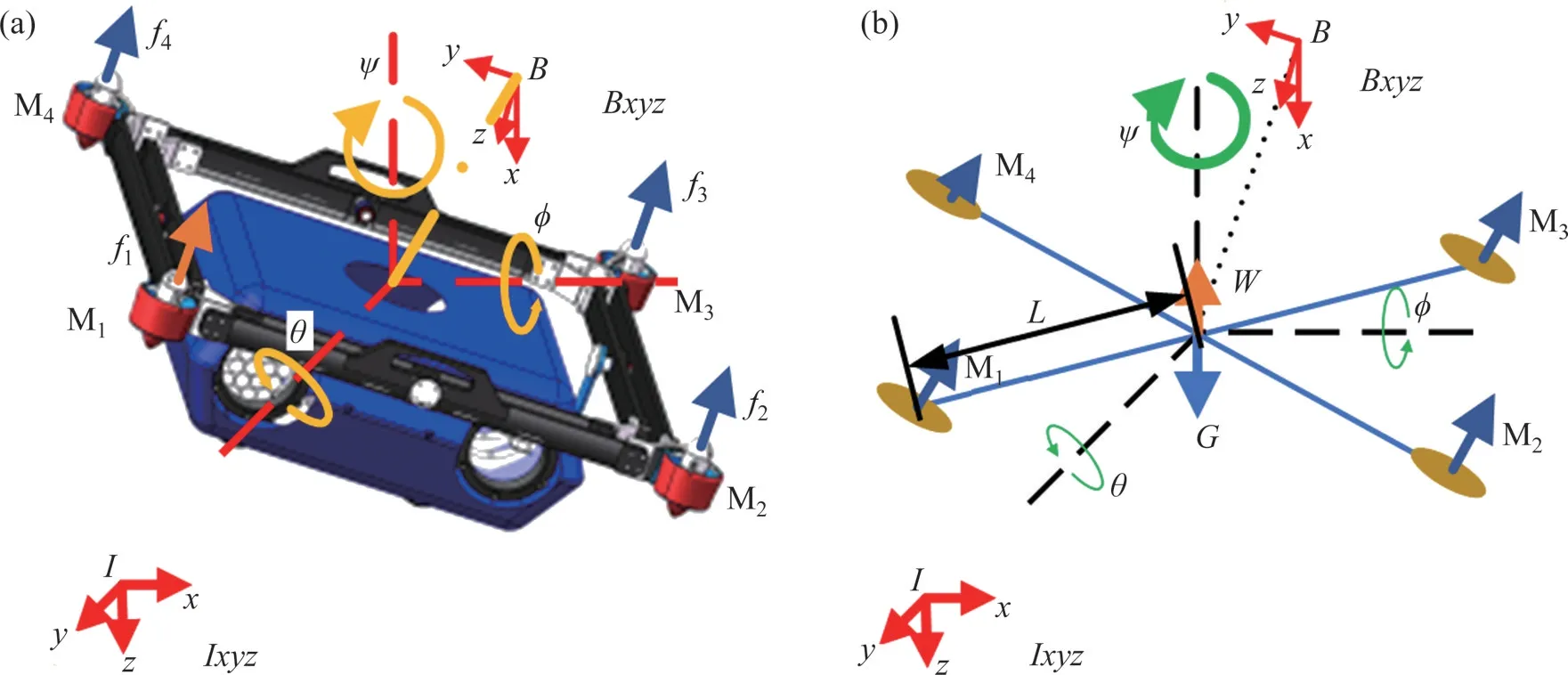
图1 水下旋翼式平台示意图Fig.1 Schematic diagram of URP

为了便于水动力分析，引入2个参考坐标系即惯性坐标系Ixyz和运动坐标系Bxyz。水下旋翼式平台的运动学方程可表示为

其中，η1=[x,y,z]T和η2=[ϕ,θ,ψ]T分别表示URP在惯性坐标系下的位置向量和旋转姿态角向量，ϕ、θ、ψ分别为横摇角、纵摇角、艏摇角=和分别表示η1的一阶导数和二阶导数；和分别表示η2的一阶导数和二阶导数；v1=[u,v,w]T表示URP在运动坐标系下x、y、z方向的线速度；v2=[p,q,r]T表示URP在运动坐标系下绕x轴、y轴、z轴旋转的角速度；和分别表示v1和v2的一阶导数。

RIB和J(η2)分别表示运动坐标系到惯性坐标系的旋转矩阵和角速度的雅可比变换矩阵，其表达式如下：

为了给控制器设计一个准确和合适的数学模型，对URP系统进行以下假设：

1) URP是一种刚体，无内部作用力和形变；

2) URP的重心与运动坐标系的原点重合；

3) 根据实际运动情况，要求ϕ和θ满足|ϕ|<π/2和|θ|<π/2。

根据牛顿第二定律，水下航行器的6-DOF标准模型的矩阵形式可以用下式描述：

其中，v=[v1T,v2T]T；M为惯性矩阵；C为科氏力系数矩阵；D为阻尼力系数矩阵；g(η)为恢复力矩阵；向量τ为推进器产生的力/力矩。

惯性矩阵M由刚体质量矩阵MRB和附加质量矩阵MA组成，可表示为

其中：m为平台的质量；Ic=diag{Ix,Iy,Iz}；Ix、Iy、Iz是x、y和z方向的转动惯量。

同样地，科氏力系数矩阵C(v)由刚体科氏力矩阵CRB和附加科氏力矩阵CA组成，可表示为

阻尼力系数矩阵可表示为

其中，Xu、Yv、Zw、Kp、Mq和Nr为线性流体动力项。

恢复力[22]由平台所受重力(G=mg)和浮力(W)的合力/力矩组成，其中，g为重力加速度。根据假设2)可得，重心坐标为[0, 0, 0]，浮力中心坐标为[0, 0,zB]，因此，可以得到恢复力g(η)为

URP所受力/力矩是由4个推进器提供的。4个推进器的速度为ωi(i=1,2,3,4)，可得URP的总升力和力矩为

其中：cT和cQ分别为推力系数和反扭矩系数；L为推进器到运动坐标系原点的距离；U1为运动坐标系下z方向推进器所输入的力；U2、U3和U4分别为x、y、z方向推进器所输入的力矩。输入的力/力矩向量可表示为

惯性坐标系下的动力学模型反映了系统产生的力和以惯性坐标系为度量的运动状态之间的关系，适用于平台的空间位置控制。因此，可以采用惯性坐标系下的位置动力学方程，以便于设计控制器。而物体的旋转运动在惯性坐标系下会更加难以描述，因此，采用运动坐标系下的姿态动力学方程。将式(7)、(9)、(10)、(11)、(12)、(14)代入式(4)可以得到新的动力学模型：

2 控制器设计

本文提出一种基于干扰观测器的动态面控制器(DSC-NDO)。URP具有4个可控自由度，系统水平方向的运动是通过姿态变化产生水平分力来实现的，因此，本节选取3个姿态通道和深度通道组成的子系统进行控制器设计。

URP在靠近水底工作时，其姿态角的稳定及其深度控制是完成任务的保障。然而，由于水下系统复杂的动力学特性，如固有的非线性和时变特性等，会产生系统内部的不确定性，进而影响整个系统的稳定性与控制精度。本节采用动态面控制(DSC)跟踪各通道的期望信号。由于加入扰动后，很难保证姿态控制的稳定性以及扰动下的零误差，因此，引入干扰观测器(NDO)对扰动进行估计，并通过输入加以补偿。

以姿态通道为例，将系统内部模型参数的不确定性与位置通道对该通道的影响当作内部扰动，与环境扰动一同视为该通道的总扰动。设计干扰观测器(NDO)实时估计扰动量进而补偿控制器，以保证在不确定扰动条件下系统的稳定性；同时，使用动态面控制(DSC)处理系统的非线性特性。所提出的基于干扰观测器的动态面控制器(DSCNDO)的控制策略如图2所示。通过4个通道的给定期望量和反馈量得到由DSC-NDO产生的虚拟控制量U1、U2、U3和U4，转换后得到4个推进器的控制量，从而实现系统的控制。

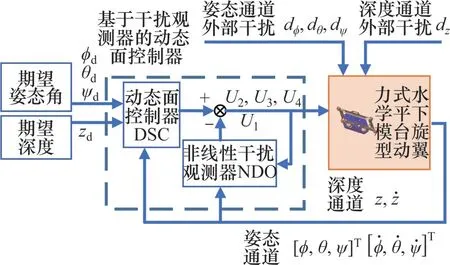
图2 基于DSC-NDO的控制策略Fig.2 Control strategy based on DSC-NDO

2.1 干扰观测器设计

在水下运行过程中，水下旋翼式平台的横摇角ϕ和纵摇角θ较小，故可对URP的运动学方程进行简化，得到如下关系式：

实际应用中的扰动随时间变化，可用非线性项d=(dϕ,dθ,dψ)T和dz分别表示姿态通道的干扰项和深度通道的干扰项。以姿态通道为例，令结合式(15)，可将系统动力学方程改写为

其中：ξ1=[x1,x3,x5]T；=ξ2=[x2,x4,x6]T；g=diag{g1,g2,g3}；Uattitude=[U2,U3,U4]T；f=[f1(x,t),f2(x,t),f3(x,t)]T；Kpx2-z0Wcosx3sinx1；f2(x,t)=h2(x,t)∙g2；g2=

针对系统的综合扰动，构造对扰动d的非线性干扰观测器NDO进行观测补偿[23-24]，其形式如下：

定义非线性干扰观测器的观测误差为

由于干扰项d是未知的，在没有先验知识的条件下，当d相较于控制系统的动态特性变化缓慢时，即认为=03×1，根据式(20)可得：

定义Lyapunov函数Vd=，对其求导可得

为保证干扰观测器的观测误差收敛，需要选择合适的L(x)。取L(x)=diag{c1,c2,c3}，其中ci(i=1,2,3)为正常数，设计非线性函数p(x)=L(x)ξ2。

由Lyapunov稳定性判据可知，干扰观测器是渐近稳定的，最终可以收敛到0，且观测器的指数收敛速度可通过改变L(x)进行调整。

深度通道参数设计如下：

其中，c4为正常数；Γz为深度通道非线性观测器的内部状态参数。

2.2 基于干扰观测器的动态面控制器设计

基于2.1节改写的动力学方程，定义误差变量e1为

其中：ξ1d=[x1d,x3d,x5d]T；x1d、x3d、x5d为姿态通道期望量；和分别表示ξ1d的一阶导数和二阶导数。

构建虚拟控制量Ωd：

其中：K1=diag{k11,k12,k13}；k1i>0(i=1,2,3)，为待设计参数。

为减少控制器的计算量，引入一阶低通滤波器：

其中，为的一阶导数；T1=diag{τ11,τ12,τ13}；τ1i>0(i=1,2,3)，为待设计时间常数。

定义一阶滤波误差γ1为

虚拟误差e2为

设计合适的控制输入：

其中：K2=diag{k21,k22,k23}；k2i>0(i=1,2,3)，为待设计参数。

对于深度通道，同样定义误差变量e1z=z-zd，其中，zd为深度通道的期望深度。

下面对系统的稳定性进行证明。

引理1给定任何实数向量x,y∊R3，以下关系始终成立：

证明通过0≤(x±y)2可得到式(31)。

以姿态通道闭环系统为例，定义Lyapunov函数如下：

对式(32)求导可得：

将式(26)、(27)和(29)代入式(33)可得

由2.1节可知，干扰观测器的观测误差可以在有限时间T内收敛到零，即d=，则式(34)可简化为

结合式(27)，对γ1求导可得

将式(36)代入式(35)可得

根据引理1和Young不等式可知

其中，ε是任意小的常数，且ε>0。

考虑到虚拟控制信号Ωd的导数是有界的，即其中，B1为非负连续连续函数，定义辅助变量：

式中：i=1,2,3。

对式(38)进一步处理可得：

引入紧集Ω1和Ω2：

其中：χ为足够大的正数；p1≥V1(0)，为正常数。故此时Ω1×Ω2也是紧集，由此可知，在V1≤p1成立时，B1在Ω1×Ω2上存在最大值M1。

按照如下条件设计控制参数:

其中：α>2p1/ε，为常数。

在Ω2的边界，V1=p1，则≤-αp1+ε/2<0，因此，V1≤p1是一个不变集，即在全局内V1(0)≤p1的条件下，V1(t)≤p1。

对式(43)两端进行积分可得

由式(44)可知V1(t)是有界的，故存在某一有限时间t>0，使得结合式(33)可知通过合理调整参数，在保证系统稳定性的同时，能够使跟踪误差收敛到任意小。由此可证，姿态闭环系统的所有信号都是半全局一致且最终有界的。同理可对深度闭环系统稳定性进行证明。

综上，结合非线性干扰观测器观测得到的干扰估计值可知，姿态通道的输入Uattitude为

同理可得深度通道的输入为

3 数值仿真及结果分析

为了验证本文所提出控制策略的优越性与有效性，采用MATLAB/Simulink进行数值仿真。此外，为了模拟实际情况中水底反流对平台的随机扰动，如水中漩涡、摩擦流等未知干扰，验证干扰观测器对扰动控制的有效性，在动力学方程中添加高斯分布的白噪声随机扰动，同时加入模型参数不确定性，在复合扰动的条件下将其控制效果与动态面控制器(DSC)和串级PID控制器的控制效果进行对比，测试其期望指令的跟踪能力。在0～30 s对系统姿态通道添加平均幅值为7.5 N·m、采样频率为5 Hz的随机扰动；在深度通道添加平均幅值为10 N、采样频率为5 Hz的随机扰动；同时设计模型参数不确定度为20%，即相应模型参数变为原来的80%。水下旋翼式平台模型参数和控制器设计参数分别如表1和表2所示。其中，串级PID控制器外环采用角度反馈PID闭环控制，内环采用角速度增稳反馈PID控制。DSC控制器设计如式(47)所示，即未考虑扰动补偿项。

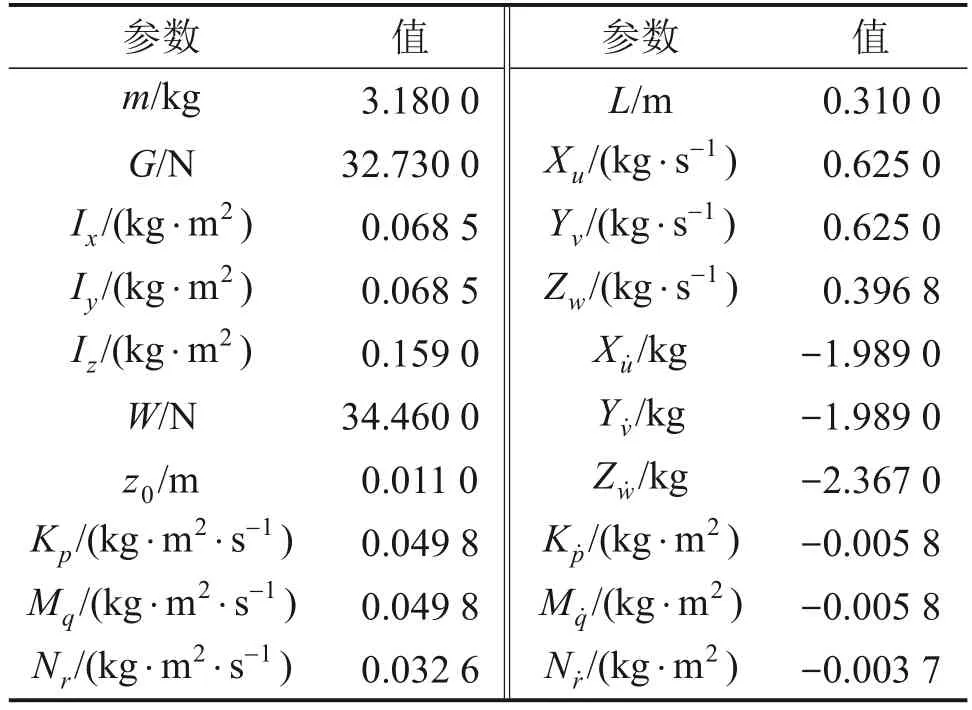
表1 水下旋翼式平台模型参数Table 1 Parameters of URP model

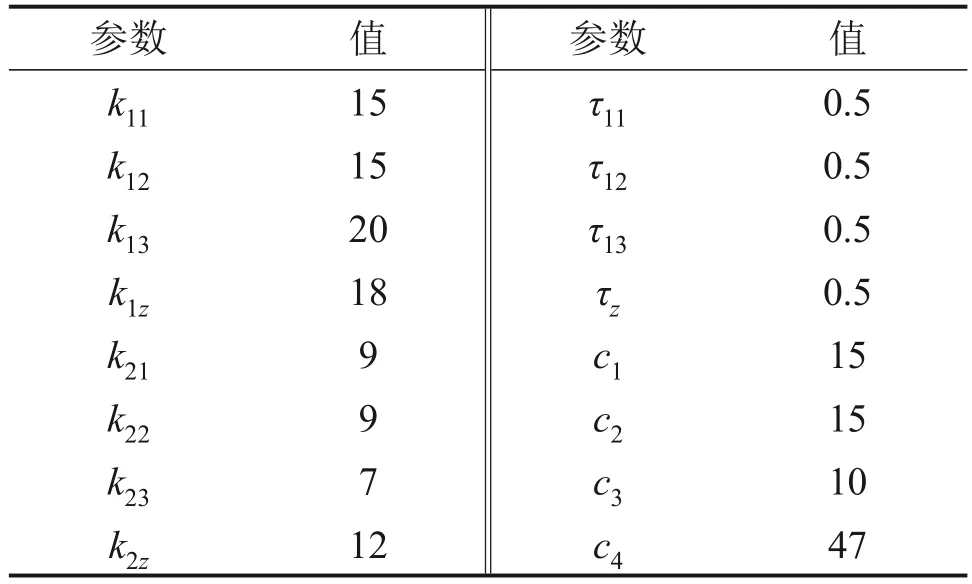
表2 控制器参数Table 2 Parameters of controller

水下旋翼式平台的初始状态值为[x,y,z]T=[0,0,0]Tm，[ϕ,θ,ψ]T=[0,0,0]Trad。在工程中，阶跃信号会使系统面临较为严峻的工作状态，同时又符合许多系统的实际工作情况，所以，常常选用阶跃信号来考察系统的动态性能。如果系统在阶跃输入下的动态性能指标能够符合要求，那么系统在其他形式输入下的动态性能通常也能符合要求。设计水下旋翼式平台的姿态与深度通道参考期望值信号如下：

在串级PID控制器下、动态面控制器(DSC)、基于干扰观测器的动态面控制器(DSC-NDO)下不同通道的响应曲线分别如图3～6所示。在随机干扰和参数不确定的条件下，串级PID、DSC、DSCNDO均保持在期望信号附近。在随机干扰的条件下，通过干扰观测器对扰动进行补偿后，DSCNDO控制器使得姿态通道与深度通道能够快速地达到期望值，同时具有较小的超调量。

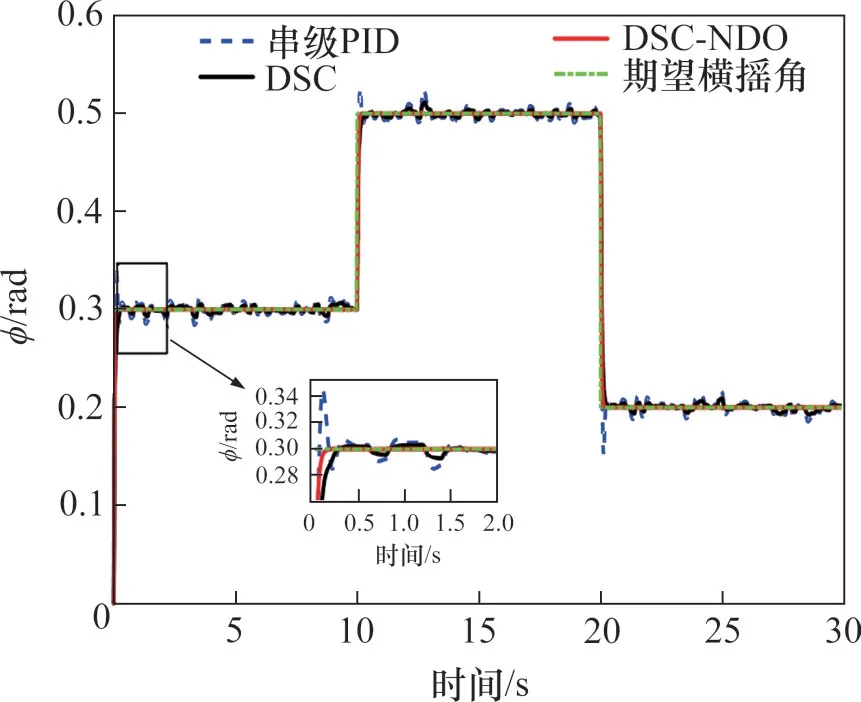
图3 横摇通道响应曲线Fig.3 Roll channel response curves

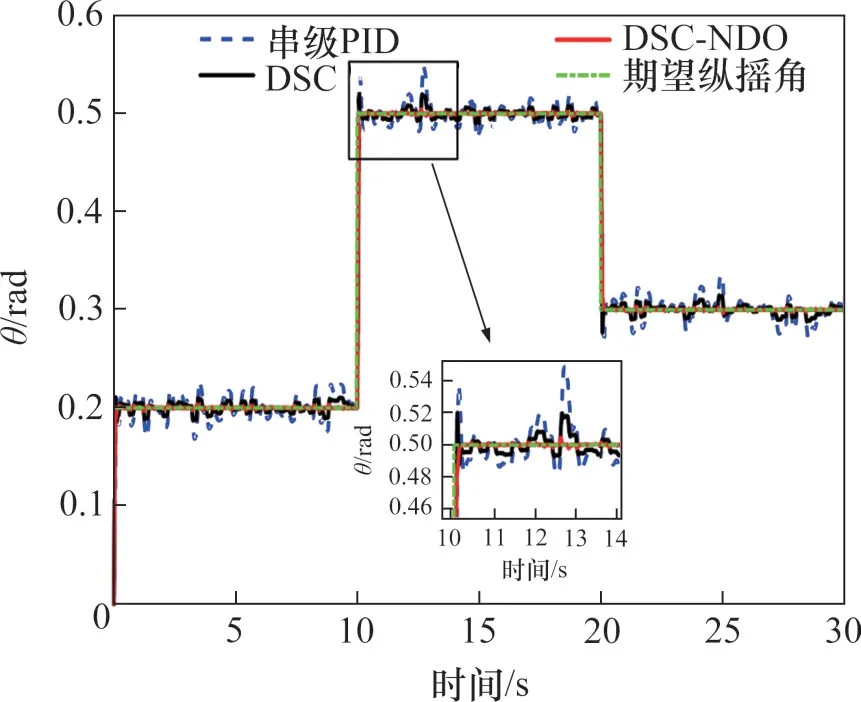
图4 纵摇通道响应曲线Fig.4 Pitch channel response curves

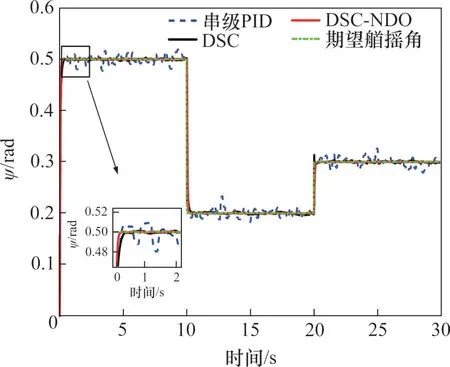
图5 艏摇通道响应曲线Fig.5 Yaw channel response curves

图6 深度通道响应曲线Fig.6 Depth channel response curves

对图3～6中状态量的稳态过程进行定量分析。假设当状态量到达期望值并保持在误差带内振荡时系统进入稳态，分别对图中各个状态量进入稳态后的均方根误差σ和最大误差emax进行计算。

表3和表4所示分别为DSC-NDO控制器、DSC控制器、串级PID控制器下各参数均方根误差和最大误差的对比。由表3和表4可见，URP在DSC-NDO控制器下ϕ、θ、ψ这3个姿态通道和深度通道z的均方根误差和最大误差均比DSC控制器和串级PID控制器的小，能在干扰下高精度地实现姿态跟踪及定深控制。

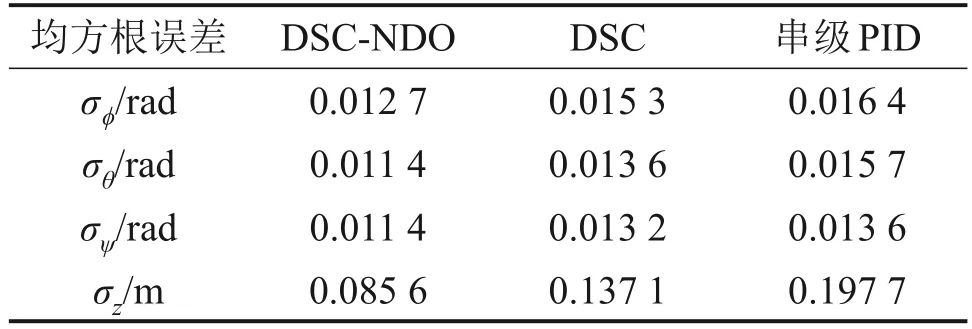
表3 3种不同控制器均方根误差对比Table 3 Comparison of the RMSE of three different controllers

表4 3种不同控制器最大误差对比Table 4 Comparison of the maximum error of three different controllers

以横摇通道为例，姿态通道中深度通道和横摇通道扰动观测器的观测值见图7，所设计扰动包括随机白噪声扰动和参数不确定性。从图7可以看出复合扰动估计与真实总扰动几乎一致，验证了所设计观测器能较好地估计未知的内外部扰动。

图7 复合扰动观测曲线Fig.7 Composite disturbance observation curve

通过上述仿真分析可见，DSC-NDO可以有效解决外部的高频非线性干扰和参数不确定的问题，证明了所设计的控制策略对具有快速时变特性的随机干扰具有有效性和鲁棒性。

4 实验与分析

为了验证本文设计的基于干扰观测器的动态面控制器(DSC-NDO)对水下旋翼式平台系统的实际控制效果，采用自主开发的水下旋翼式平台进行近水底定深悬停实验。

实验平台的电气系统简图如图8所示。水下旋翼式平台控制系统采用STM32控制器作为主控制器，同时集成一系列独立传感器，包括惯性测量单元(IMU)和深度传感器(MS5837)，其中，IMU姿态角的动态精度为0.1°，深度传感器精度为1 cm；远程通信控制链路通过控制手柄和小型2.4 GHz SBus接收器建立，由于电磁波在水中有损耗，信号在水中会很快完全耗散，所以，接收器被封装在漂浮在水面上的小型防水盒中，以便于接收信号，其电缆通过防水电缆穿入内部连接至控制系统；控制器将传感器数据实时传输到PC端上位机中与操作人员通信。整个电气系统都被封装在亚克力圆柱中以保证水密性，两侧通过密封法兰密封，在其侧面有2个O形环密封，在其端面有O形环密封使得外壳完全防水。

图8 实验平台电气系统简图Fig.8 Schematic diagram of electrical system of experimental platform

推进系统主要包括4个推进旋翼，其中电调(electronic speed controllers, ESC)用于控制电机速度。图9所示为推进器静态特性曲线。整个推进器暴露在水中，采用开放式防水。同时为了获得良好的散热条件，ESC安装在防水密封舱外，并采用导热性能良好的环氧树脂密封，以减小密封舱的空间。

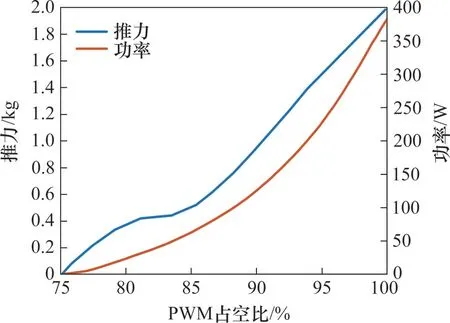
图9 推进器静态特性曲线Fig.9 The statics characteristic curves of the thrusters

在自行搭建的水池中进行测试，水深约为1.2 m，将水下旋翼式平台分别在距水底0.3 m处(水深0.9 m)及0.8 m处(水深0.4 m)进行水下定深实验，设置ϕ、θ、ψ的期望值为0°，定深过程中平台的姿态角度信息和深度信息通过数据传输保存在PC端。分别采用DSC控制器、DSC-NDO控制器和串级PID测试URP的抗干扰性能。实验平台如图10所示。

图10 实验平台Fig.10 Experimental platform

4.1 期望深度为0.4 m的定深控制实验

图11和图12所示分别为当期望深度为0.4 m时URP在DSC-NDO控制器、DSC控制器和串级PID控制器下的运动性能以及推进器的响应曲线。对图11中4个通道的稳态过程进行定量分析。姿态角稳定误差范围及各通道均方根误差分别如表5和表6所示。

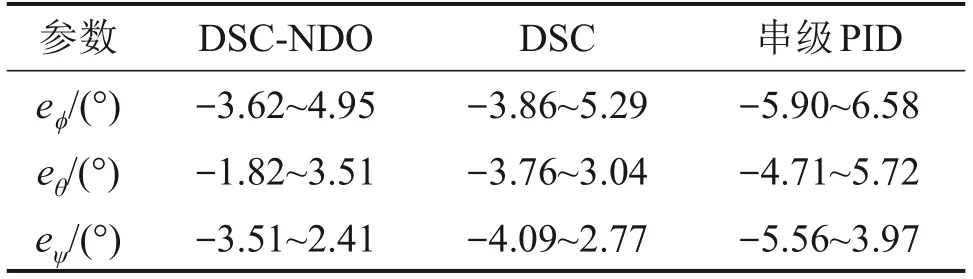
表5 期望深度为0.4 m时姿态通道稳态误差范围对比Table 5 Comparison of steady-state error range of attitude channel with an expected depth of 0.4 m

表6 期望深度为0.4 m时各通道均方根误差对比Table 6 Comparison of RMSE of each channel with an expected depth of 0.4 m

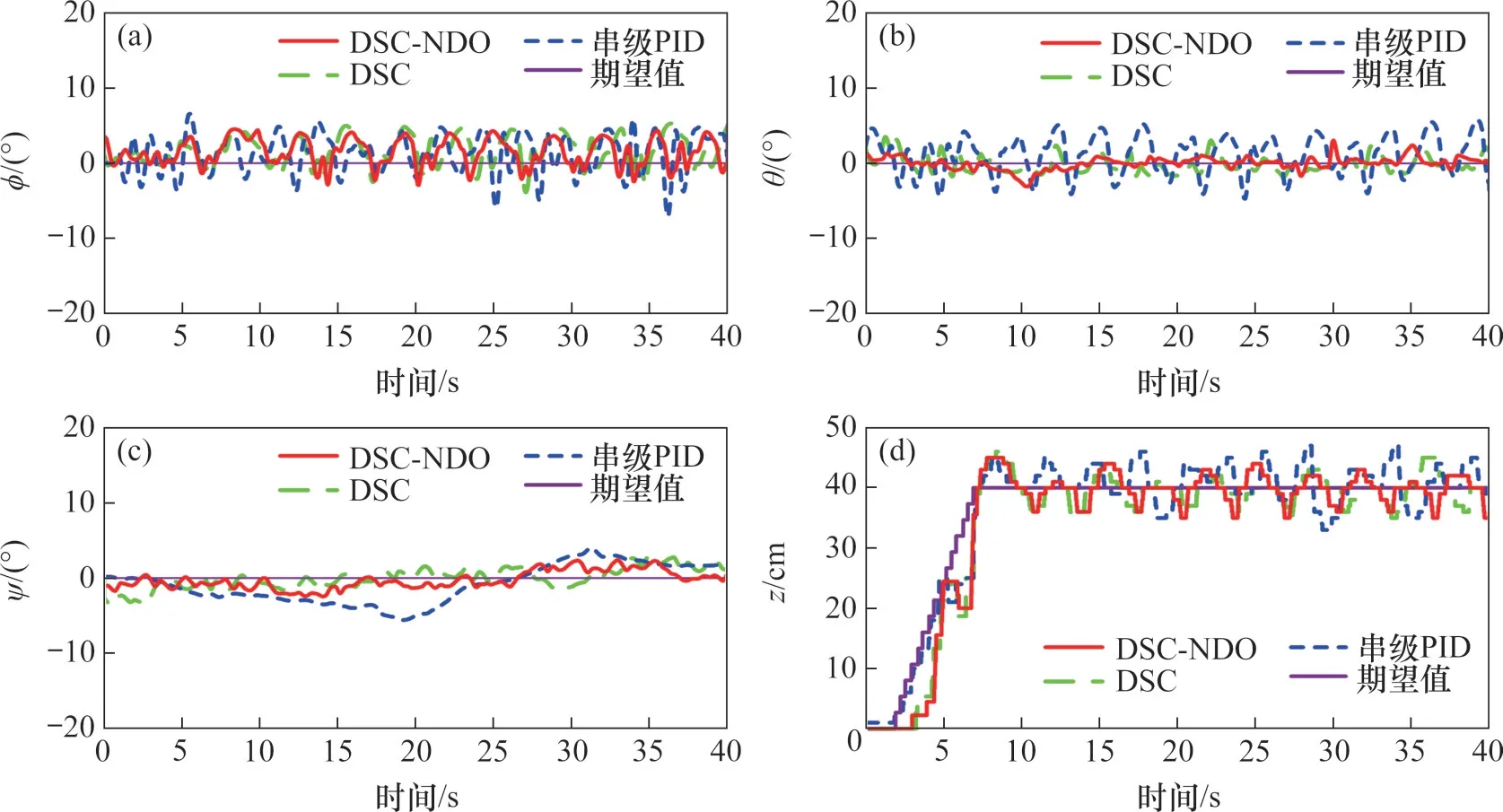
图11 在DSC-NDO控制器、DSC控制器和串级PID控制器下期望深度为0.4 m的运动性能Fig.11 Motion performances with desired depth of 0.4 m under DSC-NDO controller, DSC controller, and cascade PID

对比姿态通道的相关数据可知，在期望深度较小时，URP距离水底的距离较远，水底反冲力对于URP的影响较小。在DSC-NDO控制器下，3个姿态角的稳态误差范围与DSC控制器下的相差不大，其控制精度略有提高；ϕ、θ、ψ的均方根误差相比于DSC控制器分别减小了7.9%、9.0%、7.2%，相比于串级PID控制器分别减小了17.1%、58.5%、51.6%。

在深度通道，由于测量噪声的存在，最终控制输出始终处于调节过程。在DSC-NDO控制器、DSC控制器和串级PID控制器下，z方向在稳态后的误差范围分别为[-5，5] cm、[-5，6] cm、[-7，7] cm，相差不大。同时，深度通道的控制精度有所提高，采用本文方法所得均方根误差相比于DSC控制器减小了8.2%，相比于串级PID控制器减小了25.4%。分析表明在较弱水底反冲击力的干扰下，DSC-NDO控制器能在一定程度上补偿干扰，稳定性更好。当平台定深为0.4 m时，距离水面较近，推进器会使水面产生一定的水波，但其波幅较小，对平台所产生影响可忽略不计。

4.2 期望深度为0.9 m的定深控制实验

图13和图14所示分别为当期望深度为0.9 m时URP在DSC-NDO控制器、DSC控制器和串级PID控制器下的运动性能以及推进器的响应曲线。对图13中4个通道的稳态过程进行定量分析。姿态角稳定误差范围及各通道均方根误差分别如表7和表8所示。

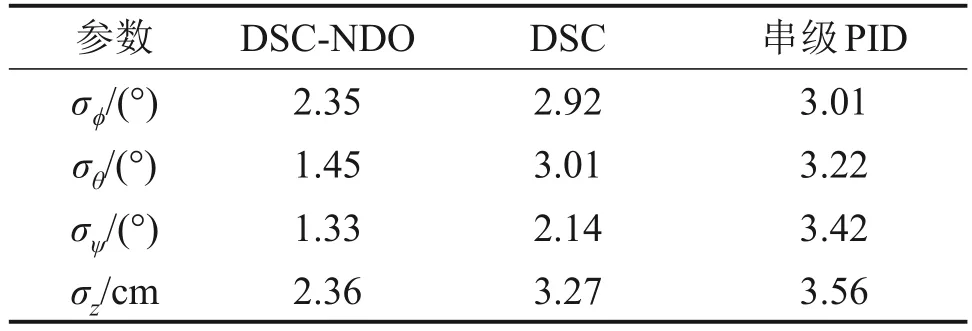
表8 期望深度为0.9 m时各通道均方根误差对比Table 8 Comparison of RMSE of each channel with an expected depth of 0.9 m

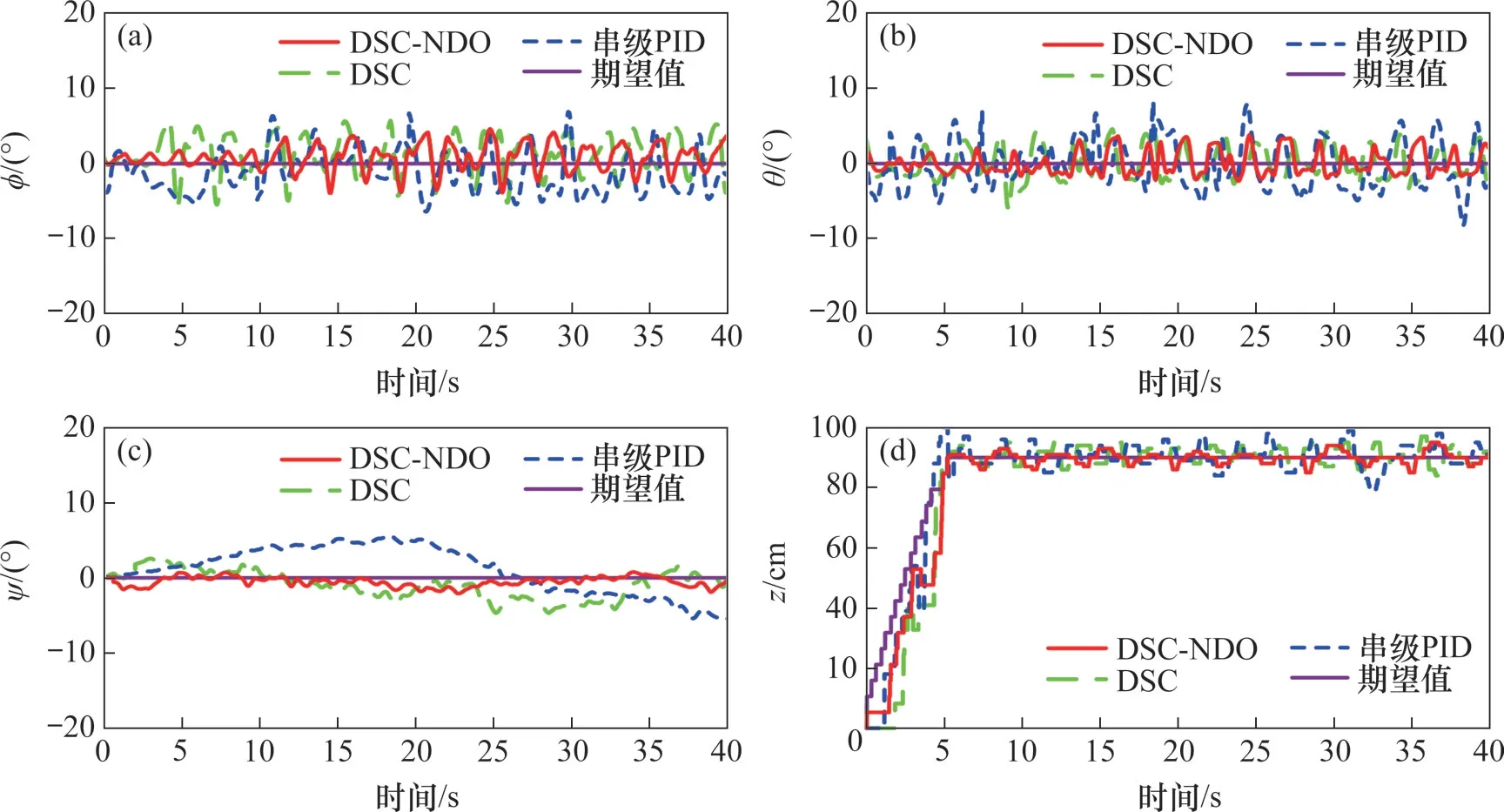
图13 在DSC-NDO控制器、DSC控制器和串级PID控制器下期望深度为0.9 m的运动性能Fig.13 Motion performances with desired depth of 0.9 m under DSC-NDO controller, DSC controller, and cascade PID

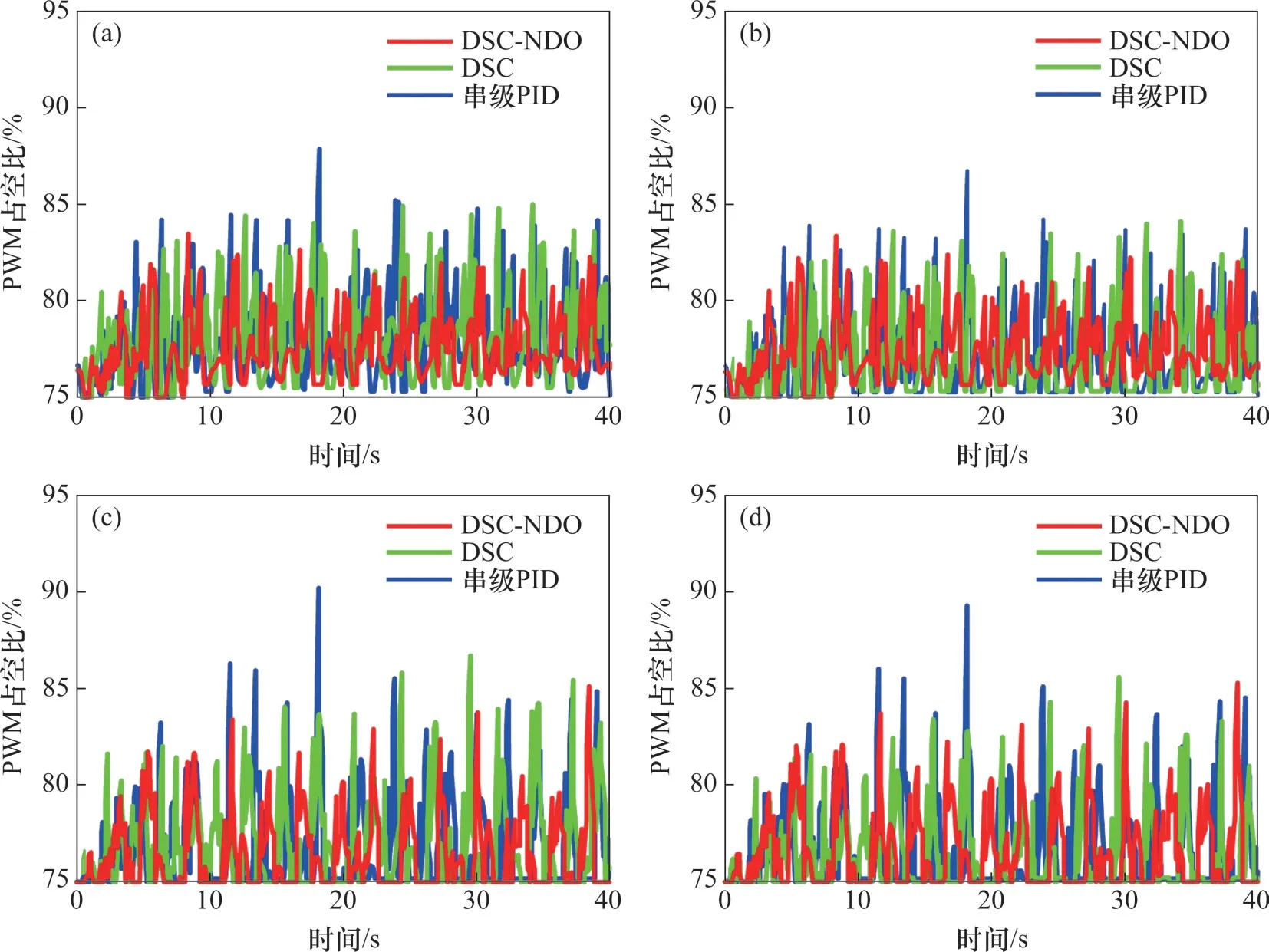
图14 在DSC-NDO控制器、DSC控制器和串级PID控制器下推进器响应曲线Fig.14 Thrusters response curves under DSC-NDO controller, DSC controller, and cascade PID

对比图13中在不同控制器下定深过程中各个姿态角的变化可知，期望深度较大时，URP距离水底的距离较近，为0.3 m，水底反冲击力对URP的影响较大，在其不确定干扰下，姿态系统均会存在一定稳态误差，但采用本文所提出方法时，3个姿态角的稳态误差范围明显比DSC和串级PID控制器的小，ϕ、θ、ψ的均方根误差相比于DSC控制器分别减小了24.2%、51.8%、38.8%，相比于串级PID控制器分别减小了28.1%、55.0%、61.1%。

在深度通道，由于测量噪声的存在，最终控制输出始终处于调节过程。3种控制器的响应时间相差不大，但在本文所提出方法下z方向的震荡幅度明显比DSC控制器和串级PID控制器下的小。由于水底反冲击扰动的影响，在DSC-NDO控制器、DSC控制器和串级PID控制器下，z方向的稳态误差范围分别为[-5，5] cm、[-6，8] cm、[-10，10] cm，控制精度有较大提升。通过对深度通道稳态过程的频域特征进行分析可知，经过傅里叶变换，DSC-NDO控制器的振荡频率约为0.29 Hz，而DSC和串级PID控制器的振荡频率分别约为0.48 Hz和0.49 Hz，本文方法有效减小了定深运动的震荡幅度。同时，采用本文所提出的方法，深度通道的均方根误差为2.36 cm，而其在DSC控制器和串级PID控制器下的均方根误差分别为3.27 cm和3.56 cm，分别减小了27.8%和33.7%。分析表明，在较强水底反冲击力的干扰下，DSC-NDO控制器能较好地降低干扰，提高平台的稳定性。

通过对比2组实验的测试结果可知，在深度为0.9 m(距水底0.3 m)的定深实验中，各通道的控制精度小于深度为0.4 m(距水底0.8 m)定深实验中的控制精度。定深位置越深，水底反冲击力对于平台的干扰越大，由于水底反冲击力干扰持续存在于整个定深过程，使得靠近水底的定深实验误差较大。但通过DSC-NDO控制器可提高URP在干扰环境下的定深稳定性，具有较好的鲁棒性。

因此，本文提出的基于干扰观测器的动态面控制器(DSC-NDO)能够在近水底反冲击扰动的作用下有效提升定深过程中的控制效果，提高了在近水底干扰条件下的姿态通道和深度通道的稳定性，证明了所提出的控制策略的优越性与有效性，这与数值仿真的结果一致。