冰冻地球的进动与章动

刘文亮,欧建文,刘益民,庄妮亚,李义浩,龙光波

(韶关学院 智能工程学院,广东 韶关 512005)

贾尼别科夫效应是指一个刚体绕着它转动惯量最大或最小的主轴旋转时是稳定的,而绕着其他主轴旋转时则是不稳定的[1]. 该效应最初由俄罗斯宇航员弗拉基米尔·贾尼别科夫在空间站维修时偶然发现. 在没有重力影响的情况下,空间站脱落的螺母沿着它所围绕的主轴旋转. 但是对于蝶形螺母,它的旋转主轴会突然掉头,逆向翻转,过了一会又翻转回来,如此反复. 也就是说,蝶形螺母的旋转主轴是不稳定的,会发生180°周期性的翻转. 有人将这种规律联想到了地球,危言耸听地指出地球可能会毁灭于贾尼别科夫效应. 要想知道地球到底会不会发生两极翻转,只要确定地球现在所围绕的旋转主轴是不是介于转动惯量最大和最小值之间的旋转主轴就可以了. 本文通过计算地球模型中3个正交旋转主轴的转动惯量,并分析了地球结冰情况下的转动惯量大小,由此讨论地球旋转主轴所产生的进动和章动变化.

1 转动惯量

转动惯量通常取决于物体的形状,物体内部的质量分布以及旋转轴的位置. 绕定轴转动刚体的转动惯量定义为[2]

(1)

其中,ri为刚体上任一质点到旋转轴的垂直距离,mi为该质点对应的质量.具有规则几何形状的均质物体,其转动惯量可以通过式(1)直接计算得到.

1.1 地球的转动惯量

众所周知,地球不是一个正球体,而是一个赤道略鼓、两极稍扁的不规则球体.作为合理近似,我们把地球视为赤道半径为6 377.83 km,两极半径为6 356.91 km的扁球体,如图1所示.

图1 地球近似为赤道略鼓、两极稍扁的扁球体(结冰纬度为l0,对应球坐标的极角φ=90°-l0)

取O-xyz为扁球体的正交坐标系,O点为地心,xy为地球的赤道平面,z轴穿过地心沿着地球的南北极方向.扁球体方程为

(2)

其中,a=b=6 377.83 km,c=6 356.91 km.根据转动惯量定义式(1),通过三重积分可以容易算出扁球体地球绕3个正交主轴的转动惯量.沿z轴的转动惯量

Iz=∭(x2+y2)ρ(r)dv=

(3)

由于扁球体的对称性,在轨道平面上的2个正交旋转主轴的转动惯量相等

lz=Iy=∭(x2+y2)ρ(r)dv=

(4)

式中ρ(r)为扁球体内部密度随半径r的分布函数.

固体地球可以近似看作由地核、地幔和地壳3层结构组成.李安生利用地震学家布伦从地震波速度推算得到的地球密度数据,拟合出地球内部密度随深度h变化的经验公式[3,4]:

(5)

地球平均半径r与深度h有一简单转换关系:r=637 1-h/km.由于该经验公式缺少地球表层的密度模型,我们假设距离地表0～33 km处的地球密度为一常数ρ0=1.283 3 g·cm-3.那么,固体地球的转

动惯量为

I=Icore+Imantle+Icrust+Isurf

(6)

其中Icore、Imantle、Icrust和Isurf分别表示地核、地幔、地壳和地球表层0～33 km的转动惯量.把式(5)代入式(3),通过分段积分最后得到固体地球绕南北极旋转主轴的转动惯量为:Iz=8.036 5×1037kg·m2.这一结果与现代高精度的空间测地数据得到的地球旋转主轴的转动惯量一致[5].利用式(4),赤道平面上的2个正交旋转主轴的转动惯量为:Ix=Iy= 8.009 7×1037kg·m2.

1.2 冰冻地球的转动惯量

从式(6)的分段积分计算结果可见,地表0～33 km处的地球密度分布对地球总转动惯量大约有0.72%的轻微贡献.为研究地球表层密度对转动惯量的影响,我们做一简单的假设,见图1.假设地球在南北纬度l0以上全部结冰,结冰后采用海冰密度ρ1=0.914 5 g·cm-3;未结冰的南北纬度区域依然采用地表的平均密度ρ0.则地表0～33 km的转动惯量积分公式与球坐标的极角φ有关.

(7)

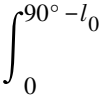
(8)

随着地球南北极结冰纬度的变化,地球沿着3个旋转轴的转动惯量也会发生变化,计算结果见图2.实线是地球绕南北极的自转轴的转动惯量Iz,虚线是绕赤道平面上x(或y)轴的转动惯量Ix(或Iy).由图可见,当全球结冰的时候,此时地球绕南北极方向的转动惯量Iz最小,为8.019 8×1037kg·m2.地球历史上至少出现过3次全球冰冻现象[6].随着海冰的消融,转动惯量Iz急剧上升,直至海冰消融到南北纬度50°的时候,转动惯量Iz上升到了8.036 3×1037kg·m2;当冰冻保持在南北纬度60°以上,地球南北极方向的转动惯量Iz变化得非常微小,几乎保持不变.

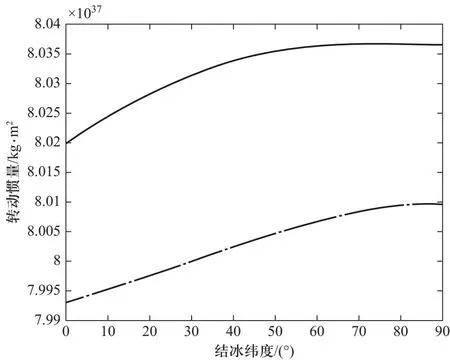
图2 地球转动惯量随着结冰纬度的变化(l0=0°表示全球结冰, l0=90°表示海冰全部融化)

2 三轴刚体地球的旋转

三轴刚体地球的旋转规律可以用欧拉运动学方程结合欧拉动力学方程来共同描述[1,2].如图3构建两组坐标系:固定在地球上的坐标系O-xyz和惯性坐标系O-ξηζ,两组坐标系都以地心O点作为共同原点.

图3 三轴刚体地球运动的坐标系

地球在三维空间中的旋转可以看作是固定坐标系O-xyz相对于惯性系O-ξηζ的整体旋转运动.两组坐标系中,Oxy平面与Oξη平面的交线On称为节线,On与Oξ之间的夹角φ称为进动角,On与Ox之间的夹角ψ称为自转角,Oζ与Oz之间的夹角θ称为章动角.三个欧拉角φ、ψ、θ和沿着地球x、y、z三个方向的旋转角速度ωx、ωy、ωz的运动规律,可以用欧拉运动学方程

(9)

结合欧拉动力学方程

(10)

来共同描述.

2.1 地球不受外力作用下的潘索情况

扁球体地球赤道平面的转动惯量相等,即Ix=Iy≠Iz.本小节讨论简单的地球所受合外力为零的情况,即Mx=My=Mz=0.此时,欧拉动力学方程(10)可以简化为潘索情况[1,2]

(11)

在惯性系O-ξηζ内观察,地球瞬时自转轴也叫天文地轴.天文地轴绕着地理地轴Oz作匀速转动,扫描出一空间锥面,其周期的理论值为[1,7]

(12)

其中,H=(Iz-Ix)/Ix.注意,2π/ωz即为地球的自转周期23.934 4小时,近似等于1天;取地球表层平均密度ρ0=1.283 3 g·cm-3的情况下,Iz=8.036 5×1037kg·m2,Ix= 8.009 7×1037kg·m2,计算得到H≈1/300,因此天文地轴绕地理地轴的变化周期约为300天.然而τ的实际测量值约为400天,这是由于地球所受的外力矩不为0,且地球不是绝对刚体的原因造成的.

随着地球南北极结冰纬度发生变化,Ix、Iz也发生变化,从而引起天文地轴绕地理地轴的周期τ变化,计算结果见图4.由图可见,海冰从赤道消融到南北纬度35°的时候,周期τ由约300天逐渐减小到最小值252天,天文地轴绕地理地轴的周期越来越短,绕转越来越快,地球越不稳定;随着海冰消融的纬度继续扩大,周期τ逐渐变大,等到海冰全部消融的时候,周期τ又恢复到了最大值约300天.也就是说,一半液态水一半冰冻的地球旋转比冰冻地球或者纯液态水地球更为不稳定.

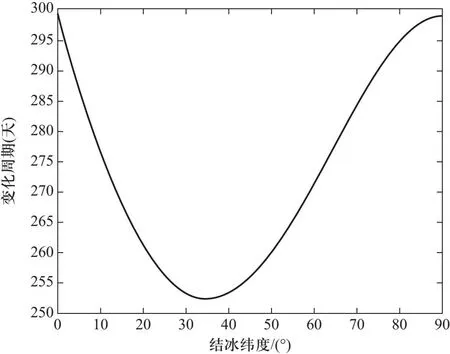
图4 天文地轴绕地理地轴的变化周期随地球结冰纬度变化

2.2 引潮力作用下的地球进动与章动

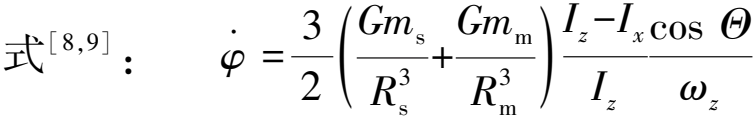
(13)

Δθ=θ-Θ=

(14)

(15)

为章动振幅.Θ=23.433°是黄赤交角,α=5.145 396°是黄白交角,μ是月-地质量比,Tz=0.997 269 672天、Tm= 27.321 661 55天、Tr=6 793.477 061天分别表示地球自转周期、月球的平均轨道周期和白道的旋进周期.表1总结了上述公式中使用的符号所对应的物理含义.

表1 文使用的符号所对应的物理含义

地球与太阳、月球之间的引力相互作用导致地球自转轴的倾斜程度随时间的变化而变化.根据式(13),进动角φ随时间的改变叫做进动,表现为天文地轴绕黄极极轴(图5中的垂直虚线)的圆周运动.章动是天文地轴沿黄极极轴的上下摆动,式(14)表明天文地轴与黄极极轴的夹角在黄赤交角Θ附近作正弦变化,表现为垂直于进动椭圆的切向振动,最大章动角则由式(15)决定.进动与章动的叠加运动,使得天文地轴绕黄极极轴的运动轨迹呈波浪形状,见图5,P、N分别表示地球进动和章动运动.

图5 受太阳、月球的引潮力作用下地球的进动与章动

地球自转轴的进动和章动与位于赤道面的转动惯量Ix和南北两极的转动惯量Iz的组合参数H=(Iz-Ix)/Ix有关.随着地球表面密度发生变化,譬如结冰,Ix、Iz也发生变化,从而改变天文地轴的具体运动轨迹.图6(a)、6(b)分别是地球进动角速度和章动振幅随结冰纬度的变化规律.从图可以看出进动和章动的变化趋势一致,均与H成正比.在冰雪地球融化阶段,从结冰纬度l0=0°到35°,地球转动轴经历了一个进动和章动急剧增大的不稳定阶段.在l0=35°时,章动振幅Namp达到最大11.023 3″,也就是地球的天文地轴相对于黄极极轴偏离了11.023 3″;同样,进动率也达到最大的9.367 8×10-12rad·s-1.当地球南北极只有80°～90°的范围结冰时,地球自转的进动和章动变化平缓,地球自转趋于稳定.地球受到力矩作用的自转稳定性分析与不受力矩作用的潘索情况一致,均指出l0=35°时的冰水混合地球的旋转最为不稳定.

图6 地球进动角速度和章动振幅随结冰纬度的变化规律

以进动作横坐标,章动作纵坐标,天文地轴在三维空间中划过的轨迹线铺展开为二维图,见图7.地球经历55.8年后,即3个白道旋进周期3Tr的时候,不同结冰情况下的地球的天文地轴运动轨迹见图7.虚线、实线、点线分别代表l0=0°、35°和60°地球结冰时的情况.从图可l0=35°时,地球上下摆动(即章动)的振幅最大,并且进动角φ漂移得最远,达到0.016 4 rad.如果地球自转轴固定不变永远指向一个方向,那么Δφ=0 rad、 Δθ= 0″,在图7中则表现为原点中的一个点.

图7 不同结冰情况下地球天文地轴划过的轨迹线

3 结论

地球的进动和章动问题关系到地面上分米级别或厘米级别的高精度定位,以及航天器的精密定轨等生产生活、科学技术等方方面面,因此科学家非常重视其理论研究.随着天体测量精度的不断提高,尤其是全新一代空间天体测量卫星盖亚(Gaia)可以精确观测银河系内数以亿计的恒星,使得对天体位置的测量精度达到10-6角秒量级,与之对应的地球自转理论也随之不断改进. 国际天文学联合会(IAU)为适应这些高精度需求,规范了IAU2006/2000岁差-章动模型[10]. 这些专业模型的概念抽象,计算过程十分烦琐、复杂,对于非专业人士理解起来非常困难.

本文从简单的刚体地球模型出发,通过三重积分计算地球模型的3个正交旋转主轴的转动惯量,然后利用欧拉运动学和动力学方程的理论结果,分析了地球结冰情况下的自转状态. 我们的地球模型物理图像直观,计算过程简单,有利于人们对进动和章动的理解. 我们的研究指出,冰雪地球在融化的过程中,经历了进动和章动急剧变化的阶段,地球自转较为不稳定;在南北纬度80°～90°结冰的地球,其进动和章动变化较小,地球自转较为稳定. 通过我们的计算,否定了地球会毁灭于贾尼别科夫效应的传言.