基于GPU 的LBM 迁移模块算法优化
2024-02-29黄斌柳安军潘景山田敏张煜朱光慧
黄斌,柳安军,潘景山*,田敏,张煜,朱光慧
(1.齐鲁工业大学(山东省科学院)山东省计算中心(国家超级计算济南中心),山东 济南 251013;2.济南超级计算技术研究院高性能计算实验室,山东 济南 251013;3.哈尔滨工业大学能源科学与工程学院,黑龙江 哈尔滨 150001)
0 引言
格子玻尔兹曼方法(LBM)是基于介观定理的离散流体力学计算方法,通过描述粒子在固定格点中的运动来计算流体的运动状态。相比于宏观计算流体力学(CFD)方法需要求解二阶偏微分方程(连续性方程、动量方程),LBM 只需要求解一个一阶偏微分方程(粒子数密度守恒方程)[1-2],通过计算介观微团的碰撞与迁移过程来演变宏观物理过程。除此之外,作为一种瞬态演变算法,LBM 还具有描述简单、易于编程、复杂边界易于设置等特性[3]。因此,该算法在提出不久后,已经广泛应用于计算流体力学的相关领域[4-5]。另一方面,并行计算的出现加速了数值模拟计算的发展,高性能计算(HPC)逐渐在流体研究中扮演了重要角色。经过几十年的发展,并行计算已经发展出了多种成熟的编程模型,其中基于图形处理器(GPU)进行加 速的有OpenCL[6]、OpenAcc[7]、统一计 算设备架构(CUDA)[8-9]等。CUDA 是基于GPU 的一种并行计算平台与编程模型,适合处理大规模的密集计算。
与传统的CFD 算法不同,LBM 算法本身就有着易于并行的特性,适合通过GPU 来对计算进行加速。由于LBM 按照网格点来设计模型,因此计算任务可以按照网格点来分配给各个计算单元[10]。现如今越来越多的研究人员选择GPU 来对LBM 算法进行并行加速,减少了科研计算时间:RAHMAN 等[11]利用GPU 计算基于LBM 算法的幂律非牛顿纳米流体在矩形腔内的磁流体动力学热溶质自然对流流动;WATANABE 等[12]基于LBM 研究多潮汐涡轮机,使用10 台P100 GPU 加速,在9 h 内完成了8.55×108规模网格点对10 台潮汐涡轮机的大规模模拟;KIANI-OSHTORJANI 等[13]在GPU 上 基于LBM 研 究了流体与单个颗粒团簇混合物中的耦合传热问题。
Palabos 是基于LBM 算法设计的计算流体力学软件[14]。经过十几年的发展,Palabos 的功能逐渐完善,能够完成更多的流体模型计算,如血液流动模拟[15]、液滴碰撞[16]、多孔介质[17]等。这些研究表明了Palabos 已经成为一个热门的研究LBM 算法的工具。KOTSALOS 等[18]在研究血液流动时使用了GPU 并行,但是在所提算法中GPU 加速的是有限元法(npFEM),而液体的流动计算是在CPU 上完成计算,因此,他们的研究中也没有将LBM 算法完全GPU 并行。对于Palabos 来说,使用GPU 加速存在的难点是部分计算无法直接按照网格映射到计算单元,直接并行会存在数据冲突。
LBM 含有两个计算热点:碰撞(collide)和迁移(streaming)[19]。前者的计算是对格点本身的数据进行计算,这样并行后每个计算单元直接获取数据就可以完成计算;后者则需要将自身的数据与周边格点上的数据进行交换,这部分存在着一定的数据依赖,不方便展开并行。文献[20]基于Palabos 对LBM算法做了并行优化,由于迁移计算存在数据依赖,其只将碰撞计算部分做了并行,最终达到了1.5 左右的加速比。由此可见,设计迁移模块的并行算法能够进一步提升算法的计算效率。
本文分析LBM 原算法的实现逻辑以及并行化的难点,介绍并行算法的设计思路,测试优化后算法的计算效率,并和原算法进行对比。
1 算法的原理与实现
1.1 LBM
LBM 由玻尔 兹曼方 程演化[21],在模型 建立时一次性完成求解非线性偏微分方程组的工作[22],这样做使得研究人员在数值模拟计算中只需要处理简单的线性方程或方程组。通过离散分布函数,LBM 使用一个碰撞算子来模拟一次迭代内分布函数的演变,由此计算得到密度、压强、内能等诸多流场信息。LBM 在不同案例中的实现流程相似,如图1 所示,核心的2 个计算模块分别是碰撞和迁移。
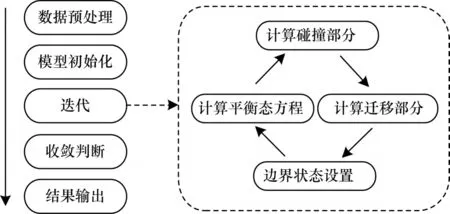
图1 LBM 实现流程Fig.1 Implementation process of LBM
LBM 中的基本模型为DnQm模型(n为空间维度,m为离散格点上的速度分量数量),本文采用的模型为D3Q19,它的速度分量分布如图2 所示(彩色效果见《计算机工程》官网HTML 版本,下同)。

图2 D3Q19 速度分量模型Fig.2 D3Q19 velocity component model
LBM 简化后的核心公式,计算平衡态的分布函数如下:
其中:ωk为各个速度分量的权重;ck为速度分量的方向;cs为无量纲声速;u为速度。之后由碰撞算子来更新分布函数,如下所示:
其中:τ表示平衡态的松弛时间,与宏观下流体的扩散系数有关。
1.2 热点分析
针对算法进行热点分析是并行算法优化前的必要步骤,本文选取Palabos 中的经典案例——三维方腔流动模型。表1 所示为三维方腔流动计算的计算函数热点,该测试的网格数为1 283,其中碰撞与迁移部分计算时间占比超过70%。

表1 三维方腔流动各个计算热点占比 Table 1 Each computing hotspot proportion of three-dimensional square cavity flow case %
之前的工作大多只将碰撞计算部分放在GPU上进行加速[20]。根据模型中的网格,将格点映射到GPU 中的计算单元,每个计算单元负责一个格点中的数据计算。因为存在数据依赖,完成碰撞计算后无法在GPU 继续完成迁移部分的计算,需要将计算结果传回CPU 计算,异构系统上的数据传输产生了大量的时间消耗,所以将迁移计算部分也放在GPU上不仅能够达到更好的优化效果,同时对于迁移计算来说还可以省去数据传输的步骤,提升数据在GPU 端的利用率。
1.3 迁移计算的实现
在迁移计算中,每个格点中的速度分量需要按照一定的规律与周围格点中的速度分量进行数据交换。Palabos 串行计算下迁移计算的伪代码如算法1所示。

上述伪代码中主要执行的是swap 函数,其运算法则如图3 所示。其中:数据a与b代表当前格点中位置i与位置i+9 上的速度分量,数据c与d代表相邻格点中位置i与位置i+9 上的速度分量,1≤i≤9。
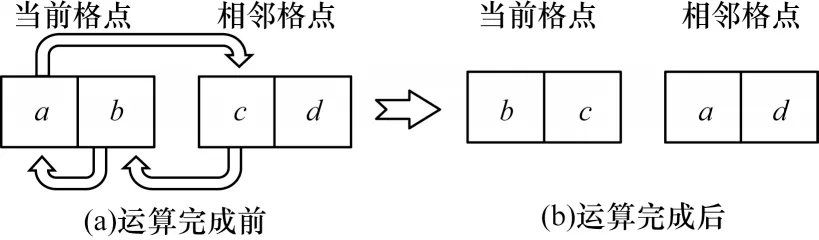
图3 swap 函数的运算法则Fig.3 Operation law of swap function
根据上述伪代码以及图3 中sawp 函数的运算规律可以看出,在迁移计算中,除了中心点0 之外,剩余的18 个点都需要参与数据交换。每次交换涉及3 个数据:两个为格点本身的数据,一个为周围格点上的数据。18 个格点可分为9 组,每组都有一个固定的数据交换方向,如表2 所示。交换方式为:当前格点上位置为i和i+9 的速度分量与对应方向格点中位置i上的速度分量相互交换。
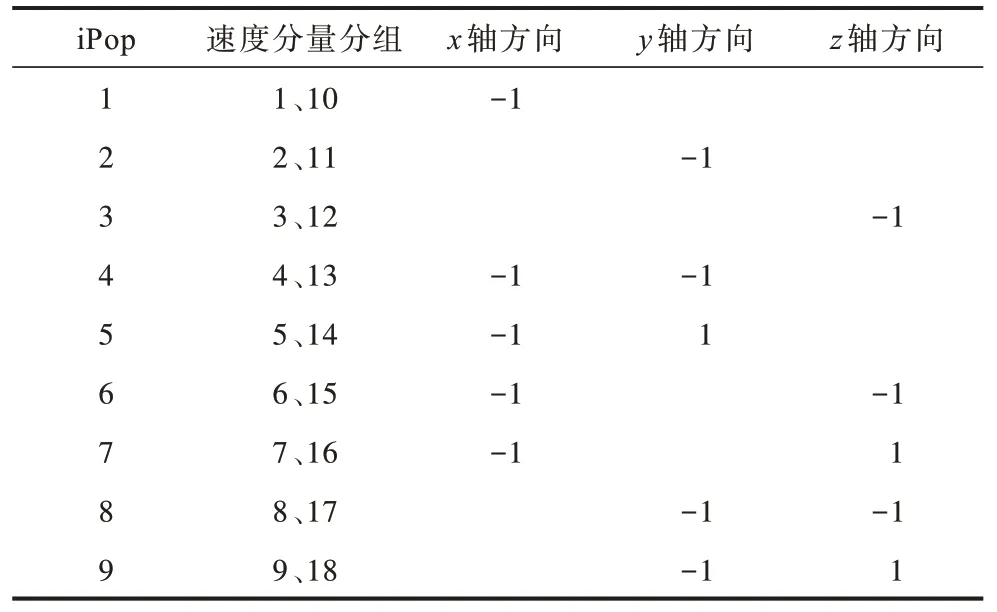
表2 数据交换方向与速度分量的对应关系 Table 2 Correspondence between data exchange direction and velocity component
1.4 并行化存在的难点
由以上分析可知,程序在串行执行时,按照网格的坐标进行遍历,一个格点与周围格点的数据交换会对下一个格点获取的数据产生影响,大部分的格点需要在之前的网格完成计算后才能进行迁移计算。这样就使得迁移计算不能像碰撞计算一样,将每个格点的迁移直接映射到一个计算单元上,使每个格点同时执行迁移计算。
LATT 等[23]在设计Palabos 的GPU 加速算法时也指出:迁移计算不能直接映射到一个格点中,因为存在非本地的数据访问。他们重新设计了算法,并在迭代中增加了用来推导数据来源的全局索引。这样虽然解决了非本地数据的访问问题,但是增加了运算成本。因此,设计合理的并行算法使得迁移计算能够映射到每个计算单元上,能够在不增加运算成本的情况下解决迁移计算的数据依赖问题。
2 并行算法设计
2.1 模型降维
D3Q19 模型为三维模型,每个格点有x、y、z3 个下标。通过分析算法1 可知,swap 函数获取相邻格点和当前格点的坐标至少有一个下标是一致的,同时每个位置速度分量进行交换的相邻格点方向固定。因此,可将三维模型转换为二维模型来进行分析。如图4 所示,根据速度分量的方向,三维的数据交换转换为9 种二维数据交换。降低维度一方面使得数据依赖性降低,另一方面也使离散的算法更方便并行。将模型展开成二维后,可以根据速度分量方向来分析迁移计算在各个方向的运算规律。
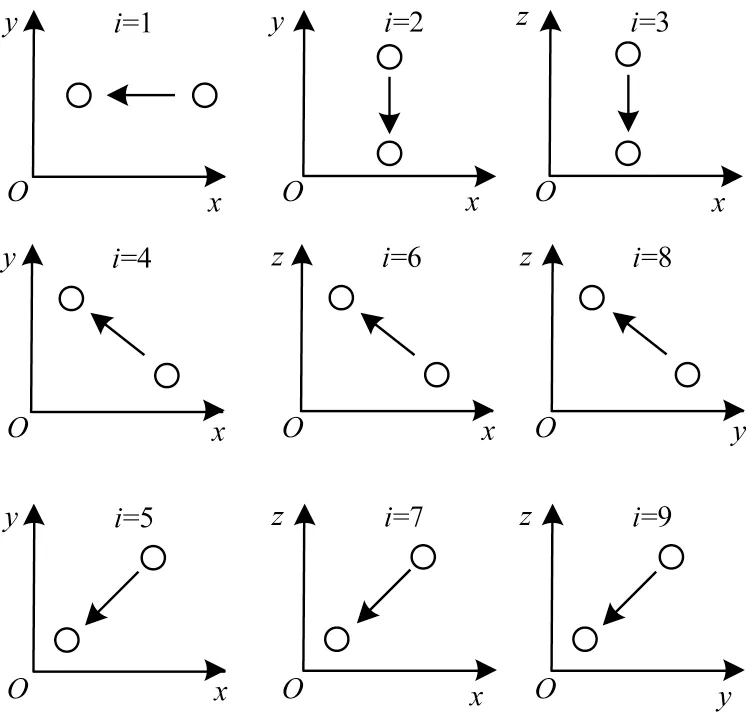
图4 三维模型转换为二维模型的示意图Fig.4 Schematic diagram of converting a three-dimensional model to two-dimensional models
网格中所有格点上固定位置的速度分量都和同方向的相邻格点产生数据交换,例如坐标为x、y、z的格点,与位置1 上的速度分量进行交换的格点坐标为x-1、y、z。因此,相同位置速度分量进行的数据交换都在同一条射线中完成,如图5 所示。图5(a)中射线与轴线平行,对应的速度分量位置为1、2、3;图5(b)中射线与正对角线平行,对应的速度分量位置为4、6、8;图5(c)中射线与正对角线垂直,对应的速度分量位置为5、7、9。在二维模型的情况下,每个格点需要交换的数据只有固定方向上的格点。因此,二维模型数据交换可分解为多个方向一致、平行排列的一维射线。LBM 中流体模型边界格点的碰撞与迁移计算与内部不同,因此,进行优化的迁移计算不包括边界上格点。
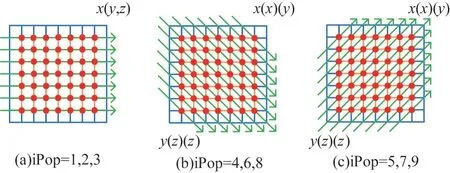
图5 二维模型下交换射线在网格中的排布方式Fig.5 Arrangement mode of exchange rays in grid in a two-dimensional model
通过分析一维模型上的数据交换规律,对整体迁移计算完成前后数据的区别进行对比,可以得到数据的交换规律。
2.2 数据定位
由图5 可知,数据交换的方向有3 种:当方向与轴线平行时,每条射线上参与数据交换的格点数相同;当方向与对角线平行或垂直时,距离对角线越远,参与数据交换的格点数越少。下文分别进行讨论。
2.2.1 方向与轴线平行情况讨论
当数据交换方向与轴线平行,同方向上参与交换的格点数量相同。按照图3 中swap 函数的交换规则,对同一条射线上的多个格点数据进行交换处理,交换方式如图6 所示。从左至右为串行情况下迁移计算的方向,第1 个格点为边界格点,不参与计算,但内部的迁移计算会对边界格点数据产生影响。当参与计算的格点数大于3 时(正常计算时远大于这个值),除了第1、2 个以及最后一个格点,中间部分格点的数据交换方式一致。
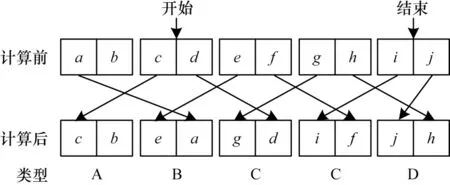
图6 同方向上的格点数大于等于3 时数据的交换方式Fig.6 Data exchange mode when the number of lattice points in the same direction is greater than or equal to 3
按照swap 函数的计算规律,迁移计算完成后同一条射线上所有格点上的数据来源存在4 种不同的类型,如表3 中类型A、B、C、D 所示。

表3 格点数据交换完成后获取到的数据来源 Table 3 Data source obtained after the completion of the lattice point data exchange
2.2.2 方向与对角线平行或垂直情况讨论
当方向与对角线平行或垂直时,大部分的数据交换情况与2.2.1 节中相同,但是存在射线上参与交换的格点数小于3 的情况。针对格点数为1 或2 的情况进行数据交换处理,最终结果如图7 所示。
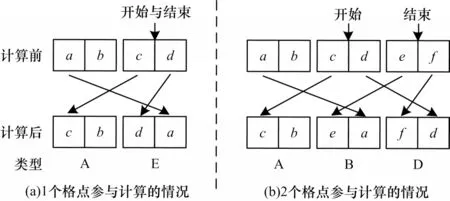
图7 同方向上的格点数为1 或2 时数据的交换方式Fig.7 Data exchange mode when the number of lattice points in the same direction is 1 or 2
按照swap 函数的交换规律,存在一种方式与2.2.1 节中不同,如 表3 中类 型E 所示。
2.3 区域划分
完成数据定位后可以按照图5 中一条射线上的格点数量来对整体网格区域进行划分。例如:当射线上的点大于等于3 个时,射线上第1 个点(包括不在迁移计算区域的边界格点)的交换类型为A,第2 个点为类型B,中间部分的点为类型C,最后一个点为类型D;当射线上的点为2 个时,第1 个点为类型A,第2 个点为类型B,第3 个点为类型D;当射线上的点只有1 个时,第1 个点为类型A,第2 个点为类型E。
将数据的交换类型映射到网格中,每个格点可以通过自身坐标来获取完成迁移计算需要的数据。根据格点的坐标对网格进行区域划分,可以得到速度分量分组下不同数据交换类型的区域。由于在相同射线的排布方式下区域划分的方式一致,因此只列出第一个位置上的映射区域,剩余位置区域划分通过改变坐标可得,结果如表4 所示,其中,N表示网格的长度。

表4 5 种交换类型在整体网格下的映射区域 Table 4 Mapping areas of five exchange types under the global grid
通过模型降维、数据定位和区域划分3 个步骤,可以解决串行计算中存在的数据依赖问题。程序在CPU 端处理完数据后,将数据传输到GPU 端并存储在全局内存中,每个计算核心通过CUDA 模型中的线程和块索引获取格点的坐标,可直接完成碰撞部分的计算。为避免产生访存冲突,需要等待所有计算核心完成碰撞计算后才能开始迁移计算,因此,碰撞计算和迁移计算分为2 个核函数来完成。之后计算核心单元通过2.3 节中区域划分的方式来获取当前格点计算所需要的数据,完成迁移计算任务。
3 并行算法测试与结果分析
3.1 实验环境
本文并行算法的测试在山河超级计算机单节点上完成,节点的相关信息如表5 所示。

表5 测试环境 Table 5 Testing environment
3.2 并行效果对比
对于LBM 算法来说,由于需要大量的迭代计算,因此优化每次迭代的时间消耗能够节省大量的时间成本。根据上文设计的并行算法,测试在128×128×128 规模网格上并行优化的效果,结果显示:原程序的每次迭代平均运行时间在0.36 s 左右,经过优化后时间减少到0.21 s 左右。计算的加速比在1.7 左右,表明了本文设计的并行算法具有可行性。
通过程序在执行时各个部分的计算时间可以了解算法的主要时间消耗,有利于优化的进行。中央处理器(CPU)端可以使用gprof 工具来计算函数的执行时间,而GPU 端可以使用nvprof[24]工具来统计数据传输以及计算时间。在串行版本中,程序完成1×105步的迭代时间消耗在10 h 左右,经过并行优化,CPU-GPU 混合版本的计算时间消耗在5.8 h 左右。图8 展示了CPU 版本和混合版本在128×128×128 网格上单次迭代中各个计算部分的时间消耗对比。从图中可以看出,碰撞和迁移部分在并行后计算时间占比减少,由原本的71%减少到59%。
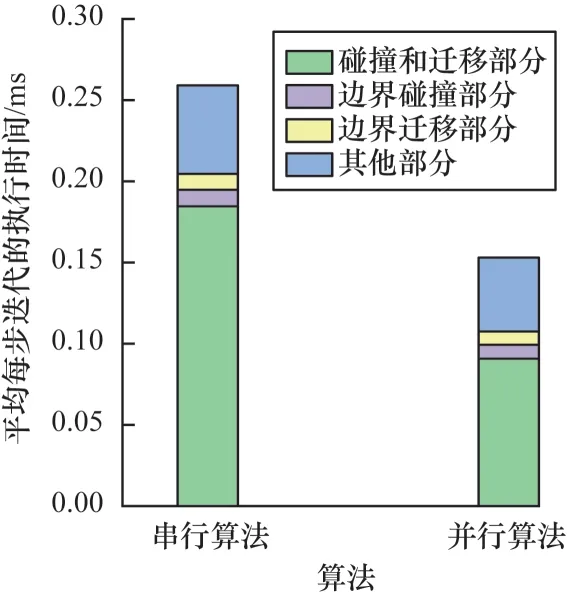
图8 串行算法和并行算法迭代中各个部分的执行时间对比Fig.8 Comparison of execution time of each part in iteration by serial algorithm and parallel algorithm
每秒百万网格更新数(MLUPS)是衡量LBM 算法性能的指标,计算方法如下:
其中:Nx、Ny、Nz分 别为模型中x、y、z轴的长度;I为迭代次数;T为计算时间。MLUPS 指标可反映流体算法的计算效率。如图9 所示,通过对比不同规模下串行计算、只有碰撞部分并行以及本文算法的MLUPS 指标,表明设计的算法提升了流体计算的效率。
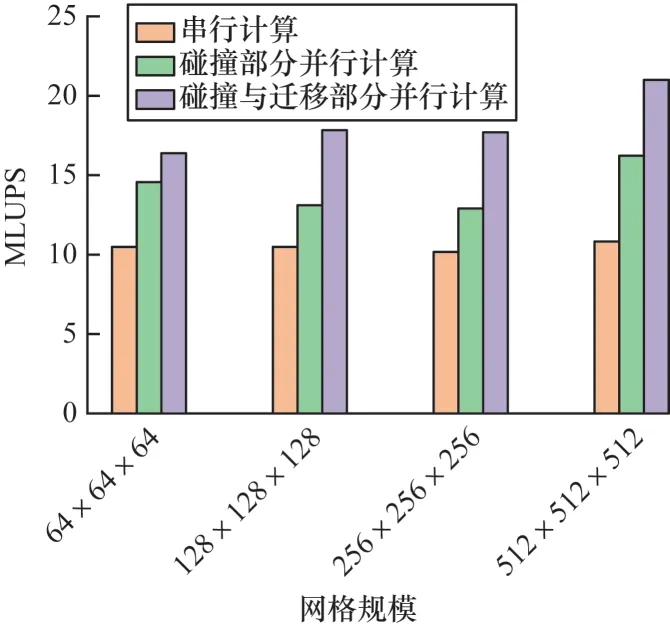
图9 不同网格规模下3 种算法的效率对比Fig.9 Efficiency comparison of three algorithms at different grid scales
3.3 加速比与弱可扩展性
并行算法需要良好的扩展性[25-26],当计算的规模增大时,并行程序仍然需要保持良好的优化效果。针对这一问题,对并行算法进行其他网格维度下的计算测试。同时,对计算的加速比与仅优化碰撞部分的算法进行比较,如图10 所示。
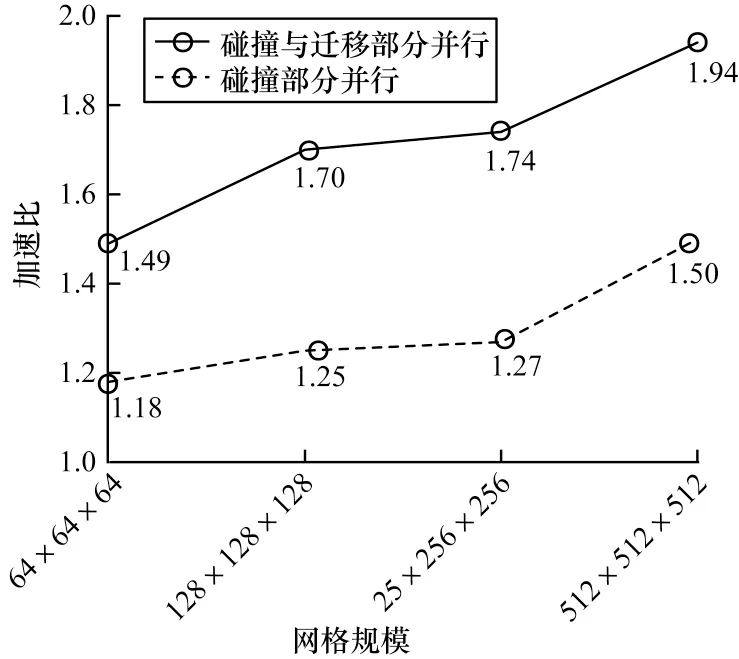
图10 不同网格规模下加速比对比Fig.10 Comparison of acceleration ratios at different grid scales
由图10 可以看出,随着网格规模的扩大,算法的并行效果能保持一定的弱可扩展性。在网格规模为512×512×512 时,具有1.94 的加速比,同时并行算法的计算效率相比于只并行碰撞计算部分的情况提高了30%左右。
4 结束语
随着高速计算机的发展,计算流体力学逐渐成为与理论流体力学、实验流体力学同样重要的研究方向。充分发挥计算机的优势是计算流体力学发展过程中不可或缺的一环,而这正是设计并行算法的意义所在。本文详细分析了LBM 算法中的迁移计算部分在串行计算中的实现逻辑,证明了该部分并行的可行性,然后通过模型降维、数据定位、区域划分等方法,基于CUDA 设计了并行算法。该算法成功解决了迁移计算中存在的数据依赖问题。本文算法是基于单GPU 设计的,因此,下一阶段工作将针对多GPU 的情况对算法进行优化,进一步提高LBM算法的计算效率。
