基于一致性图的权重自适应多视角谱聚类算法
2024-02-29王丽娟邢津萍尹明郝志峰蔡瑞初温雯
王丽娟,邢津萍,尹明,郝志峰,蔡瑞初,温雯
(1.广东工业大学计算机学院,广东 广州 510006;2.广东工业大学自动化学院,广东 广州 510006;3.汕头大学,广东 汕头 515063)
0 引言
多视角数据描述了同一事物在不同视角下的多种数据信息。比如:一个新闻往往以文字、视频、图片等不同的形式出现,一张照片中的景色往往以不同的角度进行拍摄。这些视角的形式、内容通常不同。因此,探索同一对象在每个视角内部隐含的一致性信息是一个极具挑战的问题。多视角聚类是一个有效的数据挖掘算法。其聚类性能依赖于多视角数据一致性信息的发现程度。传统的单视角聚类算法,如文献[1-3]只能依次处理每一个视角,这样做可能会割裂数据内部一致性,无法有效提取多视角内部信息。目前,多视角聚类方法大致可分为基于子空间[4-6]、基于非负矩阵分解[7-8]、基于图[9-10]3 种聚类方法。基于子空间的多视角聚类方法从多个子空间或者潜在空间中学习所有视角数据新的统一表示,以便在构建聚类模型时更容易处理高维多视角数据。文献[11]提出一个协同训练框架下的多视角子空间聚类,利用在一个视角下自动学习的标签来辅助另一个视角下判别性子空间的生成。基于非负矩阵分解的多视角聚类算法利用非负矩阵分解对原始数据进行降维处理,获得的低维数据特征有利于学习数据的潜在特征。文献[12]提出一个将非负特征分解用于数据并将数据进行融合,制定了一个带有归一化策略的联合矩阵分解。基于图的多视角聚类方法利用样本之间的加权无向图来表示样本之间的关系。这一类方法通常假设每个单独的视角都可以捕获数据的部分信息,同时所有的样本关系图都具有相同的潜在一致性数据信息。文献[13]提出一个共同正则化多视角谱聚类方法,在学习共享特征向量的同时减小多个视角之间的差异,保持多个视角之间具有一致性。文献[14]提出学习多个视角间的相似度矩阵,学习得到一个一致性的联通分量的方法。但是,以上这些方法在获取视角间一致性信息时忽略了视角的多样性和重要性排序,平等对待每个视角会受到冗余视角的干扰,无法提取多视角数据内隐含的一致性信息,降低了聚类性能。
本文提出一个基于一致性图的权重自适应多视角谱聚类算法(WGSC)。首先引入自适应的视角权重,使得不同视角发挥不同作用,自适应调节加权视角权重,学习真实的一致性共享相似度矩阵。其次学习具有多样性的特征嵌入,建立特征嵌入与样本嵌入的二部图,实现特征嵌入和样本嵌入之间的特征迁移,最大化两者间的一致性。最后分别将共享相似度矩阵、特征嵌入同样本嵌入联合优化,以此提高样本嵌入的一致性。
1 相关工作
1.1 迁移学习
传统的机器学习通常需要使用同分布假设的标注数据进行训练,然而在实际过程中不同数据集可能存在一些问题,比如数据分布差异、标注数据过期和训练数据过期等问题。为了充分利用标签数据,保证新任务上的模型精度,迁移学习应运而生。迁移学习利用辅助数据集来提高目标数据集的学习性能,其目的是获取源域和学习任务中的知识,以帮助提升目标域中的预测函数的学习。
对于该思想在聚类问题中的应用,文献[15]提出自我学习聚类(STC),在大量无标签辅助数据的帮助下对目标数据进行聚类。STC 扩展了基于信息理论的协同聚类算法[16],假设目标数据集和辅助数据集共享相同的特征聚类。迁移谱聚类(TSC)[17]在此基础之上提出了一种基于类似假设的方法。与基于信息理论的STC 不同,TSC 在建立图的基础上对任务进行聚类。在TSC 的基础上,本文将两个视角延伸到多个视角并改善了只能建立相同特征数视角的二部图约束,即便特征数不同的视角也能建立二部图,实现多视角数据中样本嵌入和特征嵌入之间的迁移学习。
1.2 多视角聚类
在文献[13]提出的协同训练和协同聚类基础上,文献[18-19]提出了多种不同的多视角聚类算法。但是这些算法都忽略了不同视角之间的权重和样本关系学习的问题。文献[14]提出了基于图学习的多视角聚类算法,该算法给出了权重参数,使得不同视角信息具备不同重要性。但是这种算法忽略了权重因子非负的问题,因为一个非负的归一化权重能够减少某一个视角完全决定整个算法的情况,使得视角参数更加可靠。因此,文献[20]提出一种可扩展的多视角聚类方法,该方法给每个视角分配非负的权重,从而避免了因某一视角权重过大而决定整体结果。受到该方法的启发,本文提出视角权重向量,视角权重由相似度矩阵和共享相似度矩阵之间的差异自适应调节,无须再手动调节视角权重参数。通过最小化两者之间的差异,促使共享相似度矩阵最大化学习视角间的一致性信息。但是,多视角数据样本的信息尚未得到充分利用,为此本文充分学习样本的特征,建立特征嵌入与样本嵌入的联系,将特征嵌入的多样性特征转化为有利于样本嵌入的一致性表达,实现信息的迁移。
2 WGSC 聚类算法
2.1 符号定义
对于具有nv个视角的多视角数据样本X={X1,X2,…,Xnv},其中,Xv∈Rd×n表示第v个视角下的样本数据,d表示的是对应视角下的特征维度,n是样本点的个数。特征嵌入F∈Rn×c,c表示聚类的个数。‖X‖2,1表示2,1 范数,表示2 范数的平方,表示Frobenis 范数的平方。
2.2 相似度矩阵的初始化
相似度矩阵的初始化通常采用高斯核全连接的方式构造相似度矩阵,本文采用式(1)分别初始化每个视角v的相似度矩阵Sv。该式利用样本点之间的距离计算两者之间的相似度sij,并对相似度矩阵施加范数约束,避免某一个样本点对应的相似度向量si中存在只有一个非零值的情况。
其中:εs是调节相似度矩阵的正则化参数。
2.3 WGSC 算法整体流程
WGSC 算法整体流程如图1 所示,首先构建每个视角的相似度矩阵并初始化其对应的视角权重,对两者进行加权求和,最小化共享的相似度矩阵G和多个视角相似度矩阵Sv之间的差异,以此获得所有视角的一致性表达。其次学习每个视角特征嵌入Av并建立与共享样本嵌入F的二部图,迁移多样性数据于样本嵌入和特征嵌入之间,同时最大化特征嵌入与样本嵌入间的一致性约束,实现多个视角间的多样性信息转化为一致性信息。最终以样本嵌入为中间枢纽站,整合共享相似度矩阵、样本嵌入和特征嵌入的统一学习框架。该框架可分为两个部分:一是本文方法的核心,样本嵌入F的学习是从特征嵌入Av和共享相似度矩阵G中学习一致性和多样性信息,提高样本嵌入的一致性;二是为了充分利用原始数据信息,学习共享相似度矩阵G得到一致性样本关系和迁移特征嵌入的多样性信息。通过相似度矩阵Sv和视角权重αv的结合学习,筛选更优的视角,减少不重要信息的干扰,得到一致性相似度矩阵G。从特征嵌入的多样性信息中学习能够补充单一地学习样本关系的不足,学习到的多样性特征信息能够提供更多多视角间的一致性信息,两者相辅相成最终获得更好的多视角聚类结果。
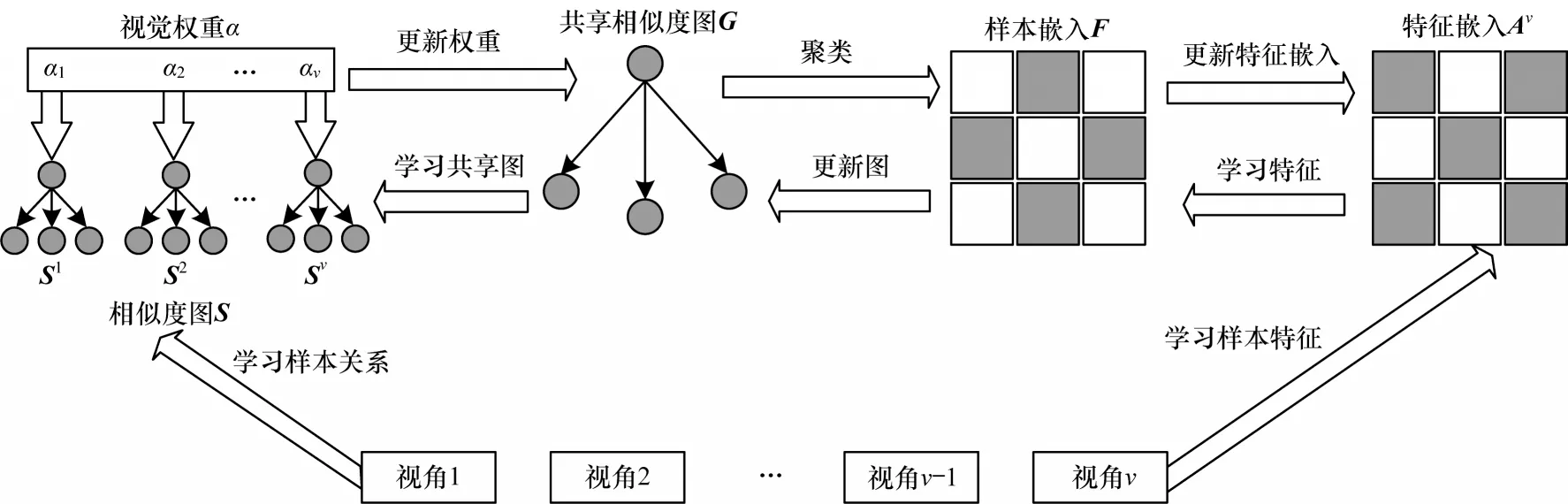
图1 WGSC 算法流程Fig.1 Procedure of WGSC algorithm
2.4 共享相似度矩阵的学习
传统的谱聚类通常预先计算样本点之间的距离得到相似度矩阵。但是,在多视角聚类中,直接对每个视角的相似度矩阵做聚类难以保证多个视角之间的一致性。为了解决这个问题,提出学习视角间共享的相似度矩阵。本文方法赋值相似度矩阵对应的视角权重并对其加权求和,通过Frobenis 范数约束减少加权后的相似度矩阵与共享相似度矩阵的差值,得到具有多个视角间一致性样本关系的共享相似度矩阵。视角权重的自适应调节数值由相似度矩阵与共享相似度矩阵之间的差异决定,如果差异过大会减少视角权重的值,从而提高更优视角的权重。参数权重的引入打破了每个视角之间的平等性,对所含信息重要性差异化的多个视角进行排序,降低了次优视角的权重,最小化了每个视角相似度矩阵与共享相似度矩阵的差异,优化了共享相似度矩阵的一致性学习。最后得到共享的相似度矩阵G:
其中:αv为视角权重;Sv为相似度矩阵;G为共享相似度矩阵。
2.5 特征嵌入的学习
在聚类中,同一类中的样本往往有相似的特征分布,并且特征的相似度越高,属于同一类的概率也越大[21]。本文方法利用迁移学习思想,知识从源域迁移映射到目标域,表现为将特征信息迁移到样本信息,学习每个视角的特征嵌入并将相似的信息传递给样本嵌入。在方法实现上,采用二部图来表示样本和特征之间的关系,寻找样本和特征之间的最小切割,最大化两者之间的相同点。其中,2,1 范数[22]能够有效降低样本中的噪声对特征选择的影响。其函数表达式如式(3)所示:
2.6 目标函数
本文方法以样本嵌入F为中心,以共享相似度图G和特征嵌入Av为出发点,在谱聚类中实现对样本嵌入的优化,得到最终的目标函数。首先,学习每个视角所对应的相似度矩阵,并对权重αv平均初始化。其次,在Frobenis 范数的约束下最小化相似度矩阵和共享相似度矩阵的差异,得到最优的共享相似度矩阵。与此同时,建立样本嵌入F与特征嵌入Av之间的二部图,最大化两者的共同性,以此加强样本嵌入的一致性学习,同时通过2,1 范数降低特征嵌入学习过程中噪声对特征选择的影响。在迭代更新中,共享相似度矩阵学习了所有视角的相似度矩阵,视角权重的更新由相似度矩阵和共享相似度矩阵的差异决定,如果单个视角的相似度矩阵与共享相似度矩阵差异很大,意味着该视角的相似度矩阵存在很多与其他视角不一样的数据点,视角权重将自适应降低权重参数的值,同时更重要的视角权值会增加。通过这种方式,最终的共享相似度矩阵学习了所有视角的一致性信息。共享相似度矩阵由每个视角的相似度矩阵、视角参数共同决定,这为谱聚类的学习提供了一个可靠的相似度矩阵。谱聚类不仅需要考虑样本相似度矩阵,还需要考虑特征嵌入学习。为了进一步优化样本嵌入,将多个视角中的多样性特征迁移至样本嵌入中,通过最大化特征嵌入与样本嵌入之间的一致性,补充了样本嵌入中的多样性信息,提升了样本嵌入的准确性和一致性。具体来讲,样本嵌入将具有一致性的样本关系作用于特征嵌入,特征嵌入将优化后的多样性特征反馈给样本嵌入,样本嵌入学习视角间多样性特征信息,以此最大化视角间的一致性信息。最终图学习、谱聚类以及参数更新在统一的框架中联合优化,在谱聚类作用下得到一个具有一致性和准确性的样本嵌入,提高了最终的聚类性能。本文方法的目标损失函数如式(4)所示:
其中:αv为视角权重;Sv为相似度矩阵;G为共享相似度矩阵;Av为特征嵌入;F为样本嵌入;为归一化后的样本数据;λ为样本学习调节参数;μ、β为特征样本参数。
2.7 模型优化
该节对提出的算法进行详细的求解。由于该算法所含变量非凸,本文采用最优交替乘子法(ADMM)[23]对该目标公式进行求解,取得G、F、A的最优解。首先引入辅助变量Q、β,并得到该算法的拉格朗日函数如下:
其中:Yv是拉格朗日乘子;γ是惩罚参数。
更新G,固定其余变量,保留只含有G的项,最终可以得到式(6):
式(11)为非凸函数,采用最优交替乘子法取得最优解。
更新F,固定其余变量:
定 理1对于秩 为p的矩阵Z∈Rn×p,Z在Stiefel Manifold[24]上的投影定义为:
N是半正定矩阵,式(24)是一个二次凸优化问题。本文实验通过经典拉格朗日乘数的方法来有效解决该问题。因此,式(24)优化等价于式(25)优化:
式(29)的优化参考了文献[25]算法优化。
2.8 算法复杂度分析
在WGSC 算法中,假设总迭代次数为m,视角权重更新中的迭代次数为t。WGSC 由3 个子问题组成:更新共享相似度矩阵,迭代优化共享相似度矩阵G,复杂度为O(n2cm+nm2t+m3t);更新样本嵌入F,需要计算其本身和投影,时间复杂度为O(n2c);更新特征嵌入Av,计算的复杂度为O(n2c)。因此,WGSC的复杂度为O(n2cm+nm2t+m3t)。
3 实验结果与分析
本节将验证上述方法的性能,本文实验将在5 个真实的数据集上运行。
3.1 数据集描述和实验环境
3-Sources 数据集来自3 个著名的在线新闻资源:BBC,Reuters,Guardian。该数据集在3 个来源中共报道169 篇,分为6 个主题标签,每篇新闻都有一个主题标签。Yale 数据集包含了15 个人的165 张GIF 格式的灰度图像,每个对象在不同心情、不同条件下提供11 张照片。MSRCV1 数据集包含240 张图像和8 个对象类别,选择7 种类别的数据,每种类型有6 种提取方式,即CENT、CMT、GIST、HOG、LBP、SIFT。ORL 数据集包含40 个不同主题的400 张图像,所有图像均在暗光均匀的光线下拍摄,且在不同的时间、不同的光照、不同的面部表情和不同细节下拍摄。COIL20 数据集包含20 个物体的图像,每个物体有72 张不同角度的彩色图像,共1 440 张。本文实验运行于Apple M1 芯片,内存8 GB,MATLAB R2020a 软件。
3.2 实验设置与对比算法
首先对实验数据进行归一化处理,使得所有的样本数据值在[-1,1]之间。对归一化后的样本数据输入到WGSC 算法中得到样本嵌入,并对样本嵌入做K-means 聚类得到最终的实验结果。其中将所有对比算法中近邻参数设置为类的个数,本文实验也设置为类的个数。本文实验将多视角的数据分别依次传输到单视角算法中进行运行,并选取实验结果最好的视角作为最终的实验结果,其余算法均一次性运行所有视角的数据并得到最终的实验结果。所有实验结果均由上述实验方式得到,并在同一数据集下运行30 次得到相应实验结果,计算各评估指标的平均值和标准差。
多视角聚类对比算法如下:
1)谱聚类[26]构建样本的相似度矩阵,距离与边权值成反比。通过对所有数据点组成的图进行切图,让切图后不同的子图间边权重和尽可能得低,而子图内的边权重和尽可能得高,从而达到聚类的目的。优点在于具有能在任意形状的样本空间上聚类且收敛于全局最优解,但是对相似度图的改变和聚类参数的选择非常敏感。
2)可扩展多视角聚类(SFMC)算法[20]。SFMC是一个用于多视角聚类的可扩展和无参数的图形融合框架,以自我监督加权方式寻求跨多个视图兼容的联合图。学习的一致性图和视角参数的自适应相互学习解决了超参数的问题。
3)加权多视图谱聚类(WMSC)算法[27]。根据特征向量对聚类结果的影响,引出寻找一个一致的拉普拉斯矩阵,以及对相似的视图赋予相似的权重来差异化最终的聚类,运用最大典型角的方法来衡量聚类结果的差异。
4)聚合相似度矩阵的谱聚类(AASC)算法[28]。对不同视角的相似度矩阵的学习减少不重要特征对聚类的影响,并在此基础之上引入权重向量,优化每个视角的相似度学习。
5)共同正则化谱聚类(Co-Reg)算法[29]。建立一个共同正则化谱聚类框架,并在此基础之上提出两种正则化方案来实现这个目标。两种方案的区别在于K-means 所作用的特征向量的不同,第1 个方案是K-means 作用于所有视图中的其中一个特征向量,第2 个方案是K-means 作用于代表所有视角潜在的具有一致性的特征向量。
6)多视角一致性聚类(MCGC)算法[30]。学习一个最小化所有视角差异的一致性图,并用拉普拉斯矩阵的秩加以约束,最终通过学习到的一致性图直接获得样本的标签。
3.3 结果分析
3.3.1 算法性能对比
本文采用6 个聚类评估标准来评估聚类性能,分别是聚类精确度(Accuracy)、标准化互信息(NMI)[31]、纯度(Purity)、精确率(Precision)、召回率(Recall)和F1 值。这6 个评估标准下的实验结果值越大,表明效果越好。表1~表5 分别展示了本文算法与多个对比算法在3-Sources、MRSCV1、Yale、ORL、COIL20 数据集下的实验结果,其中,实验结果均以平均值(标准差)的形式展示,加粗数字为最优值。
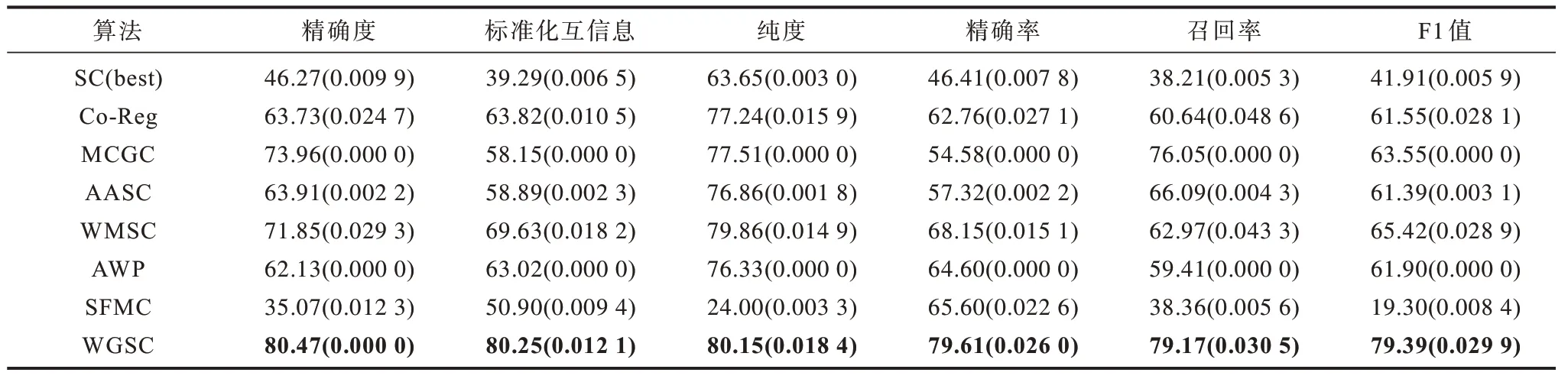
表1 不同算法在3-Sources 数据集上的比较Table 1 Comparison of different algorithms on 3-Sources dataset >%
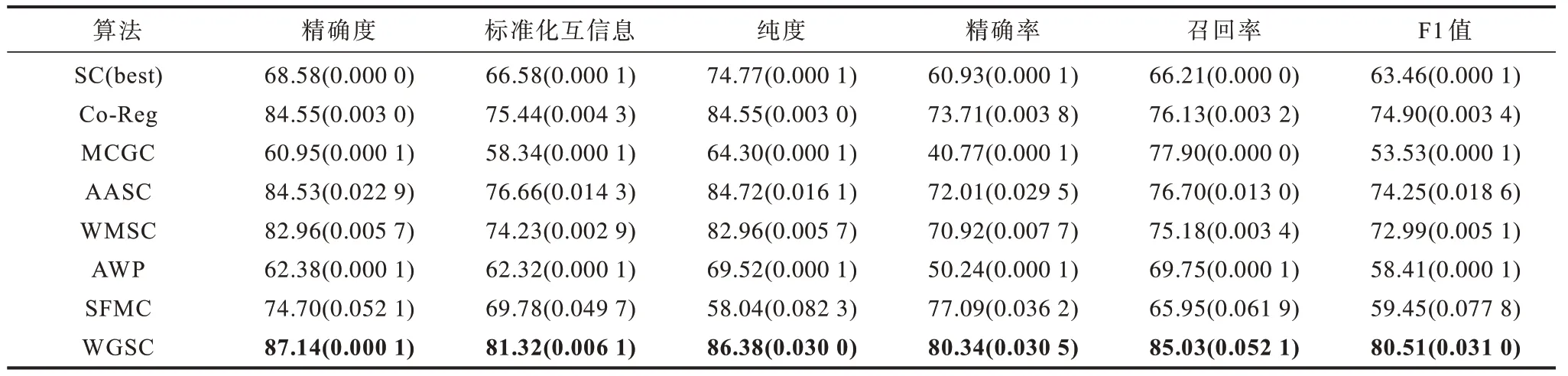
表2 不同算法在MRSCV1 数据集上的比较Table 2 Comparison of different algorithms on MRSCV1 dataset %
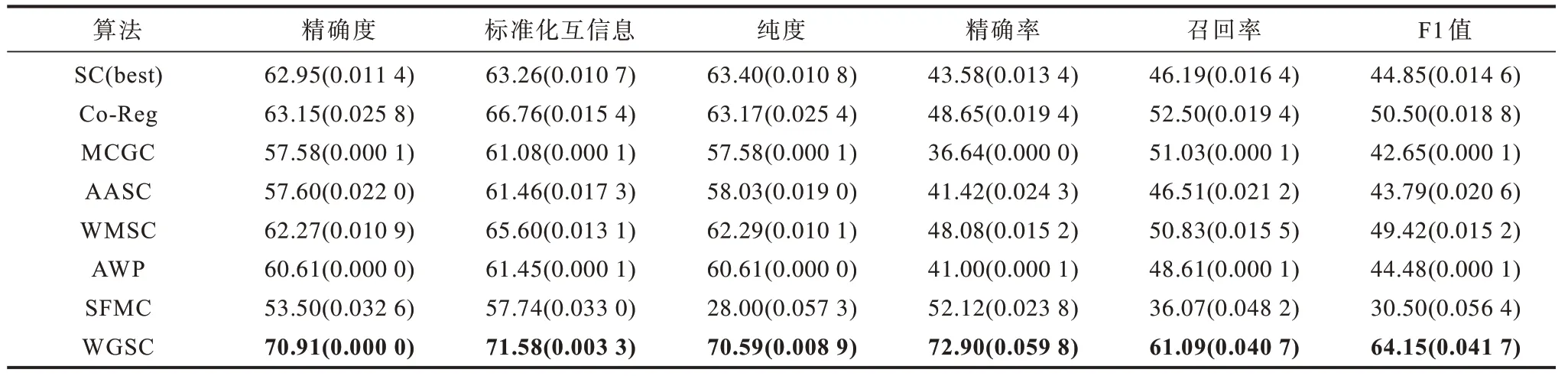
表3 不同算法在Yale 数据集上的比较Table 3 Comparison of different algorithms on Yale dataset %
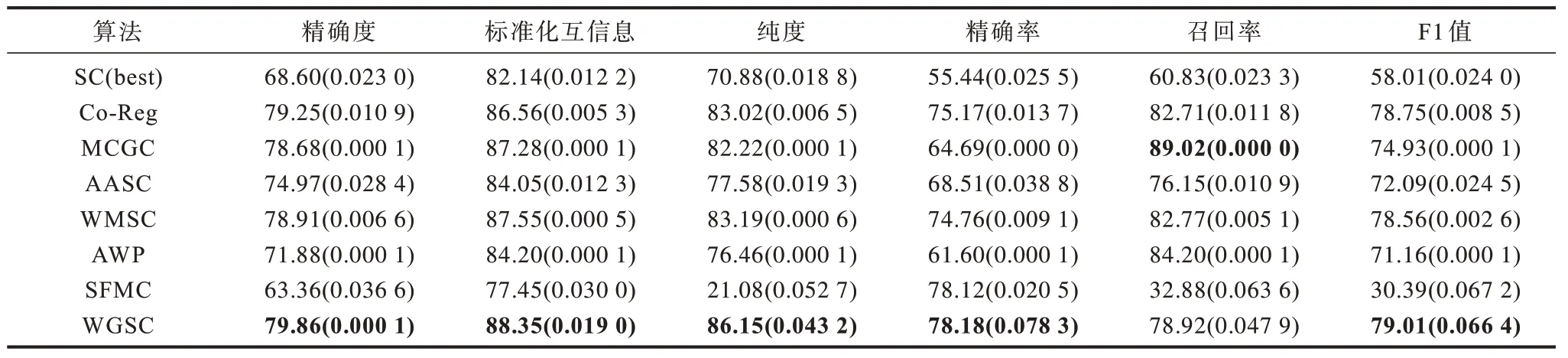
表4 不同算法在ORL 数据集上的比较Table 4 Comparison of different algorithms on ORL dataset %

表5 不同算法在COIL20 数据集上的比较Table 5 Comparison of different algorithms on COIL20 dataset %
1)WGSC 与SFMC 相比,SFMC 更适用于数据规模更大的数据集,其学习每个视角对应的锚点,压缩了数据的规模,学习视角间的一致性图。但是,在锚点降维过程中损失了很多特征,因此本文利用二部图的方式学习样本特征并进行迁移学习至样本嵌入补充多样性。从表1 实验结果可以看出,WGSC优于SFMC,这表明对于数据相似度矩阵在样本特征损失较大的情况下,学习样本特征能提升聚类性能。
2)WMSC 和WGSC 都是聚焦于得到视角间一致的聚类结果。WGSC 采用的是学习一致性相似度矩阵的方法。为了寻找视角间潜在的一致性样本关系,赋予相似度矩阵对应视角权重,融合相似度矩阵得到具有一致性的共享相似度矩阵。两者不同之处在于:WMSC 学习具有一致性的拉普拉斯矩阵,它运用最大典型角的方法来减少不同视角之间的差异。实验结果表明,WGSC 优于WMSC,因为相比于拉普拉斯矩阵的学习,相似度矩阵学习过程中的数据损失更少,聚类性能更佳。
3)WGSC 在所有数据集的聚类结果正确率比AASC 高出了5%以上,这表明WGSC 有良好的聚类性能。AASC 引入了权重向量并由特征值决定权重的大小。不同于AASC,WGSC 用相似度矩阵决定最终权重的大小,并在每轮中迭代更新。WGSC 对权重的评估具有更加丰富的信息,对于数据关系不清晰和杂乱的视角,赋予更低的权重能够降低包含较多噪声的视角对聚类性能的影响。
4)与WGSC 相比,Co-Reg 学习了具有一致性的特征向量,并最小化不同视图间的特征向量之间的差异来达成一致性。不同于Co-Reg,WGSC 直接学习一致性相似度矩阵避免了原始数据中不可靠特征和不重要特征对特征向量的影响。
5)在这5 个数据集中,3-Sources 数据集特征数量远多于样本点个数。因此,特征较多的数据集在WGSC 算法上的表现相比于其他算法表现更佳。这是因为WGSC 将视角间的特征信息迁移到了样本嵌入中,且这些视角的多样性特征能够补充样本关系中存在的不足。此外,3-Sources 数据集的样本点个数较少,对模型的迁移特征部分中二部图的计算更有利,与其他算法相比更具优势,不仅学习了构建的相似度矩阵中的样本关系,还学习了大量的特征信息。
综上,该实验验证了自适应学习视角权重能提高共享相似度矩阵学习的准确率,在保证不同视角之间的一致性以外,学习了原始数据的潜在一致性特征,并通过二部图迁移了不同视角间的多样性信息,确保了聚类的准确率。
3.3.2 共享相似度矩阵的一致性验证
在图2 中,图2(a)~图2(c)分别对应MRSCV1 在3 个视角下的相似度矩阵图,图2(d)表示在迭代优化后得到的共享相似度矩阵。可以看出,最终的共享相似度矩阵整合了视角间的一致性样本关系,学习了样本之间潜在的一致性。因此,WGSC 具备学习一致性共享相似度矩阵的能力。
3.3.3 算法收敛性分析
图3 所示为WGSC 在以上5 个数据集中的收敛情况。从图3 可以看出,WGSC 在每个数据集上都表现出稳定的收敛性,且每次迭代都确保了目标函数值的减少。目标函数收敛到正数或负数,其中负数函数值是因为特征嵌入学习中存在负数项,尤其是原始样本数据相比于其他的项的值更大,所以目标函数值为负数是正常的。一般在30 次之后达到收敛效果,获得了该算法的局部最优值,从而验证了该算法具有良好的收敛性。

图3 WGSC 在3-Sources、MRSCV1、Yale、ORL 和COIL20 数据集上的收敛图Fig.3 The converge drawing of WGSC on 3-Sources,MRSCV1,Yale,ORL and COIL20 datasets
3.3.4 参数分析
本文算法中需要调试的参数有μ、λ、β3 个。首先3 个参数的取值范围均设置为{10-4,10-3,10-2,10-1,100,101,102,103},然后对其中2 个取上述范围,另一个设为0.1,最终得到在3-Sources 数据集的正确率[见 图4(a)~图4(c)]、NMI[见 图4(e)~图4(f)]和Purity[见图4(g)~图4(i)]评估指标的实验结果。从图4 可以看出,β在{10-2,10-1,100}下有较为稳定的性能,λ在{10-3,10-2,10-1,100}下表现出可靠的性能。相对于上述2个参数,μ在该算法中的表现相对敏感。

图4 β、μ、λ 在3-Sources 数据集下的参数分析Fig.4 Parameter analysis of β,μ,λ in 3-Sources dataset
4 结束语
本文对谱聚类的相似度矩阵和样本嵌入重点优化,提出一个基于一致性图的权重自适应多视角谱聚类(WGSC)算法。WGSC 基于自适应的视角权重,学习一个一致的共享相似度矩阵,自适应改变每个视角的相似度矩阵对应权重,提高共享相似度矩阵的一致性。通过构建样本点和样本特征二部图,学习每个视角中的特征信息,获得不同视角的多样性信息,以此提高样本嵌入一致性。本文算法建立样本嵌入、共享相似度矩阵与特征嵌入的关系,实现三者间的信息转化,获得最优的样本嵌入。实验结果表明,本文算法能自适应学习权重参数及最优的相似矩阵,迁移特征嵌入中的信息至样本嵌入,有效提升样本嵌入的一致性和多样性,进而提高聚类结果的准确率。本文算法在大规模样本数据下的性能有较大提升空间,对部分参数较为敏感,下一步将挖掘参数与样本之间的关联,构建无参数聚类模型并优化相似度矩阵学习,将模型运用于大规模数据,避免参数对准确率的影响。
