基于翻转网络的低相关性序列数据预测研究
2024-02-29丁国辉刘宇琪王言开耿施展姜天昊
丁国辉,刘宇琪,王言开,耿施展,姜天昊
(沈阳航空航天大学计算机学院,辽宁 沈阳 110136)
0 引言
时间序列数据预测在序列数据分析领域是一个备受关注的研究热点。在许多应用中,精确的数据预测可以使生产、运营、管理及决策活动更加高效。例如:工业领域对液体泄漏进行预测[1],提前感知损坏点并及时进行整修与补救,更好地避免了工厂损失并降低了对工厂生产效率的影响;风速预测[2]可以为风力发电提供保障;准确的温度预测[3]也能够为人们的衣食住行提供更多保障。此外,在大数据时代,对用户喜好进行预测也很重要,通过用户在应用程序的停留时间来预测用户对于该应用程序的参与度[4],可以更好地推送用户感兴趣的事物,大幅提高用户的体验感。类似的应用都利用多个相似、相关的时间序列变量来预测某个时间序列,即多维时间序列预测。使用与被预测数据具有相关性的数据进行预测,不仅可以避免单维时间序列数据预测的局限性,还可以提高准确率。
目前,针对时间序列数据预测的研究已经取得了一定成果。文献[5-8]利用矩阵画像方法对金融时序数据进行预测,但是因无法获取与其相关性较高的数据,仅考虑预测数据本身,难以获得其他因素对金融数据的影响,导致数据预测结果有较大波动。文献[9]利用长短期记忆(LSTM)-门控循环单元(GRU)联合网络对缺失的海洋数据进行补全,由于与海洋数据相关性高的数据获取难度较高,因此这种补全方法仅考虑了自相关性,没有考虑其他因素对预测结果的影响,存在一定的波动误差。文献[10]利用神经网络随机微分方程的模型对金融数据进行预测,通过数学方法获取时间序列数据中的随机性和非线性关系,但是这种方法仅适用于金融数据,具有一定的局限性。在某些实际应用环境中,相关性较高的数据通常不存在或难以获取,仅使用单维数据进行预测也会受到许多时空因素的影响,从而造成预测结果具有较大的随机性。
针对高相关性数据缺失或难以采集等问题,本文对低相关性多维时序数据预测进行深入研究,提出一种基于注意力翻转网络的低相关性多维数据预测方法。首先,利用皮尔逊系数对大量时间序列数据进行分析,发现总体相关性低的数据具有单点相关性随时间而变化的特点,为了更好地利用这种单点之间的相关性并提高模型效率,引入批处理滑动窗口按时间将数据细分为多个时间片,摆脱时间变化带来的干扰,更好地捕获维度相关性;其次,传统GRU 模型能够控制历史信息,提高了对当前时刻隐层输出的影响,从而导致大量丢弃低相关性样本参数的问题,为此,本文提出一种翻转GRU 网络对低相关性多维数据进行初次过滤,控制多维数据在网络中的传递数量,避免维度变量由于相关性较低而被大量丢弃,从而提高低相关性数据在网络中的存活时间;然后,为了根据相关性来对过滤后的时序参数进行划分,建立面向维度的注意力机制对这些参数分配权重,调整不同维度序列在相关性提取过程中的重要度,细分维度参数间的相关性程度,突出相关性特征;最后,建立一种平方LSTM 网络给分配权重后的数据赋予正负值作为其影响力,分别考虑数据对被预测参数的积极影响和消极影响,更细致地确定相关性对被预测数据的重要性,进一步提高预测结果的准确性。本文将所提注意力翻转网络与传统网络模型LSTM、GRU、循环神经网络(RNN)等进行实验对比,并将所提批处理滑动窗口加入传统模型以证明其有效性。
1 相关工作
数据预测已经成为目前大数据领域的研究热点之一,越来越多的应用开始依靠数据预测,其中,时间序列数据预测是数据预测中比较特别的一个研究分支。根据技术手段的不同,数据预测可以分为基于统计学的方法和基于机器学习(神经网络)的方法。
1.1 基于统计学的数据预测方法
目前存在大量的时间序列数据预测方法,其中最经典的是传统数学统计方法,这种方法主要针对单维时间序列数据,其流程主要包括数据特征分析、参数选择、模型验证优化等。1982 年,美国统计学家ENGLE 提出了自回归条件异方差(ARCH)模型[11],这种模型用于实现多变量异方差的时序数据预测,解决了时序数据的波动性预测问题。数学家BOLLERSLEV 通过对ARCH 的改进,提出了广义自回归条件异方差(GARCH)模型[12],使得自回归条件异方差模型的约束条件进一步放宽。文献[13]提出利用差分操作来保证时间序列数据平稳性的自回归综合移动平均(ARIMA)模型。文献[14]提出带有外生输入的自回归综合移动平均模型。文献[15]提出结合了极限学习机(ELM)和DQNPSO(Deep QNetwork-Based Particle Swarm Optimization)优化器的混合深度强化学习模型,该模型能够准确预测隧道诱导的地面响应频率。文献[16]利用模糊信息颗粒构造颗粒复杂网络,构建金融时间序列波动模型。文献[17]采用指数平滑模型、自回归积分移动平均模型,在状态空间模型框架中结合非线性自回归神经网络,以提高预测的准确性,从而解决经济和金融时间序列中线性与非线性模型的准确诊断问题。文献[18]利用随机森林算法来预测运动员的舞蹈动作,通过特征分析揭示运动员在完成动作时的肌肉协同和节奏感。
以上传统时序数据预测模型大部分都适用于单维时间序列数据,且容易受到非线性因素的干扰。时间序列数据具有很强的复杂性和不确定性,因此,该类模型适用性较低,预测精度很难进一步提升。
1.2 基于神经网络的数据预测方法
近年来,利用机器学习与神经网络进行时间序列数据预测的方法逐渐增多,这种方法首先提取时间序列中的特征,并将其作为标签输入模型,通过建立合适的函数对模型中的参数进行优化,直至达到所需的预测效果。由于时间序列数据大部分都是非平稳数据,存在非线性关系,因此传统的时间序列数据预测模型得到的预测结果在实际应用中存在一定偏差。随着人工智能的不断发展,利用多维时间序列数据对其进行预测的方法越来越受到学者们的关注。
文献[19]提出一种基于卷积神经网络和双向长短期记忆网络的方法对滚动轴承的健康度进行预测。文献[20]为了一次性对所有交通位置进行综合预测,提出一种基于深度元学习的模型ST-MetNet。文献[21]对长短期记忆网络进行改进后与卷积神经网络相结合,构建一种新模型对全网地铁客流进行预测。文献[22]在LSTM 网络中加入新的组块,构建新的网络CTS-LSTM,用于对多维高相关时序数据进行集体预测。文献[23]通过对注意力机制进行深入研究并结合传感器提出一种位置感知注意力机制,然后将位置感知注意力机制与长短期记忆网络相结合,能够动态适应运动轨迹中的局部位置,并通过非固定特征来捕捉位置的显著特征,从而提高预测精度。文献[24]提出一种结合支持向量机回归和卡尔曼滤波的方法,以预测公交车到站时间。
在以上神经网络方法中,使用多维数据进行预测的多维参数都是较易获取的高相关性数据,在多维数据较难获取的情况下都是使用单维数据进行预测,未考虑是否可以使用低相关性数据。因此,本文主要针对低相关性数据进行研究,提出一种针对低相关性数据的预测方法。
2 相关性分析
为了提高预测的精度和可信度,在进行数据预测之前需要对变量进行一定的处理和分析。为了提高模型的收敛速度,首先对数据进行补全和修正,然后对数据进行归一化处理,将每一个数据均收敛到[-1,1]之间。为了更好地理解数据之间的关系,对数据进行相关性分析,发现低相关性数据之间的相关性可以随时间而发生变化,本文基于这个特性建立网络模型,对低相关性数据进行预测。
2.1 时间序列数据
通常来说,一组有限长度的时间序列数据可以表示为从某一时刻(t=1)开始至另一时刻 (t=N)结束的一系列观测数据,即一组时间长度为N的单维时间序列数据可以使用一个1×N的矩阵[xt]1×N表示,具体形式如下:
其中:[x]T表示矩阵x的转置;xt表示t时刻的观测值;N表示此段时间序列数据的长度。
对于时间长度为N的多维时间序列数据,可以使用一个M×N的矩阵[xt]M×N表示,具体形式如下:
其中:xMt表示t时刻的第M个数据;M表示此数据具有M个参数。
时间序列数据表示出了各个领域系统中对历史行为的客观记录,展现出系统随着时间推移的变化规律与潜在特性。通过对时间序列数据的研究,可以更清晰地显示出各个领域系统的运行模式,进而更迅速地对动态系统进行分析决策。
2.2 数据异常值清理
为了降低模型复杂度与计算量,本文对数据进行补全和修正。拉格朗日方法补全的曲线较为平滑,不易出现抖动状态,因此,本文使用拉格朗日插值法进行数据补全;由于时间序列的数值受周期变化和不规则变动的影响,部分数据起伏较大,移动平均法可以对随机的变异值进行过滤,因此,本文使用移动平均法进行异常值修正。拉格朗日插值法如下:
其中:n表示选取缺失值所在的一段固定时间窗的长度;x表示每个数据对应的索引值;β为权重变量;结果y即为时序数据。移动平均法如下:
其中:x1+x2+x3+…+xn是异常值所在时间点的前n个正常连续的数据之和。
2.3 数据归一化
数据归一化是一种无量纲处理手段,使得物理系统中数值的绝对值变为某种相对值。在数据预测过程中,数据集通常处于不同值域,为了提升模型的收敛速度和精度,使数据特征具有相同的度量尺度,本文使用MinMaxScaler 函数对数据进行归一化处理,使得每一个数值都收敛至[-1,1]之间。MinMaxScaler 函数具体如下:
其中:Xscaler表示归一化后的值;X表示当前需要归一化的值;Xmax(aaxis=0)表示每列中最大值组成的行向量;Xmin(aaxis=0)表示每列中最小值组成的行向量;mmax表示要映射到区间的最大值,默认为1;mmin表示要映射到区间的最小值,默认是0。
2.4 数据相关性分析
数据属性的相关性是指数据的2 个属性之间在某种意义下所存在的规律,其目的在于探索数据间的隐藏相关关系网。皮尔逊相关系数(PCC)将结果P分为几类来分析参数之间的相关性。P值范围通常为[-1,1],若为正相关,P>0;若为负相关,P<0。当|P|>0.95 时即为显著性相关,|P|≥0.8 即为高度相关,0.5 <|P|<0.8 即为中度相关,0.3 ≤|P|<0.5 即为低度相关,|P|<0.3 即为弱相关。
目前大部分数据预测研究的数据相关性都较高,皮尔逊相关系数基本在0.8 以上,但在实际应用中,有些高相关性数据不存在或较难获取,而许多与被预测数据相关性较低的数据可以轻而易举地获取到。以共享单车使用量为例,这类数据无法获取到与之显著性相关的数据,其变化还经常受外界因素的影响,因此,可以使用一些较易获取的完整的自然类数据对共享单车使用量进行预测,其相关性关系如图1 所示,图中参数含义如表1 所示。

表1 共享单车参数意义 Table 1 Meaning of shared bicycle parameters
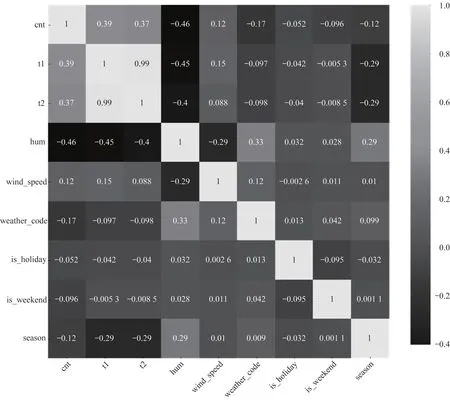
图1 共享单车参数之间的相关性Fig.1 Correlation between shared bicycle parameters
显然,图1 中各个参数对于目标值之间的相关性均为中度相关及以下,各个参数之间相关性也较低,即称为低相关性数据。根据图1 可以看出,气温和体感温度对于共享单车使用量的相关性系数分别为0.39 和0.37,明显为低相关性数据,为了更好地研究数据之间的相关性,本文对这2 种温度与共享单车使用量绘制关系图,结果如图2、图3 所示,阴影部分表示当前温度共享单车使用量的波动范围,实线部分为波动范围的均值。
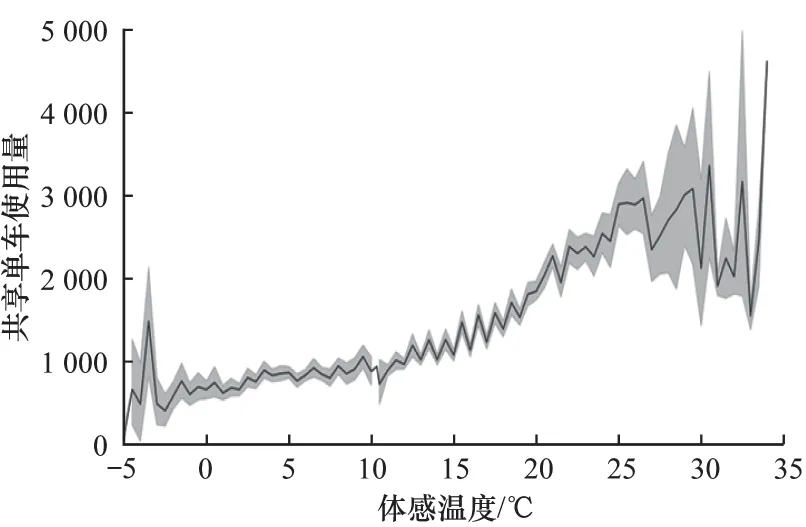
图3 体感温度与共享单车使用量的关系Fig.3 Relationship between body temperature and shared bicycle usage
显然,共享单车使用量波动较大,无法判断当温度上升时共享单车使用量是否必然出现正相关或负相关关系,但当温度达到峰值时,共享单车使用量的波动明显骤减,温度最高时共享单车使用量也达到极值。为了更细致地讨论单点数据之间的相关性,本文选用气温和体感温度最高的10 个点与共享单车使用量进行相关性计算,结果如图4 所示。从图4可以看出,气温与体感温度的相关性有很大提升,分别从0.39、0.37 提升至0.74、0.68,从低度相关提升到了中度相关,低相关性数据存在单点相关性突变的情况。因此,可以得出结论,低相关性时序数据总体相关性较低,但是单点相关性会随着时间的变化而变化,为了获取这种特殊的相关性,本文建立一种利用批处理滑动窗口的注意力翻转神经网络模型,以提高模型对单点相关性的获取能力以及预测精度。
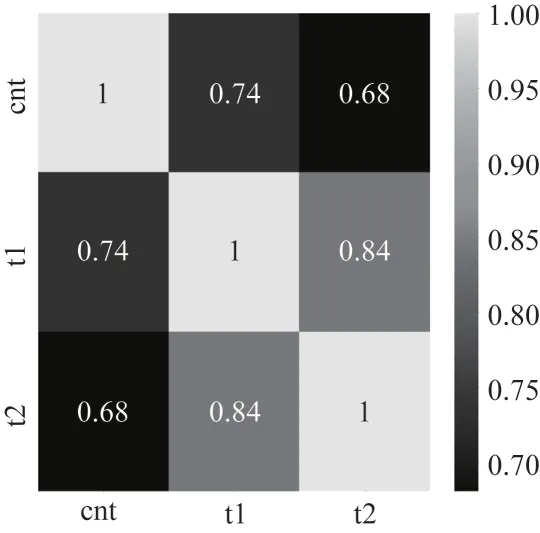
图4 气温与体感温度最高的10 个点与共享单车使用量的相关性Fig.4 Correlation between the ten points with the highest temperature and body temperature and shared bicycle usage
3 注意力翻转网络模型
3.1 批处理滑动窗口
滑动窗口是一种数据处理技术,通过维护一个固定大小的窗口在数据结构中移动,以便有效地处理连续的子序列问题。在通常情况下,滑动窗口算法可以用来解决字符串、数组和链表等数据结构中的问题,例如找到最小值和最大值、计算子数组和平均值以及查找满足特定条件的连续子序列等。
对于多维时序数据预测而言,特征参数较多,数据量较大,若将所有的数据一次性放入模型中,不仅会降低模型效率,还会使网络无法更好地获取数据的前后关系从而影响预测精度。对于低相关性数据而言,一段时间内的数据对于单点的相关性高于总体数据对于单点的相关性,为了更好地利用低相关数据之间的相关性同时提高模型效率,本文提出一种批处理滑动窗口方法,将数据分批后再分为多段并按时间顺序输入模型中。
假设一个单维时间序列为X=(x1,x2,…,xn-1,xn),设输入的长度为h,即窗口长度为h,当前时间点为t,式(6)展示了滑动窗口的滑动公式,图5 展示了滑动窗口的工作原理。

图5 基于滑动窗口的数据集划分机制Fig.5 Dataset partitioning mechanism based on sliding window
为了更好地对数据进行处理,将窗口划分后的数据分成不同批次,将输入的数据流分割成固定大小的块,并沿着时间轴滑动这些块进行处理,这个过程可以在连续、重叠、不同的时间段内进行,以获得更全面的信息。例如,假设有一个包含一周前7 天气温的时间序列数据,可以使用批处理滑动窗口来计算每3 天的平均温度。首先将整个时间序列分割成长度为3 天的块,然后将这些块沿着时间轴滑动,直到覆盖整个时间序列。在每个滑动窗口内,可以计算出3 天的平均温度并输出结果。批处理滑动窗口如图6 所示。
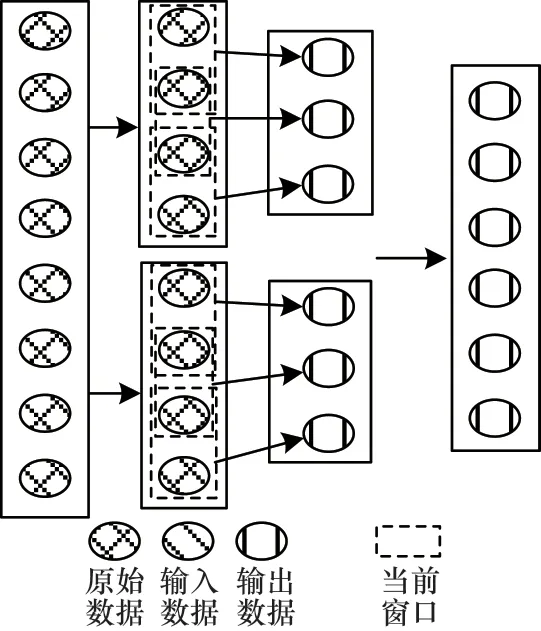
图6 批处理滑动窗口Fig.6 Batch processing sliding window
在批处理滑动窗口建立后,需要设置合适的滑动窗口参数,根据数据集的特点修改滑动窗口参数,可通过时间、季节等特点进行滑动窗口划分,在考虑以上特点的同时,还需结合数据集大小对滑动窗口大小进行调节,使得模型达到最优状态。
3.2 基于维度的注意力机制
受人脑注意力分配的启发,学者们提出了注意力机制,其核心思想是当人在看一种东西时,当前时刻关注的一定是当前正在看的这个东西的某一个部分。换句话说,当人们看向其他位置时,注意力也将随着目光的移动而转移,这意味着当人们处于不同场景时,对场景中不同目标的注意力分布是不同的。
通过对注意力机制进行研究,有研究人员发现注意力机制可以分别添加在时间步和维度上,但核心思想都是对目标数据进行加权变换,通过对输入的不同维度数据进行分析,给予其不同的权重。
对于多维时间序列而言,每个元素的重要性都不同,尤其是对于低相关性数据来说,每个维度对于数据的影响差距较大。本文通过基于维度的注意力机制输入特征,使模型能够自适应地关注相关特征,让各个维度的数据都能体现自身重要性。基于维度的注意力机制通过为不同维度分配不同权重来区分它们的重要性,主要使用Dense 层的Softmax 函数实现权重计算,其计算公式如下:
其中:zi为第i个节点的输出值;C为输入节点的个数。
基于维度的注意力机制模型如图7 所示,其中,(e1,e2,…,en-1,en)为输入序列。使用Softmax 根据相似度值计算出每个隐含层对序列的贡献(S1,S2,…,Sn-1,Sn),为不同维度的数据赋予不同的权重,更好地区分数据之间的相关性,然后将这些权重用于构建向量h',并将h'传递给解码器,向量h'计算如下:

图7 基于维度的注意力机制模型Fig.7 Dimension based attention mechanism model
为了保证模型可以应用到各个场景,分别设计维度权重共享注意力机制和非共享注意力机制。权重共享的注意力机制流程如图8 所示。
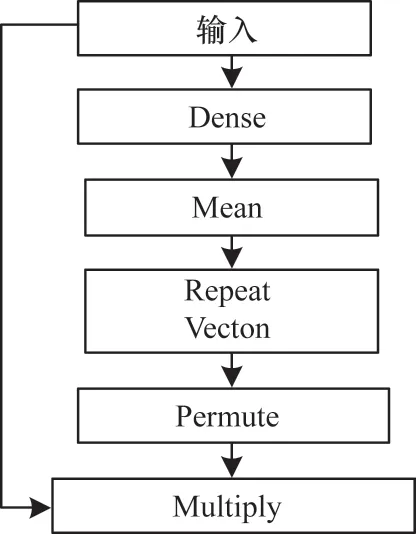
图8 权重共享的注意力机制流程Fig.8 The procedure of attention mechanism with weight sharing
共享权重会导致各个维度的权重相同,无法更好地区分各个维度对于被预测数据的重要性。为了更好地区分各个维度的重要性,本文使用权重非共享的注意力机制进行模型构建。权重非共享的注意力机制流程如图9 所示。

图9 权重非共享的注意力机制流程Fig.9 The procedure of attention mechanism without weight sharing
将整理好的数据通过神经网络初步筛选输入到注意力机制模型中,决定模型需要更多地关注哪一部分的低相关性数据,减少需要处理的信息量,区分低相关性数据之间的重要性,为后续预测工作提供合适的资源。
3.3 翻转网络模型
从第2 节可知,数据的总体相关性较低,但随着时间的变化,数据相关性也会发生变化,因此,数据之间的相关性存在一定的随机性。传统预测模型存在误差较大和优化函数目标单一的局限性,基于指数平滑的预测方法只适用于短期预测,基于支持向量机的预测方法只能获得离散的预测值,无法观测变化趋势,基于循环神经网络的方法只能短期记忆,且极易出现梯度消失的问题,因此,无法促使网络模型学习时间序列相关性之间的随机性,从而导致预测性能下降,尤其是当预测数据所占时间比重较高时,误差积累也会越来越多,严重影响预测性能。
如今在时间序列数据预测方面表现良好的是LSTM 模型和GRU 模型。传统LSTM 模型虽然可以对数据进行长期记忆,但是在长期预测的过程中有陷入局部最优解的可能。传统GRU 模型可以更好地捕捉时间序列中的依赖关系,但是对于长期预测效果较差,会丢失较多数据。对于神经网络来说,长期记忆更容易丢失相对相关性较低的数据,因此,数据单点相关性较高并不足以对下一时刻的数据进行准确预测。为了消减这些问题对模型预测精度的影响,针对传统GRU 网络容易丢弃低相关性样本的问题,本文建立翻转GRU(TURN-GRU)网络,提升相关性较低的多维数据在模型中的存活时间;建立平方LSTM(SQ-LSTM)网络,输入分配权重后的数据,考虑输入数据对被预测参数的积极影响和消极影响,更细致地对输入数据进行影响力划分。
3.3.1 翻转GRU 网络
门控循环单元是一种神经网络架构,主要用于深度学习中的序列建模任务,它是传统循环神经网络的变体,旨在通过门控机制选择性地更新和重制隐藏状态下的信息以解决梯度消失问题。虽然GRU 相比于其他神经网络模型具有较强的长期记忆能力和更少的参数量,但其也具有很多缺点,对于较长的序列,GRU 仍然可能出现梯度消失或梯度爆炸的问题,且GRU 的表达能力受限于其内部结构,因此,在某些复杂任务中需要更深层次、更复杂的架构来提高精度。基于以上问题,本文提出翻转GRU网络——TURN-GRU,其模型整体架构依然沿用传统GRU 的部分网络结构,通过将传统GRU 网络模型整体激活函数进行翻转建立TURN-GRU 网络。
TURN-GRU 的流程为:前一时刻的输出ht-1和当前时刻的输入xt通过tanh 函数分别产生rt和zt,rt与前一时刻的输出ht-1组合通过Sigmoid 函数产生一个新的量,总体决定了有多少数据需要被遗忘;和zt结合生成的值与前一时刻的输出ht-1和zt结合生成的值共同决定当前时刻与过去时刻的数据有多少被保存并输出为当前时刻的ht。TURN-GRU 模型的神经元结构如图10 所示。
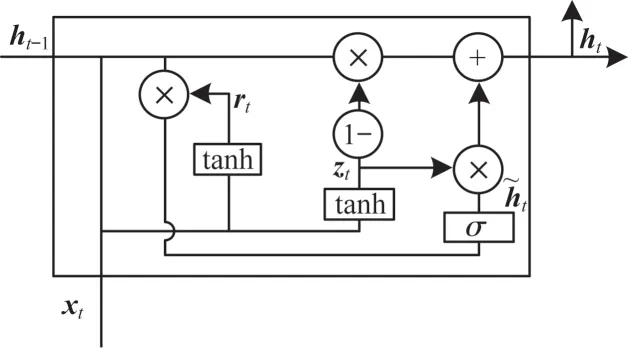
图10 TURN-GRU 的神经元结构Fig.10 The neuronal structure of TURN-GRU
ht-1是上一个时刻的隐藏层输出,ht为当前时刻的隐藏层输出,xt表示当前时刻的输入,σ代表Sigmoid 函数,输出在[0,1]之间,tanh 是双曲正切函数,输出在[-1,1]之间,rt表示当前时刻有多少信息被保留,zt表示上一时刻的数据有多少可以被保留下来,决定有多少数据被遗忘,W表示权重参数。TURN-GRU 计算公式如下:
传统的GRU 网络使用Sigmoid 函数进行数据筛选,让数据经过激活函数后输出在[0,1]之间,提高了数据之间的相关性,但由于低相关性数据之间关联较低,因此筛选后的数据经过Sigmoid 函数会无限趋近于0,久而久之便会被网络彻底丢弃,并且长时间使用Sigmoid 函数会导致饱和,而tanh 函数在一定程度上缓解了神经网络的梯度消失问题,使神经网络的训练更加稳定。为了改善上述问题,本文将传统GRU 模型中所有的Sigmoid 函数均翻转为tanh 函数,同时为了避免模型中的数据冗余,将tanh 函数翻转为Sigmoid 函数,使数据更多地存活在[-1,1]之间,减少Sigmoid 函数在模型中的使用次数和数据无限趋近于0 的可能性,筛选出低相关性数据中相对相关性较高的数据,以此提高数据在模型中的存活时间。
3.3.2 平方LSTM 网络
LSTM 是一种常用于处理序列数据的深度神经网络结构。LSTM 基于门控机制,可以选择性地读取、写入和遗忘信息,包含输入门、遗忘门和输出门以及一个记忆单元,能够根据输入序列和历史信息自适应地控制信息流动,具有良好的记忆能力和长期依赖性。但是,LSTM 过于复杂且需要大量参数,导致训练速度较慢,且这种门控机制会导致梯度消失问题,从而使训练变得困难。在SQ-LSTM 模块中,本文参考传统LSTM 模型的网络结构,删除了标准LSTM 中的输入门,并增加一个“信息门”,通过将输入的数据进行平方计算,将输入的信息均转换为正值,缩小低相关性数据之间的差距,并将网络中的激活函数均转换为tanh,减少参数数量,提高网络模型训练速度,并缓解神经网络中的梯度消失问题。
SQ-LSTM 的流程为:前一时刻的输出ht-1和当前时刻 的输入xt通 过tanh 函 数,分别记 为ft、it、ot。其中:ft旨在为Ct-1提供一个[-1,1]范围内的向量值,控制当前时刻与前一时刻隐藏层数据的保留程度;it平方后可以缩小数据之间的差距,得到信息门的输出,并与前一时刻保留的单元状态共同组成当前的单位状态Ct;ot与当前的单位状态Ct结合生成当前时刻的输出ht。SQ-LSTM 的神经元结构如图11 所示。
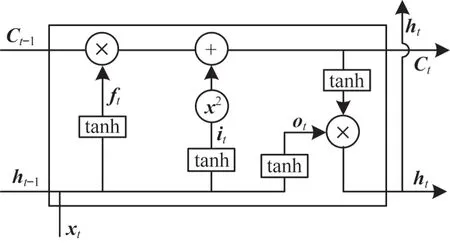
图11 SQ-LSTM 的神经元结构Fig.11 The neuronal structure of SQ-LSTM
ht-1是上一个时刻的隐藏层输出,ht为当前时刻的隐藏层输出,xt表示当前时刻的输入,Ct-1表示上一时刻的细胞状态,Ct表示当前时刻输出的细胞状态,tanh 是双曲正切函数,输出在[-1,1]之间,ft表示当前时刻与前一时刻隐藏层数据保留的输出,it是当前时刻与前一时刻隐藏层数据信息筛选后的输出,ot表示输出门的初始输出,W表示权重参数。SQLSTM 计算公式如下:
模型整体选用tanh 函数使收敛更快,减少迭代次数。此外,tanh 函数将输入为负的数据强制映射为负,分别考虑了数据对被预测参数的积极影响和消极影响,不仅更加有效细致地对数据进行影响力划分,还减少了模型中的参数量,提高了模型运行速度。信息门通过将输入数据平方的方式减小被筛选后的数据信息之间的差距,更好地捕捉数据之间的相关性并保留前后时刻数据的记忆,避免由于数据相关性较低使得数据间差距较大从而导致部分数据被丢弃的问题。
上述2 种模型的建立可以提高之前时刻数据对被预测数据的影响,更好地提升低相关数据之间的关联度,使数据在网络中更具有“话语权”。
3.3.3 注意力翻转网络ATT-TURN-NN
本文提出TURN-GRU 和SQ-LSTM 这2 种网络模型,用于更好地提取数据的相关性并使数据更长时间地保留在网络中。仅使用TURN-GRU 模型可以使数据更好地被筛选并保留在网络中,但其保留的时间较短,仅使用SQ-LSTM 会使网络中模型的数据过多,导致数据冗余,并且文献[25]研究表明单一神经网络模型提取能力较弱,会丢失大量有价值的信息,忽略局部与整体之间的相关性,导致预测结果差别较大且不稳定。因此,为了提升数据在网络中的存活率并对数据进行影响力划分,本文将2 种模型拟合在一起对低相关性数据进行预测。
从第2 节可以看出,数据每一维度针对被预测数据的相关性均不相同,且每一维度的相关性随时间变化的幅度也不同。为了精确每一维度对预测结果的影响,加入基于维度的注意力机制,将基于输入维度的时间注意力机制与翻转网络模型相结合,使网络对于单点相关性投入更多的关注,以获取更多需要关注目标的信息,从而抑制其他无用信息。从后续实验中可以看出,加入注意力机制的模型有更好的拟合效果。
图12 所示为本文所提网络的基本流程,网络主要分为3 个部分,即输入层、隐含层和输出层。其中:输入层包括滑动窗口构建、特征提取等;隐含层为ATT-TURN-NN 网络模型;输出层包括结果输出、结果可视化等。

图12 本文网络基本流程Fig.12 Basic procedure of the network in this paper
按照流程分别设计输入层、隐含层及输出层,具体如下:
1)设计输入层。通过数据归一化、特征提取、数据窗口划分、相关性对比等方法对原始时间序列数据进行分解,获得训练集输入数据、训练集输出数据、测试集输入数据及测试集输出数据。
2)设计隐含层。由于SQ-LSTM 模型参数较多,容易出现过拟合情况,因此首先将处理好的数据通过第1 层TURN-GRU 模型进行初次筛选,提取时间特征。将初次筛选后的数据输入基于维度的注意力机制模型中,为不同维度的数据赋予权重,更好地区分数据之间的相关性。将赋予权重后的数据输入第2 层TURN-GRU 网络模型中并减半神经元个数,再次针对相关性筛选数据,增加权重较高的数据在网络模型中的存活时间。将筛选后的数据输入SQLSTM 模型中,分别考虑数据的积极影响和消极影响,更好地提升模型训练的准确率。通过对神经网络的学习,调整参数使模型达到最佳效果,参数设置如表2 所示。

表2 ATT-TURN-NN 网络参数设置 Table 2 ATT-TURN-NN network parameter settings
3)将测试集输入模型中进行测试,将结果可视化与真实值进行对比,以验证模型的性能。
图13 所示为隐含层ATT-TURN-NN 网络的基本架构。

图13 隐含层ATT-TURN-NN 模型结构Fig.13 Hidden layer ATT-TURN-NN model structure
3.4 模型评估
为了验证所提模型的性能,将其与传统模型进行对比。利用决定系数(R2)[26]、均方误差(MSE)、均方根误差(RMSE)以及平均绝对误差(MAE)4 种指标来评估模型性能。
决定系数一般用于在回归模型中评估预测值和实际值的符合程度,一般R2 越接近1,表示模型效果越好。R2 计算公式如下:
其中:y为真实值;f为预测值;是真实值的平均值。
均方误差指参数估计值和参数值之差平方的期望值,MSE 值越小,说明预测模型有越好的精度。MSE 计算公式如下:
均方根误差为MSE 开平方后的结果,其值越接近0,表示预测值与真实值相差越小。RMSE 计算公式如下:
平均绝对误差表示预测值与观测值之间绝对误差的平均值,计算公式如下:
4 实验结果分析
本文使用英国某城市3 年的共享单车使用量数据来测试模型有效性,实验数据为每小时记录一次,一天记录24 次,每逢整点记录。本次实验使用的数据包括9 个种类,其中,目标值为共享单车使用量,其他参数特征分别为气温、体感温度、湿度、风速、天气、是否为假期、是否为周末以及季节。分别对7 种参数与共享单车使用量进行相关性分析,如第2 节所示。其中,气温、体感温度、风速3 种参数与共享单车使用量呈正相关关系,湿度、天气、是否为假期、是否为周末与共享单车使用量呈负相关关系。根据图1 可以看出,各个参数与共享单车使用量之间的相关性绝对值均低于0.5,属于低相关性时间序列数据。为了更好地利用低相关性对时间序列数据进行预测,本文构建注意力翻转模型,更好地获取低相关性数据之间的关系。
由于数据为多维且数据之间数值差距较大,单位不统一,因此需要先对数据进行预处理,检查数据是否存在缺失,如有缺失就对其进行填补,对填补后的完整数据进行归一化处理,将数据转化为[0,1]之间的范围,更利于计算,提高模型效率,避免因数据差异过大而导致的模型过载问题。
本次实验将80%的数据划分为训练集,20%的数据划分为测试集。为了使滑动窗口在模型中的作用最大化,将滑动窗口长度设置为24,滑动窗口步长设置为1,每次输入数据后移动一个步长,同时产生一个过期数据和一个输出数据,即使用前24 h 的数据预测未来1 h 的数据。将训练数据分为10 个批次进行训练,提高模型效率,对规避低相关性时间序列数据的随机性和间接性具有重要作用。将过大的数据集进行分批处理,可以提高模型的运行速率,降低空间复杂度。
将本文模型与传统模型进行对比,并在不同的参数变化下评估ATT-TURN-NN 模型的性能。首先对不做窗口划分的数据利用部分传统模型进行预测评估,结果如表3、图14 所示。由于数据量较大,图像坐标较为密集,因此选择测试集的前300 个数据进行画图,以确保图像的可视性。分别使用决定系数、均方误差、均方根误差、平均绝对误差来评估模型性能。

表3 未划分滑动窗口时各个模型的评估结果Table 3 Evaluation results of each model without dividing sliding windows
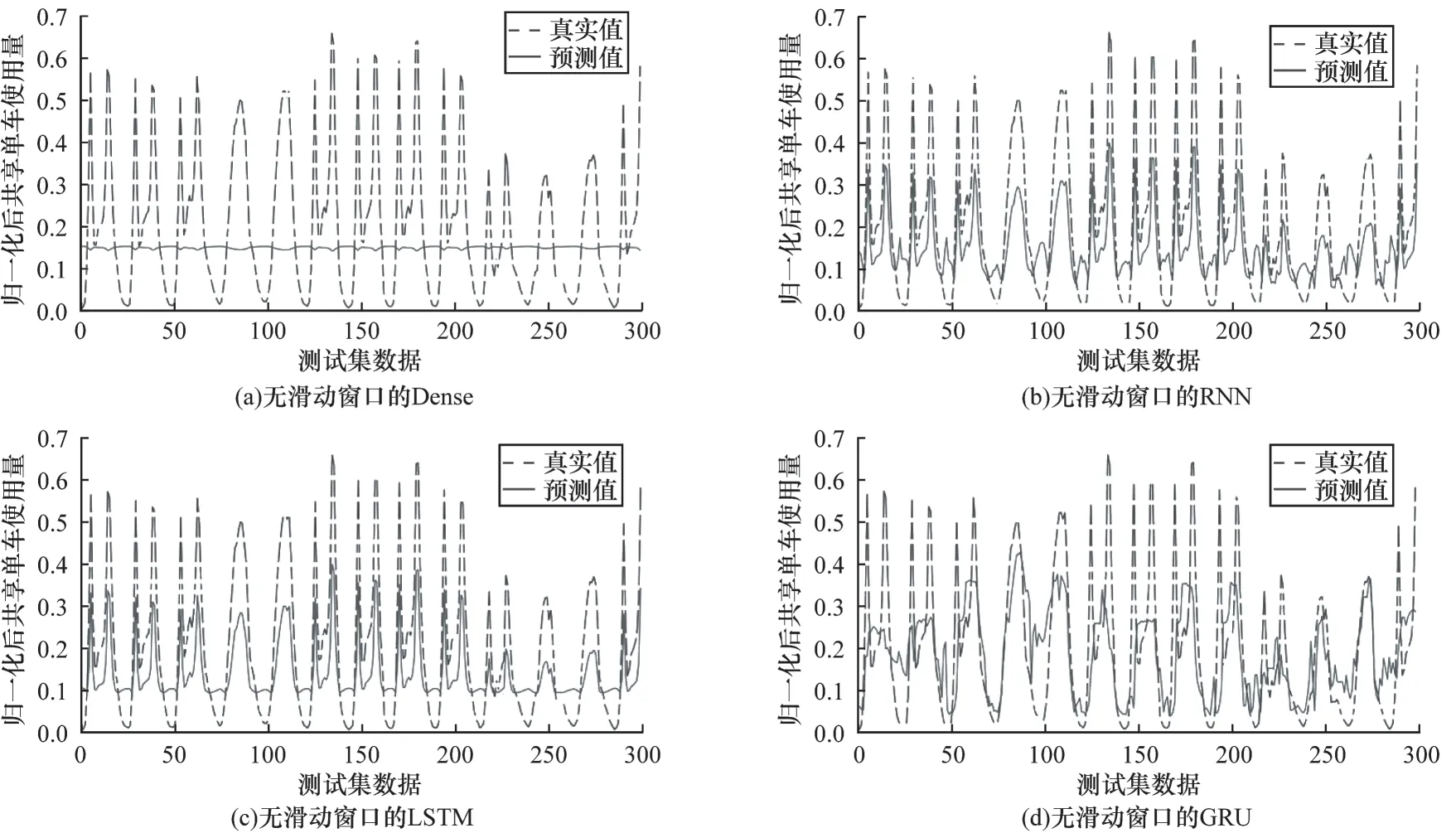
图14 不使用滑动窗口时模型预测值与真实值的对比结果Fig.14 Comparison results between model predicted values and true values without using sliding windows
从表3 可以看出,LSTM 和GRU 相对于RNN 对于低相关性数据预测精度更高,这主要是因为LSTM 网络模型和GRU 网络模型具有记忆功能,可以将之前的数据趋势记录下来并加以利用。从图14 可以看出,传统神经网络模型对于低相关性时序数据处理有明显优势,可以基本看出数据改变的趋势。
分别将全连接网络、LSTM、RNN、GRU、RNN+LSTM、ATT-GRU、ATT-LSTM 与ATT-TURN-NN 模型进行对比,通过实验展示这些模型的预测结果,以验证所提模型的有效性。表4 所示为模型在数据集上的预测结果,图15 所示为上述模型进行滑动窗口划分后预测值与真实值的对比结果。

表4 滑动窗口划分后各个模型的评估结果 Table 4 Evaluation results of each model after sliding window partitioning

图15 滑动窗口划分后模型预测值与真实值的对比结果Fig.15 Comparison results between model predicted values and true values after sliding window partitioning
显然,传统模型[27]对于低相关性数据峰值的预测效果较差,从图14 和图15 中GRU、LSTM、RNN、Dense 的对比可以看出,增加了批处理滑动窗口的神经网络模型具有更好的预测精度。低相关性数据具有单点相关性,批处理滑动窗口可以将一段时间内的数据整合到一起分批输入网络中,以提高数据的相关性。本文还通过实验证明了基于维度的注意力机制的有效性,从图15 和表4 可以看出,增加了注意力机制的LSTM、GRU 和RNN 模型得出的预测值更加接近真实值,证明基于维度的注意力机制可以通过给低相关性数据的不同维度分配不同权重来区分它们在模型中的重要性。最后,为了证明所提注意力翻转模型的有效性,将ATT-TURN-NN 模型与经典模型进行对比,从表4 可以看出,ATT-TURN-NN 模型得出的决定系数最接近1,达到了0.95 以上,证明其得到的预测值与真实值之间差距最小,该模型对于低相关性数据具有较好的预测能力。
表5 所示为各个模型的测试效率对比。从表5可以看出,各个模型测试效率差别不大,效率最高的为Dense 模型,但根据 表3 和表4 可知,Dense 模型预测能力极差,尽管其测试效率较高,但也无法弥补其预测能力差的缺陷。通过表5 可以看出,本文ATTTURN-NN 模型虽然测试效率并未达到最优,但也优于LSTM、GRU、RNN 等大部分模型。结合表3 和表4 可知,本文ATT-TURN-NN 模型可以获得较为准确的预测结果,同时测试效率较高,综上,ATTTURN-NN 模型在处理低相关性时序数据方面优于其他模型。
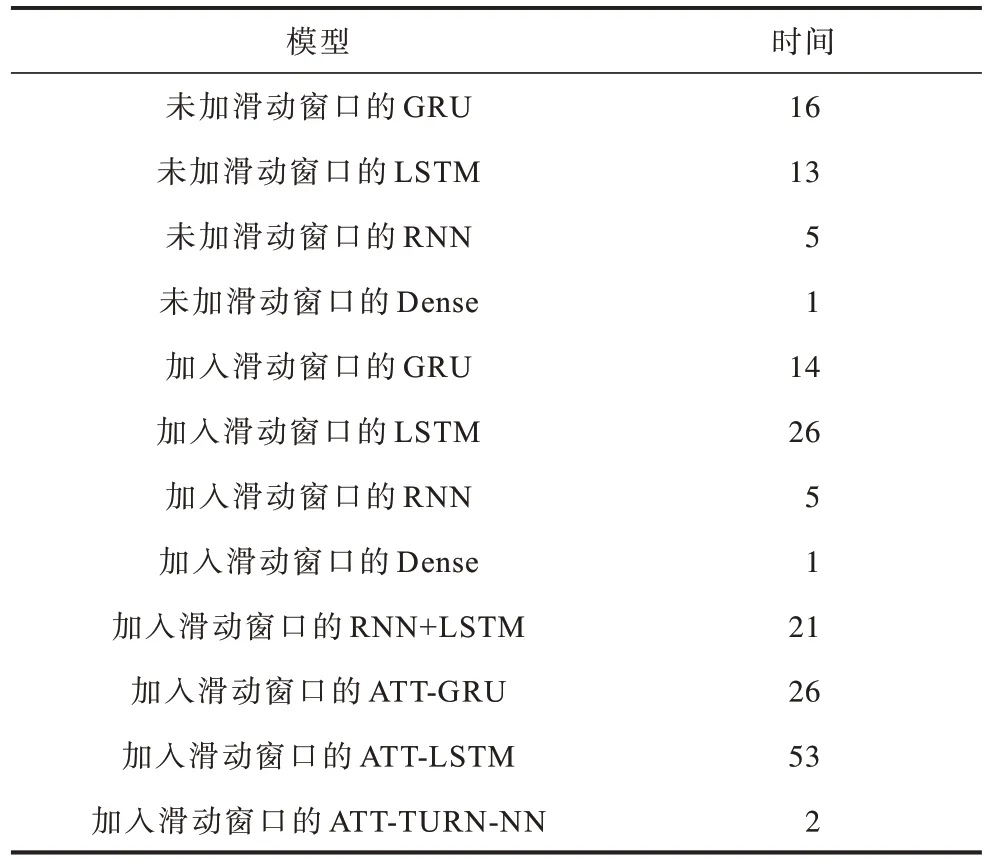
表5 各个模型的时间效率对比Table 5 Comparison of time efficiency among different models 单位:ms
5 结束语
在现实环境中,较难获取高相关性数据,而对单维时间序列数据进行预测时,数据会因为周围环境的影响而产生一定的突变,导致预测结果存在一定的随机性。此外,低相关性数据对预测具有重要意义,维度参数与被预测数据的相关性会随着时间的推移而发生变化,当参数达到某值时其相关性也会随之增高。为了捕捉数据的低相关性,本文提出一种新的混合模型ATT-TURN-NN。将该模型与GRU、LSTM 等传统模型进行对比实验,结果验证了ATT-TURN-NN 模型的有效性。下一步将研究如何更有效地捕捉低相关性数据的相关性,尝试加入空间相关性对低相关性数据进行预测,通过提高数据相关性来提升模型的预测准确率。
