四驱电动汽车变附着路面行驶操稳性控制研究

顾柳恒，张 军

（北京理工大学机械与车辆学院，北京 100081）

1 引言

四轮驱动电动汽车由于具有四轮转矩可按任意比例精确调节、且快速响应的优势，增强了其利用直接横摆力矩控制提高操纵稳定性的能力，因此获得了人们的广泛关注［1］。一般来说，四轮驱动电动汽车的操稳性控制策略通常采用分层控制结构：上层控制器根据驾驶员输入及理想模型计算出期望的动力学参数，再根据反馈的动力学参数计算所需要的广义控制力，即纵向牵引力和附加横摆力矩等；下层控制器负责将广义控制力按照一定的规则，以各驱动电机和制动器驱动/制动等形式分配给四个车轮［2］。

国内外学者都已做过许多有关操纵稳定性控制的研究，文献［3］通过分析质心侧偏角-质心侧偏角速度相图计算车辆极限稳定车速，以车速作为控制开关进行操稳性控制。文献［4］结合了横摆力矩控制与四轮转向，基于滑模控制算法设计控制策略，提高了车辆在高速工况下的操纵稳定性。文献［5］设计了一种基于模糊滑模的控制策略，通过模糊控制理论对变结构增益参数实时调节，削弱了传统滑模控制造成的抖振现象。文献［6］设计了以轮胎利用率和纵向驱动力最优为目标的分配算法，在保证行驶稳定性为前提的条件下尽可能提高车辆的驱动性。文献［7］在转矩分配算法后增加了滑移率模糊控制器，根据滑移率与理想滑移率的差值及变化率计算滑移率调整力矩并附加到最终分配力矩中，避免了滑移率过大导致的失稳现象。传统的控制方法通常采用路面峰值附着系数且将其定义为一个固定值来进行计算，在附着状态良好的情况下，这些控制方法具有良好的控制效果。但当车辆部分或所有车轮处于低附路面，或由于滑移率过大导致附着系数偏离路面峰值附着系数时，传统的控制策略将达不到理想的控制效果，甚至发生失稳的风险。

因此建立考虑路面附着系数影响的四轮驱动电动汽车操纵稳定性控制策略，在上层控制器中充分考虑了附着系数大小对车辆操稳性控制造成的影响，通过判断车辆行驶危险程度决定控制变量的权重；在下层控制器中除考虑附着系数影响外，还集成有滑移率控制算法，当滑移率超出最佳滑移率时加以控制，防止因滑移率过大导致的附着利用率降低。

2 四轮轮毂电机驱动电动汽车操纵稳定性控制策略设计

所提出的四轮轮毂电机驱动电动汽车操稳性控制策略采用分层控制，如图1所示。共分为三层结构，分别为参考模型层、上层控制器和下层控制器。参考模型层根据驾驶员输入，结合车辆的理想模型以及附着状态，计算期望的质心侧偏角、横摆角速度等车辆动力学参数；上层控制器由速度追踪控制器、横摆力矩控制器和滑移率控制器组成，计算广义控制力，即总纵向力、附加横摆力矩以及滑移率调整力矩；下层控制器负责将广义控制力以驱动/制动力矩的形式分配给四个驱动电机和制动器，其中包括以轮胎利用率最优为目标的分配算法和集成滑移率控制的分配算法，按滑移率进行切换。

图1 操纵稳定性控制策略Fig.1 Handing Stability Control Strategy

2.1 参考模型层

为了得到期望的动力学参数，使用理想的线性二自由度模型作为参考模型，即忽略车辆的垂直、侧倾和俯仰运动，只考虑横摆运动和侧向运动两个自由度，并假设纵向速度保持不变，如图2所示。

图2 线性二自由度模型Fig.2 Linear 2-DOF Model

其动力学方程可表示为：

式中：m—整车质量；vx—纵向车速；β—质心侧偏角；γ—横摆角速度；Fyf，Fyr—前轴、后轴侧向力；lf，lr—质心至前后轴距离；Iz—车辆横摆转动惯量；δ—车轮转角。

由于车轮转角较小，令cosδ≈1、sinδ≈0，并假设轮胎处于线性区域内，即轮胎侧偏刚度恒定。此外，由于参考模型层的目的是得到期望的车辆质心侧偏角、横摆角速度的参考值，该参考值可以根据二自由度模型获得。忽略其动态响应过程，令=0、=0，整理出车辆稳态二自由度方程为：

式中：Cf、Cr—前、后轴侧偏刚度；vy—侧向速度。

由二自由度模型推导出质心侧偏角的参考值βd和横摆角速度的参考值γd为：

式中：L—车辆轴距；K—稳定性因数：

考虑到路面附着条件，车辆的横摆角速度应满足的限制为：

式中：μ—路面附着系数。

为保证车辆的可控性，质心侧偏角的限制由经验公式计算得出［8］：

综上，质心侧偏角和横摆角速度的最终期望值βdes、γdes可表示为：

2.2 上层控制器

上层控制器由速度追踪控制器、横摆力矩控制器和滑移率控制器组成，其中速度追踪控制器计算期望的总纵向力，横摆力矩控制器根据当前车辆状态和路面附着条件，计算期望的总附加横摆力矩，滑移率控制器基于各车轮当前滑移率和最佳滑移率，计算各个车轮的滑移率调整力矩。

2.2.1 速度追踪控制

速度追踪控制器的作用是计算车辆所需的总纵向力，采用PID控制，表示为下式：

式中：ev—目标车速与当前车速的偏差；

Fx—计算出的所需总纵向力；

kp、ki、kd—PID控制器参数。

2.2.2 横摆力矩控制

横摆力矩控制器的作用是计算车辆所需的附加横摆力矩，由于车辆的质心侧偏角和横摆角速度相互耦合，追踪单一状态量时无法兼顾车辆的操纵性和稳定性。

因此结合β-dβ相图［9］以及路面附着系数，提出车辆行驶危险程度系数k，实现对质心侧偏角和横摆角速度的分权重控制，同时兼顾操纵性和稳定性，计算出的总附加横摆力矩表示为下式：

式中：M—最终计算出的总附加横摆力矩；Mβ、Mγ—追踪理想质心侧偏角和理想横摆角速度时所需的附加横摆力矩，计算方法和Fx相同，采用PID控制。

k的值由模糊控制器决定，模糊控制的输入为|β+Edβ|和路面附着系数μ，模糊变量设置为NB、NM、NS、Z、PS、PM、PB，表示从负大到正大，分别对应β-dβ相图计算结果X的由大到小，以及路面附着系数的由小到大，模糊逻辑控制规则，如表1所示。

表1 模糊控制规则Tab.1 Fuzzy Control Rules

2.2.3 滑移率控制

车轮滑移率对于路面附着系数、轮胎最大纵向及侧向力有重要的影响，为了提高车辆的行驶稳定性，车轮滑移率应控制在最佳滑移率附近，最佳滑移率受路面附着情况、轮胎侧偏角和车速的影响，可以表示为下式［10］：

式中：sp0—纯直线行驶，车速为64km/h时路面峰值附着系数对应的滑移率，取0.15；α—轮胎侧偏角。

滑移率控制器使用模糊控制算法，控制规则和横摆力矩控制类似，输入为各轮滑移率与最佳滑移率的差值及差值变化率，输出为各轮的调整力矩。

2.3 下层控制器

下层控制器的作用是将上层控制器计算出的广义控制力在满足各种约束的条件下，以驱动/制动力矩的形式，分配到各个车轮驱动电机和制动器，为了提高附着利用率，在下层控制器中设计了两种转矩分配算法，并根据滑移率的大小相互切换，如图3所示。

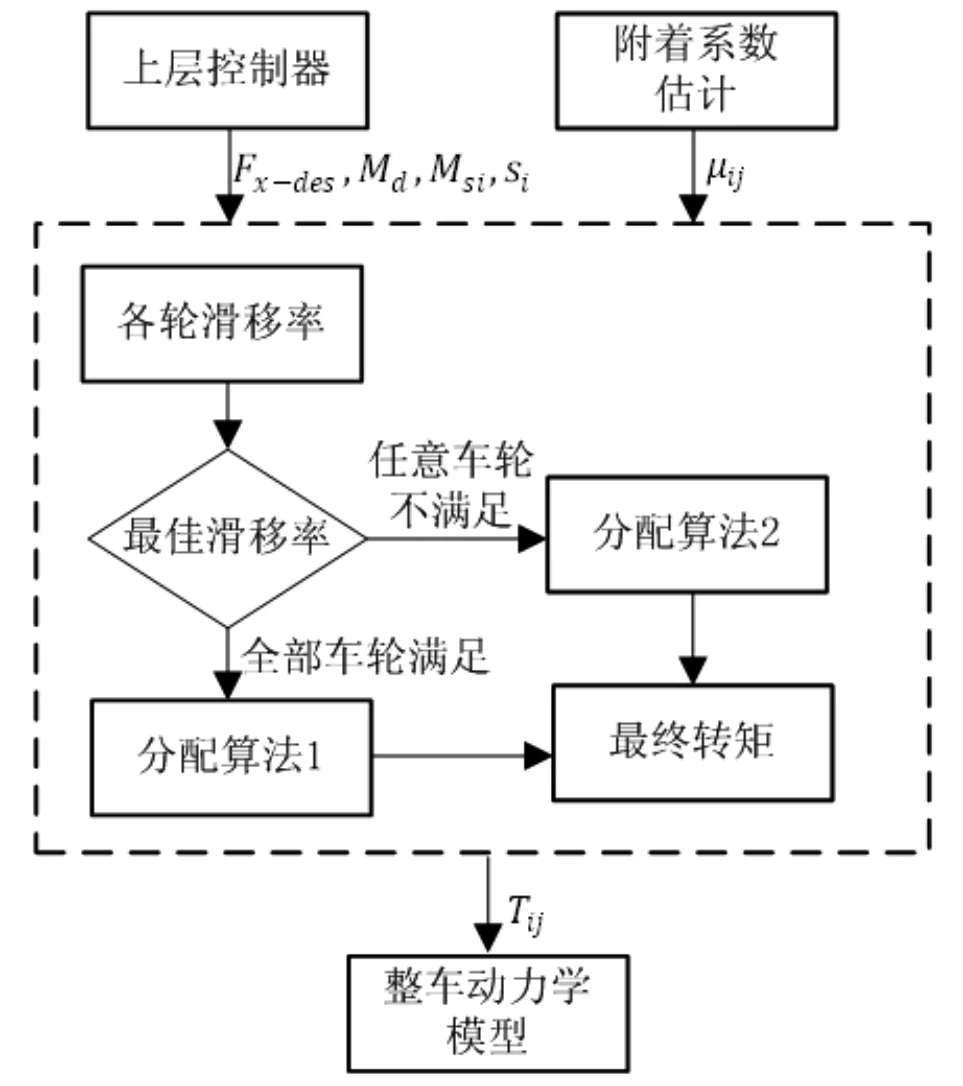
图3 下层控制器策略Fig.3 The Lower Controller Strategy

2.3.1 切换条件

考虑到控制强度与计算复杂度，若全时进行滑移率控制，不利于广义控制力的追踪，且滑移率控制器会影响到控制算法的实时性。因此确定力矩分配算法切换条件：当全部车轮当前滑移率小于最佳滑移率时，采用一般的分配算法，否则采用包括滑移率控制的分配算法，分别称为分配算法1和分配算法2。

2.3.2 分配算法1

第一种分配算法采用最优控制，以四轮轮胎利用率之和作为优化目标，轮胎利用率越小，代表各轮稳定性程度越高：

式中：Fxi—各轮纵向力；Fyi—各轮侧向力；Fzi—各轮垂向力；μi—各轮附着系数；i(i=1，2，3，4)—分别表示左前轮、右前轮、左后轮和右后轮。

分配算法应使实际执行力矩与上层控制器中计算出的广义控制力相符，设置控制目标等式约束如下式：

式中：Fx—期望的纵向力；M—期望的横摆力矩；a—质心至前轴的距离；b—车辆的轮距。

车辆在行驶过程中，轮胎纵向力和侧向力应满足摩擦圆公式，摩擦圆约束表示为不等式的形式：

此外，车轮所能提供的转矩受电机和制动系统输出能力的限制，表示为：

将式（12）、式（13）合并，可表示为如下形式：

同时，为了降低对轮胎侧向力的观测要求，使用HSRI轮胎模型，以轮胎纵向力表示侧向力：

式中：Cαi，Csi—各轮侧向和纵向轮胎刚度，根据魔术公式轮胎模型拟合得出；αi—各轮侧偏角；si—各轮滑移率。

修改不等式约束公式：

修改优化目标如下式：

使用MATLAB非线性优化函数中有效集法进行求解。

2.3.3 分配算法2

第二种分配算法与第一种类似，同样采用最优控制，并在第一种分配算法的基础上增加了滑移率调整力矩，为了减少约束强度，将第一种分配算法中的等式约束以惩罚函数的形式增加到优化目标中，优化目标修改为下式：

式中：ξ—广义控制力的跟踪误差权重系数；

W—纵向力和横摆力矩的控制权重矩阵。

根据附着条件及质心侧偏角调整权重矩阵W的参数，可以兼顾不同行驶工况下的操纵稳定性需求。

第二种分配算法考虑滑移率的控制，当某一车轮的实际滑移率绝对值超出切换条件中规定的最大滑移率绝对值时，该车轮转矩将直接调整为前一时刻的转矩与滑移率控制转矩之和。将其表示为等式约束的形式：

式中：si—滑移率调整开关，当某一车轮滑移率绝对值超出切换条件时，其值为1，否则为0；Fsi—车轮最终输出的纵向力。

不等式约束与第一种分配算法相同，同样使用非线性优化函数进行求解。

3 仿真验证

为验证所设计的控制策略在四轮驱动电动汽车于变附着系数路面行驶时的有效性，包括路面峰值附着系数的变化及各车轮附着利用率的变化，基于Simulink-Carsim 的联合仿真平台设计了对开路面双移线行驶工况对控制策略进行仿真验证。其中左侧道路附着系数为0.2，右侧道路附着系数为0.8，车辆的目标速度设置为100km/h，车辆部分参数，如表2所示。车轮转角，如图4所示。车辆先在右侧高附道路上行驶，转向后，第2.8s左侧车轮进入低附路面，随后第4.2s再次完全进入高附路面。该工况模拟了车辆在变附着系数路面的高速危险行驶状态。为了验证控制策略效果，将所提出的考虑附着系数的操稳性控制策略与传统的转矩平均分配控制策略进行比较，仿真结果，如图5所示。各车轮实时附着系数由无迹卡尔曼滤波算法估计［11］。

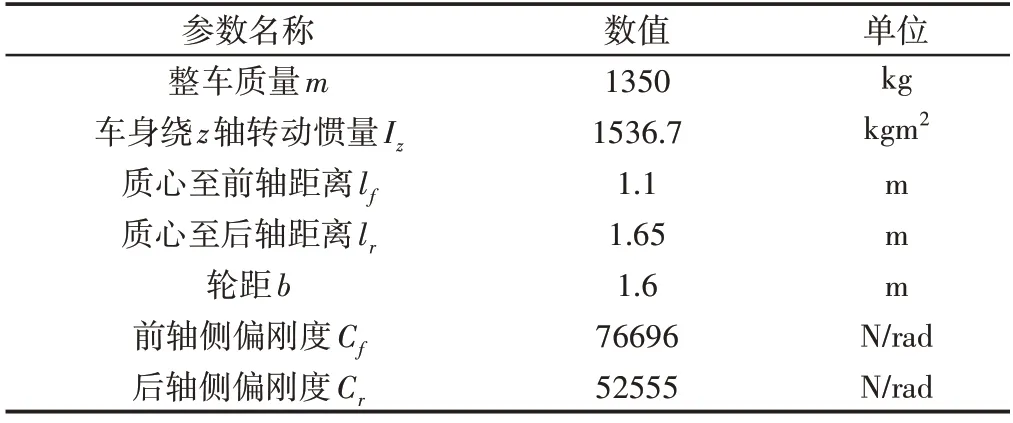
表2 车辆模型部分参数Tab.2 Vehicle Model Partial Parameters

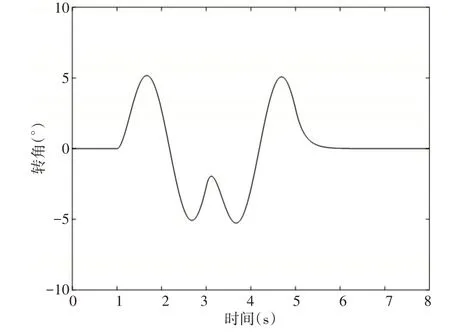
图4 车辆前轮转角Fig.4 Front Wheel Angle of the Vehicle

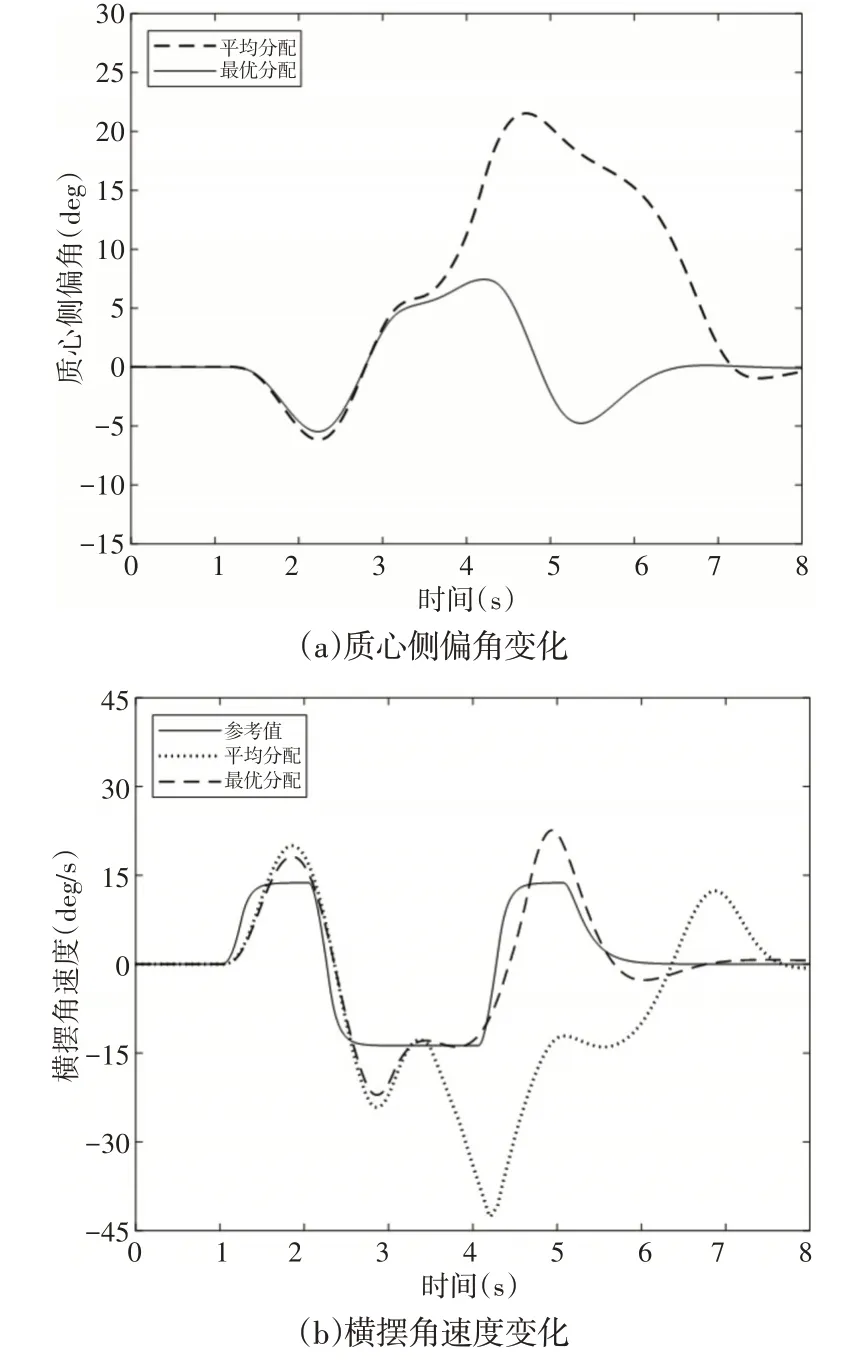
图5 对开路面仿真结果Fig.5 Simulation Results of Split Road Surface

仿真结果表明，当车辆完全行驶在高附路面上时，两种控制策略均能取得良好的控制效果。但当一侧车轮驶入低附路面时，由于平均分配策略没有考虑到附着系数的变化，路面无法提供足够的附着力，车轮滑移率出现较大波动，附着利用率降低，横摆角速度与质心侧偏角出现较大幅值，车辆跑偏失去控制；而所设计的考虑附着系数变化的控制策略将滑移率维持0.11以内，使路面提供的附着系数接近于路面峰值附着系数，仍能保持足够的附着力，横摆角速度基本追踪参考值，质心侧偏角也处于较小的范围内。与平均分配控制策略相比，横摆角速度与参考值之间误差的最大值由26.2°/s下降到8.8°/s，质心侧偏角最大值由22.3°下降到6.8°，整个工况下对横摆角速度和质心侧偏角的控制效果平均提升了33.8%和35.9%。综上所述，所提出的考虑附着系数变化的控制策略能够有效提高车辆行驶的操纵稳定性，从而提高在变附着系数路面行驶时的转向安全性。

4 结束语

针对车辆行驶中各轮附着系数的实时变化，提出了考虑附着系数和附着利用率的分层操纵稳定性控制算法，上层控制器通过PID与模糊控制算法计算了广义控制力和以及滑移率调整力矩，下层控制器基于最优控制，根据最佳滑移率采用两种控制算法集成实现，减小了约束强度。并基于Simulink-Carsim 联合仿真设计对开路面加以验证，仿真结果表明，该策略能够有效约束滑移率维持在最佳范围内，提高了附着利用率，保持横摆角速度基本追踪参考值，同时使质心侧偏角处于较小的区间内，提升了车辆转向行驶时的操纵稳定性。