基于精英引导的改进哈里斯鹰优化算法
2024-02-28李雨恒孟祥宇
李雨恒,高 尚,孟祥宇
(江苏科技大学计算机学院,江苏 镇江 212100)
1 引言
元启发式算法具有原理简单、适用性广、无需梯度信息和避免局部最优能力强的优点,常用于解决传统优化算法难以有效求解的多峰值、不连续和不可微的工程问题[1,2]。群智能算法是一类基于种群的元启发式算法,通过模拟生活在种群中生物的社会行为来在问题空间内随机搜索问题的解。典型的群智能算法有模拟鸟群觅食行为的粒子群优化算法[3],其被广泛应用于大数据背景下的关联规则挖掘[4];有模拟座头鲸捕食行为的鲸鱼优化算法[5],其可用于海上物流配送路径的优化[6]。根据没有免费的午餐定理[7],没有优化算法是通用的最优算法,所以不断有研究人员受到自然现象的启发而提出新的优化算法,这些算法为解决优化问题提供了新的思路和灵感[8]。
哈里斯鹰优化HHO(Harris Hawks Optimization)算法是Heidari等[9]于2019年提出的一种新的群智能算法,算法的主要灵感来源于哈里斯鹰在捕捉猎物时的合作行为及突袭策略。在追逐猎物的过程中,几只合作的哈里斯鹰会从不同方向包围猎物,并根据环境的变化和猎物的逃跑情况选择不同策略来突袭猎物。哈里斯鹰算法具有原理简单、参数少和易实现等优点,但同时也存在收敛精度低、收敛速度慢和易陷入局部最优等缺点。为了改善上述缺点,Li等[10]用精英进化策略来提高算法的收敛速度和跳出局部最优的能力;郭雨鑫等[11]用精英反向学习机制来提升算法全局寻优能力,用黄金正弦算法来增强算法局部开发能力;陈功等[12]用互利共生思想来加快算法收敛速度,用透镜成像反向学习策略提高算法跳出局部最优的能力;汤安迪等[13]用精英等级策略提升算法收敛速度和收敛精度,用高斯随机游走来有效跳出局部最优;朱诚等[14]用趋化校正机制来提高算法收敛精度。上述改进策略都在一定程度上改善了原算法的缺点,但改进算法的性能和鲁棒性仍有一定提升空间。
本文针对哈里斯鹰优化算法存在的问题,提出一种基于精英引导的改进哈里斯鹰优化EHHO(improved Harris Hawks Optimization based on Elite guidance)算法,从3个方面进行改进:(1)引入精英反向学习,生成反向种群与当前种群竞争来增加种群多样性,从而增强算法跳出局部最优的能力;(2)引入精英演化策略,用精英解引导种群进化来提升种群质量,从而增强算法开发能力;(3)引入自适应机制,动态调整开发阶段不同搜索策略的选择概率,从而更好地平衡算法的开发与探索。
2 哈里斯鹰优化算法
HHO算法模拟了哈里斯鹰种群采用不同策略搜寻并捕食猎物的合作狩猎行为,包含探索阶段和开发阶段,并根据猎物逃逸能量的变化实现2个阶段之间的转换。
2.1 探索阶段
探索阶段,哈里斯鹰在搜索空间中以同等概率采用2种策略来搜寻猎物。一种策略是根据种群其他成员和猎物的位置来更新位置;另一种策略是在种群分布范围内随机更新位置,其形式化如式(1)和式(2)所示:
(1)
(2)
其中,X(t+1)和X(t)分别是第t+1次迭代和第t次迭代时哈里斯鹰的位置向量,Xp(t)是第t次迭代时猎物的位置向量,Xr(t)是第t次迭代时哈里斯鹰种群中随机选择的一个哈里斯鹰的位置向量,Xm(t)是第t次迭代时哈里斯鹰种群中所有哈里斯鹰的平均位置向量,r1、r2、r3、r4和q都是(0,1)内的随机数,UB和LB是搜索空间上下界。
2.2 探索阶段和开发阶段的转换
HHO算法根据猎物逃逸能量的大小判断算法是进入探索阶段还是开发阶段,如式(3)所示:
(3)
其中,E是猎物的逃逸能量,E0是初始状态的逃逸能量,t是当前迭代次数,T是最大迭代次数。在HHO算法的每次迭代中,E0在(-1,1)内随机变化。当E≥1时,HHO算法进入探索阶段,哈里斯鹰对猎物进行搜寻;当E<1时,HHO算法进入开发阶段,哈里斯鹰对猎物进行捕食。
2.3 开发阶段
HHO算法使用4种策略来模拟哈里斯鹰捕捉猎物的过程,分别是:软围攻、硬围攻、突袭式软围攻和突袭式硬围攻。猎物总是试图逃离危险环境,用(0,1)内的随机数r表示猎物在哈里斯鹰发动突袭前逃脱的情况:成功逃脱(r<0.5)或逃脱失败(r≥0.5)。
软围攻:当r≥0.5,|E|≥0.5时,猎物逃逸能量充足,并试图通过随机跳跃来误导哈里斯鹰,但未能成功;哈里斯鹰通过软围攻来消耗猎物体力,为后续发动突袭做准备,如式(4)和式(5)所示:
X(t+1)=ΔX(t)-E|JXp(t)-X(t)|
(4)
ΔX(t)=Xp(t)-X(t)
(5)
其中,ΔX(t)是第t次迭代时猎物与哈里斯鹰之间的位置向量之差,J=2(1-r5)是猎物逃逸过程中随机跳跃的强度,r5是(0,1)内的随机数。
硬围攻:当r≥0.5,|E|<0.5时,猎物逃逸能量不足,哈里斯鹰通过硬围攻逼近猎物,为后续发动突袭做准备,如式(6)所示:
X(t+1)=Xp(t)-E|ΔX(t)|
(6)
突袭式软围攻:当r<0.5,|E|≥0.5时,猎物成功逃脱软围攻,且逃逸能量依旧充足,哈里斯鹰通过突袭式软围攻来抓捕猎物,如式(7)~式(9)所示:
Y=Xp(t)-E|JXp(t)-X(t)|
(7)
Z=Y+S×LF(D)
(8)
(9)
其中,D是待求解问题的维度;S是D维向量,每一维都是(0,1)内的随机数;LF(·)是莱维飞行函数;F(·)是适应度函数。
突袭式硬围攻:当r<0.5,|E|<0.5时,猎物成功逃脱硬围攻,但逃逸能量已经不足,哈里斯鹰通过突袭式硬围攻来抓捕猎物,如式(10)~式(12)所示:
(10)
Y=Xp(t)-E|JXp(t)-Xm(t)|
(11)
Z=Y+S×LF(D)
(12)
3 改进的哈里斯鹰优化算法
EHHO算法依旧通过逃逸能量实现探索阶段和开发阶段之间的转换,不同的是EHHO算法在每一轮迭代开始前用精英反向学习对种群位置进行优化,并在开发阶段用精英演化策略替换原开发策略进行种群位置更新,以及通过自适应机制调节精英演化策略中2种不同演化方式的选择概率。
3.1 精英反向学习
反向学习是Tizhoosh[15]于2005年提出的一种新的机器智能的解决方案,通过考虑当前解的反向解来扩大搜索范围,能以更大概率找到更优解。将反向学习策略与群智能算法结合,能有效增加种群多样性和质量,使得算法能够迅速搜索到最优区域。反向解的计算如式(13)所示:
(13)
其中,A、B分别为搜索空间的下界和上界,X为当前解,即反向解与当前解关于搜索空间中心对称。
基本反向学习以搜索空间中心为对称中心进行搜索,虽然扩大了搜索范围,但缺乏针对性,搜索比较盲目,找到更优解的概率仍有待提升。为了增加反向学习找到更优解的概率,本文提出一种精英反向学习方式,以精英中心为对称中心进行反向学习。
基本反向学习中的对称中心始终保持为搜索空间中心,其不随算法迭代动态变化。而精英反向学习中的对称中心为精英中心,其随算法迭代动态变化。精英中心的计算如式(14)所示:
(14)
其中,Xo1、Xo2、Xo3为上一轮迭代时种群中的3个最优解(当前最优解),r为(0,1)内随机数。3个当前最优解蕴含上一轮迭代中最重要的信息,每次反向学习时随机选择一个当前最优解作为精英中心,以充分利用上一轮迭代的搜索成果,增加反向学习成功的机率。
基本反向学习中当前解仅有一个对应的反向解,如果当前种群分布集中,那么其反向种群也会分布集中,这种情况下通过寻找反向解来得到更优解的概率不高。精英反向学习中引入随机参数,使得当前解对应一个反向区域,且该区域的直径为当前解到精英中心的距离。当距离大时,反向学习增强探索能力;当距离小时,反向学习增强开发能力和跳出局部最优的能力。每次反向学习从对应区域中随机生成一个解作为反向解,当反向区域与最优区域有重合时,能增加反向学习成功率。精英反向解的计算如式(15)所示:
(15)
其中,r1、r2均为(0,1)内的随机数,Xc为式(14)所得精英中心。精英反向学习的一个示例如图1所示,该示例为三维空间中通过精英反向学习产生的1 000个反向位置的分布情况。
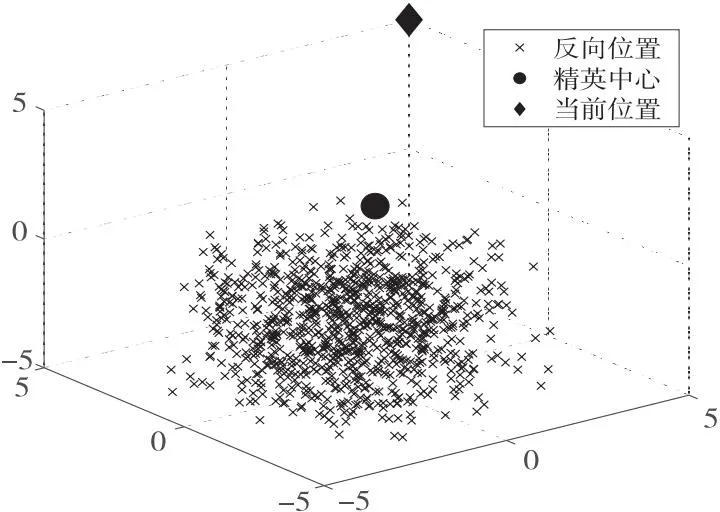
Figure 1 Elite opposite learning图1 精英反向学习
基本反向学习中通过比较当前解及其反向解的适应度值来选择保留更优的那个解,但计算每轮迭代中所有当前解和反向解的适应度值会增加算法的时间开销;此外,如果算法陷入局部最优,在当前解和反向解中优先保留反向解更有可能帮助算法跳出局部最优。
为了尽量减少因反向学习而增加的计算适应度值的次数,同时充分利用反向解跳出局部最优的能力,本文设计一种反向优先策略:先计算反向解的适应度值,如果其小于保留解的历史最优的适应度值,则不再计算当前解的适应度值并直接保留反向解;否则保留当前解并计算其适应度值。保留解计算公式如式(16)所示:
(16)
其中,f(·)为适应度函数,fitness为该保留解迭代过程中的最优适应度值。
3.2 精英演化策略
本文基于进化算法的核心原则,提出一种精英演化策略,以同等概率分别采用2种演化方法来更新种群,充分利用精英解引导种群演化来提升种群质量。精英演化策略保留算法迭代中的3个最优解Xe1、Xe2和Xe3为精英解(历史最优解),且这3个精英解的适应度值满足f(Xe1) ≤f(Xe2) ≤f(Xe3)。
3.2.1 精英交叉演化
精英交叉演化的核心原则是先进行基因交叉再进行基因突变。基因交叉从3条精英染色体获取优秀基因重组成新的染色体;而基因突变则使新的染色体进行小范围的局部变异产生精英交叉演化的染色体。因此,该方法强调开发能力,从而加快算法的收敛速度。该方法包括以下2个步骤:
基因交叉重组以50%的概率分别获取精英染色体Xe2和Xe3的基因来产生新染色体Xc1,然后以(1-p)和p的概率分别获取精英染色体Xe1和Xc1的基因来重组成新染色体Xc2,计算公式如式(17)~式(20)所示:
ip=1-t/T
(17)
p=0.2×r×ip
(18)
Xc1=(0.5⊗Xe2)⊕(0.5⊗Xe3)
(19)
Xc2=[(1-p)⊗Xe1]⊕[p⊗Xc1]
(20)
其中,ip是随迭代次数变化的参数,p是获取不同染色体的基因产生新染色体的概率,⊕表示对染色体进行基因交叉重组,⊗表示进行基因交叉重组的染色体的基因以一定的概率被选择。
基因局部突变使新的染色体Xc2进行小范围的局部变异,以产生精英交叉演化的染色体Xc3,其变异方向与染色体X相关,变异幅度是从高斯分布N(0,0.1)中生成的随机数,计算公式如式(21)所示:
Xc3=Xc2+N1|Xc2-X|
(21)
其中,Xc2是由式(20)得到的新染色体,N1是均值为0、标准差为0.1的高斯分布中的随机数。精英交叉演化的一个示例如图2所示。
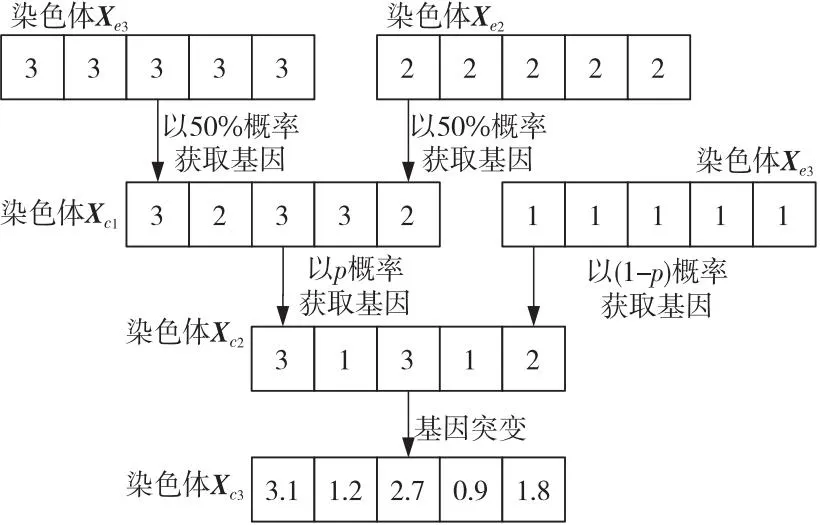
Figure 2 Elite cross evolution图2 精英交叉演化
3.2.2 精英融合演化
精英融合演化的核心原则是先进行基因突变再进行基因融合。基因突变使精英染色体进行较小范围的局部变异产生新的染色体;而基因融合则从精英染色体和新的染色体获取基因片段融合成新的基因,从而产生精英融合演化的染色体。因此,该方法强调探索能力,从而提高算法跳出局部最优的能力。该方法包括以下2个步骤:
基因局部突变使精英染色体Xe1进行较小范围的局部变异,以产生新的染色体Xf1,其变异方向与搜索空间中心CL相关,变异幅度是从高斯分布N(0,1)中生成的随机数,计算公式如式(22)所示:
Xf1=CL+N2|CL-Xe1|
(22)
其中,N2是服从均值为0、标准差为1的高斯分布中的随机数。
基因融合重组使精英染色体Xe1进行小幅度定向变异,使染色体Xf1进行大幅度定向变异,再获取定向变异后的染色体的全部基因产生基因融合重组的染色体,计算公式如式(23)所示:
Xf2=(1+r′1×ip)×Xe1+r′2×ip×Xf1
(23)
其中,r′1和r′2为(-1,1)内的随机数,ip是由式(17)得到的参数,Xf1是由式(22)得到的新染色体。精英融合演化的一个示例如图3所示。

Figure 3 Elite fusion evolution图3 精英融合演化
3.3 自适应机制
精英演化策略包含精英交叉演化和精英融合演化2种演化方式,这2种演化方式在不同情形下具备不同的寻优性能。为了充分地发挥这2种演化方式的寻优性能,本文设计一种自适应机制,通过调整选择概率sp来改变使用2种演化方式进行位置更新的概率。
算法开始迭代时,以同等概率采用2种演化方式更新个体位置,并在每轮迭代开始时判断上轮迭代是否更新历史最优位置,如果更新了历史最优位置,则认为算法未陷入局部最优,不调整选择概率sp;否则认为算法已陷入局部最优,并试图通过调整选择概率sp来改变使用2种演化方式更新个体位置的概率,以寻求提升算法跳出局部最优的可能性,计算公式如式(24)所示:
(24)
其中,选择概率sp是[0,1]内的数,其初始值为0.5;参数n是连续陷入局部最优的迭代轮数;参数diff为上一轮迭代中使用精英交叉演化和精英融合演化更新个体位置的次数之差;如果选择概率sp的值更新后超出[0,1],将其修正为其最接近的边界值,同时将计数器n置0。当算法陷入局部最优时,算法无法直接判断哪种演化方式更适合当前情形,但可推测上一轮迭代中实际使用次数更少的演化方式更有可能帮助算法跳出局部最优,所以增大使用该方法更新个体位置的概率,且增大幅度随算法连续陷入局部最优的迭代轮数的增大而增大。
为了增强探索阶段算法的探索能力,本文对探索阶段更新公式增加随机扰动,使得探索区域更加均衡,以准确找到最优区域。改进后的计算公式如式(25)所示:
X(t+1)=
(25)
其中,r1、r2、r3、r4、r5、r6为(0,1)内随机数,其余参数定义同式(1)。
3.4 EHHO实现步骤
综合上述改进策略,本文所提出的EHHO优化算法伪代码如算法1所示。

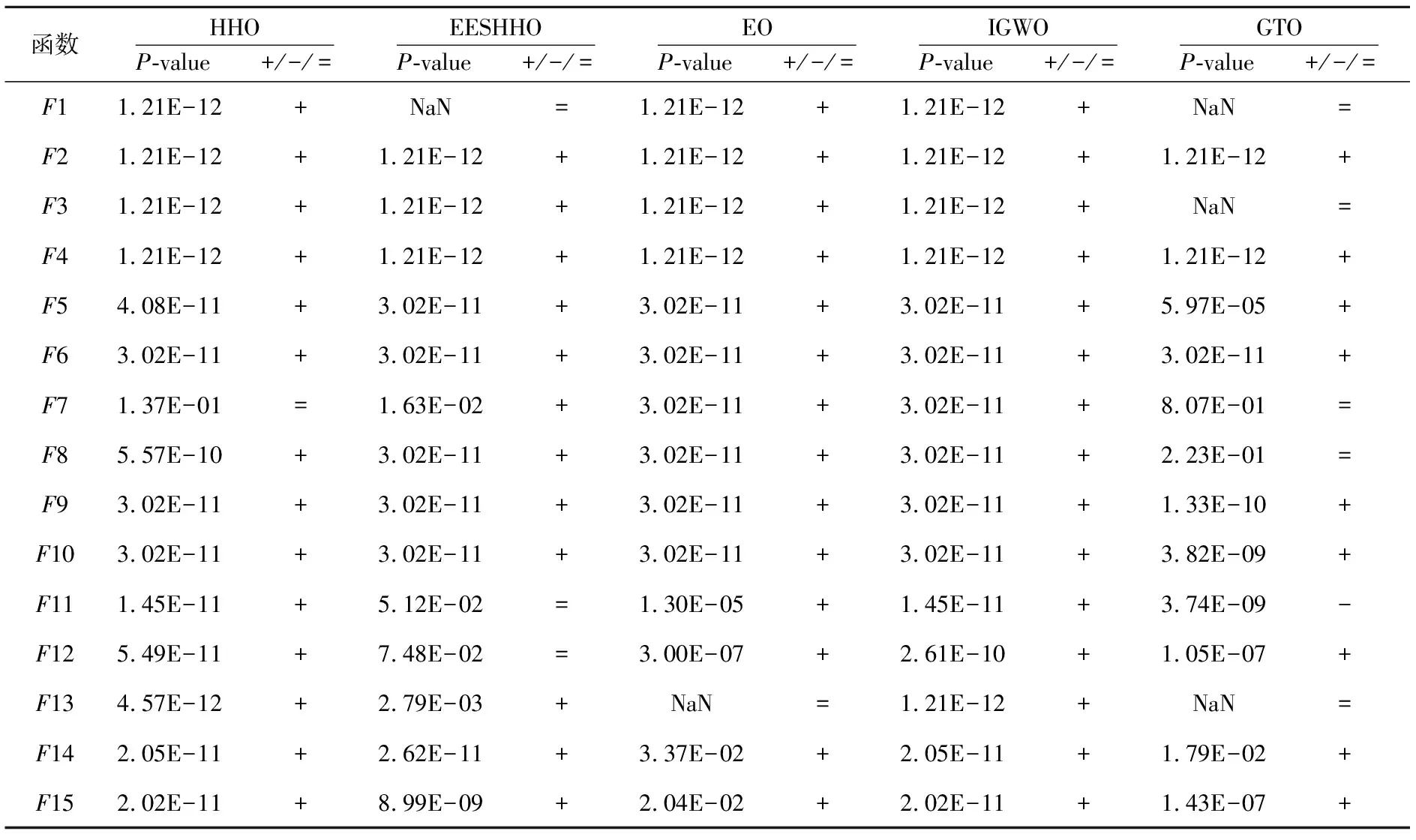
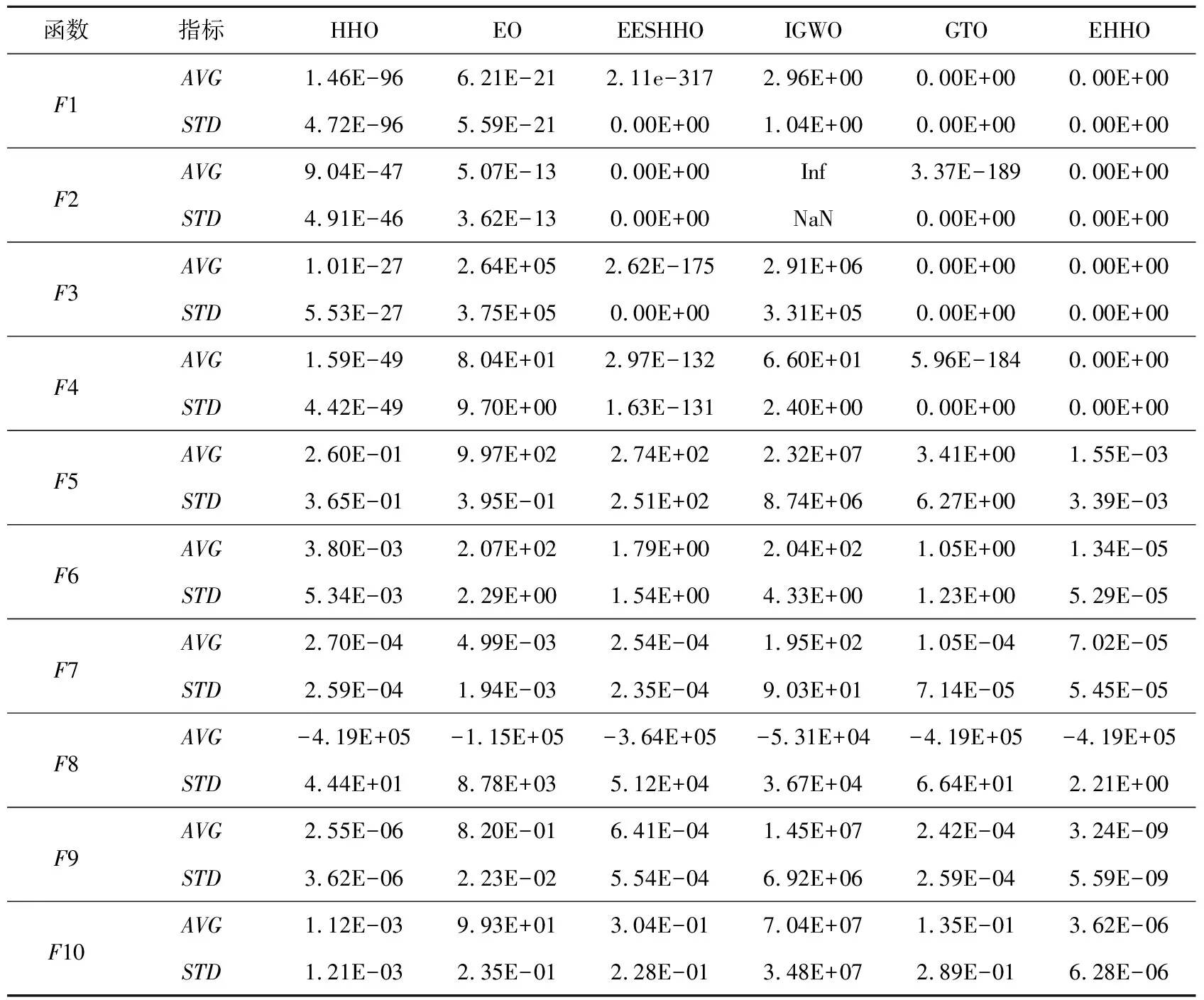
算法1 EHHO算法Input:种群大小N,最大迭代次数T,适应度函数f(·)及相关参数。Output:猎物位置Xe1及其适应度值f(Xe1)。1初始化哈里斯鹰种群位置Xi(i=1,2,3,…,N),历史最优位置Xe1、Xe2、Xe3,当前最优位置Xo1、Xo2、Xo3和选择概率sp;2While (t HHO算法的时间复杂度主要由3个部分组成:初始化、适应度值计算和哈里斯鹰位置更新。当种群数量为N,最大迭代次数为T,问题的维度为D时,初始化的时间复杂度为O(N),计算适应度值并寻找历史最优位置的时间复杂度为O(N×T),哈里斯鹰位置更新的时间复杂度为O(N×T×D)。因此,HHO的时间复杂度为O(N×T×D)。 EHHO算法的时间复杂度主要由5个部分组成:初始化、精英反向学习、适应度值计算、自适应机制运行和哈里斯鹰位置更新。当种群数量为N,最大迭代次数为T,问题的维度为D时,初始化的时间复杂度为O(N),精英反向学习的时间复杂度为O(N×T),计算适应度值并寻找当前最优位置和历史最优位置的时间复杂度为O(N×T),哈里斯鹰位置更新的时间复杂度为O(N×T×D),自适应机制运行的时间复杂度为O(T)。因此,EHHO的时间复杂度为O(N×T×D)。 综上所述,EHHO与HHO的时间复杂度相同,改进策略没有增加算法时间复杂度。 所有仿真实验都在相同环境下进行:实验设备为一台安装Windows 11 64位家庭中文版操作系统的电脑,运行内存为16 GB,处理器为AMD RyzenTM7 5800H 3.2 GHz,测试软件为MATLAB R2020a。所有优化算法均采用相同的公共参数进行测试:种群大小设置为30,最大迭代次数设置为500。为了减少实验中随机因素造成的偏差,所有对比算法在每个测试函数上均独立运行30次,用其寻优结果的平均值(AVG)和标准差(STD)来评估算法寻优性能和稳定性。 为了评估EHHO算法的探索能力、开发能力以及跳出局部最优的能力,本文选取文献[16,17]中的15个基准函数,这组基准函数包括单峰函数和多峰函数。其中,F1~F7为单峰函数,只有一个局部极值,可以揭示不同优化算法的开发能力;F8~F15为多峰函数,具有多个局部极值,可以揭示不同优化算法的探索能力和跳出局部最优的能力。基准函数的相关描述见表1,其中,基准函数F1~F10为维数可变的函数,选取维数d为30和1 000进行测试,基准函数F11~F15为固定维函数。 为了充分验证本文改进策略的有效性,将基本HHO算法与引入精英反向学习的HHO1算法、引入精英演化策略的HHO2算法、引入精英反向学习与精英演化策略的HHO3算法以及引入精英反向学习、精英演化策略与自适应机制的EHHO算法进行对比实验。实验结果如表2所示,其中,函数F1~F7为30维单峰函数,函数F8~F15为30维和固定维多峰函数。 Table 2 Test results of different optimization strategies 由表2可知,对于函数F1,所有改进算法都能稳定收敛到理论最优值;对于函数F2和F4,HHO1算法的收敛精度提升了约150个数量级,HHO2算法的收敛精度提升了约180个数量级,而HHO3算法与EHHO算法能稳定收敛到理论最优值;对于函数F3,HHO1算法的寻优精度提升了约90个数量级,而其余改进算法都能稳定寻找到理论最优值;对于函数F5、F6、F8、F9、F10,所有改进算法的收敛精度都提升了1~6个数量级;对于函数F7和F12,HHO1算法、HHO3算法和EHHO算法的收敛精度都提升了1~2个数量级;对于函数F11,HHO1算法的收敛精度提升了10个数量级,HHO2算法、HHO3算法和EHHO算法的收敛精度都提升了15个数量级;对于函数F13,HHO2算法和HHO3算法的收敛精度提升了10个数量级,EHHO算法能稳定收敛到理论最优值;对于函数F14,HHO3算法的收敛精度提升了11个数量级,EHHO算法的收敛精度提升了14个数量级;对于函数F15,HHO1算法的收敛精度提升了5个数量级,HHO2算法和HHO3算法的收敛精度提升了11个数量级,EHHO算法的收敛精度提升了15个数量级。 综上,引入精英反向学习和引入精英演化策略都能在一定程度上增强算法探索能力、开发能力和跳出局部最优的能力,进而提升算法收敛精度;同时引入精英反向学习和精英演化策略能够融合2种改进策略的优势,对算法性能的提升比单独使用一种策略时更大;而在引入精英反向学习和精英演化策略的同时引入自适应机制能够更进一步提升算法寻优性能和稳定性,即3种改进策略对算法性能的提升均有一定效果。 为了充分验证本文改进算法的有效性,将EHHO算法与其他最新的优化算法进行对比实验,对比算法包括平衡优化算法EO(Equilibrium Optimizer)[18]、模因哈里斯鹰优化EESHHO(Elite Evolution Strategy with Harris Hawks Optimization)算法、改进的灰狼优化算法IGWO(Improved Grey Wolf Optimizer)[19]和人工大猩猩部队优化算法GTO(Gorilla Troops Optimizer)[20]。实验结果如表3所示,其中,函数F1~F7为30维单峰函数,函数F8~F15为30维和固定维多峰函数。 Table 3 Test results of different optimization algorithms 由表3可知,EHHO算法在30维单峰函数上寻优性能优异。对于函数F1,EESHHO算法、GTO算法和EHHO算法都能稳定收敛到理论最优值;对于函数F2和F4,仅EHHO算法能稳定收敛到理论最优值;对于函数F3,仅EHHO算法和GTO算法能收敛到理论最优值;对于函数F5、F6和F7,EHHO算法的收敛精度和稳定性均高于对比算法。 由表3可知,EHHO算法在30维和固定维多峰函数上寻优性能优异。对于函数F8、F9、F10和F12,EHHO算法的收敛精度和稳定性都高于对比算法;对于函数F11,EHHO算法的收敛精度与其他对比算法持平,稳定性比GTO算法略低;对于函数F13,EHHO算法、EO算法、IGWO算法和GTO算法能稳定收敛到理论最优值;对于函数F14,EHHO算法和IGWO算法收敛精度最高,且EHHO算法稳定性高于IGWO算法;对于函数F15,EHHO算法、GTO算法和EESHHO算法收敛精度和稳定性明显高于其他对比算法。 综上,总体上EHHO算法在低维情形下寻优性能良好,收敛精度均不劣于对比算法,稳定性高。 图4a~图4d是对比算法在部分30维单峰函数上独立运行30次的平均收敛曲线。对于函数F1,EHHO算法在约220次迭代时收敛精度达到最高,收敛速度明显快于对比算法;对于函数F4,EHHO算法在约400次迭代时收敛精度达到最高,收敛速度明显快于对比算法,收敛精度比对比算法高100~300个数量级;对于函数F5和F6,EHHO算法在迭代过程中未陷入局部最优,收敛速度快于对比算法,收敛精度比对比算法高3个以上数量级。 Figure 4 Convergence curves of benchmark functions图4 基准函数收敛曲线 图4e~图4h是对比算法在部分30维多峰和固定维多峰函数上独立运行30次的平均收敛曲线。对于函数F8、F14和F15,EHHO算法收敛精度高于或等于对比算法,且收敛速度快于对比算法;对于函数F10,EHHO算法在迭代过程中未陷入局部最优,收敛速度快于对比算法,收敛精度比对比算法高2个以上数量级。 综上,总体上EHHO算法在低维情形下寻优过程顺利,收敛速度快,跳出局部最优的能力强。 为了进一步验证本文改进算法的有效性,在显著性水平P=5%的条件下,本节用Wilcoxon秩和检验来比较EHHO算法与其他群智能算法在15个基准函数上的运行结果之间是否存显著性差异。符号“+”表示EHHO算法优于对比算法;符号“=”表示EHHO算法相当于对比算法;符号“-”表示EHHO算法劣于对比算法;“NaN”表示不适用,无法判定比较数据是否存在显著性差异。 实验结果如表4所示,EHHO算法与HHO算法、EO算法和IGWO算法在14个基准函数上的运行结果存在显著性差异;EHHO算法与EESHHO算法在12个测试函数上的运行结果存在显著性差异;EHHO算法与GTO算法在10个测试函数上的运行结果存在显著性差异。 Table 4 Tests results of Wilcoxon rank sum test 综上,总体上EHHO算法与对比算法存在显著性差异,EHHO算法寻优性能优于对比算法的。 为了进一步验证改进算法的有效性,本节在高维情形下将EHHO算法与HHO算法、EO算法、EESHHO算法、IGWO算法和GTO算法进行对比实验,实验结果如表5所示。 Table 5 Test results in high-dimensional cases(1 000D) 由表5可知,EHHO算法在1 000维单峰和多峰测试函数的测试中,寻优性能与对比算法持平或优于对比算法。对于函数F1和F3,仅EHHO算法和GTO算法能稳定收敛到理论最优值;对于函数F2,仅EHHO算法和EESHHO算法能稳定收敛到理论最优值;对于函数F4,仅EHHO算法能稳定收敛到理论最优值;对于函数F5~F10,EHHO算法在收敛精度和稳定性上都优于对比算法。 综上,EHHO算法在高维情形下仍能保持良好的寻优性能,收敛精度和稳定性均不劣于对比算法。 针对哈里斯鹰优化算法易陷入局部最优和收敛精度低的问题,本文提出一种基于精英引导的改进哈里斯鹰优化算法。引入精英反向学习,以精英中心为对称中心生成反向解,并优先保留反向解以优化种群结构,增强算法跳出局部最优的能力;引入精英演化策略,用精英交叉演化与精英融合演化来更新种群位置,以提升种群质量,增强算法局部开发能力,提升算法收敛精度;引入自适应机制,动态调节选择2种精英演化方法更新种群位置的概率,以增强算法稳定性。选取15个基准函数进行仿真实验,实验结果表明,EHHO算法采取的改进策略都能有效提升算法寻优性能。虽然本文改进策略一定程度上增加了算法的复杂度,但改进后算法收敛速度快、寻优精度高、鲁棒性强,在优化算法中具有明显优势。接下来的研究将考虑如何进一步优化改进算法,将其与实际工程应用相结合。3.5 EHHO时间复杂度分析
4 实验与结果分析
4.1 实验环境与基准函数
4.2 改进策略有效性分析
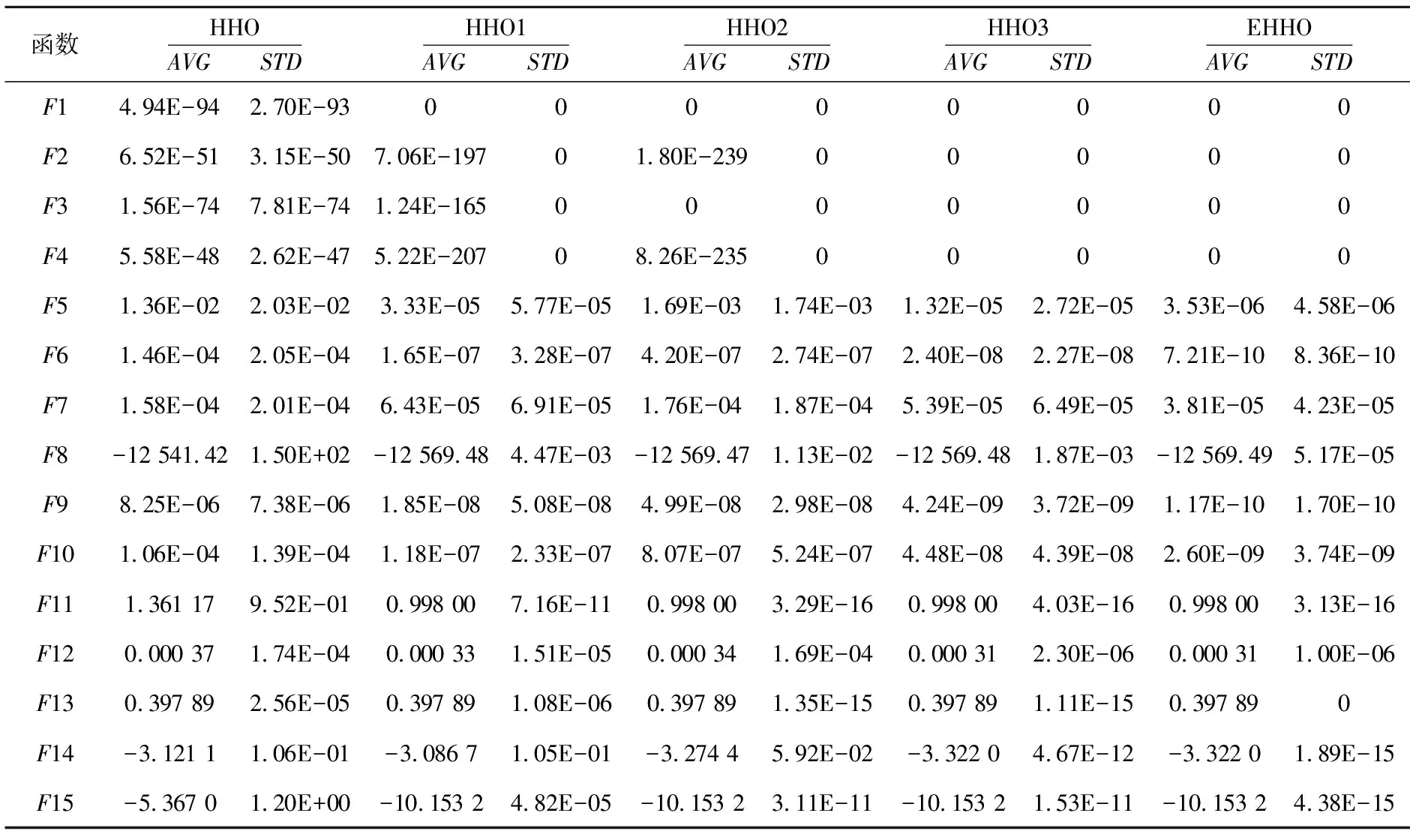
4.3 性能对比分析

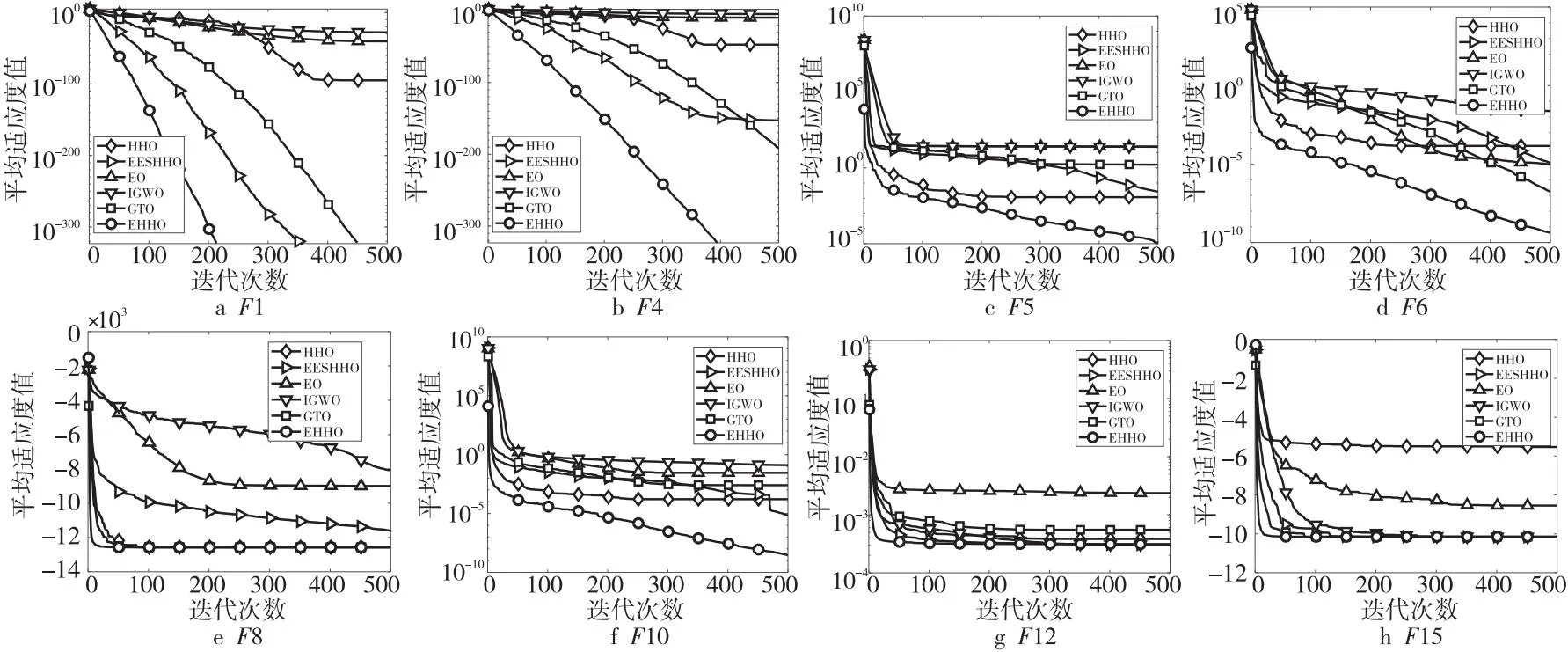
4.4 Wilcoxon秩和检验
4.5 高维情形下性能分析
5 结束语
