面向数据传输稳定性的无人机群频谱接入方法*

吴义政,杜奕航,张 余,钱鹏智

(1.南京信息工程大学 电子与信息工程学院,南京 210044;2.国防科技大学第六十三研究所,南京 210007)

0 引 言

近年来,无人机因其高机动性、低成本等特性引起了业界的高度关注,在侦察监视、辅助通信和信息采集等军事和民用领域得到了广泛应用[1]。随着无线通信技术的蓬勃发展,人们对信息传输速率的需求越来越高,用频设备呈爆炸式增长,可用频谱资源愈发稀缺且呈动态时变特性,因此,如何有效缓解频谱冲突、实现无人机群高效用频是当前面临的关键问题[2-3]。

由于无人机群所处空间位置以及网络拓扑结构动态变化,无人机群内部信息传输信道特性也呈现动态时变特性,然而传统方法中通常考虑准静态的互扰信道[4-5]。为快速高效实现无人机群内部用频协同,大多数研究都采用集中式网络架构或通过建立公共控制信道进行信息交互,在一定程度上能够减少无人机群内部用频冲突。如文献[6]通过集中控制器对用户频谱接入与切换实现统一管控,研究了数据猝发和用户移动条件下的传输队列稳定性问题,提出了一种联合信道分配和功率控制的策略,使得系统具有较好的鲁棒性。但该策略没有考虑高动态变化的无线环境,也未考虑集中控制带来的信令开销。为了克服集中控制存在的不足和其控制信道带来的频谱开销,文献[7]研究了时变频谱环境中面向干扰抑制的分布式信道选择问题,提出了一种完全分布式的非耦合随机学习算法。该方法虽然可以在时变无线环境下有效减轻用户间互扰,但并未考虑用户用频需求变化以及网络拓扑时变带来的影响,同时,该算法收敛速度也较慢。文献[8-10]研究了在无线环境变化缓慢情况下,采用深度强化学习方法来解决用户间的互扰问题。在用户数量和可用信道数量较少的情况下,所提算法能有效抑制用户间用频冲突,但是在用户数和信道较多情况下,用户间用频冲突缓解效果不佳。文献[11]针对信道分配问题给出了基于多臂赌博机的解决方案,但是不适用于业务数据猝发、无人机快速移动和无线通信等捷变的场景。

现实应用中无人机群主要面临以下问题:无人机群空间位置和网络拓扑结构动态变化,无人机所处无线通信环境具有时变性;无人机群频谱资源受限对通信开销较为敏感,在捷变频谱环境下建立公共控制信道十分困难;受限于无人机数据采集速率的波动性,集群中不同用户的用频需求实时变化。为此,本文针对时变频谱环境中无人机业务数据猝发情况下数据稳定传输问题,建立无人机业务数据包生成和实时向基站传输的模型,提出基于多用户非耦合排队的频谱接入方法。该方法为一种分布式方法,在必要的时候利用自身感知能力检测获得空闲信道,分布式无人机间无需任何信息交互,每架无人机仅根据其内外部状态和历史信息构建信道接入控制函数,并结合其已知信息生成用频决策。在保证网络中无人机业务数据队列稳定在一定范围的前提下,所提方法能有效缓解无人机用频冲突,提升信道利用率和系统吞吐量。

1 系统模型与问题构建

1.1 系统模型

考虑一个由多个无人机组成的分布式无人机群通信网络为地面用户提供中继服务(或者收集地面目标相关信息),并向基站实时传输到达的数据,如图1所示。该网络包含1个基站和N架无人机,无人机群集合表示为N={1,…,i,…,N},基站用符号o表示,无人机网络包含M个可用信道,其集合表示为M={1,…,m,…,M},且N>M,即无人机数量比信道数大,频谱资源不足。假设每个信道带宽都为B,无人机群飞行高度均为h,是个固定值。本文只考虑无人机向基站传输业务数据的下行链路。假设无人机移动区域为同一高度的二维有限平面区域,其被划分为多个等面积的方形栅格;基站位于地平面,高度为0,位置固定不变。为便于模拟无人机随机移动过程,假设所有无人机移动都是独立的且在每个时隙内只能在某个网格点上,下个时隙无人机将选择继续停留在原网格点或移动到某个相邻网格点。假设无人机独立执行任务,无人机生成的或到达的(后续仅称“到达”)业务数据和向基站传输的数据量用单位数据包来衡量。

图1 系统模型

无人机向基站传输数据时,假设所有信道都经历块衰落,即信道增益在同一时隙中相同,在不同时隙间随机变化,则时隙n内无人机i与基站间数据传输链路的瞬时增益为

(1)

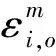
(2)

式中:pi(n)表示无人机i在时隙n内的发射功率。如果两架无人机在同一时隙内选择同一信道,它们之间将会发生用频冲突,则无人机i受到的互扰信号强度Ii和传输速率Ri分别表示为

(3)

(4)

式(3)中:Si(ai(n))={j∈N*i|aj(n)=ai(n)}表示在时隙n内,除无人机i以外所有使用信道ai(n)的无人机集合,N*i表示无人机集合N*中除去无人机i后的无人机集合;ai(n)表示无人机i在时隙n内选择的信道,ai(n)∈M*;σ2为噪声功率。设定每架无人机都有一个长度不受限制的业务数据传输队列,用于存储无人机到达的业务数据。对于任意时隙n≥0,无人机i的队列积压在前后两个时隙的关系可表示为

Oi(n+1)=max{Oi(n)-bi(n)νi(n),0}+Ai(n)

s.t.bi(n)∈{0,1}

(5)

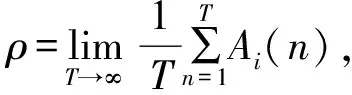
1.2 问题构建

无人机频谱分配与接入首要解决的是减少或消除无人机间用频冲突,以及提高信道利用率。在此借鉴文献[8]的思想,将前n个时隙无人机间用频冲突率(简称为“用频冲突率”)K(n)定义为

(6)

式中:c1(n)为时隙n时与其他无人机发生冲突的无人机总数量;N为总无人机数量。将前n个时隙内信道利用率L(n)定义为

(7)

式中:c2(n)为时隙n时被有效利用的信道数量,M为可用信道总数量;对于∀m(m∈M*),定义当且仅当有一架无人机在使用信道m,称信道m被有效利用。

此外,我们总是希望能够在单位时间内传输更多的业务数据,因此,在确保所有无人机业务数据传输稳定情况下,应最大化系统的最大稳定平均数据到达速率ρmax,可表示为ρmax=max {ρ|对于∀i∈N*,Oi(n)保持稳定}。

综上分析,本文的目标是找到一个均衡策略γ,可以最小化无人机间用频冲突率、信道利用率和最大平均稳定到达速率ρmax,即有

(8)

(9)

(10)

式中:C|D表示满足条件D的集合C。由式(8)～(10)可见,不仅要考虑系统无人机群用频冲突和信道利用率,还要考虑到无人机数据积压变化。

2 无人机频谱接入策略设计

2.1 频谱接入策略

无人机i在时隙n的信道使用状态定义为STAi(n),STAi(n)=0表示在时隙n内没有信道传输无人机i数据积压中的数据;STAi(n)=1表示在时隙n内有信道传输无人机i数据积压中的数据,且没有受到其他无人机的干扰;STAi(n)=2表示在时隙n内有信道传输无人机i数据积压数据,且遭受其他无人机的干扰。

当无人机使用信道传输其数据积压中的数据时,通过能量检测方法可以判断出其是否遭受其他无人机的干扰。

在确保所有无人机的业务数据队列积压保持稳定的前提下,无人机处于不同状态时其频谱接入策略不同,分为以下3种情况:

1)当STAi(n)=0时,为传输队列积压的数据,无人机需寻找空信道接入;为缓解无信息交互下无人机间存在的用频冲突,无人机i在0状态下保持1个时隙,其信道接入控制参数的更新为zi(n+1)=zi(n)+1,无人机在0状态下至少保持N-M个时隙数,即满足zi(n)≥N-M,无人机才能接入可用空信道,其接入所有可用空信道概率都相同。此时无人机i下一个时隙时接入信道r(r∈M)的概率为

当zi(n)>N-M,

(11)

当zi(n)≤N-M,

(12)

式(1)中:Y(n)={1,…,y,…,Y(n)}为在时隙n时可接入的空闲信道集合向量,Y(n)为在时隙n内空闲信道数;qi,r(n)表示无人机i在时隙n接入信道r的概率;qi,0(n)表示无人机i在时隙n不接入任何信道的概率;EF表示所有属于E且不属于F的元素。

2)当STAi(n)=1时,若无人机i使用信道m,为了避免其长时间占用信道资源,造成其他无人机无法有效使用信道,当其数据积压量小于一定值Δ时,在下一个时隙,无人机i将释放所占用信道,以供STAj(n)=0且参数zj(n)≥N-M的无人机使用,j∈N*,并且无人机i在下一个时隙的信道使用状态变为0;当其数据积压量大于Δ时,无人机继续保持原有的状态。无论无人机在上一个时隙的信道使用状态如何,无人机已经达到了单独占用信道的目标,则在下个时隙内其信道接入参数zi(n+1)=0。此时无人机i下一个时隙接入信道r的概率为

当Oi(n)>Δ,

(13)

当Oi(n)<Δ,

(14)

式中:Δ为无人机i释放占用信道的阈值,用于控制无人机释放或继续占用信道,以确保所有无人机的利益。

3)当STAi(n)=2时,若无人机接入信道m,为避免下个时隙无人机间继续在信道m发生互扰,也为了避免在其他信道上与其他无人机发生用频冲突,该无人机将依概率退出或留在原信道。在当前时隙中,无人机i因受到来自其他无人机的干扰无法有效利用信道进行数据传输,在下个时隙可能退出原信道,为了减少其影响,不改变信道接入控制参数,即zi(n+1)=zi(n),从而避免重新排队,有效地避免了其数据积压量大量增长。借鉴文献[12]的思想和方法,无人机i在下一个时隙接入信道r的概率为

(15)

式中:pi,r(n)和Ii(n)分别为时隙n内在信道r内基站接收到无人机i的信号强度和接收无人机i的信号受到的互扰信号强度;σ2为噪声功率。

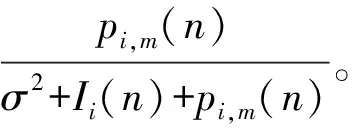
根据以上分析可以得到无人机i的信道接入控制参数zi(n)与历史信道使用状态的对应关系,如表1所示。

表1 无人机i的信道接入控制参数zi(n)与历史信道使用状态的对应关系表

从表1可以看出,无人机i在时隙n时可以根据当前时隙的信道接入控制参数zi(n)和上一个时隙的信道接入控制参数zi(n-1)得出下一个时隙的信道接入控制参数zi(n+1)。

2.2 频谱接入算法

为解决以上无人机群频谱接入问题,本文提出了基于多用户非耦合排队频谱接入算法。在时隙n内,无人机i根据生成的qi(n)选择信道接入(qi(n)为无人机i在时隙n接入M*中所有信道的概率集合,qi(n)={qi,r(n)}r∈M*)。无人机选择信道接入后根据2.1节给出无人机i在时隙n和n-1的信道使用状态,并根据表1的信道接入控制参数zi(n+1),如果STAi(n)=0且zi(n+1)>5,则采用能量检测方法获得所有空闲信道集Y(n);无人机根据其在时隙n+1内数据积压Oi(n+1)以及时隙n内信道使用状态STAi(n)、空闲信道集Y(n)和信道接入控制参数zi(n),利用公式(12)、(14)和(15)计算得出其信道接入概率向量qi(n+1)。

基于多用户非耦合排队频谱接入算法具体表述如下:

对于任∀无人机i∈N*,其传输诉求均为保障其队列中数据积压处于稳定状态,为了满足所有无人机的诉求,并行执行下列操作:

1 输入:无人机数量N、信道数量M、信道带宽B、飞行高度h、无人机发射功率pi

2 初始化信道接入控制参数、信道使用状态和信道接入概率等参数,zi(0)=0,STAi(0)=0

qi,r(n+1)=1/N,r∈M*

qi,r(n+1)=(N-M)/N,r=0

3 计算更新信道接入概率qi(n)

forn=1,2…

3.1 无人机i根据其信道接入概率向量qi(n)选择信道接入;

3.2 无人机i根据信道使用情况确定其信道使用状态STAi(n)

3.3 if STAi(n)=0 andzi(n+1)>5:

采用能量检测法检测出所有空闲信道

else:

不检测

end

3.4 更新无人机在时隙n+1内数据积压Oi(n+1)

3.5 根据信道状态信息STAi(n-1)和STAi(n),并结合表1得出信道接入控制参数zi(n+1)

3.6 更新计算无人机在下一个时隙内信道接入概率集合

if STAi(n)=0

根据公式(11)或(12)计算qi(n+1)

elseif STAi(n)=1

根据公式(13)或(14)计算qi(n+1)

elseif STAi(n)=2

根据公式(15)计算qi(n+1)

3.7 存储无人机当前时隙获得的参数值,做为其后续时隙的历史参数数据

end

end

4 输出:{qi(n)}n∈[1,T]

根据算法步骤和复杂度计算方法[13]可知,所提算法的计算次数跟10M呈线性关系,即O(10M)。本文用于对比分析的随机频谱接入算法(Random Spectrum Access Algorithm,RSAA)是一种多个移动同时随机接入信道方法,其复杂度为O(2M);基于效用的分布式子信道分配算法(Utility-based Distributed Subchannel Allocation Algorithm,UDSA)[14]是一种通过对每个局中用户引入一个额外状态变量“情绪”来控制信道接入的算法,其复杂度为O(2M)。对比可知,本文提出的算法复杂度稍比现有算法高,但相对来说是可以接受的。

3 仿真结果与分析

为了验证所提方法的性能,以RSAA和UDSA作为比较对象。参照文献[6]和[7]仿真参数设置方法,设置无人机数量N=20,噪声功率σ2=-100 dBm,信道带宽B=3 MHz,Δ=2ρ,传播路径衰落系数α=2。无人机飞行高度均为h=50 m,运动范围为2 000 m×2 000 m,网格面积为2 m×2 m,基站位于平面中心的正下方、高度为0的位置;无人机发射功率均为pi=24.77 dBm;数据包大小为3×104b。

图2给出了无人机群业务数据传输处于临界稳定状态时其用频冲突率随着时间变化的曲线,可以看出无人机系统在不同算法下处于各自临界稳定状态时,所提算法相比于其他两种算法,其用频冲突率显著减小,并随着时间增加,其用频冲突率逐渐降低,最后稳定在3%左右。这是由于所提算法中无人机在状态0时接入空闲信道需通过排队接入,从而有效避免了由状态2变为状态1和由状态0变为状态1时多无人机同时随机接入同一信道而造成的冲突;另外,当信道m上有多架无人机同时接入时,产生冲突的无人机将按照一定概率选择退出或留在信道m,在一定程度上也有效避免了原信道继续发生冲突;无人机根据业务数据传输稳定性,按需频繁地交替使用信道时,有效避免了与其他无人机发生互扰。

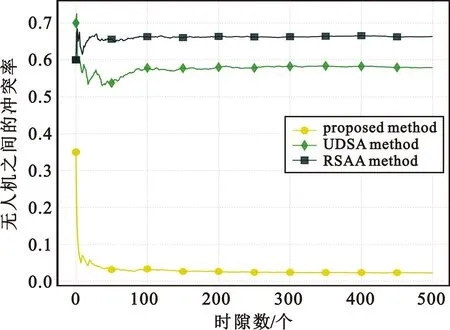
图2 无人机群业务数据传输处于临界稳定状态时其用频冲突率随着时间变化的曲线(M=15)

图3给出了无人机群业务数据传输处于临界稳定状态时其信道利用率随着时间变化的曲线,可以看出,所提方法中无人机群系统的信道利用率显著大于UDSA方法和RSAA方法。随着时间的增加,信道利用率逐渐增加,最后稳定在89%左右,这种变化趋势与图2相同。

图3 无人机群业务数据传输处于临界稳定状态时其信道利用率随着时间变化的曲线(M=15)

图4给出了不同ρ值下,无人机群平均数据积压量随时间变化的曲线。从仿真结果可以看出,在图4(a)、图4(b)、图4(c)中使用UDSA方法和RSAA方法时无人机的数据积压量变化过程都呈非线性增长,而在图4(d)中这一变化却呈线性关系。这是因为在平均数据到达率较低的情况下,UDSA方法和RSAA方法尚能在一定程度上完成积压数据的传输,因此其平均数据积压量呈现一定波动性;当平均到达率ρ达到33个数据包/时隙时,UDSA方法和RSAA方法在单位时间内传输的数据量相比于单位时间内到达的数据量和数据积压量,几乎可以忽略不记,因此使用上述两种方法时无人机的平均数据积压量几乎呈线性增长。与之形成鲜明对比的是,在不同数据达到率情况下,所提算法中无人机的平均数据积压量基本保持稳定,从而验证了在高业务负载情况下所提算法可以合理利用频谱资源有效完成数据传输。

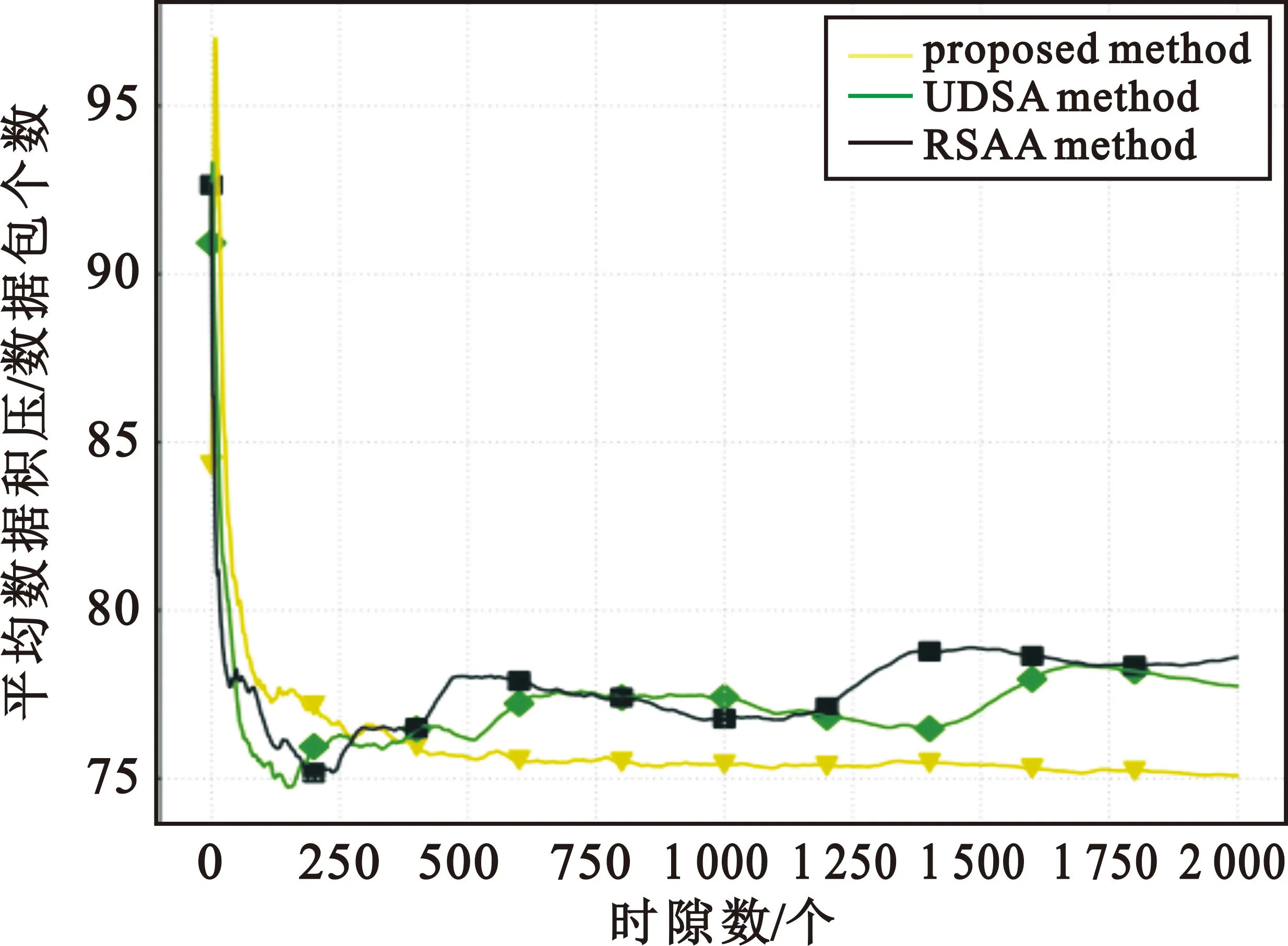
(a)ρ=9个数据包/时隙

图5给出了可用信道数量M不同情况下无人机群最大稳定平均到达速率ρmax的变化情况。从图中可以看出,3种方法中无人机群的ρmax值都随信道数量增加而提升,但所提算法中无人机群的ρmax值(或最大传输速率)相比UDSA提高了1.38～2.3倍,相比USAA算法提高了1.7～2.7倍,这是由于所提方法的信道利用率显著高于其他两种方法;此外,当无人机信道使用状态为1且其数据积压量小于阈值Δ时,无人机在下一个时隙将释放其占用的信道,从而避免了长时间占用有限的频谱资源,提升了系统吞吐量。

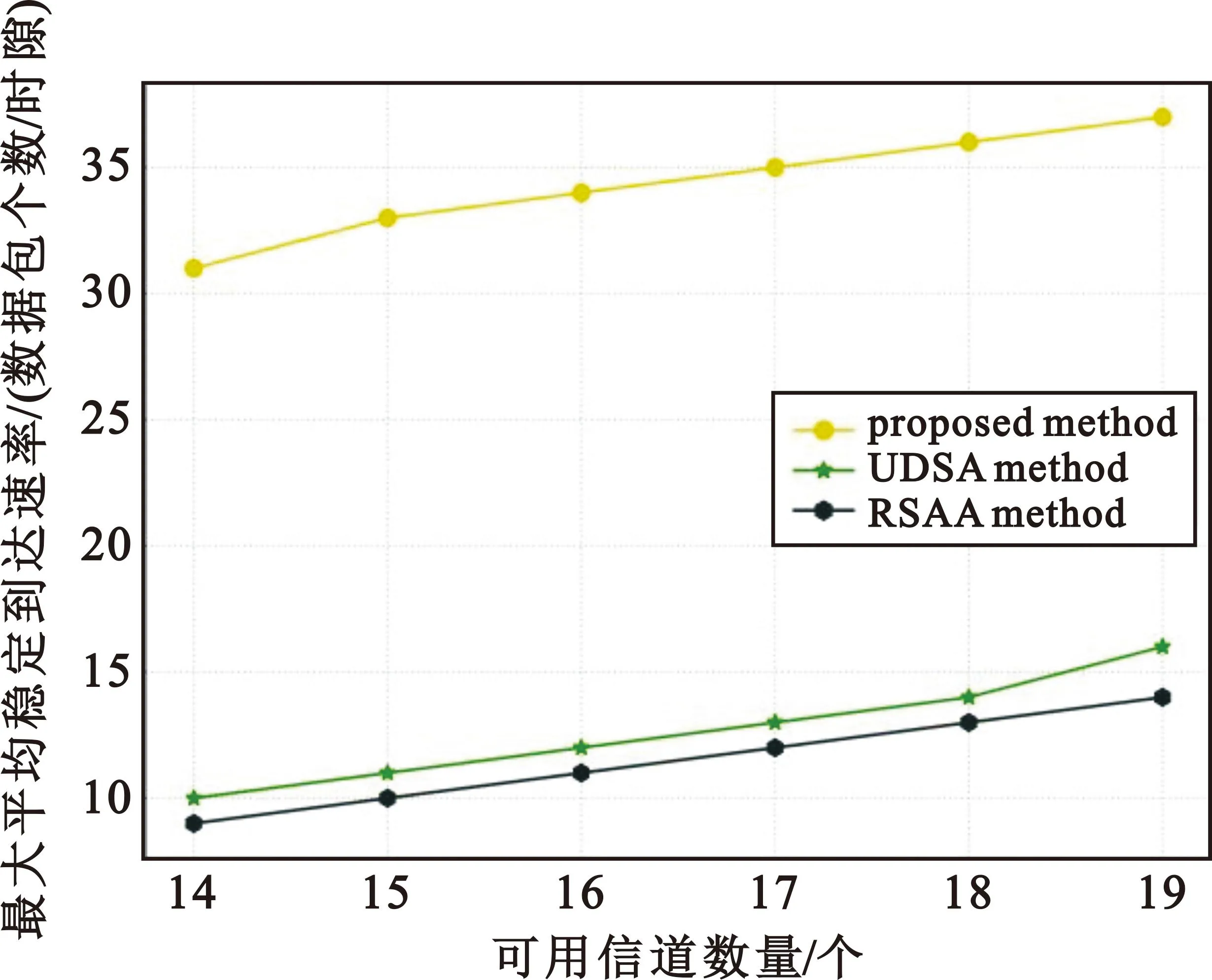
图5 无人机群最大平均稳定到达速率ρmax随可用信道数量M变化曲线

由于无人机数据积压与平均数据到达速率和传输速率相关,即数据积压一定时,无人机传输速率直接受平均数据到达率的影响,无人机传输速率伴随着平均数据到达率的提升而提升,从而使得无人机群吞吐量性能得到提升。

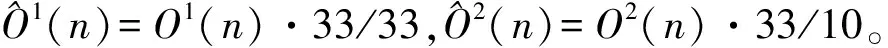
图6给出了可用信道数量M=15时无人机处于临界稳定状态时无人机最大数据积压差变化过程。从图6可以看出,相比其他两种算法,所提算法中无人机处于临界稳定状态时其最大数据积压差更小,其变化也较为稳定,有效确保了无人机间用频公平性。这是由于所提算法能使无人机按需接入信道,当无人机数据积压低于阈值Δ时,其将在下一个时隙自动释放所占用信道,以供其他无人机使用,有效地避免单个无人机长时间不能有效使用信道(信道使用状态不为1),从而使得最大无人机数据积压差得到有效控制;此外,当无人机由信道使用状态0变为信道使用状态2时,其在下一个时隙的信道使用状态变为2,其信道接入控制参数不变,避免了重新排队过程,从而在一定程度上避免了其数据积压量的增长。

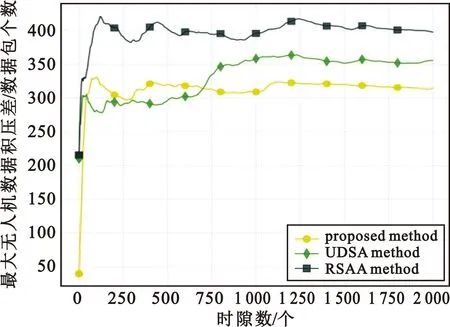
图6 无人机群处于临界稳定状态时其最大数据积压差变化曲线(M=15)

4 结 论

本文研究了在业务数据传输队列稳定前提下的无人机群频谱接入问题,以缓解无人机间用频冲突、提升信道有效利用率和系统吞吐量为目标,提出了基于多用户非耦合排队频谱接入方法。仿真结果表明,所提算法有效降低了无人机间用频冲突率、提升了信道利用率和系统吞吐量。此外,该算法适用于无人机内部和外部环境捷变的情况,如业务数据猝发、无线通信环境捷变等并存的场景。