基于任务生灭过程模型的边缘计算批处理调度算法分析与设计*
2024-02-28顾忆宵
罗 雨,顾忆宵,夏 斌
(上海交通大学 电子信息与电气工程学院,上海200240)
0 引 言
移动边缘计算技术(Mobile Edge Computing,MEC)在网络边缘接收处理用户卸载的计算任务,缓解核心网络拥堵的同时提高用户的体验特质(Quality of Experience,QoE)、降低计算任务的处理成本,在移动互联网时代得到快速发展。研究者们通过对增强现实[1]和在线游戏[2]等边缘计算场景下的计算任务展开内容相关性和请求动态特征的研究以降低资源开销、提高服务器工作效率。
文献[3-4]对任务相关性展开了研究、通过构建任务相关性感知的任务卸载机制以提高调度算法的性能表现,后者进一步引入了计算任务的迁移特征并建立马尔可夫决策过程(Markov Decision Process,MDP)。利用任务相关性建立同类任务并行计算的处理机制可以减少计算开销。文献[5-6]进一步从任务请求动态变化的角度出发进行讨论,前者将用户请求的到达情况建模为随机变量并基于排队模型进行优化研究,后者对车联网边缘计算场景下的计算任务随车辆运动的特征变化做出了讨论。任务动态变化特征可用于预测任务的未来变化趋势,辅助设计动态规划算法。
但上述研究忽略了计算任务的生灭特性,该特性在无线网络环境下广泛存在,如视频编码任务[7]、新移动应用计算任务[8]等。这一缺失降低了任务请求动态特征描述的准确性,同时使得动态规划算法难以突破当前的复杂度瓶颈得到进一步优化。基于此,本文综合考虑任务相关性感知和生灭动态特征构建MEC架构,利用相关性特征设计任务处理机制降低时延能耗成本,并在现有任务请求动态特征研究的基础上进一步将任务请求的到达情况建模为生灭过程。在使用贝尔曼方程求解无限期平均成本马尔可夫决策问题的过程中,通过提取任务请求的生灭特征对未来变化趋势作出判断,进而估计调度策略的时延能耗成本以辅助求得最优策略。这一优化定理对策略迭代操作进行状态空间和决策空间的剪枝以提高系统性能,基于此提出批处理调度算法。所提算法综合考虑任务的相关性和动态特征以取得性能优势,并通过基于生灭特征的剪枝方法突破了策略迭代的复杂度瓶颈。
1 系统模型
考虑一个离散时间多用户的MEC系统,网络中存在一个与云端服务器相连接的MEC服务器以及K个与MEC服务器相连接的独立用户,记作K={1,2,3,…,K},如图1所示。用户将请求卸载至接入点(Access Point),对应的边缘服务器将用户请求存储到队列中,运算完成后将结果传输给用户,超出边缘服务器承载能力的请求会卸载到云端服务器进行处理。

图1 基于任务相关性感知的MEC系统
1.1 任务模型
将服务时间以秒为单位划分为多个长度为τ的时隙,有索引t∈N+,用户在每个时隙随机向服务器卸载请求,考虑该边缘计算场景中有N种计算任务的请求,记作N={1,2,3,…,N}。将用户k∈K在t时隙卸载的属于任务类型n的请求的数量记作rn,k(t),所有用户卸载的属于任务类型n的请求总数记作an(t)≜∑k∈Krn,k(t),有r(t)≜{rn,k(t):n∈N,k∈K},a(t)≜{an(t):n∈N}。
计算任务的生灭变化建模如下:在任务类型n处于生状态时,这一类别的请求会在用户处产生并被卸载到MEC服务器;当任务类型n处于灭状态时,这一类别的请求不会被卸载到服务器。用b(t)≜{bn(t):n∈N}表示任务的生灭状态。当bn(t)=1,任务类型n在t时隙处于生状态。当bn(t)=0,任务类型n在t时隙处于灭状态。以VR场景为例,场景内事件的发生会带来一系列计算任务,这些计算任务随交互事件的出现消失而出现消失,交互事件出现时对应任务类型处于生状态,出现前或消失后处于灭状态。
(1)
式中:1(Ω)为指示函数,满足条件Ω时值为1,否则为0。时隙t新到的来自用户k的属于任务类别n的请求数量可以表示为rn,k(t)·bn(t)。
1.2 调度模型
t时隙MEC服务器队列中累积的同属于类别n的任务请求的数量记作qn(t)。在每个时隙开始时,服务器会选择一部分类别的任务请求来进行处理运算。用指示变量un(t)∈{0,1}来标记类别n的被选情况:当un(t)=1时,类别n的请求将会在t时隙进行处理,并在下一时隙将结果传输给用户,否则un(t)=0。相应地,把t时隙的调度决策记作u(t)≜{un(t)|n∈N}∈U,决策空间大小为|U|。将t时隙决定进行处理的任务请求类别集合记作N(t)={n|un(t)=1,n∈N}或Nu,类别数目记作m(t)=∑n∈Nun(t)。
如果决定对类别n的任务请求进行处理,则会将MEC服务器队列中累积的所有该类别的请求一并处理,同时清空请求队列qn(t)。因此,由用户k卸载的属于类别n的请求队列动态变化情况表示如下:
qn,k(t+1)=
min{1(un(t)≠1)qn,k(t)+rn,k(t)·bn(t),qmax}
(2)
式中:qmax是单个用户卸载的单类任务请求在服务器处的最大存储数量。在此基础上将类别n的任务请求积累数量记作qn(t)=∑n∈Nqn,k(t),对于时延容忍度为Tn的任务类别n,对应的t时隙的时延成本可以记作Dn(t)=qn(t)·Tn。同时整个系统在t时隙的总时延成本为
(3)
超出服务器存储能力qmax的请求需要迁移到云端服务器进行处理[10],将其产生的额外时延成本记作迁移成本:
Ln,k(t)=max(1(un(t)≠n)qn,k(t)+
rn,k(t)·bn(t)-qmax)·Tn,0}
(4)
有
(5)
1.3 计算模型
类别n的任务请求相关参数可以表示为In,On,Cn,Tn,In(单位:b),On(单位:b),Cn(单位:每比特所需CPU周期)分别代表该类任务请求的输入数据量、输出数据量、每比特数据计算所需CPU周期数。
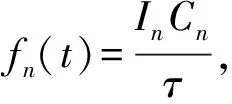
(6)
进而得到整个系统在t时隙的总计算能耗为
(7)
式中:κ为有效开关电容[13]。考虑到MEC服务器处的计算资源限制,同一时隙内最多可并行使用的虚拟机数量上限为mmax[14],因此一次调度决策中决定进行处理的任务种类数量存在上限m(t)≤mmax。
1.4 通信模型
着眼于通信资源受限的计算结果下行传输部分[15]。下行无线信道建模为块衰落的有限状态马尔可夫信道[16],将t时隙内用户k与接入点之间的信道增益记作hk(t),对应的可达速率(单位:b/s)为
(8)
式中:Pn,k(t),B,N0分别为传输功率、可用带宽以及复白高斯信道噪声的方差。为了在长度为τ的一个时隙内完成对数据量为On的计算结果的传输,传输速率必须达到On/τ。传输功率会受到用户中信道状态最差者的限制,即hn(t)≜mink∈Kn(t)hk(t),∀n∈N,其中Kn(t)≜{k|qn,k(t)>0,k∈K}。考虑以上因素,系统在t时隙进行任务类别n的计算结果的传输能耗表示如下:
(9)

(10)
2 问题建模与最优性分析
本节将基于上述MEC模型建立起优化问题并说明所采用的研究方法。首先基于贝尔曼方程对马尔可夫决策过程的值函数进行单调性分析,之后根据任务请求队列和生灭状态特征以及问题结构提出数条优化命题。
2.1 问题建模
t时隙开始时,MEC服务器需要根据系统状态S(t)≜{q(t),b(t)}∈S来确定调度决策u(t),将这一过程中使用的控制策略μ定义为由系统状态到调度决策的映射关系μ:{q,b}→u,函数表示为μ(q,b)=u。在后续的讨论中,前述时延、能耗成本可以表示为系统状态{q,b}和调度决策u的函数:时延成本表示为D(q),计算能耗成本表示为E1(u),通信能耗成本表示为E2(q,u),迁移成本表示为L(q,u)。
引入加权和方法对各项成本进行统筹优化,该MEC系统的一步加权成本可以表示如下:
g(q,u)≜D(q)+ω1E1(u)+ω2E2(q,u)+ω3L(q,u)
(11)
式中:ω1,ω2,ω3分别为计算能耗成本、通信能耗成本、迁移成本的权重参数。给定稳定的单链控制策略μ,系统的长期平均成本可以表示如下:
(12)
问题1 长期系统成本最小化问题:
(13)
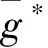
2.2 问题讨论
值迭代(Value Iteration,VI)和策略迭代(Policy Iteration,PI)都是解决MDP问题的常用方法。考虑到本研究中优化问题核心在于找到最优策略,同时策略迭代在许多情况下的性能表现优于值迭代[17],因此将策略迭代的方法作为研究的中心,并以此为基础进行优化理论的设计。
问题1是一个单链无限期平均成本马尔可夫决策问题,状态空间和决策空间有限,存在最优的确定性平稳策略,可以通过如下贝尔曼方程求得:
(14)
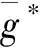
(15)
引入状态-决策成本函数J(q,b,u)≜g(q,u)+E(V(q′,b′)),代入式(15)可得
(16)
2.3 最优性分析
以模型中请求队列和生灭状态动态变化的特征为基础,结合值迭代的方法,分析得到值函数V(S)的如下性质:
引理1 值函数的单调性:对于任意一组系统状态S1=(q1,b1),S2=(q2,b2)∈S满足S1≤S2,有V(S1)≤V(S2)。
因篇幅所限,引理1的证明请用微信扫描本文OSID码,在“开放科学数据与内容”中查看。
以引理1为基础,结合问题的结构特征,可以得到关于J(q,b,u)的如下性质:
命题1 状态-决策成本函数关于请求队列状态的单调性:对于任意调度决策u,v∈U,有
J((q+en,k,b),u)-J((q+en,k,b),v)≤
J((q,b),u)-J((q,b),v)
(17)
式中:eu,k为一个N×K矢量(n∈Nu,k∈K),只有在(n,k)这一处的值为1,其他都为0。
命题的证明与文献[18]引理3类似。
命题1说明,对于系统状态{q,b}和调度决策u,v,如果状态-决策成本函数满足J((q,b),u)≤J((q,b),v),则对于衍生状态(q+en,k,b),决策之间的优劣关系仍然成立,有J((q+en,k,b),u)-J((q+en,k,b),v)≤0。派生状态与原状态的生灭特征相同,队列状态的差别满足命题1。由命题1出发,可以得到如下定理:
定理1 最优策略的最优性继承:使用策略迭代算法寻找最优策略μ*的过程中,如果式(18a)和(18b)条件成立,u=μ*(q2,b),则有μ*(q1,b)=μ*(q2,b)。
(18a)
(18b)
定理1表明,在策略改进步骤中计算状态{q1,b}所对应的最优调度决策时,如果已经求得状态{q2,b}的最优调度决策,同时这两个状态满足命题1所述关系,则状态{q2,b}的最优决策同时也是状态{q1,b}的最优决策。定理1的方法对策略改进过程中所需要遍历的状态空间进行剪枝以降低计算复杂度。
基于引理1和J(q,b,u)的性质,另有如下命题:
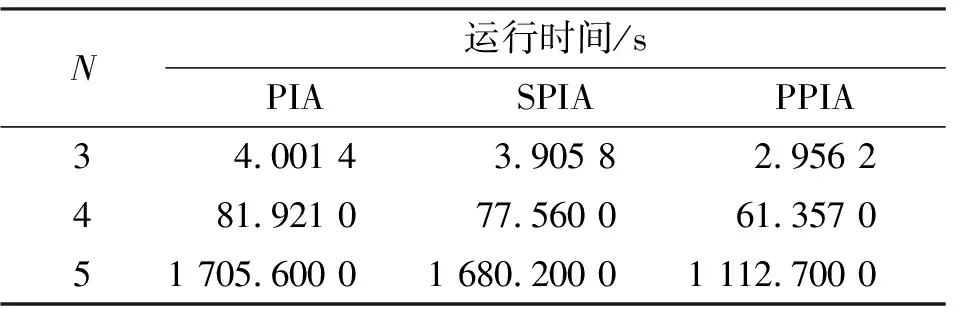
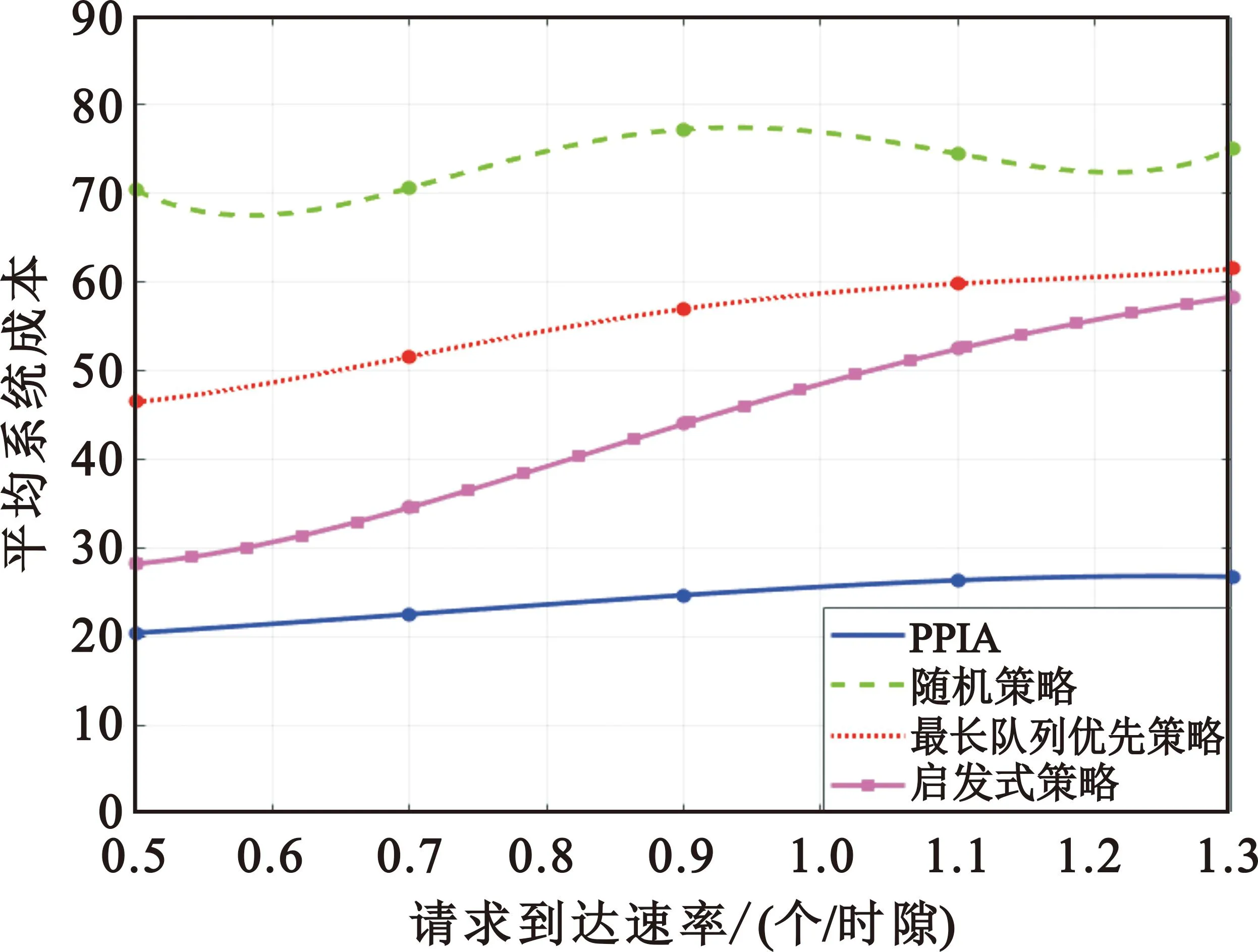
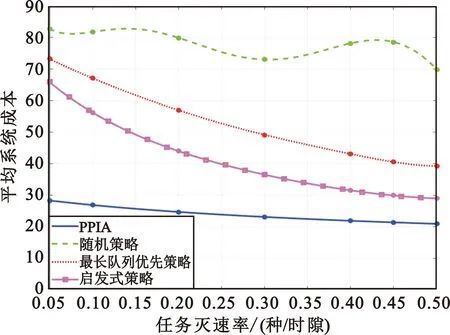
命题2 决策关于生灭状态的最优性:对于系统状态{q,b}和调度决策u=μ(q,b)∈U,其中满足∃n∈N,bn=0,qn>0,un=0,m=∑n∈Nun (19) σ=∑(q0,b0)∈S0Pr((q0,b0)|(q,b),μ(q,b)) (20a) S0={(q0,b0)|Pr((q0,b0)|(q,b) (20b) u0=μ(q0,b0) (20c) 因篇幅所限,命题的证明请用微信扫描本文OSID码,在“开放科学数据与内容”中查看。 命题2表明,给定控制策略μ,如果有一组系统状态{q,b}与对应的调度决策u=μ(q,b)满足命题2所述条件,则控制策略μ不是最优策略,且最优策略μ*严格优于μ。由命题2出发,可以得到如下定理: 定理2 最优策略的决策剪枝:求解最优控制策略μ*下状态{q,b}的最优调度决策μ*((q,b))时,如果状态{q,b}与对应的调度决策u满足∃n∈N,bn=0,qn>0,un=0,m=∑n∈Nun (21) 定理2表明,在遍历所有策略寻找状态{q,b}的最优策略的策略改进过程中,对于满足定理2的策略,应当直接予以排除,不需要迭代计算其值函数。由此实现对决策空间的剪枝,计算复杂度降低。 将定理1、定理2的策略与标准的策略迭代算法(Policy Iteration Algorithm,PIA)相结合得到低复杂度的最优算法,称为剪枝策略迭代算法(Pruned Policy Iteration Algorithm,PPIA)。相较于标准的PIA,PPIA利用定理1和定理2对策略改进步骤中需要遍历的状态空间和决策空间进行剪枝。剪枝策略迭代算法伪代码如下: 输入:系统参数,状态空间S,决策空间U,转移概率矩阵∑S′∈SPr[S′|S,u],一步成本g(q,u),初始控制策略μ,θ 输出:最优控制策略μ* 1 初始化所有状态S∈S的值函数V(S)=0 2δ=θ 3 whileδ≥θdo: 4 forS∈S do: 5v←V(S) 6V(S)←g(S,μ(S))+∑S′∈SPr[S′|S,μ(S)](V(S′)) 7δ←max {δ,|v-V(S)|} 8 end 9 end 10 PolicyStable←true 11 forS∈S do: 12 OldAction←μ(S) 13 if存在已遍历的状态S′满足定理1 then: 14μ(S)=μ(S′) 15 else ifS满足定理2 then: 17 foru∈Udo: 18 Ifu满足定理2 then: 20 end 22 else 24 end 25 If OldAction≠μ(S) then 26 PolicyStable←false 27 end 28 if PolicyStable then 返回μ*=μ 29 else回到第3行 算法第2~9行是策略验证步骤,第10~29行是策略改进步骤。 从第11行开始以逆字典序遍历状态空间,在第13行对满足定理1的状态S进行剪枝:如果其衍生状态S′在本次策略改进步骤中已经被遍历,则依照定理1将μ(S′)直接作为μ(S)的解,不再需要迭代求解,由此实现对状态空间的剪枝。 从第15行开始,遍历每个状态的决策空间以找寻最优决策,在此处引入定理2,对于满足定理2的状态-决策组合(State-action Combination)可以直接跳过不进行遍历,由此实现对决策空间的剪枝。 对于标准的PIA,需要遍历大小为|S|的状态空间和大小为|U|的决策空间来求得μ(S),每次迭代的总复杂度为O(|S|3+|U||S|2)。PPIA通过减少需要遍历的状态空间和决策空间大小,使得其计算复杂度低于PIA。由于采用了相同的迭代方法,PPIA的最优性和可收敛性与PIA一致[17]。 通信模型与计算模型相关参数配置情况如表1所示,有限状态马尔可夫信道的信道增益hk参考[19]进行配置。 表1 仿真参数配置 从算法运行速度和调度策略的平均成本这两方面来进行仿真设计。作为对照的算法包括标准的PIA算法[17]、同样基于动态规划但未考虑生灭特征的SPIA算法[18]、随机策略、最长队列优先策略[20],以及基于本研究场景提出的启发式策略。启发式策略以队列负荷为标杆,优先处理灭状态、队列负荷较高的任务请求。 本小节与其他最优算法的运行时间进行对比,运行时间越短说明算法复杂度更低、运行效率更高。为体现优化理论的剪枝性能,讨论能耗权重参数ω1和ω2的变化对不同算法运行时间的影响。实验结果如表2所示,PIA和SPIA的运行时间受权重参数变化的影响较小,PPIA的运行时间随能耗参数减小而减小。原因在于,定理2的剪枝优化性能受具体的权重参数影响,当能耗权重参数ω1和ω2增大时,状态空间和决策空间中满足定理2中不等式条件的状态与决策数量增加,可以剪枝处理掉的状态更多,算法复杂度和运行时间随之降低。PIA没有进行剪枝,SPIA没有针对生灭过程进行剪枝,因而运算时间长于PPIA。PPIA在ω1=0.4,ω2=0.4时将运行时间缩短至2.956 2 s,相较于PIA算法有高于26%的效率提升。 表2 系统的能耗权重参数ω1和ω2变化时不同算法所对应的运行时间差别 为体现PPIA能在更复杂场景下保持性能优势,讨论系统内任务请求种类数量的变化对不同算法运行时间的影响。实验结果如表3所示,随着请求种类数量的上升,系统复杂度与算法运行时间提高,使用剪枝优化的PPIA始终保持25%以上的运行时间优势。 表3 系统的任务请求种类数N变化时不同算法所对应的运行时间差别 综合以上两则实验场景可得,以定理2为基础的剪枝算法PPIA能在保持最优性的同时相较于PIA算法和SPIA算法有着更快的运行速度,在一定的能耗权重参数下表现更佳。 本小节与其他次优算法的平均成本进行对比。为体现PPIA在不同系统负载下的平均成本优势,比较平均请求到达速率变化对不同算法所对应的调度策略的平均成本的影响,实验结果如图2所示。随着请求到达速率的提升,更多的请求带来更多的时延、能耗成本,平均成本呈上升趋势,当到达速率大于1.1时趋于稳定,PPIA的调度方案平均成本由20.3839上升至26.740,保持最低的同时在到达速率较高时体现出明显优势。启发式算法在到达速率低于0.7时性能表现相对优秀,但当到达速率逐渐上升时与PPIA之间的差异明显增大。到达速率的提高带来了更高的队列负荷,需要消耗更多的能耗成本进行处理或在节省能耗成本的同时面对更高的时延和迁移成本,PPIA能准确权衡成本取舍,同时通过迭代寻求最优解,因而相较于其他次优算法表现良好。启发式算法能平衡队列负载,但当请求到达速率较高时需要更高的能耗成本以保持队列负载平衡,性能表现严重下降。 图2 系统的请求到达速率变化时不同算法所对应的平均成本差异 为体现PPIA在不同生灭场景下能保持性能稳定,比较任务死亡率变化对不同算法平均成本的影响,实验结果如图3所示。随着任务死亡率的上升,任务的平均激活周期变短,请求数量下降导致调度方案的平均成本下降,同时生灭频率的变化会让算法难以对请求的未来到达情况做出估计、降低算法性能的稳定性。在死亡率低于0.4、任务生周期较长时,最长队列优先策略和启发式策略难以在生状态判断是否应当积累请求等待后续处理,同时难以在灭状态判断是否应当等待下一次生状态再行处理,因此综合性能表现差。基于生灭过程开发的PPIA能在不同生灭速率下准确判断未来状态的请求到达期望以取得最优性能表现,平均成本保持在30以下。当死亡率较高时,启发式算法的平均成本变化趋于稳定,但仍然劣于PPIA。 图3 系统的任务死亡率变化时不同算法所对应的平均成本差别 综合以上两则实验场景可得,启发式算法和最长队列优先算法在低到达速率、低死亡率等场景下性能表现不佳,PPIA则能在不同系统条件下保持性能稳定,平均成本低于其他次优算法。 针对现有边缘计算研究未考虑任务生灭特征而存在复杂度瓶颈,本文提出基于生灭过程和任务相关性感知的边缘计算模型并给出剪枝策略迭代算法,利用任务的生灭特征对未来请求到达情况进行判断,辅助确定当前状态最优决策以降低迭代过程中遍历的状态空间和决策空间大小。仿真结果表明,基于生灭特征取得的优化定理使得所提算法突破了策略迭代的复杂度瓶颈,计算开销低于标准策略迭代算法,同时时延能耗成本低于最长队列优先策略等次优策略,且能在多变的系统状态下保持性能稳定。3 基于分析得到的最优算法
4 性能仿真与分析
4.1 仿真环境与设置

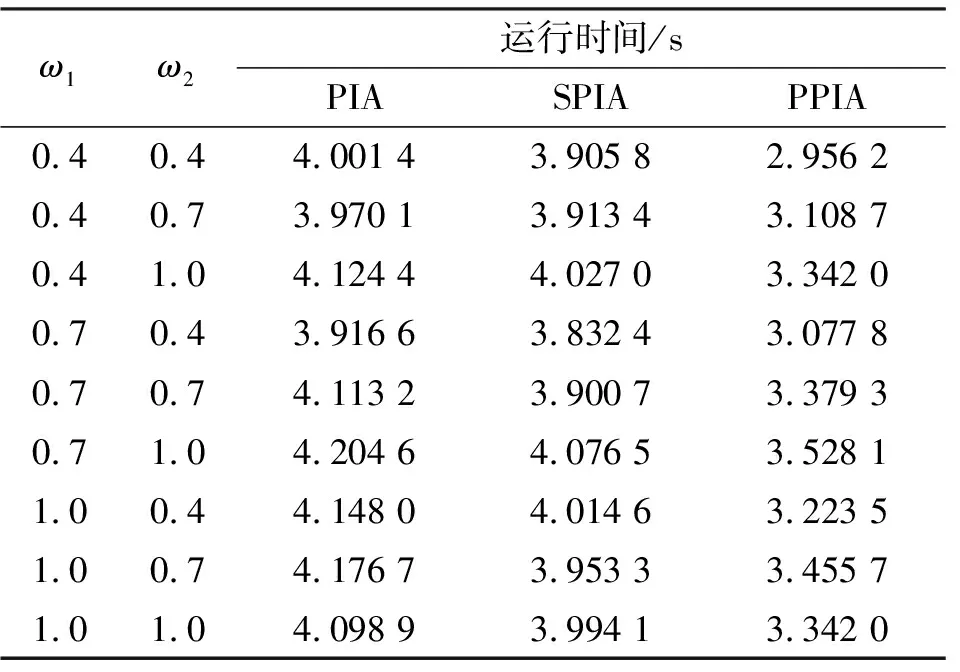
4.2 算法运行时间分析
4.3 算法平均成本分析
5 结 论
